多尺度河流和湖泊的矢量目标匹配方法研究

钟 东，郭庆胜，王 勇，刘纪平

(1.武汉大学 资源与环境科学学院，湖北 武汉 430070;2中国测绘科学研究院，北京 100830)

多尺度河流和湖泊的矢量目标匹配方法研究

钟 东1，郭庆胜1，王 勇2，刘纪平2

(1.武汉大学 资源与环境科学学院，湖北 武汉 430070;2中国测绘科学研究院，北京 100830)

研究河流和湖泊的矢量目标匹配方法在地理空间变化检测、地图更新等方面具有重要意义。文中提出一种计算线线部分匹配的折线集的算法，基于该算法和面面叠置率，研究河流和湖泊的面面、面线、线线1∶1匹配算法和非1∶1匹配策略，实现河流和湖泊整个目标数据集的匹配。实验表明，文中所研究的算法和策略具有两个优点：解决了面与线在不相交情况下的匹配问题；对数据误差有很强的适应性。

多尺度; 河流;湖泊;目标匹配

空间目标匹配可以为进一步探测不同数据集之间的差异或变化奠定基础[1]，河流和湖泊是两类重要的地物，研究河流和湖泊的多尺度矢量目标匹配技术在地图合并、地图更新、变化检测等方面有重要意义[1-2]。河流和湖泊空间目标匹配包括1∶1匹配和非1∶1匹配两大类。已有的面面1∶1匹配算法主要包括基于相似度匹配方法[2]、基于拓扑关系进行匹配的方法[3-4]、基于模糊拓扑关系分类进行匹配的方法[5-6]、基于概率的面目标匹配方法[7]、基于重叠度的面目标匹配方法[8-9]；已有的线线1∶1匹配算法主要有基于几何相似度的匹配方法[7, 10]、基于拓扑结构的匹配方法[11-12]、基于智能化方法的匹配方法[13-14]；而面线匹配主要通过提取面的骨架线与线目标进行匹配来完成[15-16]。现有算法难以解决面线不相交情况下的匹配，对数据误差的适应性差。本文提出利用线与线部分匹配的折线集，改进基于几何相似度的线线1∶1匹配算法，并将面线匹配转换成线线匹配，将面面、面线、线线1∶1匹配的结果应用于非1∶1匹配。

1 河流和湖泊目标匹配的特点

河流要素在几何上主要有以下3个特点：①河流多为狭长面目标；②同一地形图上，不同河流之间的宽度差异可能较大；③同一条河流的不同部分的宽度差异可能较大。相对于河流，湖泊的特点则表现为面积较大，部分湖泊有狭长支流。

一般情况下，目标匹配先基于语义挑选出同一类型的地物，然后再进行匹配。对河流和湖泊而言，大比例尺的河流只与小比例尺上的河流匹配，湖泊亦如此。但是当湖泊与河流相接时，湖泊的某一部分可能变为小比例尺的一小段单线河，此时可以考虑河流和湖泊的跨地物类型匹配。如图1所示，M0(粗实线)和N0(粗虚线)分别表示大比例尺上的湖泊和单线河，M1(细实线)和N1(细虚线)分别表示小比例尺上的河流和湖泊，C0和C1是N1上的两个点，阴影部分表示M0的一条细小支流。由于制图综合的影响，M0的细小支流在小比例尺上以单线河(折线段C0-C1)的形式呈现。于是，就存在湖泊M0(湖泊的部分)与河流N1(河流的部分)之间的匹配。值得注意的是，此处匹配只是建立目标M0，N0与目标M1，N1之间的关系，而各目标的语义并没有发生变化。

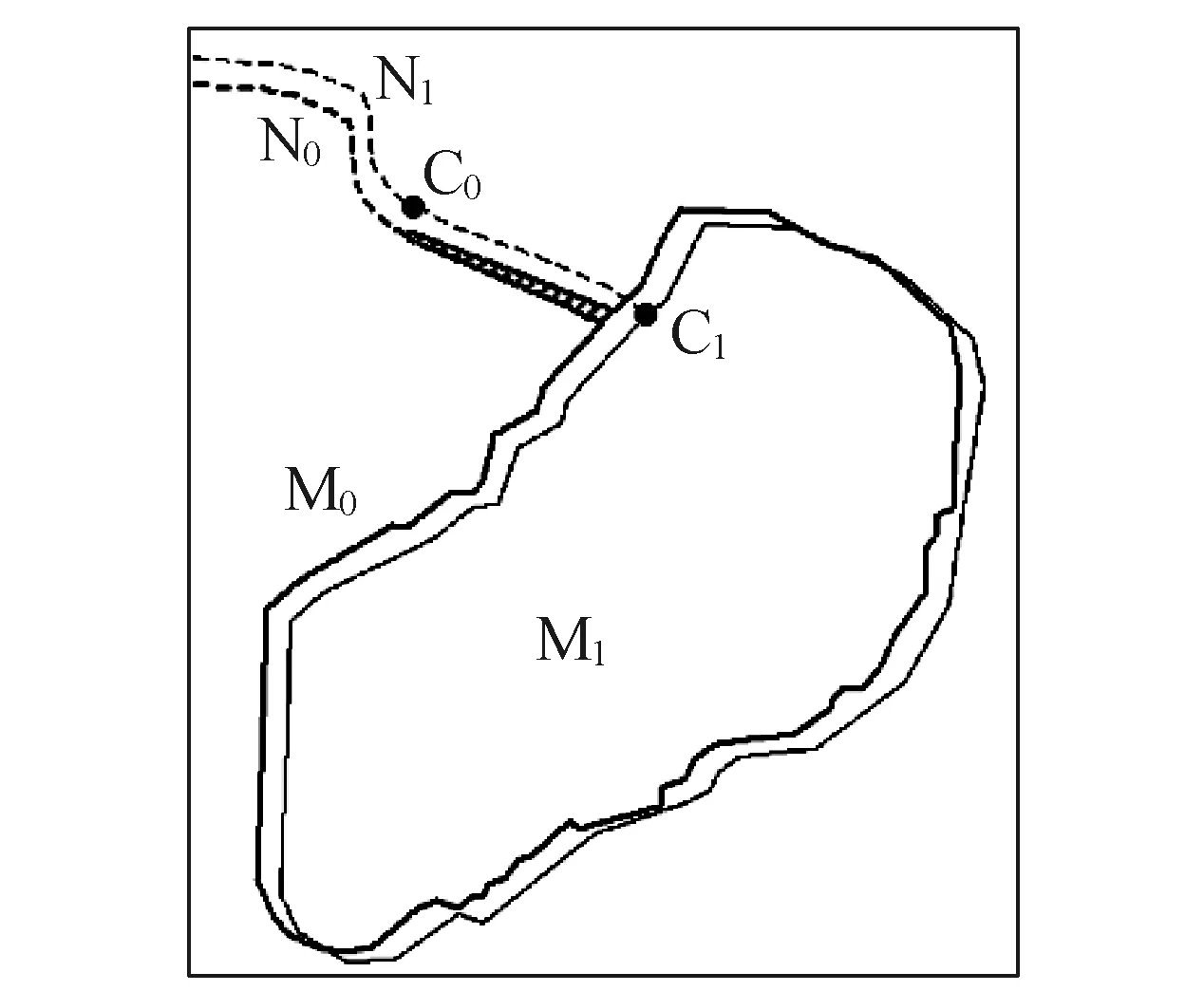
图1 河流和湖泊跨类型匹配

在参与匹配的数据源中，通常将现势性好、位置精度高的数据源称为参考数据源(通常为较大比例尺)，而将现势性较差、位置精度相对较低的数据源称为目标数据源(通常为较小比例尺)[2]。导致不同地图空间中的同名目标之间的差异的原因有很多，主要包括制图综合、实际变化和数据误差3种[15]。其中制图综合是导致同名目标发生变化的主要原因，根据综合算子不同又分为选取、简化(包括尺度变化)、多目标的合并、移位、夸大以及典型化。实际变化包括地物的出现、改变和消失。数据误差则体现在目标位置的改变。

目标选取和出现导致在小比例尺地图上没有与大比例尺地图上相对应的目标。目标消失则导致小比例尺地图上的目标在大比例尺地图上不显示。数据误差和移位导致目标的位置差异。简化、夸大会造成目标在空间形状、大小等表达上的差异，简化也可能导致目标尺度发生变化。合并、典型化则会造成目标在空间形状、大小和结构等多方面的差异，合并还可能导致目标的数量发生改变。

矢量数据的几何类型分为点、线、面，河流和湖泊匹配主要考虑面与线2种几何类型。由于河流和湖泊本身的特点以及尺度的变化，参考数据源和目标数据源中均可能出现面目标和线目标，则河流和湖泊的匹配类型(几何)就分为面面、面线、线线匹配3种几何类型组合。

文献[15]和[16]根据每轮匹配中参考数据源和目标数据源的目标数量之比分为1∶0、0∶1、1∶1、1∶M、N∶1、N∶M 6种匹配模式，本文提出的匹配模式与此相同，只是每轮匹配中参考数据源中的目标数量和目标数据源中的目标数量均有可能是面目标数量与线目标数量的总和。

因此，河流和湖泊的匹配类型可以归纳为未匹配、面面匹配、面线匹配、线线匹配4种，匹配模式可以归纳为未匹配(1∶0、0∶1)、1∶1匹配、非1∶1(1∶M、N∶1、N∶M)匹配3种。对于未匹配的情况，其实没有单独涉及到匹配算法，因此，本文只需考虑面面匹配、面线匹配、线线匹配3种匹配类型和1∶1、非1∶1两种匹配模式。

2 计算线线部分匹配的折线集

两条折线的匹配可以分为完全匹配和部分匹配。在部分匹配时，匹配成功的部分由一系列折线段组成，本文称这些折线段构成的集合为线线部分匹配的折线集。为了尽可能准确地计算能部分匹配的折线段，需要对线目标进行顶点加密。匹配的两条折线段的距离应该为零，方向应该一致，但由于地图数据误差的影响，距离和方向都存在一定的偏差。因此，在匹配时，需要指定距离阈值和方向阈值。一般情况下，视力正常的人的肉眼能分辨的图上最短距离是0.1 mm，距离阈值的设定也是为适应地图的误差，再根据3倍中误差原则，可得距离阈值的算式为

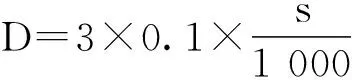
式中：s为地图比例尺分母；D表示实地距离，单位为m。

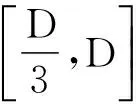
如图2，L1表示细实线，L2表示细虚线，顶点1到顶点8和顶点9到顶点16分别表示L1和L2顶点加密后的部分顶点。假设L1和L2加密后的顶点集分别为P1和P2，两个临时的顶点集合T1、T2，则计算L1与L2部分匹配的折线集的算法描述如下(见图2)：

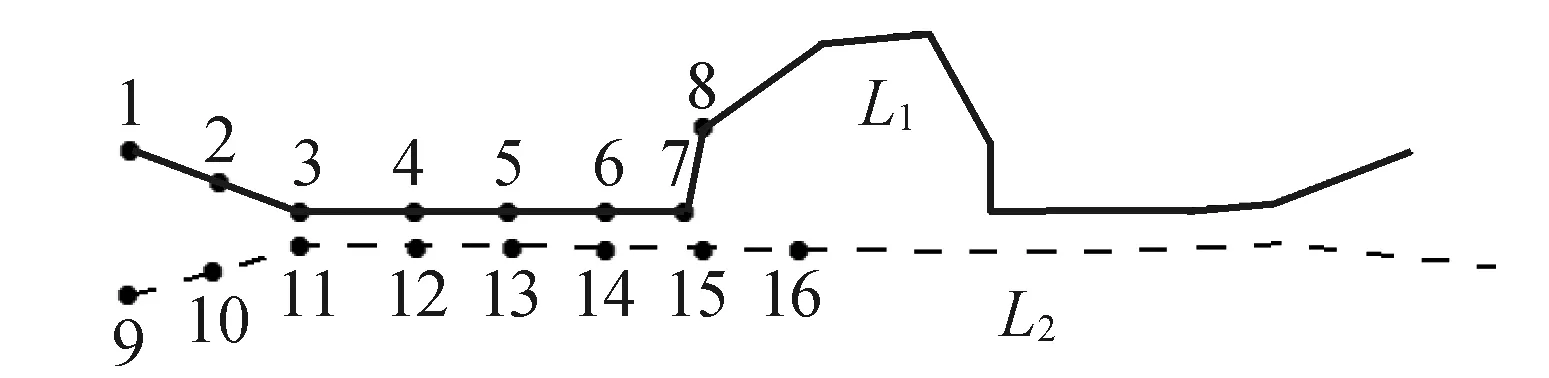
图2 计算线线部分匹配的折线集原理

1)遍历顶点集合P1，得到点1，在P2中找到点1的最近点(图1的点9)，由于点1和点9之间的距离大于D，继续遍历P1集合。清空T1和T2。

2)当遍历到点3时，在P2中找到点3的最近点(点11)，点3和点11之间的距离小于D，但由于T1和T2均为空，不能判断方向，直接将点3加入集合T1，点11加入集合T2。

3)当遍历到点4时，在P2中找到点4的最近点(点12)，点4和点12之间的距离小于D，此时T1和T2不为空，则计算线段(3-5)和线段(11-12)的方向β，由于β小于α，因此将点4加入集合T1，点12加入集合T2。

4)当遍历到点5时，在P2中找到点5的最近点(点13)，点5和点13之间的距离小于D，此时T1和T2不为空，则计算线段(4-5)和线段(12-13)的方向β，由于β小于α，因此将点5加入集合T1，点13加入集合T2。

5)继续遍历P1集合，当遍历到点8时，在P2中找到点8的最近点(点16)，点8和点16之间的距离大于D，因此，不能再向T1和T2中添加顶点8和16，此时的顶点集合T1和T2就构成两个折线段。存储T1、T2，再清空T1和T2继续遍历。

6)同理，可以按照步骤1)到步骤5)计算L1与L2部分匹配的其他折线段，所有的折线段构成的集合就是L1与L2部分匹配的折线集。

L1与L2部分匹配的折线集计算结果如图3所示。图中粗实线(折线段a，b，c，d)表示部分匹配的折线集，该折线集分为两部分：L1上的部分匹配的折线集({a，b})和L2上的部分匹配的折线集({c，d})。

图3 部分匹配的折线集计算结果

3 1∶1匹配算法和非1∶1匹配策略

目标A(面或线)与目标B(面或线)的1∶1匹配结果有5种(假设每种结果用一个整数表示)： ①A与B未匹配(用0表示)； ②A与B(完全)匹配(用1表示)； ③A部分匹配B，也就是A匹配B的一部分，(用2表示)； ④B部分匹配A，也就是B匹配A的一部分，(用3表示)； ⑤A部分匹配B，同时，B也部分匹配A，(用4表示)。

3.1 线线、面线1∶1匹配算法

假设L1与L2的部分匹配的折线集为R，其中L1上的部分匹配的折线集为R1，L2上的部分匹配的折线集为R2，则L1与L2部分匹配的长度ML1为R1所有折线段的长度和，L1与L2部分匹配的长度ML2为R1所有折线段的长度和，再假设L1的长度为Len1，L2的长度为Len2，则有L1与L2的相似度S1和L2与L1的相似度S2为

将计算改进的线线相似度的思想与文献[15]和[16]中的面线匹配算法进行融合，可以弥补现有面线1∶1匹配算法的缺陷。假设面目标P和线目标L进行1∶1匹配，P的骨架线集合为Ske，i表示Ske中第i个元素(i= 0, 1, …,n-1)，n为Ske集合的元素个数。先计算每条骨架线与L的部分匹配的折线集，从而得到Ske中第i条骨架线与L匹配的长度为SL1i，L与Ske中第i条骨架线匹配的长度为SL2i。再假设面P的所有骨架线的长度和为PL，线目标L的长度为LL，则得到P与L的相似度S1和L与P的相似度S2为

3.2 面面1∶1匹配算法

同一地区不同来源的地图(即使是不同比例尺)在消除整体和局部坐标偏差后，同名面实体总是会有较大的重叠面积；面实体之间的重叠面积大小反映两个面之间的距离差异以及形状差异等，而且它反映两个面实体之间的整体相似性，符合人眼的视觉效果[5]。因此,本文使用面面叠置率来计算面面1∶1匹配结果。在重叠面积的基础上，面积叠置率定义为两个面域重叠部分面积与各自总面积的比率[6]。假设面A1的面积为a1，面A2的面积为a2，A1与A2的重叠面积为a0，则A1与A2的叠置率O1和A2与A1的叠置率O2分别为

改革开放的总设计师邓小平同志曾说过：“科学技术是第一生产力”，目前通明公司虽然仍存在很多不尽如人意的地方，但是我相信，在单位领导的正确领导下，只要我们不断提高自身业务水平，培养并储备充足的技术人才，我们一定有足够的能力和社会上的路灯企业竞争，在日后的工程投标中胜出，成为市场经济大环境下的弄潮儿。

在进行面面、面线、线线1∶1匹配时，由于地图误差的存在，面、线目标的位置有误差，使得完全匹配的两个目标，其相似度S1，S2(叠置率O1，O2)不一定为1，因此，当S1，S2(叠置率O1，O2)均大于一定阈值Smax(Omax)，就可以认为这两个目标是完全匹配的。同理，由于地图误差的存在，如果两个目标的相似度S1，S2(叠置率O1，O2)均小于一定阈值Smin(Omin),则认为这两个目标不匹配。假设目标A(面或线)和目标B(面或线)的1∶1匹配结果用r表示，则A与B的1∶1匹配结果的判断规则如图4所示(以面线、线线为例，面面1∶1匹配结果的判断规则类似)。

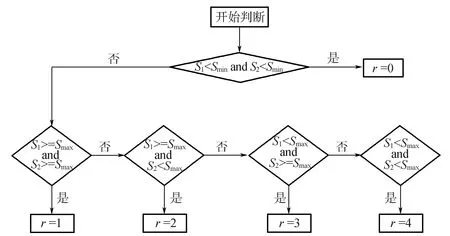
图4 1∶1匹配结果判断规则

3.3 非1∶1匹配策略

针对河流和湖泊的目标匹配，本文的策略是：使用面面、面线、线线1∶1匹配算法，计算两个目标的1∶1匹配结果，然后根据1∶1匹配结果进行非1∶1匹配。在进行河流和湖泊的目标匹配时，参与匹配的数据集有4个：参考数据源的面目标集DS1、线目标集DS2，目标数据源的面目标集DS3、线目标集DS4。大比例尺地图上的面目标在小比例尺地图上变成线目标是由尺度变化引起的，因此不考虑大比例尺地图上的线目标与小比例尺地图上的面目标进行匹配的情况，并且，参考数据集中的目标只能和目标数据集中的目标匹配。因此，数据集之间可能进行匹配的对应关系是：DS1与DS3、DS4，DS2与DS4，DS3与DS1，DS4与DS1、DS2。匹配时，遍历对应数据集中的目标，针对当前遍历得到的两个目标(假设为OB1和OB2)，根据其几何类型组合，选择使用面面、面线或线线1∶1匹配算法，计算其1∶1匹配结果r，根据r的值做如下处理：

1)若r=0，OB1与OB2不匹配，此时只需要继续遍历数据集中的下一个目标；

2)若r=1，OB1与OB2完全匹配，OB1与OB2均不需要再跟别的目标匹配；

3)若r=2，OB1部分匹配OB2，OB1不需要再跟别的目标匹配，而OB2需要再跟别的目标匹配；

5)若r=4，OB1部分匹配OB2，同时，OB2也部分匹配OB1，OB1与OB2均需要再跟别的目标匹配。

由于待匹配的河流和湖泊数据集庞大，在匹配的过程中使用了格网索引、MBR[15-16]等技术。格网索引可以有效缩小遍历范围，而在判断两个目标是否匹配时，要先判断这两个目标的MBR是否相交，如果相交则再使用相应的1∶1匹配算法，对于MBR不相交的目标则不需要计算其1∶1匹配结果，可有效减少计算时间。

4 实验与分析

为了验证本文所研究的算法和策略的正确性，用武汉市局部地区的水系数据进行实验。该实验的参考数据源为1∶50万，有115个面状目标(图5(a)实线)和24个线状目标(图5(a)虚线)；目标数据源为1∶400万，有43个面状目标(图5(b)实线)和46个线状目标(图5(b)虚线)。实验中，设置插点距离为100 m，距离阈值为150 m，方向阈值为0.5度，Smax和Omax都为0.9，Smin和Omin都为0.1。

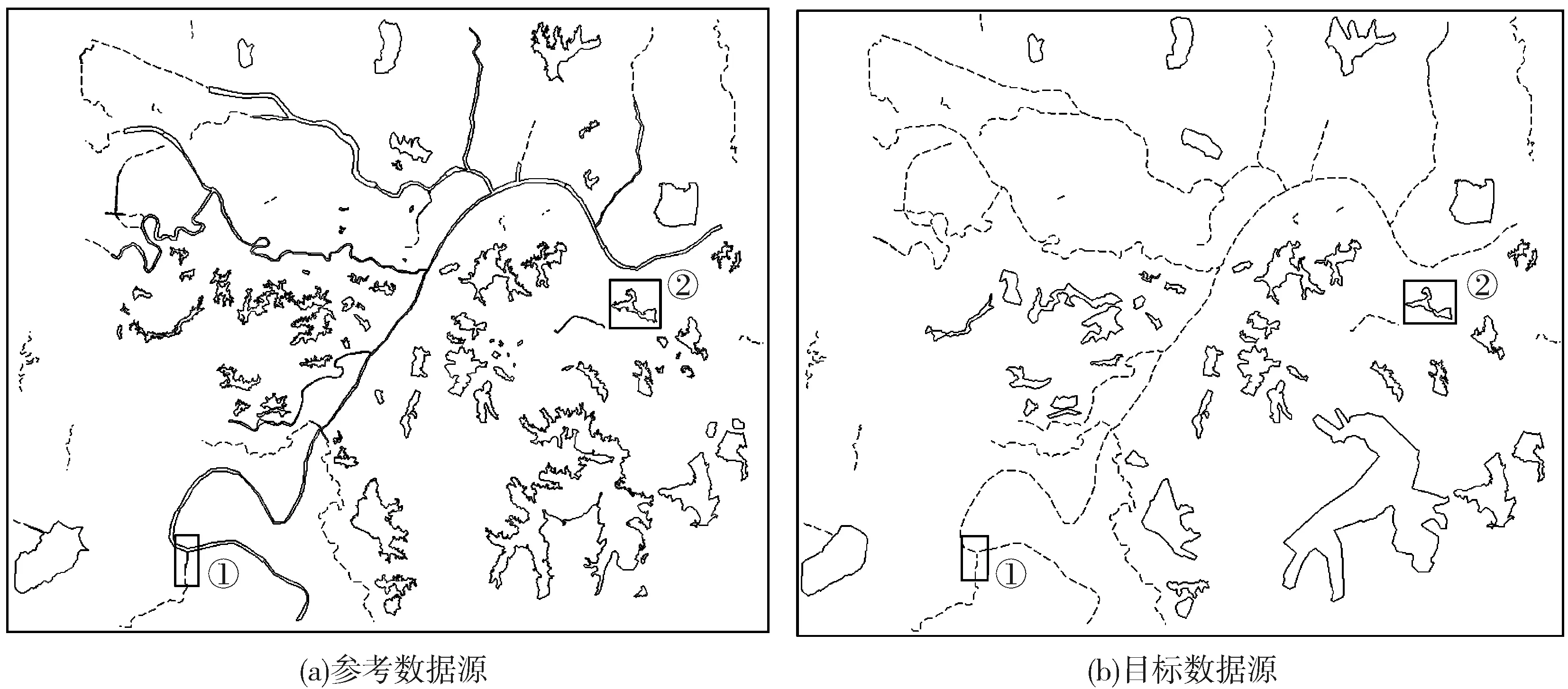
图5 实验数据

实验结果如表1所示，有49对目标匹配成功，15对目标未匹配。匹配成功目标的几何类型组合有面、线—面、线，面—面，面—线，线—线4种；未匹配的目标包括参考数据源中的12个面目标和目标数据源的3个线目标。图6(a)和图6(b)分别对应图5中①号方框和②号方框所在位置的数据的放大，图6(c)对应图6(b)中③号方框所在位置的数据的放大，这几个位置的数据比较典型。通过实验，本文所研究的算法和策略的优点得以证明：

表1 实验结果

1)面线不相交情况下依然能匹配成功。如图6(a)所示，X(粗实线表示的面目标)为参考数据源的面目标，Y3为(粗虚线表示的线目标)参考数据源的线目标，Y1和Y2(细虚线表示的线目标)为目标数据源的线目标，Z1，Z2为折线Y2上的两个点。使用本文的算法和策略对这几个目标进行匹配的过程是：①遍历参考数据源和目标数据源得到两个目标，不失一般性，假设当前遍历得到的两个目标为X和Y2；②使用面线1∶1匹配算法计算X和Y2的1∶1匹配结果r，X目标上的阴影部分的骨架线应该和Y2目标上的Z1-Z2折线段匹配，因此，对于X与Y2而言，应该是X部分匹配Y2，同时Y2也部分匹配X(r=4)；③r= 4，则X和Y2都有可能跟别的目标匹配，针对X和Y2继续遍历对应的数据集，可以得到X与Y1的面线匹配和Y3与Y2的线线匹配。最终，参考数据源的X，Y3目标与目标数据源的Y1，Y2目标匹配成功，匹配模式为2∶2。弥补了文献[15]和[16]中的面线匹配缺陷，解决面X与线Y2不相交情况下的匹配。

图6 实验数据局部放大

2)对数据误差的适应性强。如图6(b)所示，Q1，Q2(粗实线表示的面目标)为参考数据源的面目标，Q3，Q4(细虚线表示的面目标)为目标数据源的面目标。实际情况是Q1与Q3匹配，Q2与Q4匹配，但是，由于数据误差的影响，Q1与Q4的叠置率却不为零(图6(c)中阴影部分)。本文设置了叠置率阈值Omin，而计算得到的Q1与Q4的叠置率和Q4与Q1的叠置率均小于Omin，故Q1与Q4匹配不成功，不影响Q1与Q3的匹配和Q2与Q4的匹配。

5 结束语

河流和湖泊的匹配是面面、面线和线线相结合的匹配，也是1∶1匹配与非1∶1匹配相结合的匹配。使用本文所研究的面面、面线、线线1∶1匹配算法和非1∶1匹配策略对河流和湖泊数据集进行匹配，取得了良好的匹配效果。在这些算法的基础上，为了提高计算效率，还用到格网索引、MBR等技术，很好的解决了河流和湖泊的匹配问题。

由于目标匹配是为地图更新、变化检测等研究服务的，对地图更新、变化检测等方向的深入研究也是亟需解决的问题，还需要做进一步的努力。

[1] 李德仁, 龚健雅, 张桥平. 论地图数据库合并技术[J]. 测绘科学, 2004, 29(1):1-4.

[2] 翟仁健. 基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D]. 郑州：信息工程大学, 2011.

[3] MASUYAMA A. Methods for Detecting Apparent Differences Between Spatial Tessellationsat Different TimePoints[J]. InternationalJournal of Geographical Information Science, 2006, 20(6):633-648.

[4] YUAN S, TAO C.Development of Conflation Components[A].ProceedingsofGeoinformatics1999 Conference[C]. Ann Arbor, 1999:1-13.

[5] 张桥平, 李德仁, 龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报, 2004, 8(2):107-112.

[6] 郭黎, 崔铁军, 王豪,等. 基于面状要素拓扑关系的数据匹配技术研究[J]. 测绘科学, 2010, 35(1):130-132.

[7] 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2):210-217.

[8] VON G,SESTER G.Change Detection and Integration of Topographic Updates from ATKIS to Geoscientific DataSets[A]. International Conferenceon Next Generation Geospatial Information[C]. Boston, October 2003:19-21.

[9] VAN W,VANPUTTEN F,VANOOSTEROM J,et al.Map Integration-Update Propagation In A Multi-Source Environment[A]. Proceedings of the 5th ACM International Workshop on Advances In Geographic Information Systems[C]. Las Vegas, Nevada, United States,1997:71-76.

[10] WALTER V, FRITSCH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Systems, 1999, 13(5):445-473.

[11] FILIN S, DOYTSHER Y. The Detection of Corresponding Objects In A Linear-Based Map Conflation[J]. Surveying and Land Information Systems,2000,60(2):117-128.

[12] MANTEL D, LIPECK U. Matching Cartographic Objects in Spatial Databases[A]. ISPRS Vol. XXXV, ISPRS Congress, Commission 4[C]. Istanbul, Turkey, July 12-23th, 2004.

[13] 张云菲, 杨必胜, 栾学晨. 利用概率松弛法的城市路网自动匹配[J]. 测绘学报, 2012,41(6):933-939.

[14] TONG Xiaohua, LIANG Dan, JIN Yanmin. A linear road object matching method for conflation based on optimization and logistic regression[J]. International Journal of Geographical Information Science, 2014, 28(4):824-846.

[15] 赵彬彬. 多尺度矢量地图空间目标匹配方法及其应用研究[D]. 长沙：中南大学, 2011.

[16] 赵彬彬, 邓敏, 刘慧敏,等. 多尺度地图的水系面目标与线目标匹配方法与实验[J]. 地球信息科学学报, 2011, 13(3):361-366.

[责任编辑：张德福]

Research on the method of multi-scale vector objects matching for rivers and lakes

ZHONG Dong1, GUO Qingsheng1, WANG Yong2, LIU Jiping2

(1. School of Resource and Environmental Science, Wuhan University, Wuhan 430070, China;2. Chinese Academy of Surveying and Mapping, Beijing 100830，China)

It is important to study the vector object matching method of rivers and lakes in geospatial changing detection and map updating. In this paper, an algorithm on calculating the polyline set in partly matching of line to line is put forward, and based on this and area to area overlay rate, the one to one matching algorithm for area to area, area to line and line to line, and tactics of not one to one matching for rivers and lakes are presented. The matching of the whole dataset of rivers and lakes can be realized. The experiments show that the algorithm and tactics in this paper has two advantages: a.the matching can be resolved when an area does not intersect with a line; b.it has a great adaptation to data error.

multi-cale; rivers; lake; object matching

著录：钟东，郭庆胜，王勇，等.多尺度河流和湖泊的矢量目标匹配方法研究[J].测绘工程，2017，26(10)：70-75.

10.19349/j.cnki.issn1006-7949.2017.10.013

2016-10-14

国家自然科学基金资助项目(41471384);测绘地理信息公益行业科研专项项目(201512032)

钟 东(1992-)，男，硕士研究生.

P208

A

1006-7949(2017)10-0070-06