基于特征参数的DCA-LET结构设计与性能分析

邱丽芳 黄 钢 陈海翔

(北京科技大学机械工程学院， 北京 100083)

基于特征参数的DCA-LET结构设计与性能分析

邱丽芳 黄 钢 陈海翔

(北京科技大学机械工程学院， 北京 100083)

设计了一种基于双C型结构的柔性铰链，称为DCA-LET柔性铰链。定义了影响该柔性铰链性能的特征参数，通过对8组不同特征参数实例的仿真分析，拟合了特征参数与等效弹簧刚度之间的关系，推导了基于该铰链特征参数的等效弹簧刚度的理论计算公式并且引入了修正系数。通过3组实例的理论计算和有限元仿真分析，验证了理论计算公式以及修正系数的正确性。通过对比3组不同特征参数的DCA-LET柔性铰链与内LET柔性铰链的弯曲性能与抗拉性能，得出控制特征参数能够控制该柔性铰链的弯曲性能，同时保证其抗拉压性能并没有明显下降。

DCA-LET； 等效刚度； 特征参数； 柔性铰链； 抗拉性能

引言

柔性(柔顺)机构主要通过柔性构件的变形来进行力或运动的传递[1]。柔顺机构具有加工方便、成本低廉、结构紧凑等特点。平面折展机构(Lamina emergent mechanisms，LEMs)由薄板材料加工制成，可实现在平面外运动的一类柔顺机构[2]。LEMs在电子工业、汽车制造、生物医学、搜救设备等领域有着广泛的应用[3]，在飞机机翼[4]以及太阳能帆板[5]等航空机械方面也具有广阔的应用前景，在微机电系统如细胞夹持装置[6]、升降平台[7]以及机器人关节方面[8]等也有涉及，而柔性机构的设计综合还有待进一步探索与发展。

LEMs主要通过柔性铰链来完成运动与力的传递，故而对柔性铰链的设计非常重要[9]。在LEMs柔性铰链设计方面，国内外学者都作了大量的研究[10-15]。近几年国内对柔性铰链的研究发展较快，如田延岭等[16]对V型柔性铰链进行了研究，陈贵敏等[17]提出了深切口椭圆柔性铰链，于靖军等[18]对柔性铰链设计方法进行了探讨。邱丽芳等[19-21]设计了S型柔性铰链、Triple-LET、S-LET复合型铰链等。

目前，柔性铰链在应用中存在的主要问题是柔度和精度问题，也是柔性铰链设计的关键问题，一般情况下，在提高柔性铰链的弯曲性能时，其抗拉性能往往会下降，并且其转动中心漂移会加大，也就是柔度提高，但精度下降。本文考虑精度，首先设计一种双C型结构的柔性铰链，为了进一步提高双C型结构柔性铰链的弯曲性能，即考虑柔度，设计基于该结构的柔性铰链，称之为DCA-LET柔性铰链，对其弯曲性能进行分析，定义影响该柔性铰链性能的特征参数，推导等效刚度计算公式，在其抗拉压性能下降不明显的情况下，通过控制特征参数来控制铰链的弯曲等效刚度，以期为该铰链的设计提供一种思路。

1 DCA-LET结构设计与等效刚度分析

1.1 结构设计

为提高LET柔性铰链的抗拉压性能，设计双C型结构的柔性铰链(Double C-type flexure hinge，DC-LET)如图1所示。在其抗拉压性能下降不明显的前提下，为了进一步提高双C型结构柔性铰链的弯曲性能，以一定规律去除双C型柔性铰链圆形片段上的部分结构，设计了基于双C型结构的新型柔性铰链(Double C-type flexure hinge with arc gaps， DCA-LET)，其结构如图2所示，设厚度为t，总宽度为W，总长度为L。

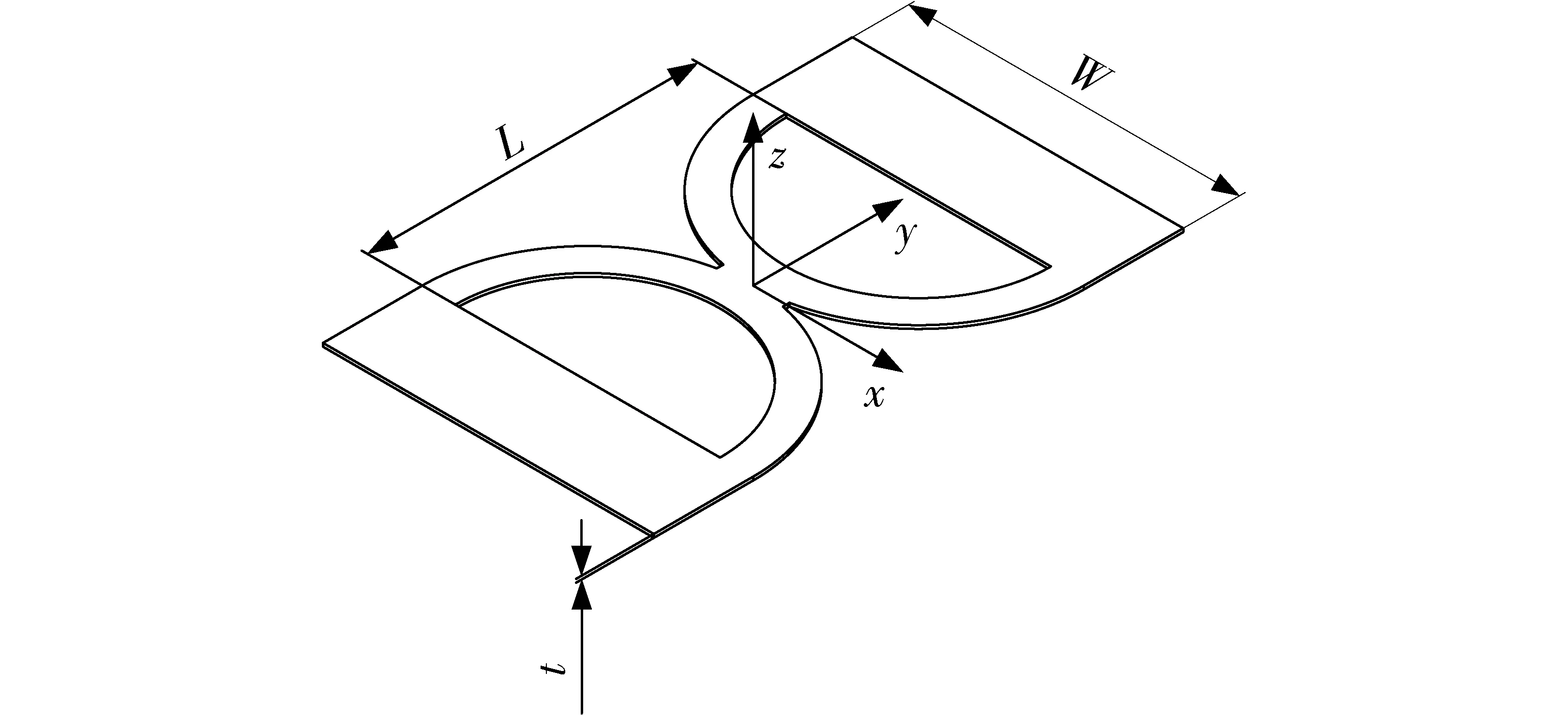
图1 DC-LET柔性铰链三维结构图Fig.1 3D model of DC-LET

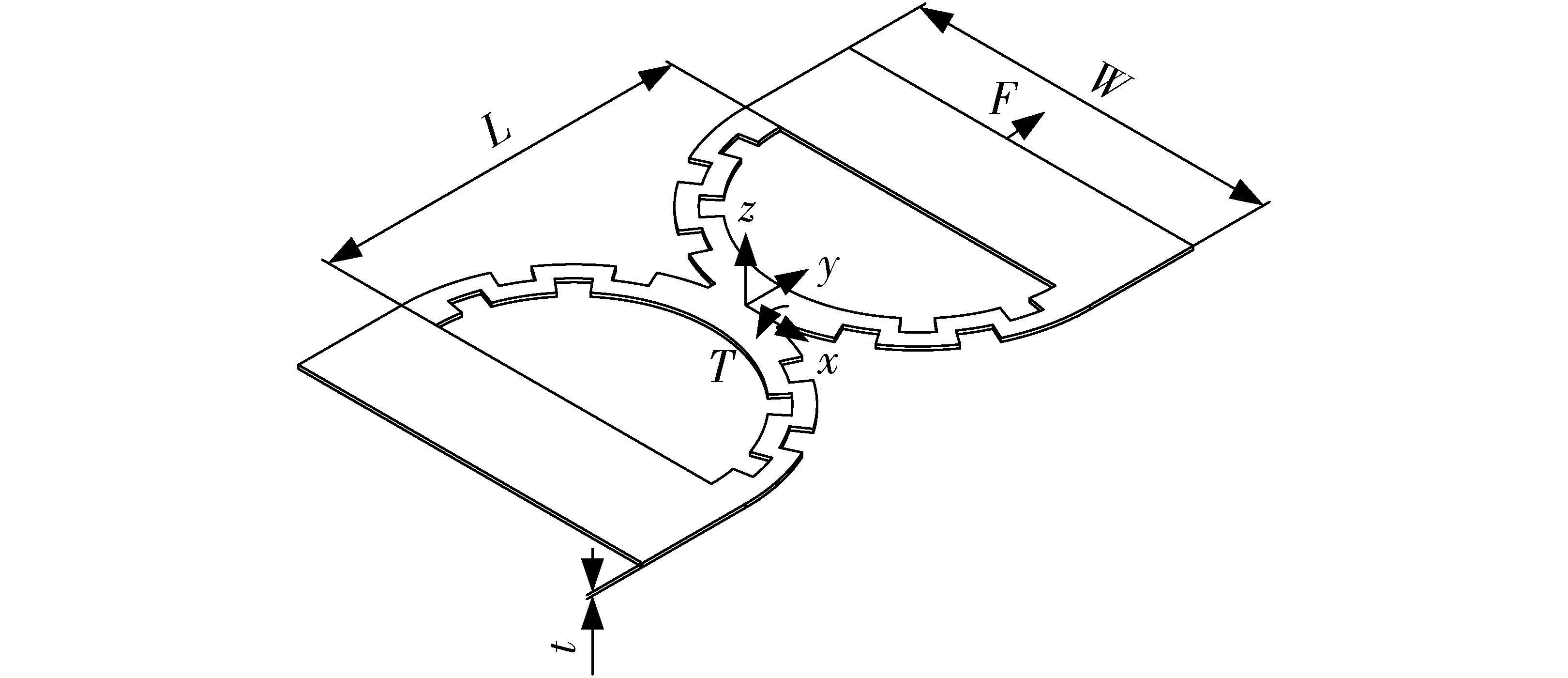
图2 DCA-LET柔性铰链三维结构图Fig.2 3D model of DCA-LET

DCA-LET柔性铰链尺寸示意图如图3所示，根据等效法，柔性片段的等效弹簧模型如图4所示。

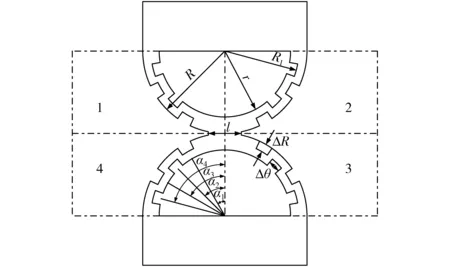
图3 DCA-LET柔性铰链尺寸示意图Fig.3 Dimension labels of DCA-LET

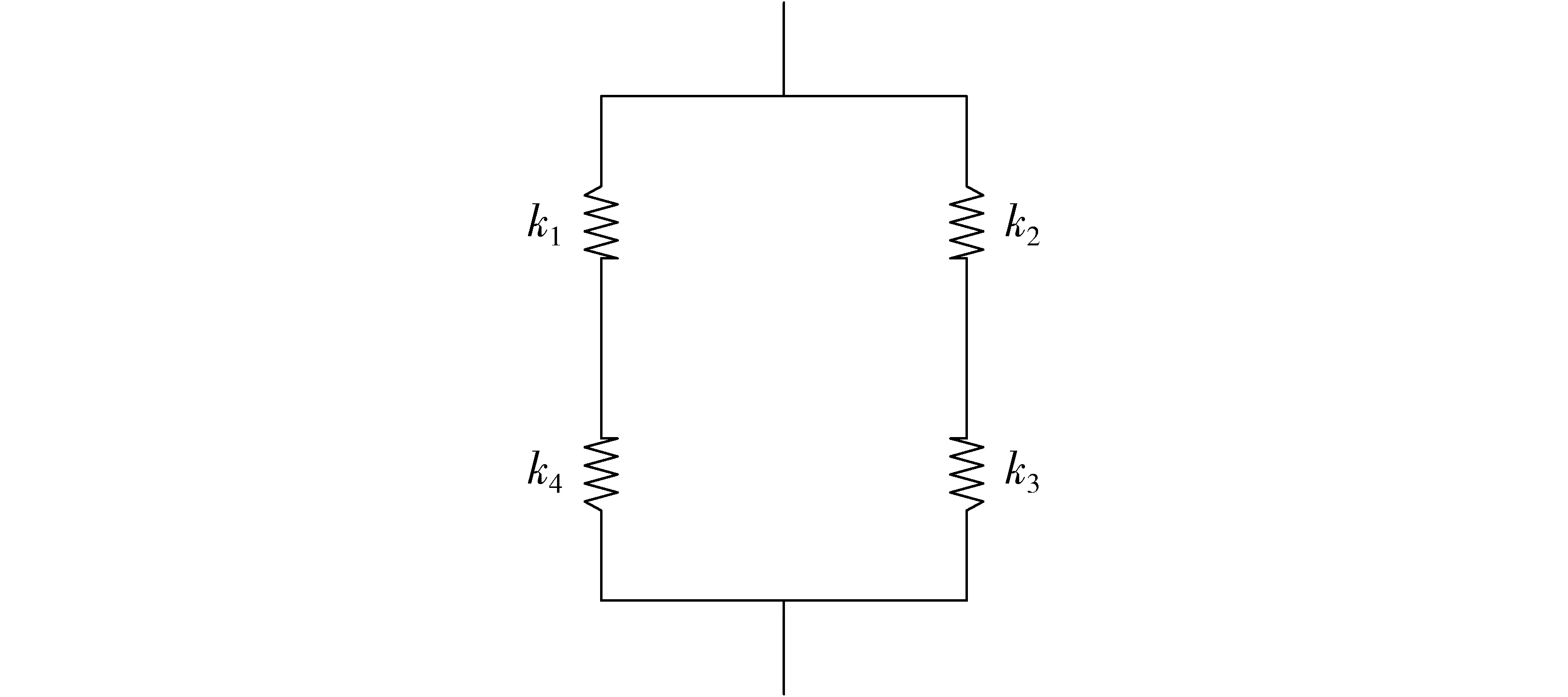
图4 DCA-LET柔性铰链等效弹簧模型Fig.4 Associated spring model of DCA-LET

1.2 等效刚度仿真分析

下面的分析均设定DCA-LET柔性铰链的L为50 mm，W为50 mm，t为0.5 mm。设计DCA-LET柔性铰链尺寸如表1所示。选取材料为铍青铜，其弹性模量E=128 GPa，泊松比ν=0.29，屈服强度[σs]=1 170 MPa。

由于设计的DCA-LET柔性铰链是由DC-LET柔性铰链去除部分结构得到的，因此定义与去除结构相关的尺寸Δθ、ΔR以及去除结构个数为DCA-LET柔性铰链的特征参数，如图3所示。考虑到分析的复杂性，首先确定ΔR为一个定值，并且确定去除结构的具体个数为每四分之一半圆环去除4个结构(图3)，下面讨论特征参数Δθ与等效刚度的关系。

将实例1的特征参数设置为：Δθ=10°，在ABAQUS中建立DCA-LET柔性铰链实例1的有限元仿真模型。图5所示为DCA-LET柔性铰链受到T=178 N·mm的弯矩后所产生的变形量。由图5可得转角θ=1.490 rad(约为86°)，应力为1 149 MPa，小于屈服强度1 170 MPa，铰链变形量在弹性变形量范围之内。

表1 DCA-LET柔性铰链尺寸Tab.1 Dimensions of DCA-LET

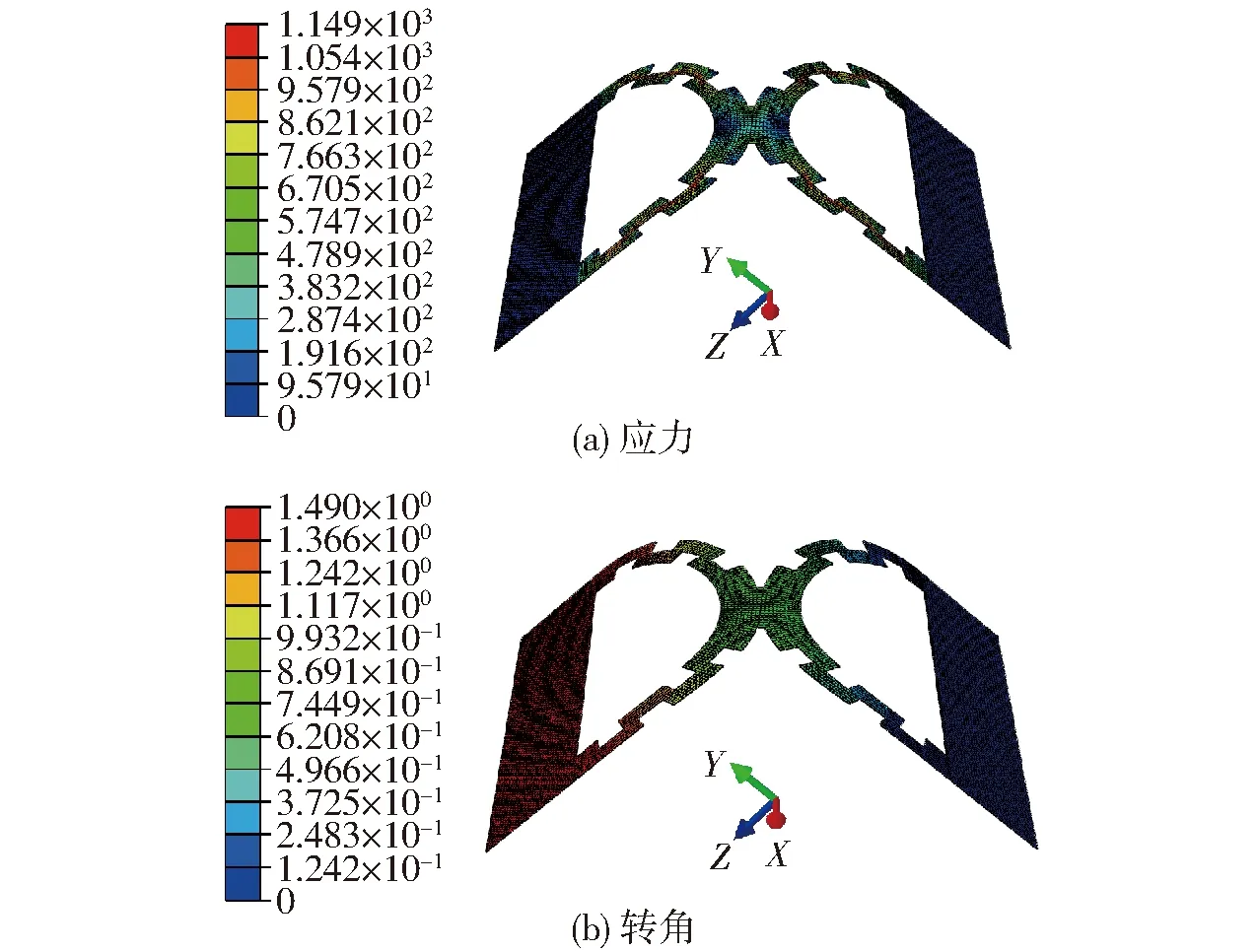
图5 DCA-LET(Δθ=10°)有限元分析Fig.5 Finite element analysis results of DCA-LET(Δθ=10°)

由式(1)可求得特征参数Δθ=10°时DCA-LET

柔性铰链等效刚度仿真值为kf=119.463 N·mm/rad(表2)。

(1)

式中T——作用于铰链的转矩，N·mmθ——柔性铰链转角，rad

设计实例2的特征参数为：Δθ=3°，同样在ABAQUS中建立DCA-LET柔性铰链实例2的有限元仿真模型。同理可得特征参数Δθ=3°时DCA-LET柔性铰链等效刚度仿真值为kf=157.986 N·mm/rad (表2)。

用ABAQUS仿真得到不同特征参数的设计实例3～8的等效刚度仿真值如表2所示，根据表2得到特征参数与等效刚度的关系曲线如图6所示。

表2 不同特征参数DCA-LET柔性铰链等效刚度仿真值Tab.2 Simulation equivalent stiffness of DCA-LET with different characteristic parameters

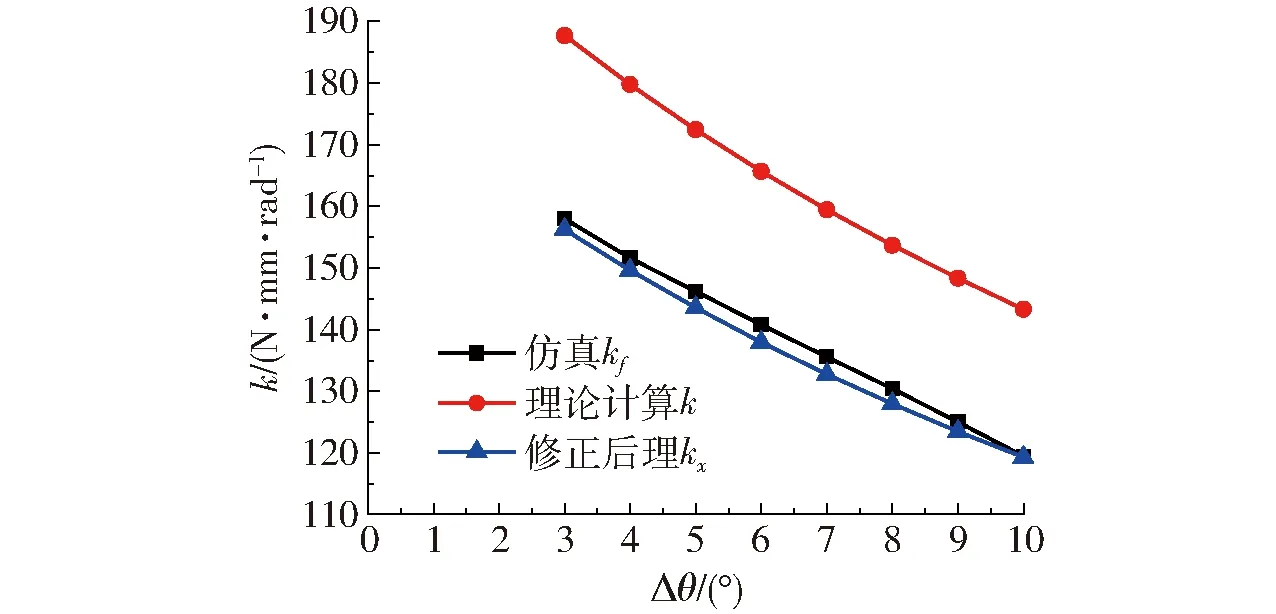
图6 DCA-LET等效刚度与特征参数关系曲线Fig.6 Relationship curves between characteristic parameters and equivalent stiffness of DCA-LET

1.3 等效刚度理论公式推导

依据弹簧的串并联关系，该铰链等效刚度为

(2)

由图3可知，该柔性铰链结构关于x、y轴对称，片段1、2、3、4形状完全相同，若各片段等效刚度用k表示，则式(2)可简化为

keq=k

(3)

图7 DCA-LET柔性片段划分Fig.7 Dividing of DCA-LET segments

当铰链受到如图2所示转矩T时，设图7所示9个片段所产生的变形量分别为θi(i=1,2,…,9)，则总变形量θ为

θ=θ1+θ2+θ3+θ4+θ5+θ6+θ7+θ8+θ9

(4)

根据文献[22]可得

(5)

(6)

(7)

(8)

(9)

将式(4)～(9)代入式(1)中可得DCA-LET柔性铰链的等效刚度理论计算公式为

(10)

简化后可得

(11)

将DCA-LET柔性铰链实例1～ 8不同特征值参数代入式(11)计算得到等效刚度理论值，如图6所示，由图6得到仿真值与理论值曲线趋势基本一致，但不吻合，可能是去除部分结构之后，变形片段的弯扭耦合更加明显所致，为了使理论值更加接近仿真值，引入修正系数μ，修正后的等效刚度为

kx=μk

(12)

设修正系数为μ=0.84，将实例1～8不同特征值的DCA-LET柔性铰链使用式(12)计算得到修正后的等效刚度理论值如图6所示。由图6可知，经过引入修正系数μ进行修正后，等效刚度仿真值与理论值基本吻合。

综上得到修正后等效刚度理论计算公式为

(13)

2 DCA-LET柔性铰链等效刚度理论公式的验证

为验证式(13)的正确性，另取一组外径R和内径r，并取3个不同特征参数的验算实例，如表3所示，其余尺寸同前。设修正系数μ为 0.9，由式(13)计算得到DCA-LET柔性铰链等效刚度理论值，如表3所示。在ABAQUS中建立3个验算实例的有限元仿真模型，得到等效刚度仿真值，如表3所示。

表3 特征参数为Δθ 为6°、8°和10°的DCA-LET柔性铰链等效刚度的仿真值、理论值及相对误差Tab.3 Simulated and theoretical equivalent stiffnesses and their relative error of DCA-LET with characteristic parameter Δθ of 6°, 8° and 10°

设等效刚度理论计算值与仿真值的相对误差为δ，则

(14)

由式(14)计算3个不同特征参数实例的相对误差如表3所示。

由表3可得，铰链等效刚度的有限元仿真值和理论值基本一致，相对误差均在1.4%以内，验证了DCA-LET柔性铰链的等效刚度理论计算公式的正确性。

3 弯曲性能与抗拉性能分析

图8 特征参数Δθ为10°、5.5°和3°的DCA-LET柔性铰链与内LET柔性铰链结构图Fig.8 Schematics of DCA-LET with characteristic parameter Δθ of 10°, 5.5° and 3° and inside LET

为了分析DCA-LET柔性铰链的性能，选取了3个不同特征参数的DCA-LET柔性铰链进行弯曲性能与抗拉性能仿真分析，并且同内LET柔性铰链性能进行对比，3个DCA-LET柔性铰链外形尺寸及内LET柔性铰链外形尺寸同前，如图8所示。通过ABAQUS有限元仿真得到3个特征参数下DCA-LET柔性铰链以及内LET柔性铰链在不同转矩与拉力作用下的转角与位移，如图9、10所示。

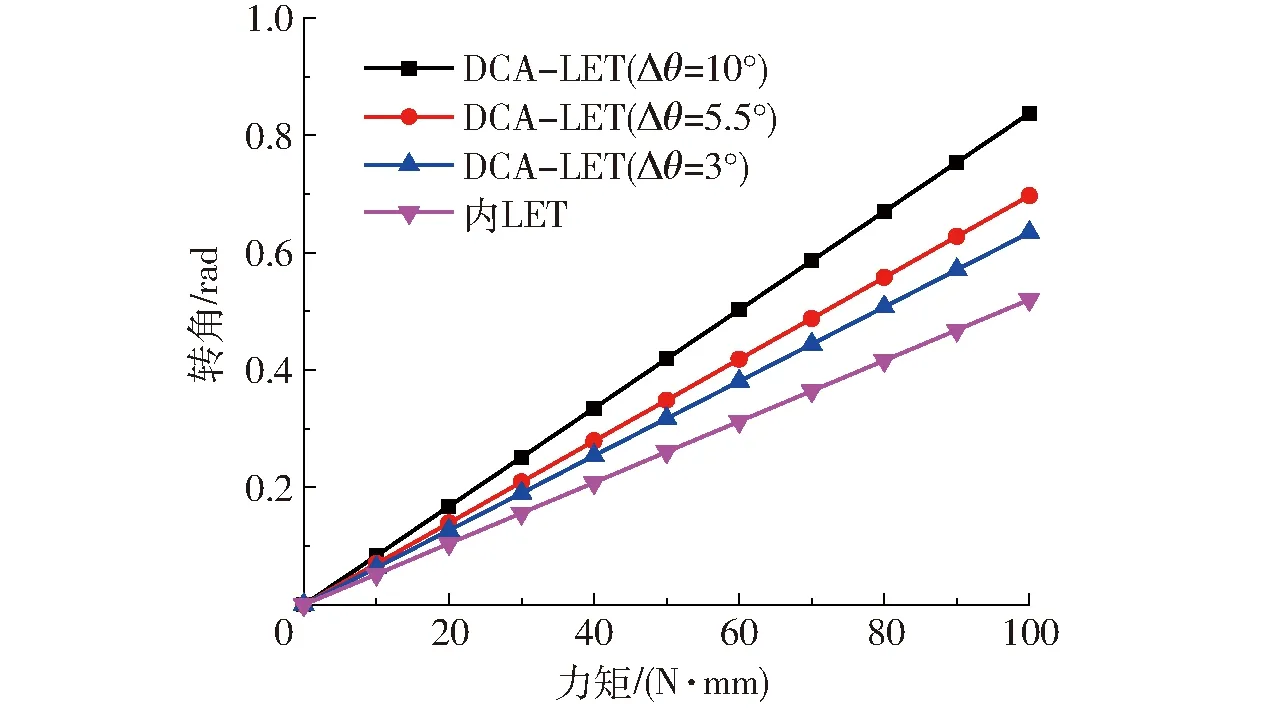
图9 转矩与转角关系曲线Fig.9 Relationship curves between torque and bending angles

图10 拉力与位移关系曲线Fig.10 Relationship curves between force and displacement

由图9、图10可知，DCA-LET柔性铰链在弯曲性能方面均优于内LET柔性铰链，在相同拉力作用下，特征参数Δθ为5.5°与3°的DCA-LET柔性铰链在抗拉性能方面均优于内LET柔性铰链，而特征参数Δθ为10°的DCA-LET柔性铰链的抗拉性能略低于内LET柔性铰链，但其弯曲性能远优于内LET柔性铰链，也优于特征参数Δθ为5.5°与3°的DCA-LET柔性铰链，因此特征参数Δθ为10°的DCA-LET柔性铰链综合性能较好。

4 结论

(1)设计了一种基于双C型结构的柔性铰链，即DCA-LET柔性铰链的结构，定义了影响该铰链特性的特征参数。通过8组实例的仿真分析，得到该铰链等效刚度与一个特征参数的关系曲线，在此基础上推导出了DCA-LET柔性铰链等效刚度的理论计算公式，并引入了修正系数。用3组不同特征参数和外形尺寸实例的理论计算和仿真分析验证了理论计算公式的正确性。

(2)对3个不同特征参数的DCA-LET柔性铰链进行了弯曲性能与抗拉性能仿真分析并与内LET柔性铰链进行了性能对比，得到特征参数Δθ为10°、5.5° 及3°的DCA-LET柔性铰链的弯曲性能均优于内LET柔性铰链，特征参数Δθ为5.5° 与3°的DCA-LET柔性铰链的抗拉性能同样优于内LET柔性铰链，而特征参数Δθ为10°的DCA-LET柔性铰链在抗拉性能方面略低于内LET柔性铰链，但其弯曲性能远优于内LET柔性铰链，因此DCA-LET柔性铰链的综合性能优于内LET柔性铰链。

1 HOWELL L L. Compliant mechanisms[M]. New York: Wiley, 2001.

2 ALBRECHTSEN N B, MAGLEBY S P, HOWELL L L. Identifying potential applications for lamina emergent mechanisms using technology push product development[C]∥ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2010: 513-521.

3 JACOBSEN J O. Fundamental components for lamina emergent mechanisms[D]. Utah:Brigham Young University,2008.

4 LANDON S D, MAGLEBY S P, HOWELL L L. Preliminary concepts for deployable wings on small UAVs using compliance[C]∥ASME 2005 International Mechanical Engineering Congress and Exposition, 2005:353-363.

5 ZIRBEL S A, TREASE B P, MAGLEBY S P, et al. Deployment methods for an origami-inspired rigid-foldable array[C]∥Proceedings of the 40th Aerospace Mechanisms Symposium, NASA Goddard Space Flight Center, 2014:189-194.

6 ATEN Q T, JENSEN B D, BURNETT S H, et al. A self-reconfiguring metamorphic nanoinjector for injection into mouse zygotes[J]. Review of Scientific Instruments, 2014, 85(5):055005-055005-10.

7 邱丽芳，陈家兴，张九俏，等. 平面折展升降柔顺机构设计[J/OL]. 农业机械学报, 2015,46(10): 370-375. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151050&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.10.050. QIU Lifang, CHEN Jiaxing, ZHANG Jiuqiao, et al. Design of lamina emergent elevator mechanism[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(10): 370-375. (in Chinese)

8 田浩, 余跃庆, 吕强. 片簧型柔顺并联机器人运动规划与轨迹跟踪技术[J/OL]. 农业机械学报, 2015, 46(3):372-378.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150354&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.03.054. TIAN Hao, YU Yueqing, LÜ Qiang. Motion planning and trajectory tracking of parallel robot with leaf compliant joint[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3):372-378. (in Chinese)

9 WILDING S E, HOWELL L L, MAGLEBY S P. Spherical lamina emergent mechanisms[J]. Mechanism and Machine Theory, 2012, 49: 187-197.

10 JACOBSEN J O, WINDER B G, HOWELL L L, et al. Lamina emergent mechanisms and their basic elements[J]. Journal of Mechanisms and Robotics, 2010, 2(1): 298-320.

11 TREASE B P, MOON Y M, KOTA S. Design of large-displacement compliant joints [J]. Journal of Mechanical Design, 2005, 127(4): 788-798.

12 FERRELL D B, ISAAC Y F, MAGLEBY S P, et al. Development of criteria for lamina emergent mechanism flexures with specific application to metals[J]. Journal of Mechanical Design, 2011, 133(3): 586-599.

13 JACOBSEN J O, CHEN G, HOWELL L L, et al. Lamina emergent torsional (LET) joint[J]. Mechanism and Machine Theory, 2009, 44(11): 2098-2109.

14 WILDING S E, HOWELL L L, MAGLEBY S P. Introduction of planar compliant joints designed for combined bending and axial loading conditions in lamina emergent mechanisms[J]. Mechanism and Machine Theory, 2012, 56: 1-15.

15 ATEN Q T, JENSEN B D, HOWELL L L. Geometrically non-linear analysis of thin-film compliant MEMS via shell and solid elements[J]. Finite Elements in Analysis and Design, 2012, 49(1): 70-77.

16 TIAN Y, SHIRINZADEH B, ZHANG D. Closed-form compliance equations of filleted V-shaped flexure hinges for compliant mechanism design[J]. Precision Engineering, 2010, 34(3):408-418.

17 陈贵敏, 韩琪. 深切口椭圆柔性铰链[J]. 光学精密工程, 2009, 17(3):570-575. CHEN Guimin, HAN Qi. Deep-notch elliptical flexure hinges[J]. Optics and Precision Engineering, 2009, 17(3):570-575. (in Chinese)

18 于靖军, 裴旭, 毕树生,等. 柔性铰链机构设计方法的研究进展[J]. 机械工程学报, 2010, 46(13):2-13. YU Jingjun, PEI Xu, BI Shusheng, et al. State-of-arts of design method for flexure mechanisms[J]. Journal of Mechanical Engineering, 2010, 46(13):2-13. (in Chinese)

19 邱丽芳, 孟天祥, 张九俏,等. 平面折展机构S形柔性铰链设计与试验[J/OL]. 农业机械学报, 2014, 45(9):324-328.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140952&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2014.09.052. QIU Lifang, MENG Tianxiang, ZHANG Jiuqiao, et al. Design and test of lamina emergent mechanisms S-shaped flexure hinge[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 324-328.(in Chinese)

20 邱丽芳, 印思琪, 谢仲添,等. 基于串联式Triple-LET的LEMs滑块机构分析[J/OL]. 农业机械学报, 2016, 47(6):381-386.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160650&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2016.06.050. QIU Lifang, YIN Siqi, XIE Zhongtian, et al. Analysis of lamina emergent slider mechanism based on the series Triple-LET[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6):381-386.(in Chinese)

21 邱丽芳, 庞大千, 陈家兴,等. S-LET复合型柔性铰链设计与性能研究[J/OL]. 农业机械学报, 2016，47(2):408-412.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160255&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2016.02.055. QIU Lifang, PANG Daqian, CHEN Jiaxing, et al. Design and performance analysis of lamina emergent mechanisms S-LET-shaped flexure hinge[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(2):408-412.(in Chinese)

22 邱丽芳, 韦志鸿, 徐金梧. 新型平面折展机构柔性铰链等效刚度分析[J]. 机械工程学报, 2014，50(17):25-30. QIU Lifang, WEI Zhihong, XU Jinwu. Analysis of equivalent stiffness of new LEMs flexure hinge[J]. Journal of Mechanical Engineering, 2014,50(17):25-30.(in Chinese)

Structure Design and Performance Analysis of DCA-LET Based on Characteristic Parameters

QIU Lifang HUANG Gang CHEN Haixiang

(SchoolofMechanicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China)

LEMs achieve the movement and force transmission through flexure hinges, so it is very important to design flexure hinges. A new type of flexure hinge based on double C-type structure was proposed, named as DCA-LET flexure hinge. The characteristic parameters influencing the performance of the flexure hinge were defined. Based on the simulation analysis of eight examples of different characteristic parameters, the fitting curve of the relationship between the characteristic parameters and the simulation values of the equivalent stiffness was obtained. The theoretical formula of equivalent spring stiffness based on the characteristic parameters of the hinge was deduced and the correction factor was introduced. The correctness of theoretical calculation formula and correction factor was verified by theoretical calculation and finite element simulation of three examples. The bending and tensile properties of three DCA-LET flexure hinges with different characteristic parameters and inside LET flexure hinge were compared, and the results showed that the DCA-LET flexure hinge had better overall performance than the LET flexure hinge. The characteristic parameters can control the bending performance of DCA-LET hinge, and its tensile and compression properties had no significant decrease, which provided an effective method for the design of the flexure hinges.

DCA-LET; equivalent stiffness; characteristic parameters; flexure hinge; anti-tensile performance

10.6041/j.issn.1000-1298.2017.08.048

2017-01-14

2017-03-08

国家自然科学基金项目(51475037)

邱丽芳(1966—)，女，教授，主要从事机械设计及理论和柔顺机构研究，E-mail： qlf@ustb.edu.cn

TH122

A

1000-1298(2017)08-0399-06