番茄粘弹性参数机器人抓取在线估计
周 俊 张 娜 孟一猛 王明军
(南京农业大学江苏省智能化农业装备重点实验室, 南京 210031)
番茄粘弹性参数机器人抓取在线估计
周 俊 张 娜 孟一猛 王明军
(南京农业大学江苏省智能化农业装备重点实验室, 南京 210031)
为了使采摘机器人在抓取过程中能够对被抓果蔬的粘弹性力学参数进行快速估计,实时优化抓取过程,减少末端执行器对被抓取对象造成机械损伤,以抓取力、变形量、作用时间为输入,建立了番茄粘弹性参数估计的人工神经网络模型。运用质构仪蠕变试验所测的力、变形和时间,以及粘弹性参数E1、E2、η1、η2作为训练数据集,确定了人工神经网络的拓扑结构和参数,并测试了网络模型的粘弹性参数估计性能。利用二指机器人末端执行器对随机番茄样本进行抓取试验,并在抓取过程中用此模型来在线估计粘弹性参数。通过与质构仪的实测值进行对比发现,当时间t≥0.2 s时,各参数的估计值与实测值之间的相对误差均在25%以内,并根据0.2 s时得到的粘弹性参数对机器人抓取力范围进行了估计。结果表明,利用此方法在机器人抓取过程中可以对被抓番茄粘弹性特性进行估计,为在线优化抓取力提供了依据。
机器人抓取; 番茄; 粘弹性参数; 蠕变试验; 人工神经网络
引言
在果蔬采摘、分级、包装和加工等作业环节中,机器人经常通过末端执行器的手指直接对果蔬施加作用力来实现果蔬的稳定夹持抓取。而果蔬是一种粘弹性体,同时具有弹性和粘性两种不同机理的形变[1],研究果蔬的粘弹性,不仅可以减少果蔬抓取过程中的机械损伤,也为抓取部件的设计提供依据,同时为采摘机器人实现快速抓取提供必要信息[2-4]。
国内外学者对各类果蔬的粘弹特性进行了许多研究。CHEN等[5]和KAUR等[6-7]分别建立了梨和马铃薯的Maxwell粘弹性力学模型,并通过试验求得相应的粘弹性参数。SAEIDIRAD等[8]利用质构仪对不同品种石榴分别做应力松弛试验,利用人工神经网络方法代替麦克斯韦模型来预测石榴的粘弹特性。张谦益等[9]和杨晓清等[10]通过试验分别得到梨果实和河套蜜瓜的蠕变模型及相应的粘弹性参数,并对影响蠕变量的因素进行了分析。李小昱等[11]和刘继展等[12]针对经典Burger’s模型在蠕变特性表达中的不足,分别在Burger’s模型基础上建立了四元件五参数和四元件六参数的修正模型。此外,李小昱等[11]还通过试验发现苹果的粘弹性参数与损伤体积有着显著的线性相关关系。郭文斌等[13]对马铃薯完整块茎进行压缩试验,得到了马铃薯整茎淀粉含量与粘弹性参数之间的回归方程,为利用粘弹性力学参数估测马铃薯淀粉含量提供了参考。杨玲等[14]和方媛等[15]分别对“华红”苹果和“红富士”苹果进行蠕变测试,分析了粘弹性参数与苹果果实质构特性和营养成分的相关性,完善了苹果果实品质评价体系。
虽然国内外学者对多种果蔬的粘弹性力学特性进行了研究,但是现有的研究几乎都是通过传统的试验方法来求取粘弹性参数,而基于采摘机器人利用机器学习方法获取果蔬粘弹性参数的研究却很少。为了使采摘机器人抓取过程中能够在尽可能短的时间内对被抓果蔬的粘弹性力学参数进行估计,可以为在线优化抓取控制提供信息,本文构建估计粘弹性参数的人工神经网络模型,通过机器人两指末端执行器抓取试验验证所建模型的有效性,得到估计果实粘弹性力学特性的最短时间,在此基础上对机器人抓取力范围进行估计。
1 蠕变实验
1.1 实验材料
选用材料为皖粉2号番茄。根据商业行业标准SB/T 10331—2000中关于番茄成熟期的界定,选择红熟前期(果实着红面为10%~30%)、红熟中期(果实着红面为40%~60%)番茄各10个,番茄的赤道直径(垂直于果柄方向)在72~80 mm之间,质量在166~252 g之间。番茄蠕变测试采用美国FTC公司的TMS-PRO型食品物性分析仪(质构仪)。
1.2 实验方法
由于番茄在采摘、运输、加工等作业环节中,一般都是处于完整状态下承受外载荷作用,故对完整番茄果实进行蠕变实验。
蠕变测试参数设置为:探头P75(直径75 mm),起始力0.6 N,加载时间30 s,测试速度60 mm/min,数据采集频率10 Hz。被测番茄果柄呈水平状放置,用底座固定。每个样本大致在果腰处随机选取3个相邻间隔约120°的点分别用3、5、7 N的力进行蠕变实验,共进行60次蠕变实验,图1为蠕变实验装置。

图1 蠕变实验装置Fig.1 Platform of creep experiment
蠕变实验中所得的变形与时间关系曲线可以由不同的蠕变模型来描述,如Maxwell模型、Kelvin模型、Burgers模型等。其中Burgers模型是表征粘弹性材料蠕变特性的经典模型,它是由一个Maxwell单元和一个Kelvin单元通过串联组成的四元件模型,其结构如图2所示。Burgers模型可以表示粘弹性的主要特征,是预测物料蠕变特性的最著名模型之一[16],故本文选用Burgers模型来描述番茄蠕变加载过程中的蠕变特性。
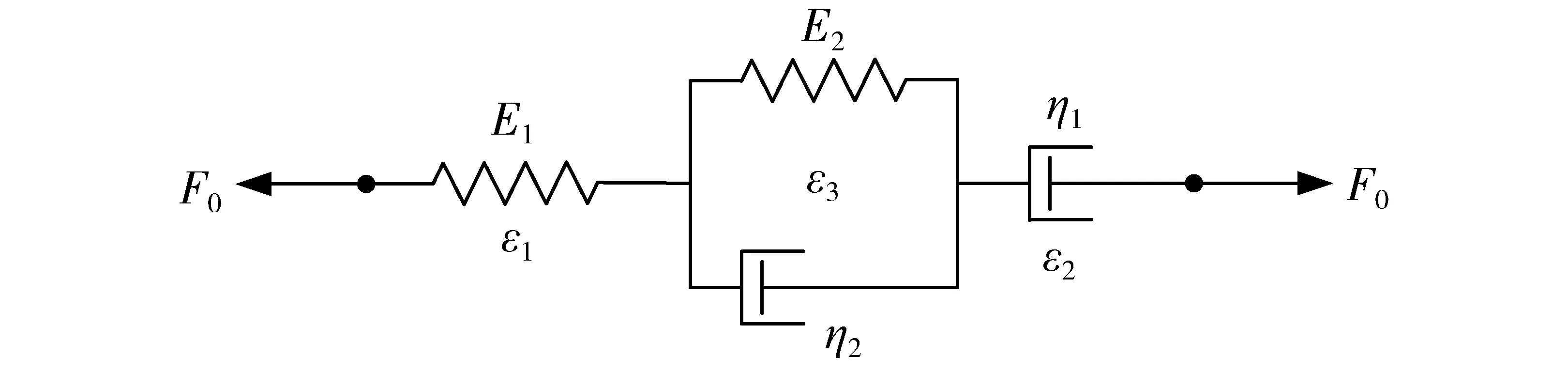
图2 Burgers模型Fig.2 Burgers model
Burgers模型蠕变加载过程的微分方程为
(1)
式中D(t)——变形量,mmt——时间,sF0——恒定载荷,NE1——瞬时弹性系数,N/mmE2——延迟弹性系数,N/mmη1——串联粘性系数,N·s/mmη2——并联粘性系数,N·s/mm
1.3 蠕变模型参数求取
通过蠕变实验可以得到变形-时间的关系曲线,即蠕变曲线,60次蠕变实验可以得到60条蠕变曲线。使用Origin 8.0软件中的非线性拟合工具箱,利用式(1)蠕变模型微分方程对番茄蠕变实验数据进行拟合,即得番茄样本蠕变模型的粘弹性参数和决定系数。拟合结果表明,决定系数R2均高于0.99,验证了所选模型的有效性。图3为从20个番茄样本中随机选取的一个样本分别在3、5、7 N力作用下的蠕变曲线和拟合曲线,得到相应的粘弹性参数和决定系数如表1所示。其余番茄样本的蠕变曲线及拟合曲线情况类似。

图3 蠕变曲线与拟合曲线Fig.3 Creep curve and fitting curve
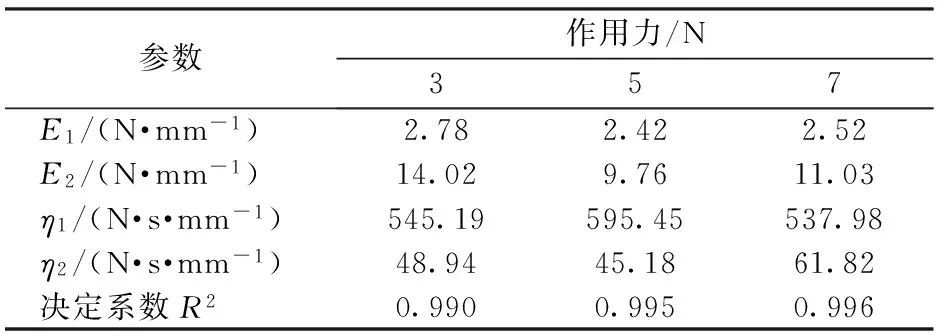
参数作用力/N357E1/(N·mm-1)2.782.422.52E2/(N·mm-1)14.029.7611.03η1/(N·s·mm-1)545.19595.45537.98η2/(N·s·mm-1)48.9445.1861.82决定系数R20.9900.9950.996
2 粘弹性参数估计模型建立
2.1 人工神经网络
人工神经网络是由大量简单的处理单元通过广泛连接组成的复杂网络。这里采用前馈型神经网络,通过反向传播算法(BP算法)来实现。BP神经网络由输入层、隐含层和输出层构成,能实现从输入空间到输出空间的非线性映射,可以逼近任意非线性系统[17]。标准的3层前馈人工神经网络的拓扑结构如图4所示,ωij和ωjk分别是输入层与隐含层、隐含层与输出层之间的连接权值。

图4 3层前馈人工神经网络的拓扑结构Fig.4 Topological structure of three layers feed forward artifical neutral network
2.2 粘弹性参数网络估计模型设计
2.2.1 网络模型拓扑结构
番茄粘弹性参数估计模型选用3层人工神经网络结构。其中,输入层和隐含层之间的传递函数为Tansig,即f(x)=tanh(x);隐含层和输出层之间的传递函数为Purelin,即f(x)=kx。
输入层和输出层的节点数分别由输入变量和输出变量的个数决定。由于模型的输入变量为加载力F、变形量D和加载时间t,输出量为粘弹性参数E1、E2、η1、η2,故输入层和输出层的节点数分别为3和4。根据Kolmogorov定理确定隐含层节点数理论值为7,经过反复训练对比发现最佳隐含层节点数为11,所以确定所建模型网络拓扑结构为3-11-4。
2.2.2 网络模型训练
从每次质构仪蠕变实验数据中取10组数据作为样本数。为了模拟机器人抓取过程,其中在这次蠕变实验过程中随机选择加载时间t数据,与对应加载力F、变形量D构成1组输入量。根据这次蠕变实验数据应用曲线拟合方法得到的粘弹性参数作为这10组数据的共同输出量。这样便拥有了600组样本数据。
对网络的输入样本数据和输出样本数据进行预处理可以消除量纲影响,提高网络收敛性能[18]。因此对数据进行归一化处理,把所有数据都转换为[0,1]区间的数。运用最大最小法对数据进行归一化处理
xk=(xk-xmin)/(xmax-xmin)
(2)
式中xk——数据序列中第k个数xmin——数据序列中的最小数xmax——数据序列中的最大数
选用均方误差MSE作为目标评价网络模型性能
(3)
式中M——均方误差N——训练样本数ei——第i个样本的训练误差Ti——第i个训练样本的目标输出Yi——第i个训练样本的网络输出
设定学习率为0.01,终止训练步数为1 000,从600组样本数据中随机选择500组数据为训练数据,其余100组数据为测试数据,对神经网络模型进行训练。训练数据的相关系数分别为0.93、0.92、0.93和0.93,均方误差为0.033。
2.2.3 网络模型性能分析
用100组测试样本数据对网络模型进行性能评价,网络预测输出的相对误差如图5所示。由于样本中的时间t是随机分布的,故各参数的相对误差都有一定波动,一般与蠕变初始时刻对应的样本形变量小、蠕变过程不充分等原因有关,误差会比较大。由图5可知,瞬时弹性系数E1的相对误差均在15%以内,预测效果较好;延迟弹性系数E2和串联粘性系数η1的相对误差波动较大,但相对误差大于25%的概率都低于10%;并联粘性系数η2的相对误差大于25%的概率为4%。可见,该网络模型可以应用实测的力、变形量与时间3个数据来近似估计果蔬的粘弹性参数,使粘弹性参数的求取具有一定的实时性,从而为在线优化抓取控制过程提供了基础。

图5 网络预测输出的相对误差Fig.5 Relative error of network predicted output
3 机器人抓取在线估计番茄粘弹性参数
3.1 机器人抓取试验
试验平台采用德国SCHUNK公司生产的WSG 50型二指机器人末端执行器,该末端执行器集成了控制器、编码器和SD存储卡,与PC机的通讯协议为TCP/IP协议,手指材质为铝合金。其中一个手指上装有力反馈传感器,抓取过程中可以实时测量抓取力,手指位移由编码器实时测量。试验平台如图6所示。

图6 抓取试验平台Fig.6 Grasping experimental platform1.信息采集系统 2.WSG 50型机械手 3.力反馈手指 4.稳压电源
使用Visual Studio 2010软件开发末端执行器的控制软件,可以实现对抓取速度、加速度、力和位移的调控,能够实时记录手指位移、抓取力及抓取时间等数据。
随机选择红熟前期、红熟中期番茄各2个,机械手以恒定的速度对这4个番茄样本分别进行抓取试验,当抓取力达到设定停止力后,手指停止移动保持自锁直至释放果实,记录抓取过程中力、位移与时间的数据。试验设定的停止力Ft为最小抓取力。
Ft=mgα/(2μ)
(4)
式中Ft——停止力m——番茄质量g——重力加速度α——安全因子,取α=1.5μ——番茄与机器手之间的摩擦因数,试验测得μ为0.22
3.2 番茄粘弹性参数在线估计结果与分析
将抓取过程前0.6 s的试验数据分别输入粘弹性参数估计模型,在线计算番茄样本的粘弹性参数。估计计算结果与通过质构仪数据拟合测得的粘弹性参数对比情况如表2所示。
番茄粘弹性参数网络模型在线估计值与质构仪数据离线测量值之间的相对误差如图7所示。可见,弹性系数E1的相对误差均在22%以内;当t=0.1 s时,E2、η1和η2的相对误差波动较大,但当t≥0.2 s时,E2、η1和η2的相对误差虽有波动但都在25%以内,趋于稳定。误差的来源既有粘弹性参数估计神经网络模型的计算误差,也有传感器等在线测量的误差。虽然,这样得到的粘弹性参数估计值误差还不太理想,但相对完全未知的抓取而言,这个估计值对判断被抓取对象物理特性提供了一定的信息,可以为采摘机器人在线优化抓取过程提供依据。
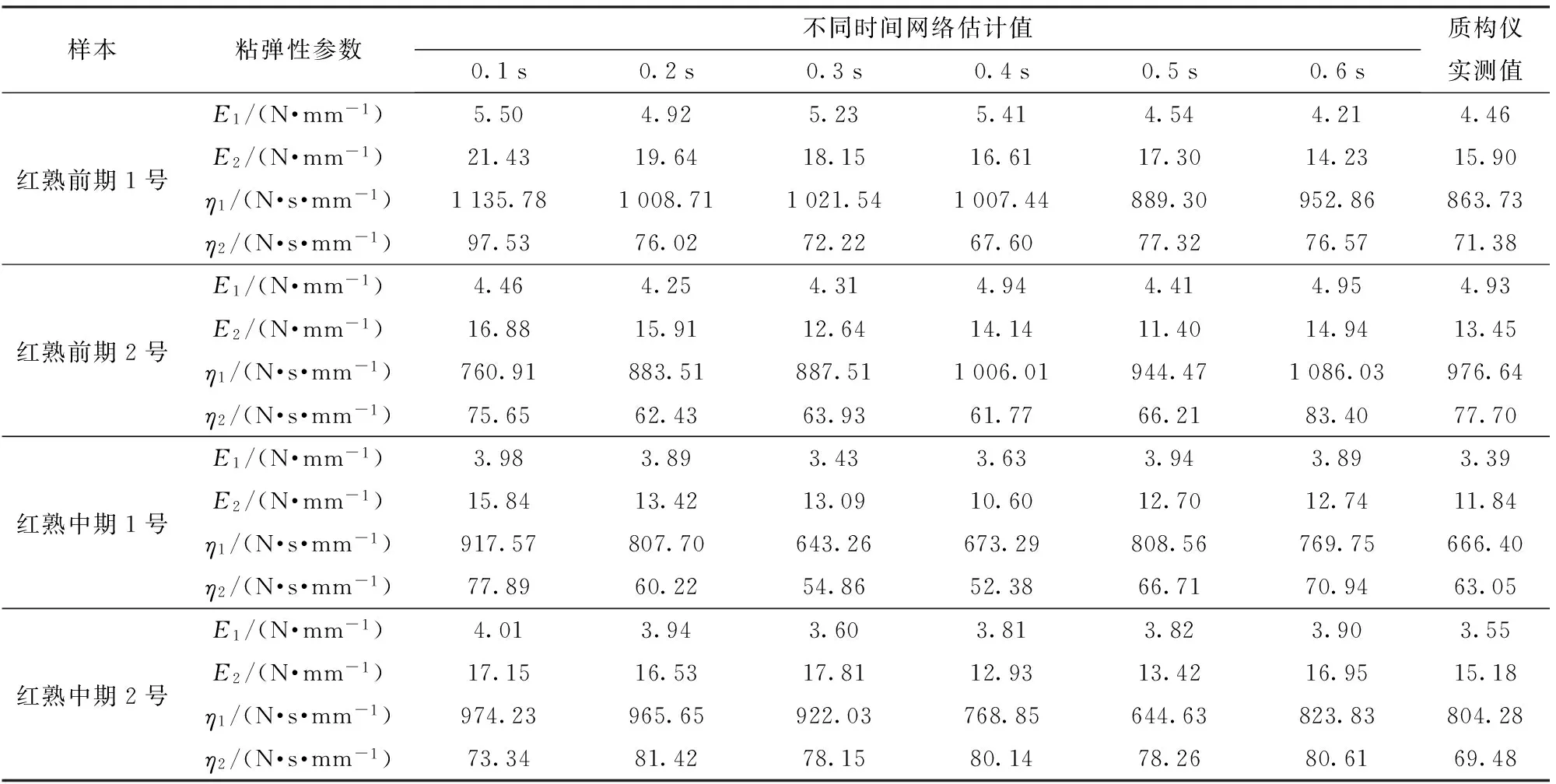
表2 估计值和实测值Tab.2 Estimated values and measured values
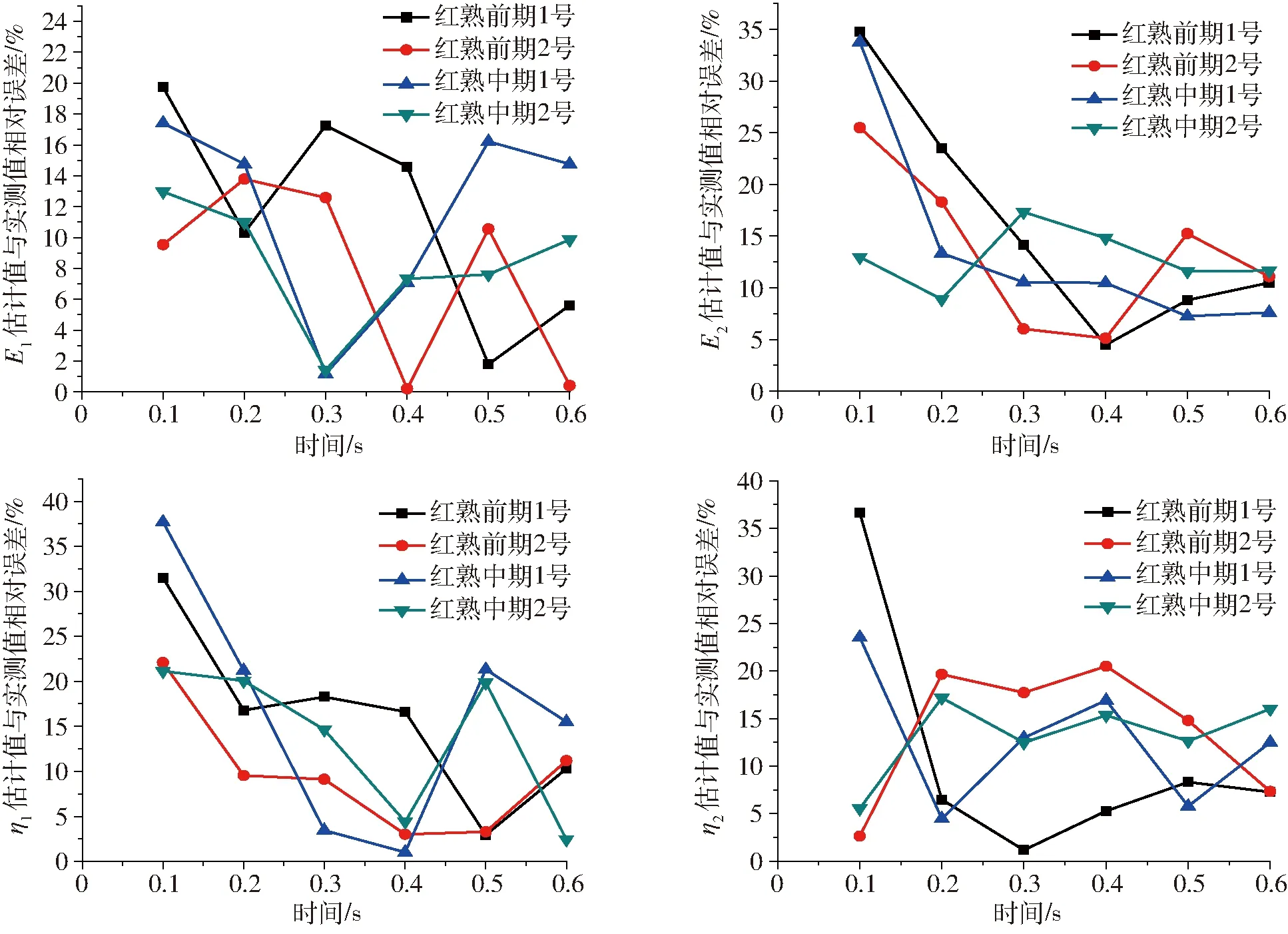
图7 相对误差曲线Fig.7 Relative error curves of estimated values
由于在线优化需要能够尽快对被抓对象粘弹性力学特性进行估计,因此,可将0.2 s时的抓取力、变形量和时间输入已训练好的人工神经网络模型来估计粘弹性参数,为在线优化抓取控制策略提供参数依据。
3.3 基于番茄粘弹性参数的机器人抓取力范围估计
由式(1)可知,抓取停止时的番茄变形量为
(5)
抓取过程结束时番茄的压缩率为
(6)
式中L——接触处番茄样本的直径
由式(5)、(6)可得抓取力为
(7)
李智国等[19-20]通过试验发现影响番茄机械损伤度最大的因素是压缩率,压缩率每增加1%,番茄的机械损伤度平均增加2.98%;当压缩率水平分别为4%和8%时,番茄以弹性变形为主,当压缩率水平分别为12%和16%时,番茄以塑性变形为主。为减少采摘过程中番茄的机械损伤,以番茄的压缩率不高于4%为条件,即C≤4%。这样,根据0.2 s时得到的粘弹性参数就可以对机器人抓取力范围进行估计。
综合考虑抓取稳定性和番茄的压缩率水平,由式(4)、(7)可得机器人抓取力范围为
(8)
通常情况下人工完成单次稳定抓取动作的时间为1 s,日本采摘机器人完成稳定抓取的时间大约为4 s[21]。因此,以机器人完成抓取过程时间持续2 s为例,可以计算出抓取力范围如表3所示。

表3 抓取力范围Tab.3 Range of grasp force
在实际抓取过程中,可利用0.2 s时估计得到的粘弹性参数来计算抓取力上限,结合稳定抓取的最小抓取力来在线选取抓取范围,以实现在稳定抓取前提下避免造成番茄机械损伤。
4 结论
(1)以力、变形和时间为输入,粘弹性参数E1、E2、η1、η2为输出,构建了估计番茄粘弹性参数的人工神经网络模型。确定网络的拓扑结构为3-11-4,并利用质构仪的蠕变试验数据对网络进行训练。
(2)利用二指机器人末端执行器对随机选择的番茄样本进行抓取试验,记录试验过程中力、变形量随时间变化的数据,将不同时刻的试验数据分别输入粘弹性参数估计模型,计算输出番茄的粘弹性参数。与质构仪实测值相比,抓取0.2 s以后,粘弹性参数估计值相对误差小于25%。
(3)在番茄压缩率不高于4%条件下,利用0.2 s估计得到的粘弹性参数计算出机器人抓取力的取值范围,为避免抓取过程中造成番茄机械损伤提供了理论依据。
1 TSAI C H D, KAO I, SHIBATA A, et al. Experimental study of creep response of viscoelastic contact interface under force control[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems,2010, 6219(1):4275-4280.
2 邓云, 吴颖, 李云飞. 果蔬在贮运过程中的生物力学特性及质地检测[J]. 农业工程学报, 2005, 21(4):1-6. DENG Yun, WU Ying, LI Yunfei. Biomechanical properties and texture detection of fruits and vegetables during storage and transportation[J]. Transactions of the CSAE, 2005, 21(4):1-6. (in Chinese)
3 李成, 马小愚, 雷溥. 番茄果实力学特性及与成熟度关系的试验研究[J]. 农机化研究, 2006(1):167-169. LI Cheng, MA Xiaoyu, LEI Pu. Study on the relationship between mechanical and theological properties and ripe degree of tomato[J]. Journal of Agricultural Mechanization Research, 2006(1):167-169. (in Chinese)
4 刘继展, 李萍萍, 李智国,等. 面向机器人采摘的番茄力学特性试验[J]. 农业工程学报, 2008, 24(12):66-70. LIU Jizhan, LI Pingping, LI Zhiguo, et al. Experimental study on mechanical properties of tomatoes for robotic harvesting [J]. Transactions of the CSAE, 2008, 24(12):66-70. (in Chinese)
5 CHEN P, FRIDLEY R B. Analytical method for determining viscoelastic constants of agricultural materials[J]. Transactions of the ASAE, 1972, 15(6):1103-1106.
6 KAUR L, SINGH N, NAVDEEP S S, et al. Some properties of potatoes and their starches I. cooking, textural and rheological properties of potatoes[J]. Food Chemistry, 2002, 79(2):177-181.
7 SINGH J, KAUR L, RAO M A. Textural and rheological characteristics of raw and cooked potatoes[M]∥SINGH J, KAUR L, RAO M A.Advances in potato chemistry and technology. Amsterdam: Elsevier Inc,2009:249-271.
8 SAEIDIRAD M H, ROHANI A, ZARIFNESHAT S. Predictions of viscoelastic behavior of pomegranate using artificial neural network and Maxwell model[J]. Computers & Electronics in Agriculture, 2013, 98:1-7.
9 张谦益, 吴洪华. 梨果实蠕变基本流变特性研究[J]. 现代食品科技, 2006, 22(4):46-48. ZHANG Qianyi, WU Honghua. The creep rheological properties of pear[J]. Modern Food Science and Technology, 2006, 22(4):46-48. (in Chinese)
10 杨晓清, 王春光. 河套蜜瓜静载蠕变特性的试验研究[J]. 农业工程学报, 2007, 23(3):202-207. YANG Xiaoqing, WANG Chunguang. Creep properties of Hetao muskmelon under static loading[J]. Transactions of the CSAE, 2007, 23(3):202-207. (in Chinese)
11 李小昱, 朱俊平, 王为,等. 苹果蠕变特性与静载损伤机理的研究[J]. 西北农林科技大学学报:自然科学版, 1997,25(6):64-68. LI Xiaoyu, ZHU Junping, WANG Wei, et al. A study on creep properties and static loading damage mechanisms of apple[J]. Journal of Northwest A&F University: Natural Science Edition, 1997,25(6):64-68. (in Chinese)
12 刘继展, 白欣欣, 李萍萍. 番茄果实蠕变特性表征的Burger’s修正模型[J]. 农业工程学报, 2013,29(9):249-255. LIU Jizhan, BAI Xinxin, LI Pingping. Modified Burger’s model for describing creep behavior of tomato fruits[J]. Transactions of the CSAE, 2013,29(9):249-255. (in Chinese)
13 郭文斌, 王春光, 高晶晶. 马铃薯整茎压缩模型的建立与参数分析[J]. 农机化研究, 2014, 36(1): 190-193. GUO Wenbin, WANG Chunguang, GAO Jingjing. Study on correlation between starch content and parameters in viscoelastic model of potato tuber[J]. Journal of Agricultural Mechanization Research, 2014, 36(1): 190-193. (in Chinese)
14 杨玲, 张彩霞, 康国栋,等. ‘华红’苹果果肉的流变特性及其主成分分析[J]. 中国农业科学, 2015, 48(12):2417-2427. YANG Ling, ZHANG Caixia, KANG Guodong, et al. Rheologic properties of ‘Huahong’ apple pulp and their principal component analysis[J]. Scientia Agricultura Sinica, 2015, 48(12):2417-2427. (in Chinese)
15 方媛, 赵武奇, 张清安,等. ‘红富士’苹果蠕变特性与果实品质的相关分析[J]. 中国农业科学, 2016, 49(4):717-726. FANG Yuan, ZHAO Wuqi, ZHANG Qingan, et al. The correlation analysis between quality and creep property of ‘Fuji’ apple[J]. Scientia Agricultura Sinica, 2016, 49(4):717-726. (in Chinese)
16 杨明韶. 农业物料流变学[M]. 北京:中国农业出版社, 2010.
17 徐丽娜. 神经网络控制[M]. 北京:电子工业出版社, 2009.
18 陈小前, 罗世彬, 王振国,等. BP神经网络应用中的前后处理过程研究[J]. 系统工程理论与实践, 2002, 22(1):65-70. CHEN Xiaoqian, LUO Shibin, WANG Zhenguo, et al. Research on preprocessing and postprocessing of the application of BP neural network[J]. System Engineering Theory and Practice, 2002, 22(1):65-70.(in Chinese)
19 李智国, 刘继展, 李萍萍. 机器人采摘中番茄力学特性与机械损伤的关系[J]. 农业工程学报, 2010, 26(5):112-116. LI Zhiguo, LIU Jizhan, LI Pingping. Relationship between mechanical property and damage of tomato during robot harvesting[J]. Transactions of the CSAE, 2010,26(5): 112-116. (in Chinese)
20 李智国. 基于番茄生物力学特性的采摘机器人抓取损伤研究[D]. 镇江:江苏大学, 2011. LI Zhiguo. Study on the grasp damage of harvesting robot based on the biomechanical properties of tomato fruits[D]. Zhenjiang: Jiangsu University, 2011. (in Chinese)
21 李智国. 番茄采摘机器人夹持系统的加减速过程研究[D]. 镇江:江苏大学, 2009. LI Zhiguo. Acceleration and deceleration process of the grip system on tomato harvesting robot[D].Zhenjiang: Jiangsu University,2009. (in Chinese)
Online Estimation of Tomato Viscoelastic Parameters during Robot Grasping
ZHOU Jun ZHANG Na MENG Yimeng WANG Mingjun
(KeyLaboratoryofIntelligentAgriculturalEquipmentinJiangsuProvince,NanjingAgriculturalUniversity,Nanjing210031,China)
When a picking robot is able to quickly estimate the viscoelastic parameters of the fruits and vegetables in the process of grasping, an optimization of the grasping process in real time can be carried out and the mechanical damage caused by the end-effector can be alleviated. Artificial neural network (ANN) model of tomato viscoelastic parameters estimation was established by using grasping force, deformation and acting time as inputs. The force, deformation and time measured by creep test with texture analyzer, as well as the viscoelastic parameters (E1,E2,η1,η2) were used as the training data set to determine the topological structure and parameters of the artificial neural network. Then performance of the network model was tested. A two finger robot end-effector was applied to grasp tomato samples selected randomly, and the ANN model was used to estimate the viscoelastic parameters online during the process of grasping. Compared with the measured value by texture analyzer, when time was more than or equal to 0.2 s, the relative error between the estimated value and the measured value were less than 25%, and according to the viscoelastic parameters obtained from the 0.2 s time, the range of the robot’s grasping force was estimated. The results showed that the method could be used to estimate the viscoelastic properties of the grasped tomatoes during the robot grasping process, which provided the basis for the online optimization of grasping force.
robot grasping; tomato; viscoelastic parameters; creep experiment; artificial neural network
10.6041/j.issn.1000-1298.2017.08.002
2016-12-21
2017-03-20
国家自然科学基金项目(31471419)、高等学校博士学科点专项科研基金博导类项目(20130097110043)和浙江省自然科学基金项目(LY17F030006)
周俊(1974—),男,教授,博士生导师,主要从事农业机器人和机器视觉与模式识别研究,E-mail: zhoujun@njau.edu.cn
TP24
A
1000-1298(2017)08-0026-07

