新型PURU+RR+S球面并联人形机器人踝关节机构动力学性能分析

徐奕柳 杨 龙 杨中原 肖 超 周玉林

1.北京卫星环境工程研究所，北京，100094 2.燕山大学机械工程学院，秦皇岛，0660043.石家庄铁道大学机械工程学院，石家庄，050043

新型PURU+RR+S球面并联人形机器人踝关节机构动力学性能分析

徐奕柳1杨 龙2,3杨中原2肖 超2周玉林2

1.北京卫星环境工程研究所，北京，100094 2.燕山大学机械工程学院，秦皇岛，0660043.石家庄铁道大学机械工程学院，石家庄，050043

提出了一种新型PURU+RR+S球面并联人形机器人踝关节机构，根据机构的几何约束关系和速度合成定理，建立包括各个构件位姿、速度的机构运动学模型。在此基础上，考虑各构件惯性力的影响，基于虚功原理和拉格朗日方程，建立了机构动力学模型。通过实验测量，得到一组人体踝关节的运动学数据，利用傅里叶公式进行拟合，得到人体踝关节的位姿函数。将此位姿函数分别作为理论模型、踝关节虚拟样机的输出，得到踝关节机构输入的数值解、仿真数据，验证了运动学和动力学模型的正确性。研究结果为该人形机器人踝关节机构在工程中的结构设计与应用提供了动力学理论基础和依据。

人形机器人；踝关节机构；动力学分析；球面并联机构

0 引言

仿生学在人形机器人关节设计中具有广阔的应用前景[1-3]，仿生踝关节是人形机器人机械本体的重要组成部分之一，得到众多学者的关注。

CECCARELLI等[4]以并联机构作为人形机器人的仿生关节构型，该构型从结构组成、运动特性上讲，更加符合人体客观实际。戚开诚[5]用两自由度球面并联机构UP+R作为人形机器人的踝关节。金振林等[6]以球面5R机构为原型，提出了一种机器人踝关节。俞志伟等[7]采用虎克铰链作为人形机器人踝关节。付金海[8]以十字万向节作为机器人的踝关节，两个驱动器结构为直流电机带动滚珠丝杠，驱动器与脚板通过球形关节连接，可实现脚板上下左右的运动。LOHMEIER等[9]以万向节作为人形机器人LOLA的踝关节研制了双足机器人。OGURA等[10]设计了人形机器人WABIAN-IIR，采用万向节作为踝关节，结构与LOLA类似，足部增加一个被动脚趾自由度，是现今走路最像人类的人形机器人。ALFAYAD等[11]设计了一种串并联相结合的三自由度混联踝关节。

机构的动力学模型是进行动力学性能评价、动力学控制研究的基础和前提。目前比较成熟的动力学建模方法有Lagrange法、牛顿-欧拉法、凯恩法、虚功原理法等。李成刚等[12]基于虚功原理推导了两自由度球面并联机构的动力学模型。WU等[13]以3-RRR球面并联机构为研究对象，采用Lagrange法建立了动力学模型并进行了结构优化设计。WANG等[14]以3-DOFs驱动冗余并联机器人为研究对象，在传统牛顿-欧拉法的基础上，提出一种简化的动力学建模方法。刘晓等[15]基于耦合并联机构特殊的运动特性，结合虚功率形式达朗贝尔原理建立了并联机构的耦合动力学模型。

现有的并联仿人机器人踝关节大都采用虎克铰作为核心机构，通过连杆并联驱动实现踝关节的俯仰和翻转运动，这类机构占用空间较大,仿生水平较低。

本文提出一种新型PURU+RR+S球面并联人形机器人踝关节机构，首先建立包括各个构件位姿、速度的完整运动学模型；其次，基于运动学模型，根据虚功原理和拉格朗日方程，建立机构的动力学模型；最后，利用人体踝关节运动数据，对机构运动学及动力学模型进行验证。

1 PURU+RR+S球面并联人形机器人踝关节机构

如图1所示，PURU+RR+S球面并联人形机器人踝关节机构由三个运动支链组成。

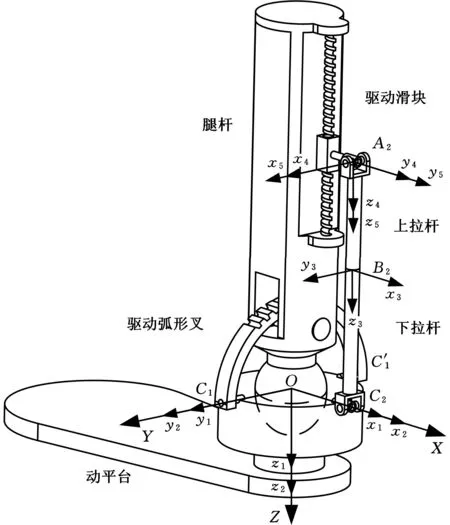
图1 PURU+RR+S球面并联人形机器人 踝关节机构Fig.1 PURU+RR+S spherical parallel humanoid ankle mechanism

支链2由机架、驱动滑块、上拉杆、下拉杆和动平台组成。上下拉杆通过转动副B2连接，转动副的轴线方向为沿上下拉杆的长度方向。上拉杆的上端、下拉杆下端分别通过U副A2、U副C2与驱动滑块、动平台相连接。在初始位姿时，驱动滑块的轴线和拉杆的轴线组成的平面垂直于弧形叉的平面。

支链3为机架和动平台组成的中心球面副支链。在驱动滑块和驱动弧形叉的驱动下，动平台可以实现两个方向的摆动。

以球心点O为坐标原点,建立与机架固连的固定坐标系{C}:OXYZ，其中，Z轴与机架轴线重合，指向竖直向下，Y轴与驱动弧形叉的转动副轴线重合，指向如图1所示，X轴由右手法则确定。

将动平台、弧形叉、下拉杆、上拉杆和驱动滑块分别记为构件i(i=1,2,3,4,5)，以O点为坐标原点,分别建立与构件1固连的坐标系{N1}:Ox1y1z1，与构件2固连的坐标系{N2}:Ox2y2z2。

以B2点为坐标原点,建立与构件3固连的坐标系{N3}:B2x3y3z3。以A2点为坐标原点,分别建立与构件4固连的坐标系{N4}:A2x4y4z4,与构件5固连的坐标系{N5}:A2x5y5z5。初始时刻，5个坐标系与固定坐标系的对应坐标轴正向平行。

初始位姿时，A2点和C2点在固定坐标系{C}中的坐标为：

CA2=(r，0，L)CC2=(r，0，0)

其中，r和L为相应的坐标值。

2 机构的运动学模型

2.1 位置反解

机构的输入记为(α,l)，其中，α为驱动弧形叉绕X轴转动的角度，l为驱动滑块沿Z轴方向的位移。输出记为(θx,θy)，其中，θx、θy分别为动平台绕x1、y1轴转动的角度。坐标系{N1}相对于固定坐标系{C}的旋转矩阵为

(1)

式中，cθx表示cosθx,sθx表示sinθx，其余类似。

此时，C2点在固定坐标系{C}中的坐标为

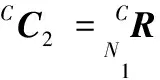
(2)

A2点在固定坐标系{C}中的坐标为

CA2=(r，0，L+l)

(3)

根据杆长约束方程和机构运动特性，得到

(4)

2.2 各构件的姿态

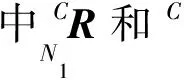
由机构的运动特性，得到

(5)

(6)

根据几何关系约束方程，得到

(7)

A3=su2sθyc(u1-θx)+cu2cθy

由于滑块相对于固定坐标系的姿态不变，上拉杆坐标系{N4}相对于固定坐标系{C}的旋转矩阵为

(8)

下拉杆坐标系{N3}相对于固定坐标系{C}的旋转矩阵为

(9)

2.3 各构件的角速度

由角速度合成定理可知，构件i的角速度矢量为

ωi=Ei×ωhi

(10)

式中，Ei为构件i的姿态角一阶导数矢量ωhi变换到角速度矢量ωi的变换矩阵。

(11)

(12)

(13)

(14)

其中，u3x、u3y由机构的尺寸参数、位姿参数确定。

2.4 各构件质心的位置和线速度

构件i(i=1,2,3,4,5)的质心记为ri，ri在坐标系{Ni}中的位置矢量Niri由单个构件的尺寸确定，ri在固定坐标系{C}中的位置矢量Cri为

(15)

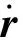
3 机构的动力学模型

PURU+RR+S球面并联人形机器人踝关节机构为过约束机构，采用虚功原理和拉格朗日方程相结合的方法，从能量角度出发，分析系统的动能、势能和广义力，推导出基于任务空间的动力学方程，避开讨论冗余约束对动力学模型的影响。

为便于分析，选择动平台的姿态角作为广义坐标，忽略各运动副质量和摩擦力的影响，假设各构件的质量均匀分布，各关节的约束力为理想约束。

3.1 系统动能

机构的动能为5个构件动能的总和，表示为

(16)

式中，mi为构件i的质量；Ipi为构件i的转动惯量矩阵。

Ipi由下式确定:

(17)

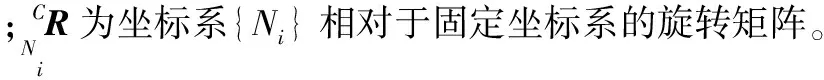
3.2 系统势能

势能的大小与零点位置的选择有关，设固定坐标系的原点为零势能点，不计构件弹性和摩擦，则系统的势能为

(18)

式中，g为重力加速度；zti、z0i分别为运动状态、初始状态时，构件i质心在Z轴方向的投影。

3.3 动力学方程

根据虚功原理，驱动力的虚功之和等于广义力载荷的虚功之和，得到

(19)

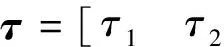
将式(16)、式(18)、式(19)代入拉格朗日方程，得到

(20)

化简求得驱动力为

(21)

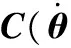
4 仿生数值计算与仿真

4.1 人体踝关节的运动数据

使用Xsens MVN惯性运动捕捉系统测量人体踝关节的运动数据，即实验对象以1.2 m/s的速度行走时，踝关节两个方向的摆动角度。

实验环境为常温，无强磁干扰。实验对象为10名男性(编号：01～10)和10名女性(编号：11～20)，男性实验对象身高、体重为(1.710±0.030)m、(68±2.5)kg，女性实验对象身高、体重为(1.572±0.028)m、(45±2.1)kg。

人体踝关节的俯仰角度θx随时间的变化规律如图2所示，对测量得到的数据进行拟合，得到俯仰角度θx随时间变化的拟合函数:

θx=-0.044-0.102cos(5.284t)+0.004sin(5.284t)-0.022cos(10.568t)+0.066sin(10.568t)

(22)

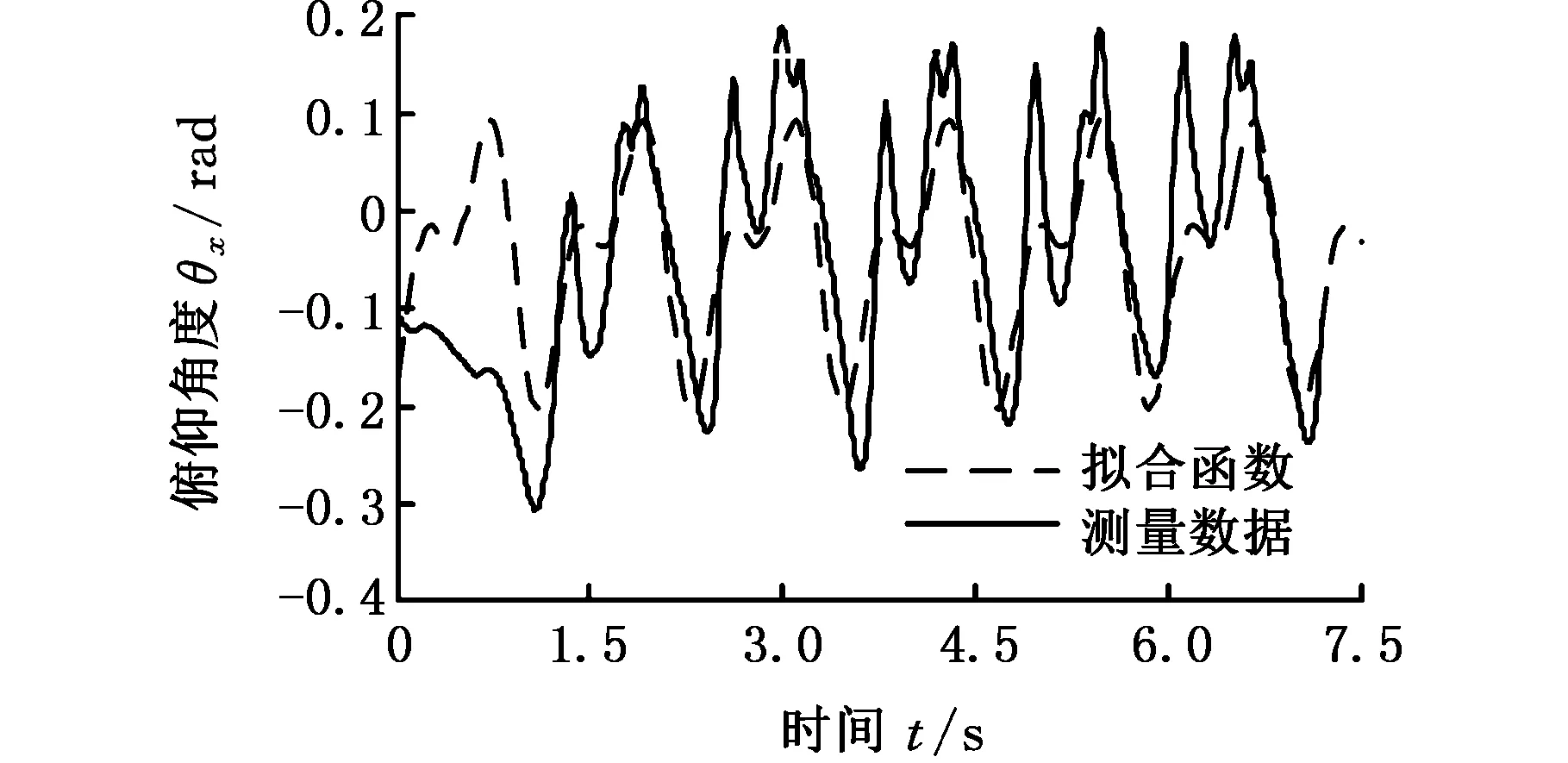
图2 人体踝关节的俯仰角度Fig.2 Pitch angle of human ankle

人体踝关节的横滚角度θy随时间的变化规律如图3所示，对测量得到的数据进行拟合，得到横滚角度θy随时间变化的拟合函数:

θy=-0.035-0.058cos(5.305t)-0.073sin(5.305t)+0.1cos(10.610t)+0.009sin(10.610t)

(23)

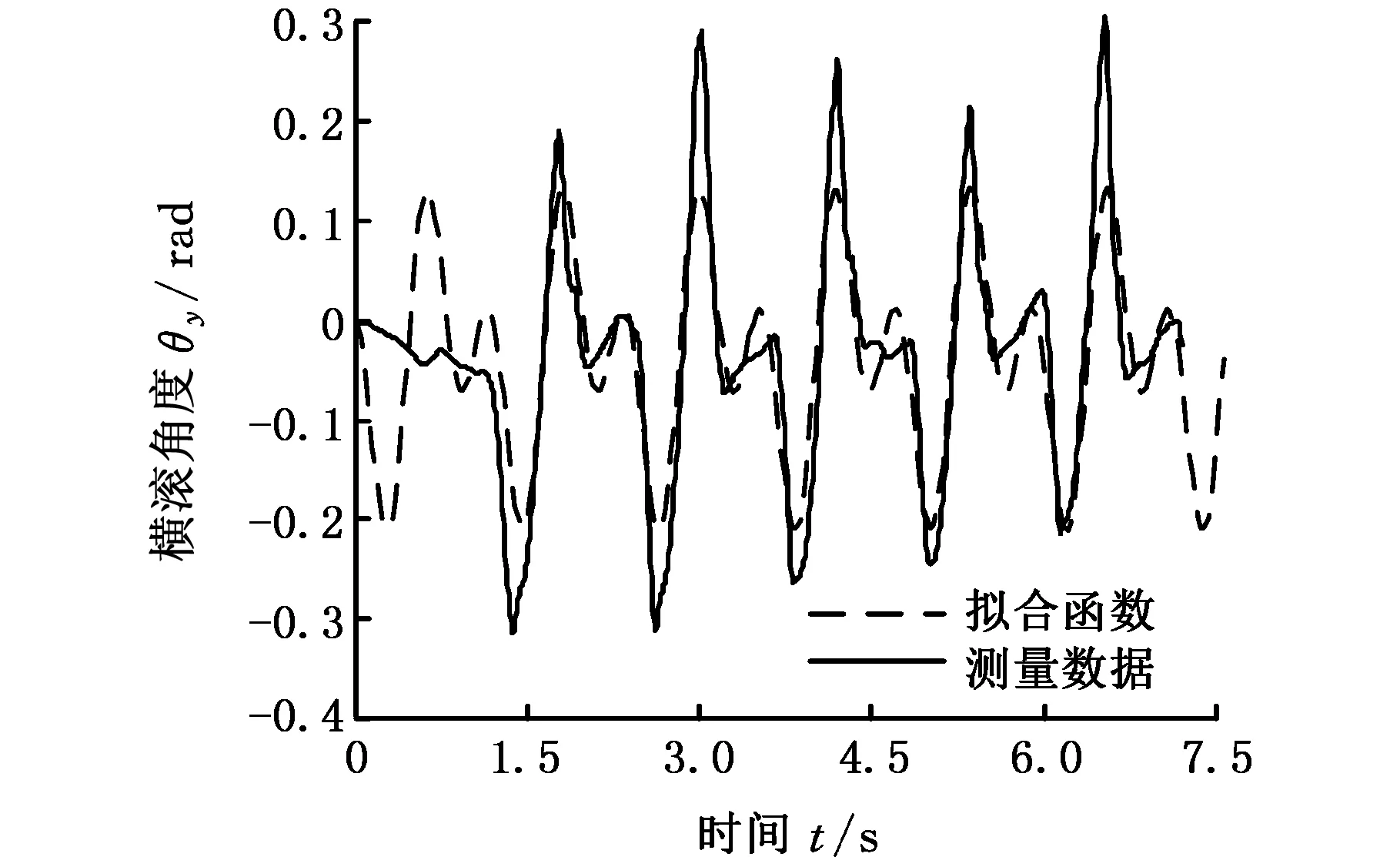
图3 人体踝关节的横滚角度Fig.3 Roll angle of human ankle

4.2 运动学数值计算与仿真

将人体踝关节运动学拟合函数即式(22)、式(23)分别代入式(11)、式(15)，可得到动平台角速度、动平台质心线速度的数值解，见图4、图5。

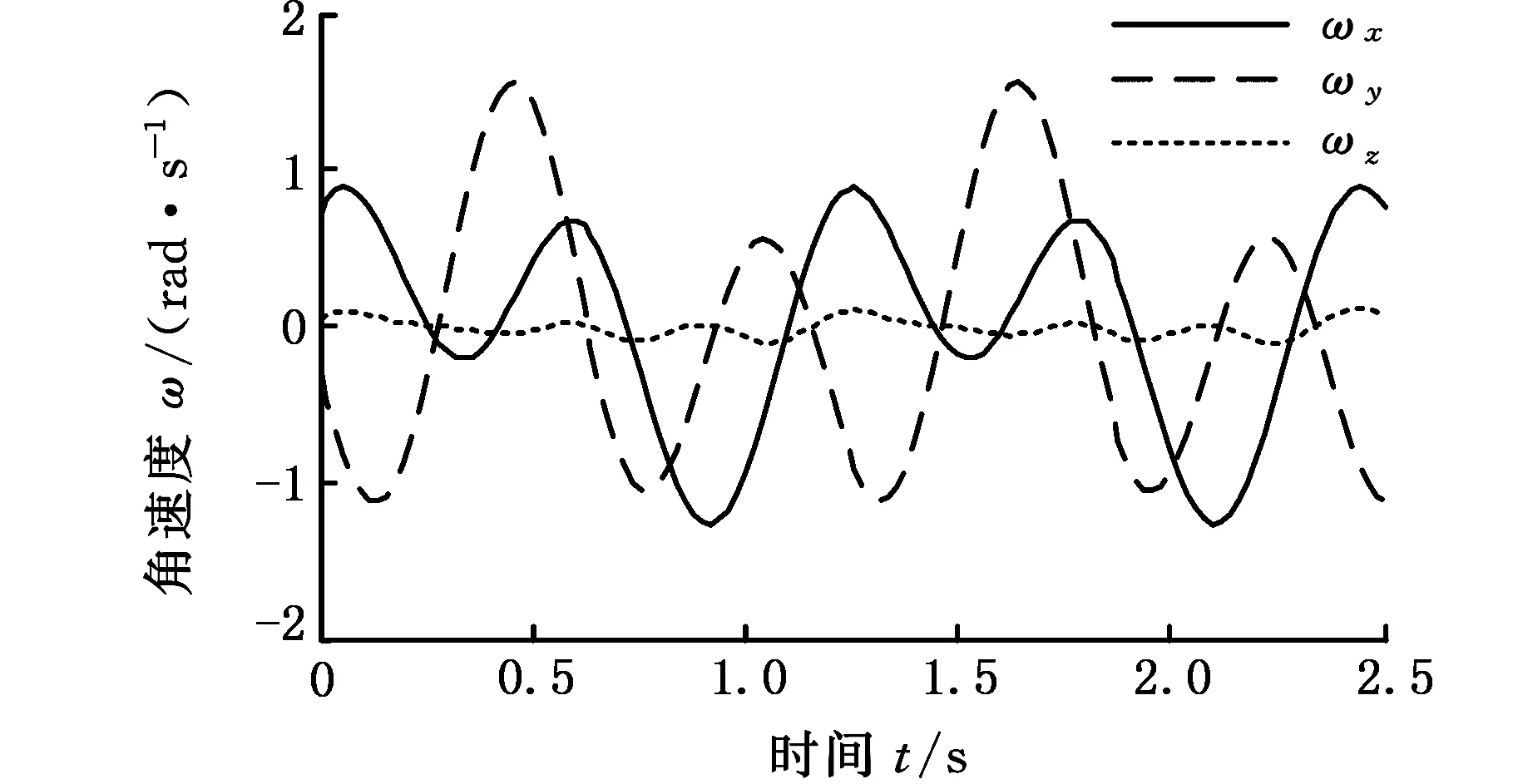
图4 动平台角速度的数值解Fig.4 Numerical solution of angular velocity of moving platform

图5 动平台质心线速度的数值解Fig.5 Numerical solution of centroid linear velocity of moving platform

将人体踝关节运动学拟合函数，即式(22)、式(23)作为踝关节机构虚拟样机的输出，通过ADAMS软件，得到动平台角速度、动平台质心线速度的仿真数据，如图6、图7所示。

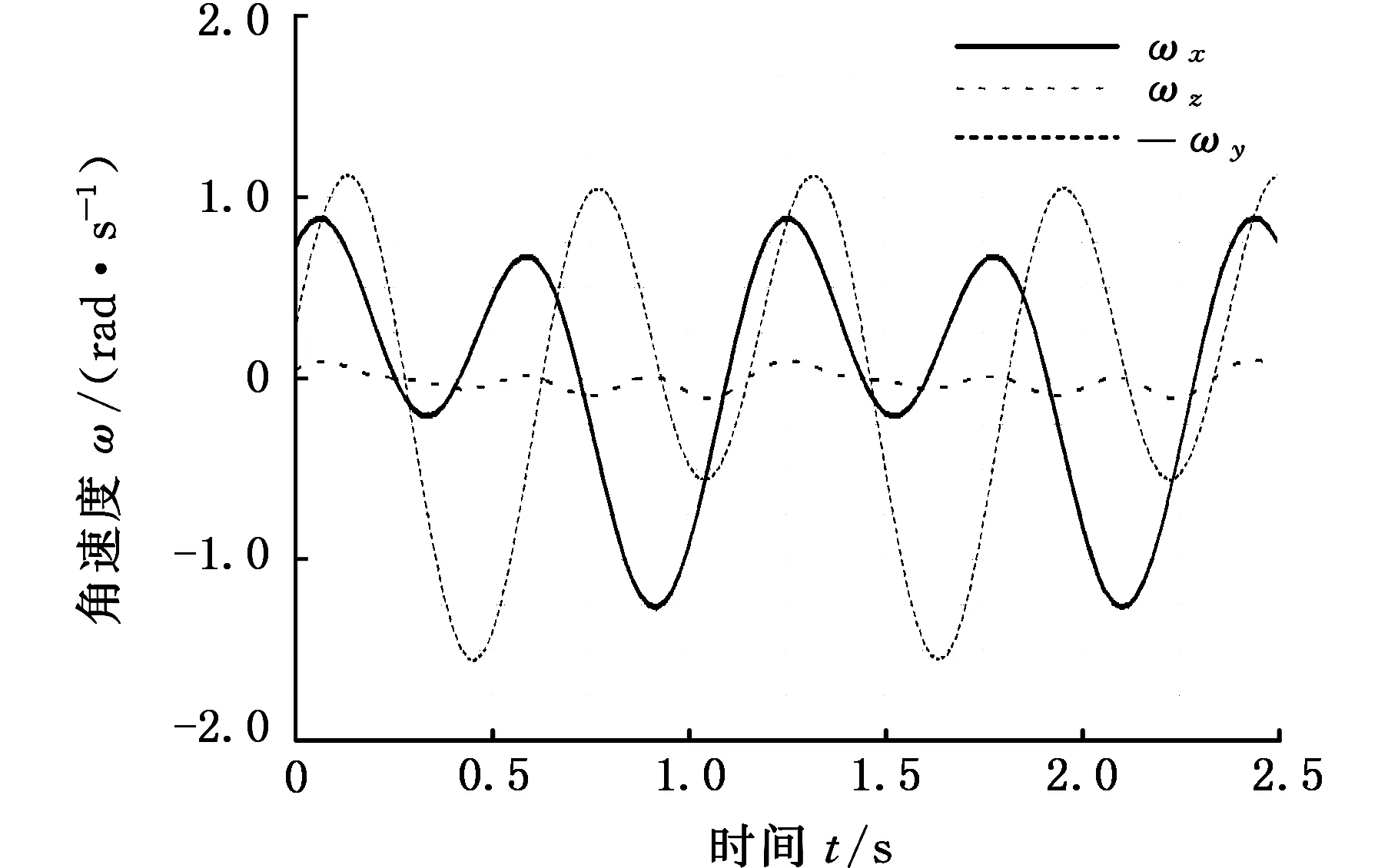
图6 动平台角速度仿真数据Fig.6 Simulation data of angular velocity of moving platform

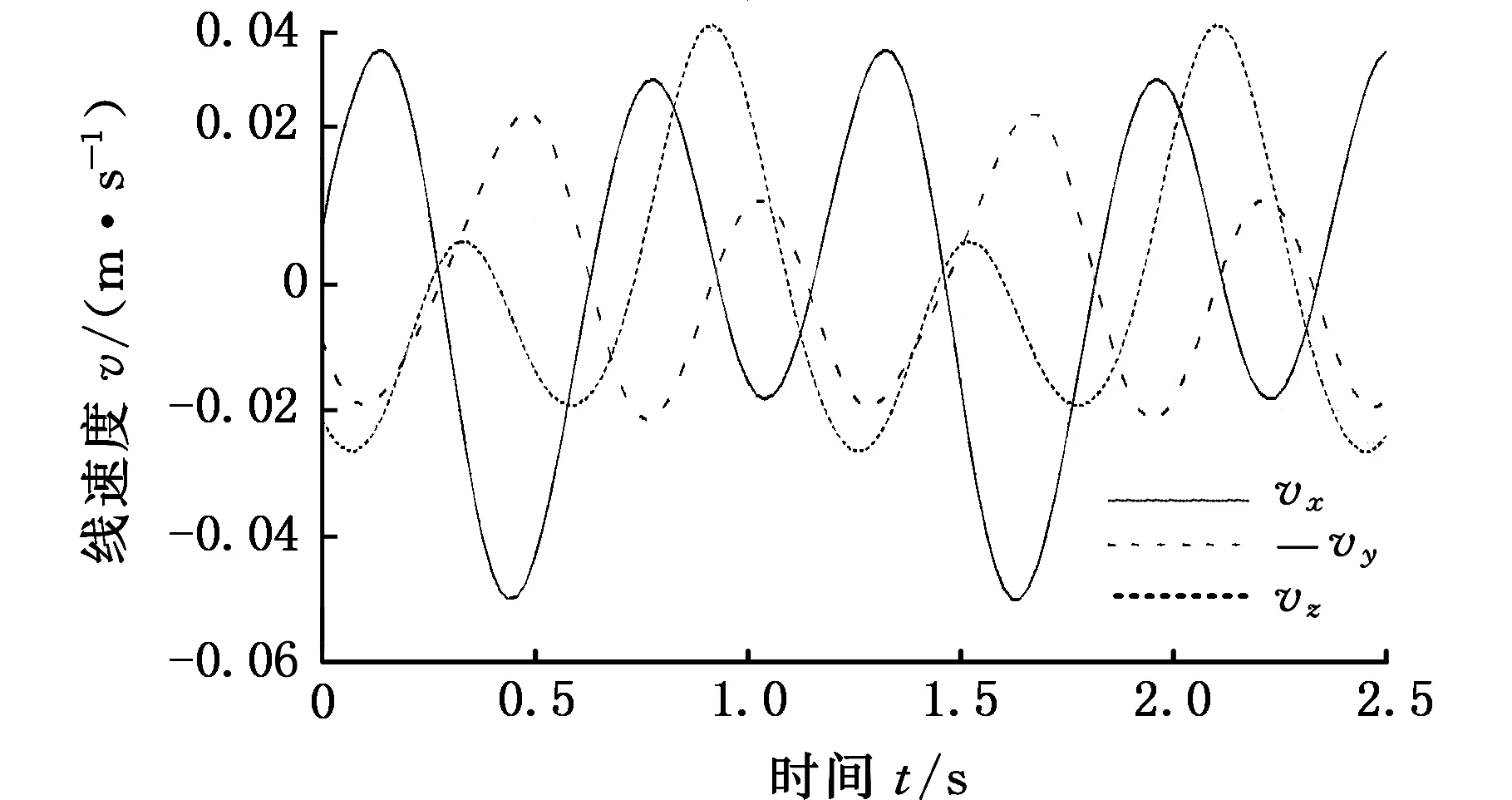
图7 动平台质心线速度的仿真数据Fig.7 Simulation data of centroid linear velocity of moving platform

对比分析发现，理论计算结果与仿真结果基本一致，证明踝关节机构运动学模型的正确性。

4.3 动力学数值计算与仿真

将人体踝关节运动学拟合函数，即式(22)、式(23)代入式(21)，得到驱动力和驱动力矩的数值解，如图8所示。

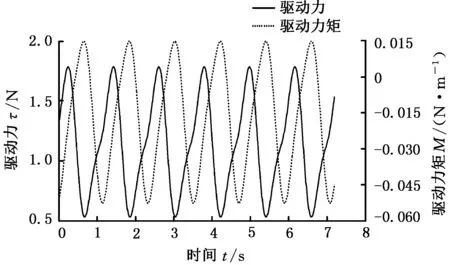
图8 驱动力/力矩的数值解Fig.8 Numerical solution of driving force/torque

将人体踝关节运动学拟合函数，即式(22)、式(23)作为踝关节机构虚拟样机的输出，通过ADAMS软件，得到驱动力和驱动力矩的仿真数据，如图9所示。

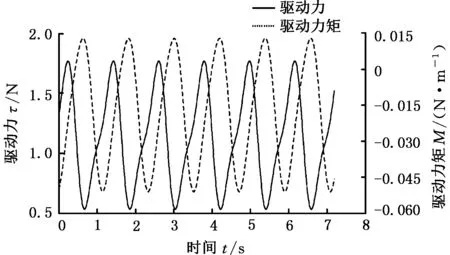
图9 驱动力/力矩的仿真数据Fig.9 Simulation data of driving force/torque

对比分析发现，理论计算结果与仿真结果基本一致，证明踝关节机构动力学模型的正确性。

5 结论

(1)本文提出了一种PURU+RR+S球面并联人形机器人踝关节机构，建立了包括各个构件位姿、角速度的完整运动学模型。

(2)在运动学模型的基础上，采用虚功原理和拉格朗日方程相结合的方法，推导出机构基于任务空间的动力学方程。

(3)通过实验测量，得到一组人体踝关节的运动学数据，利用此数据，通过数值计算和仿真，验证了运动学、动力学模型的正确性。

[1] XING Denghai, CHEN Wuyi, ZHAO Ling, et al. Structural Bionic Design for High-speed Machine Tool Working Table Based on Distribution Rules of Leaf Veins[J]. Science China Technological Science, 2012, 55(8): 2091-2098.

[2] JIA Honglei, LI Changying, ZHANG Zhihong, et al. Design of Bionic Saw Blade for Corm Stalk Cutting[J]. Journal of Bionic Engineering, 2014, 11(1): 90-97.

[3] CHEN Jie, LIU Yubin, ZHAO Jie, et al. Biomimetic Design and Optimal Swing of a Hexapod Robot Leg[J]. Journal of Bionic Engineering, 2014, 11(1): 26-35.

[4] CECCARELLI M, CARBONE G. A Stiffness Analysis for CaPaMan (Cassino Parallel Manipulator)[J]. Mechanism and Machine Theory, 2002, 37(5): 427-439.

[5] 戚开诚. 仿人形机器人机构设计[D]. 天津：河北工业大学, 2004. QI Kaicheng. The Mechanic Design of the Humanoid Robot[D]. Tianjin:Hebei University of Technology, 2004.

[6] 金振林,高峰. 机器人的踝关节: 中国, 200710139498X [P]. 2007-09-22. JIN Zhenlin, GAO Feng. Ankle Joint of Robot: China, 200710139498X [P]. 2007-09-22.

[7] 俞志伟, 王立权. 双足机器人并联踝关节优化设计[J].机械工程学报, 2009, 45(11): 52-57. YU Zhiwei, WANG Liquan. Optimal Design for Biped Robot Parallel Ankle Joint[J]. Journal of Mechanical Engineering, 2009, 45(11): 52-57.

[8] 付金海. 仿人机器人机构设计与步行仿真[D]. 沈阳：东北大学,2010. FU Jinhai. Mechanical Design and Walking Simulation of Humanoid Robot[D]. Shenyang：Northeast University,2010.

[9] LOHMEIER S, BUSCHMANN T, SCHWIENBACHER M, et al. Leg Design for a Humanoid Walking Robot[C]// IEEE-RAS International Conference on Humanoid Robots. Pittsburgh, 2007: 536-541.

[10] OGURA Y, SHIMOMURA K, KONDO H, et al. Human-like Walking with Knee Stretched, Heel-contact and Toe-off Motion by a Humanoid Robot[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing, 2006: 3976-3981.

[11] ALFAYAD S, OUEZDOU F B, NAMOUN F. New Three DOF Ankle Mechanism for Humanoid Robotic Application: Modeling, Design and Realization[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. St Louis, MO, 2009: 4969-4976.

[12] 李成刚, 吴洪涛, 朱剑英. 球面并联机构动力学模型构成项对比研究[J].机械科学与技术, 2011, 30(5):807-812. LI Chenggang, WU Hongtao, ZHU Jianying. A Contrastive Study of the Items of Dynamics Model of the Spherical Parallel Mechanism[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(5): 807-812.

[13] WU G L, STÉPHANE C, BAI S P, et al. Dynamic Modeling and Design Optimization of a 3-DOF Spherical Parallel Manipulator[J]. Robotics and Autonomous Systems, 2014, 62(10): 1377-1386.

[14] WANG L P, WU J, WANG J S. Dynamic Formulation of a Planar 3-DOF Parallel Manipulator with Actuation Redundancy[J]. Robotics and Computer Integrated Manufacturing, 2010, 26(1): 67-73.

[15] 刘晓, 赵铁石, 边辉, 等.耦合型3自由度并联稳定平台机构动力学分析[J]. 机械工程学报, 2013, 49(1): 45-52. LIU Xiao, ZHAO Tieshi, BIAN Hui, et al. Dynamics Analysis of a 3-DOF Coupling Parallel Mechanism for Stabilized Platform[J]. Journal of Mechanical Engineering, 2013, 49(1): 45-52.

(编辑 王旻玥)

Dynamics Property Analyses of a Novel PURU+RR+S Spherical Parallel Humanoid Robotic>Ankle Mechanisms

XU Yiliu1YANG Long2,3YANG Zhongyuan2XIAO Chao2ZHOU Yulin2

1.Beijing Institute of Spacecraft Environment Engineering，Beijing，1000942.School of Mechanical Engineering,Yanshan University，Qinhuangdao，Hebei,0660043.School of Mechanical Engineering,Shijiazhuang Tiedao University,Shijiazhuang,050043

A novel PURU+RR+S spherical parallel humanoid robotic ankle mechanism was proposed herein, the kinematic models including poses, velocities of all components were established according to geometric constraint relations and velocity composition theorem of this mechanism. Based on this, the influences of inertia forces of each components were considered, dynamics model of this mechanism was established based on the principles of virtual work and Lagrange equation. A group of kinematic data of human ankles were obtained by experimental measurements, position and orientation functions of human ankles were derived using Fourier formula. The position function was used as outputs of the theoretical model and the virtual prototype of ankle mechanisms respectively. Numerical solutions and simulation data of the inputs of ankle mechanisms were obtained, and then the correctnesses of kinematic and dynamic models were confirmed. The research provides a theoretical basis of dynamics for structure design and applications of the humanoid robotic ankle mechanisms in engineering.

humanoid robot; ankle mechanism; dynamics analysis; spherical parallel mechanism

2016-09-08

国家自然科学基金资助项目(51275443)

TP24

10.3969/j.issn.1004-132X.2017.16.012

徐奕柳，女，1985年生。北京卫星环境工程研究所高级工程师。主要研究方向为航天器总体装配、工艺装备设计。杨 龙，男，1988年生。燕山大学机械工程学院博士，石家庄铁道大学机械工程学院讲师。杨中原，男，1992年生。燕山大学机械工程学院硕士研究生。肖 超，女，1990年生。燕山大学机械工程学院硕士研究生。周玉林(通信作者)，男，1961年生。燕山大学机械工程学院教授、博士研究生导师。E-mail：zyl@ysu.edu.cn。