基于标准序列浮动前向特征选择的改进算法研究
周 阳, 周 炎,周 桃,任 卉,石玲玲
(北京宇航系统工程研究所,北京 100076 )
基于标准序列浮动前向特征选择的改进算法研究
周 阳, 周 炎,周 桃,任 卉,石玲玲
(北京宇航系统工程研究所,北京 100076 )
信息技术的高速发展促进了信息领域内涵的根本性变革,信息特征的表述方法和内涵不断扩充,高维特征大幅涌现;这些高维特征中可能存在许多不相关和冗余特征,造成了维度灾难,这对基于特征空间聚散特性的分类识别算法提出了更高的要求,需要利用特征选择算法,降低特征向量维数并消除数据噪音的干扰;针对高维特征向量引入的维度灾难等问题,围绕目标分类识别的具体应用,基于标准的序列浮动前向特征选择算法,完成交叉验证重复次数优化,提出了改进的特征选择算法;通过仿真实验表明,基于Bayesian分类器开展识别时,改进算法能够在确保分类识别正确率的前提下,有效提升特征选择的计算速度,并维持一个相对更为收敛且稳定的置信区间,具备良好的准确度。
特征选择;浮动前向选择;Bayesian分类器;目标识别
0 引言
对于典型的模式分类问题来说,决定样本属于某一类通常由描述样本的特征向量决定,即所有的样本被抽象为一组特征向量,特征向量在特征空间的可分性直接决定了分类器性能的优劣[1]。信息技术的飞速发展引发了信息领域内涵的极大延伸,各类特征提取算法不断涌现,一方面表征人们对于事物的认识角度得到扩展,另一方面则形成了大量的高维特征数据,这对于分类问题提出了诸多挑战,如冗余特征信息带来的计算资源浪费、非预期信息引发的分类器性能降低以及维度灾难等,这需要在不降低或有限降低分类器性能的基础上,提出必要的特征降维方法,确保分类算法的计算效率和实时性指标。
特征选择是一种典型的特征向量降维方法,其能够从全维度的特征集合中,基于特定的规则和策略,选取部分特征构成一个低维度的特征子集,用于完成后续的分类问题研究。优秀的特征选择方法在能够充分表征该类别既有特征的前提下,能够有效移除冗余特征和非相关特征,从而降低特征向量维数,改善范磊性能并提高运算效率[2]。
本文主要基于标准序列浮动前向特征选择算法(sequential floating forward selection,SFFS),围绕算法效率和处理速度提出了一种改进算法,并针对Bayesian分类器的目标识别问题,选择四类船舶目标的红外图像,完成了实验仿真分析,通过仿真结果表明,改进SFFS算法能够在有效确保识别准确率的同时,有效提升了特征选择计算速率。
1 特征与特征选择
1.1 特征
特征是某一类事物区分于其他事物的一次提取或多次提取的信息,或是这些提取信息的集合。在面向具体应用问题中,需要根据实际需求选择合适的特征提取方法并抽取合适的特征来表述事物本质信息,依靠人工经验的方法是主观的,不科学的,也是不可取的[3]。
一般来说,面向图像目标识别应用的特征提取过程中应满足的3个基本原则:
1) 特征的稳定性,指特征应具备与噪声和非相关信息的不敏感特性;
2) 特征的易算性,指特征或特征向量应易于提取和分类计算;
3) 特征的类间可区分性,指图像中不同类别目标的特征向量距离越大越好,同类目标的特征向量距离越小越好,即具有较小的类内距离和较大的类间距离。
1.2 特征选择
在图像目标识别的具体应用问题中,特征提取方法成千上万,形成的目标特征是一个较高维度的向量,但是高维度的特征空间使得识别问题计算复杂度增高,而部分非相关或非预期特征信息会导致识别率降低。
在目标识别的实际应用中,在完成特征提取后往往会形成较高维度的特征向量,但是过多的特征量会使得计算复杂度增高,同时维数过高的特征向量对于目标识别率会造成负面效果。对于一个具体的分类识别计算模型来说,一般存在一个最大的特征维数,若实际的特征向量维数超过该值时,分类器不仅无法得到分类性能的改善和提高,而且由于高维数据的维度灾难和无法预测的特征间耦合关系,将会导致分类器的性能退化现象。因此在具体的目标识别和分类问题中,针对高维度特征向量进行降维是极为必要的,选择对于识别贡献率高的特征信息,而去除冗余甚至负影响的特征信息。
特征降维方法主要包括特征选择、特征变换等方法。其中特征变换是通过相应的映射关系,将高维特征向量变换为一个低维度的特征向量,从而实现特征降维。而特征选择则是从特征全集中,利用一定的规则和策略,选取部分特征构成一个新的特征空间,并完成后续的分类问题。
特征选择方法的数学表征可由如下公式表示。
(1)
特征选择策略大致可分为两类,即基于搜索及基于评价策略具体如图1所示[4]。
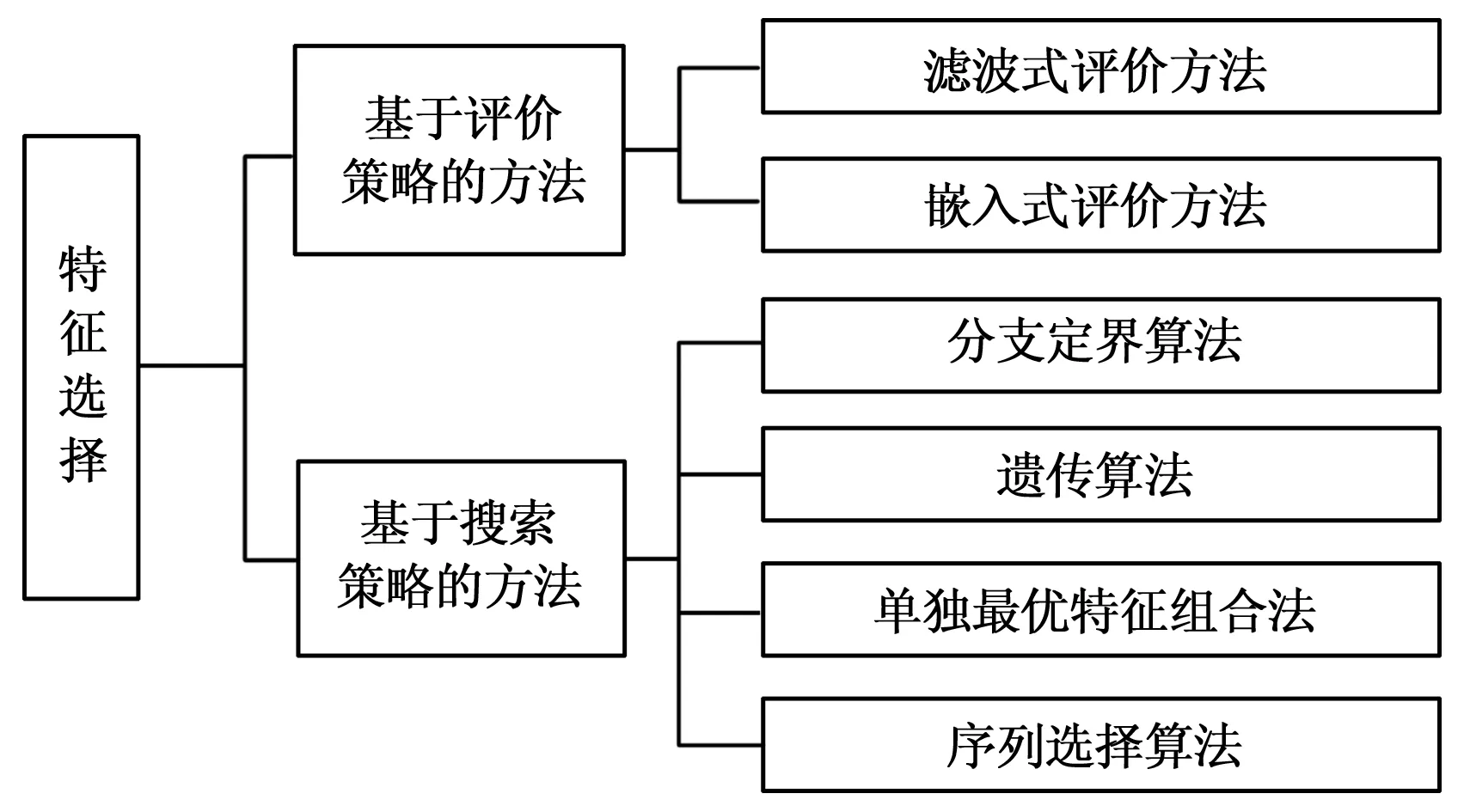
图1 特征选择方法分类图
基于搜索策略的特征选择方法主要通过依据给定评价标准,重点强调利用具体的搜索策略从特征全集中选择出一个合适的特征子集,典型方法包括分支定界算法[5]、遗传算法[6]、单独最优特征组合方法[7]及序列选择方法[8]等。
基于评价策略的特征选择方法主要关注特征集合的评价策略,如基于滤波式评价策略[9]能够有效滤除非相关的噪声信息,但是无法保证较小特征子集的局部最优。
2 标准序列浮动前向特征选择算法
标准序列浮动前向特征选择算法(sequential floating forward selection,SFFS)是一种典型的基于搜索策略的特征选择方法,主要包括两个步骤。
1)前向操作
即插入步骤,建立一个特征集合(起始时为空集),每次搜索时基于特定规则从特征全集中选择一个特征添加到该集合中。
在进行前向操作中,核心就是从候选特征全集中寻找一个特征,使得这个特征加入已选择特征子集后,已选择特征集合的分类正确率最大。
2)返向操作
即删除步骤,从已选特征集合中择取一个特征,若该特征同时满足去除该特征后,基于已选特征集合的分类正确率达到最大且大于去除前的条件时,从已选特征集合中删除该特征。在完成删除操作时,为避免得到局部最优解,因此需要根据具体情况决定是否执行删除处理。
标准SFFS算法的具体流程如图2所示。

图2 标准SFFS算法流程示意图
标准SFFS算法的一个优势就是能够在一定程度上规避特征集合的局部最优问题,而是选择出一个最优特征子集,作为分类器的分类输入。
3 基于改进SFFS的特征选择方法
3.1 基于分类正确率的评价判据
为验证改进SFFS算法的特征选择性能,本节基于Bayesian原理完成分类器设计,其分类正确率作为性能评估依据。
假定共有图像样本X个,表示为Pi,其中i=1,2,...,X,共提取Y维目标特征向量,特征全集表示为W={ωy},y=1,2,...,Y,可把全部图像样本按交叉验证折数S归为两类。
1)训练样本集:
在所有图像样本中选取一定的样本构建训练集Ptr,个数为Xtr,其所有目标分类情况均为已知,用于训练Bayesian分类器。
2)测试样本集:
将图像样本中未归为训练样本的全部图像用于构建测试样本集Pte,其样本个数为Xte,Xte=X-Xtr。测试样本集中目标分类情况为未知,需要基于选择的特征子集和Bayesian分类器进行目标识别归类,其分类正确率用于评估改进SFFS算法的选择性能。
一般来说,所有训练样本中的目标类别判定结果服从等概率分布,则当给定目标类别时,测试训练集Pte的特征向量是一个分类条件概率密度函数,其服从多元高斯分布,期望向量和协方差矩阵可基于样本期望向量和离散矩阵完成计算。该分类条件概率密度函数可用一个多元高斯函数进行建模,其中的均值向量和协方差矩阵可分别通过计算样本均值向量和样本离散矩阵来得到估计值[10]。
令C是一个非0即1的开关量,表示使用已选择特征集合对所有样本进行分类时,当分类正确时将C值置为1,否则为0。已选择特征集合的分类正确率用CA表示,其初始时为0,具体可由下式表示:
(2)
分类正确率等于各测试样本中基于特征子集的分类正确率总和,假定总重复次数为Q,第q次重复验证中,分类正确率的估计可表示为:
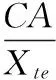
(3)
其期望如下式所示:
(4)
3.2 基于标准SFFS的改进算法
标准SFFS算法能够在一定程度上避免局部最优的问题,但是由于其需要针对每一个特征进行多轮次验证,算法的计算量较大,在面对一些具体应用时,其算法的实时性无法得到保证。本节主要从标准SFFS算法的前向操作入手,在进行重复验证时,首先判定该特征的类间区分能力,并依据其类间区分能力决定其重复验证次数,能够有效提升计算效率,加快算法收敛时间。
利用Tn表示算法选择的特征集合,在算法起始时,Tn为一个空集,其中n代表插入和删除的操作次数,即n=0时,Tn=Φ。假定共有样本m个,表示为Pi,i=1,2,...,m,训练样本经特征提取后形成了特征全集。
改进SFFS算法同样包含前向和返向两个步骤。
1)前向操作。
当首次进行前向和返向操作时,即n=0,在特征全集W={ωy} (y=1,2,...,Y)中按标准SFFS算法选取特征ω+,若此时:
ω+=argmaxCA(PT0+ω+)
(5)
则表明ω+为此轮插入操作中的最优特征,则:
T1=T0∪ω+
(6)
当n>0执行前向操作时,首先判定择取特征与已选特征集合关联性情况,并依据具体关联程度设定重复次数,从而减少低贡献度特征的重复计算次数,提升运行效率。
假定择取特征为ωy,已选特征集合为Tn,那么择取特征ωy与已选特征集合Tn间关联性表示为:

(7)
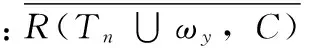
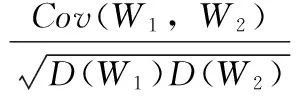
(8)
W1,W2分别表示特征ω1,ω2在样本空间的表征向量,Cov表示协方差计算,D表示方差计算。
择取特征的重复次数需要依据具体的分类应用确定,如设定关联性程度门限为G,超过该门限时进行足额的重复验证,未超过时可视情见啥重复次数,也可分级设定多个关联性程度门限,并在各级内执行不同的重复次数缩减制度,从而在整体上减少对于择取特征的交叉验证重复次数。
2)返向操作。
删除步骤,即满足特定条件时,从已选特征集合中删除一个特征。在完成删除操作时,为避免得到局部最优解,因此需要根据具体情况决定是否执行删除处理。
在执行第n次插入或删除操作时,假定有ω-∈Tn,并判定是否对其执行删除操作。首先计算去除该特征后,选特征集合Tn-ω-的关联性程度,并设定相应门限,评估交叉验证重复次数。
设定该特征重复次数后,若该特征同时满足:
ω-=argmaxCA(PTn-ω-)
(9)
CA(PTn-ω-)>CA(PTn)
(10)
即判定在选择特征集合中删除特征ω-,若没有满足条件的特征,则返回插入操作步骤。
3)特征输出。
在完成N次插入和删除操作后,若再无满足条件的插入特征和删除特征,则算法收敛并结束。此时对应的已选择特征集合为TN,即为最优特征子集,其对应的分类正确率为CA(PTN)。
4 实验结果及分析
4.1 实验图像及特征提取
实验选取四类船舶目标的红外目标来进行改进SFFS算法性能验证,具体如图3所示。通过对4幅红外图像进行平移变换、角度变换、尺度变换,每类目标生成500幅图像样本,共计产生2 000副图像样本。

图3 船舶目标仿真实验图像
对于每个红外船舶图像样本,分别提取15种特征构成的74维目标特征向量,从而构建出一个特征矩阵数据库,用来进行特征选择和分类识别[11-15]。

图4 实验图像目标特征向量
4.2 标准SFFS与改进SFFS的特征选择方法比较实验
实验中,设置折数S=15,最大重复次数Q=100,各特征的重复次数与关联性分析结果成正比关系。
如表1所示,分别给出了标准SFFS及改进SFFS的特征选择方法的运行时间,可以发现改进SFFS算法耗时明显少于标准SFFS算法,这是由于在进行交叉验证时,首先基于择取特征的关联性程度分析优化了交叉验证重复次数,有效提升了算法收敛时间,实现了算法效率的改进。

表1 运行时间比较表
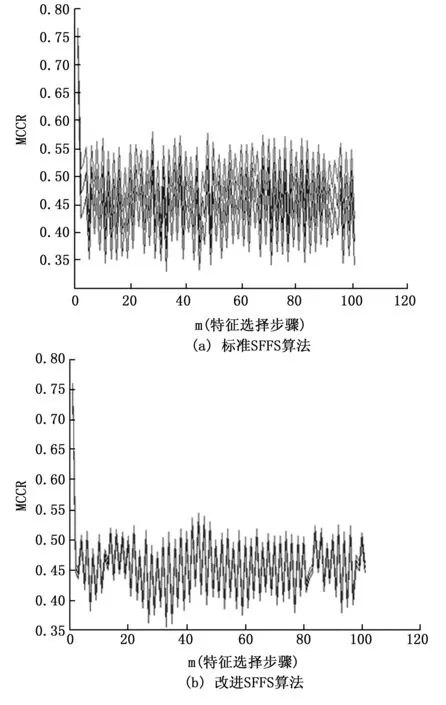
图5 MCCR和置信区间比较
图5则给出了标准SFFS算法及改进SFFS算法的平均分类识别率及其置信区间对于特征选择步骤数的曲线图。由图可见,本文提出的改进SFFS算法在提升计算效率的情况下,相比于标准SFFS算法,其平均分类识别率指标并未下降甚至略有提升,同时图5(b)中平均分类识别率的置信区间的宽度窄且较为固定,这表明其收敛程度更好,置信度更加稳定。
5 结论
本文主要基于高维特征涌现引入的诸多数据处理困难,基于标准序列浮动前向特征选择算法,围绕计算速度和准确度两个方面,提出了一种改进方法,并通过仿真实验表明,改进SFFS算法在一定程度上能够有效提升特征选择的计算速度,并随着特征选择步骤的增加,能够维持一个相对更为收敛且稳定的置信区间,具备良好的准确度。
[1]王 飞. 模式分类中混合特征选择方法研究[D].兰州:兰州大学,2015.
[2]田旷.面向高位数据的特征选择算法研究[D].北京 : 北京交通大学,2012.
[3]荣盘祥,曾凡永,黄金杰.数据挖掘中特征 选择算法研究[J].哈尔滨理工大学学报,2016,21(1) :106-109
[4]Sun Z, G.Bebis, R.Miller. Object detection using feature subset selection [J]. Pattern recognition, 2004, 37(11): 2165-2176.
[5]Hamamoto Y, Uchimura S, Matsuura Y, et al. Evaluation of the branch and bound algorithm for feature selection[J]. Pattern Recognition Letters, 1990, 11(7): 453-456.
[6]Siedlecki W, Sklansky J. A note on genetic algorithms for large-scale feature selection[J]. Pattern Recognition Letters, 1989, 10(5): 335-347.
[7]边肇祺, 张学工. 模式识别[M]. 北京: 清华大学出版社, 2000.
[8]Mao K Z. Fast orthogonal forward selection algorithm for feature subset selection[J]. Neural Networks, 2002, 13(5): 1218-1224.
[9]Zhou X, Wang X, R.D.Edward. Nonlinear probit gene classification using mutual information and wavelet-based feature selection[J]. Biological Systems, 2004, 12(3): 371-386.
[10]Tao C, Jin H. Max-margin based Bayesian classifier[J]. Frontiers of Information Technology&Electronic Engineering, 2016, 17(10):973-981.
[11]孙君顶, 赵珊. 图像低层特征提取与检索技 术[M]. 北京: 电子工业出版社, 2009.
[12]Freeman H. Shape description via the use of critical points[J]. Pattern recognition, 1978, 10(3): 159-166.
[13]He X C, Yung N. Curvature scale space corner detector with adaptive threshold and dynamic region of support[C]. Hong Kong, China: Proceedings of IEEE International Conference on Pattern Recognition, 2004: 791-794.
[14]Chen C C. Improved moment invariants for shape discrimination[J]. Pattern recognition, 1993, 26(5): 683-686.
[15]Gupta L, Srinath MD. Contour sequence moments for the classification of closed planar shapes[J]. Pattern recognition, 1987, 20(3): 267-272.
Research on Improved Algorithm Based on The Sequential Floating Forward Selection
Zhou Yang,Zhou Yan,Zhou Tao,Ren Hui, Shi Lingling
(Beijing Institute of Astronautical System Engineering,Beijing 100076, China)
With the rapid development of information technology, the indicative method on the information characteristics keep expanding,high-dimensional feature emerge and grow with a massive trend. These high-dimensional feature contain much redundant and irrelevant feature, which will result in the curse of dimensionality. This situation will further lead to higher requirements and more challenges for the classification and recognition algorithm,need the feature selection algorithm to reduce the dimension of eigenvector and data noise.Aim at the dimension disaster introduced by the high dimension eigenvector,and the application oriented ATR algorithm,porpose an improved algorithm based on the sequential floating forward selection,by optimizing the repeat number of cross-test.The results of the simulation experiments shows that on the premise of the high classification accuracy,this improved algorithm can upgrade the calculation speed effectively and could maintain a more astringent and more stable confidence interval what means a better accuracy.
feature selection; SFFS; bayesian classifier; object recognition
2017-04-04;
2017-04-24。
周 阳(1984-),男,辽宁葫芦岛人,硕士研究生,主要从事信息集成与信息安全方向的研究。
1671-4598(2017)07-0294-04
10.16526/j.cnki.11-4762/tp.2017.07.073
TP751.1
A

