多模冗余可重构计算机可靠性研究

李兴伟，白 博，周 军

(西北工业大学，精确制导与控制研究所，西安 710072)

多模冗余可重构计算机可靠性研究

李兴伟，白 博，周 军

(西北工业大学，精确制导与控制研究所，西安 710072)

为了以最小代价提高多模可重构计算机的可靠性，需要结合系统体积功耗等因素,对不同计算机体系结构的可靠性进行评估；首先，针对三模冗余、三热一冷以及四模热备这几种不同冗余可重构计算机体系结构，给出了他们的故障状态转移图；其次，运用马尔可夫模型理论，对这些计算机结构进行可靠性建模；第三，根据上述3种系统的可靠性模型，在考虑失效率和维修率两个参数对系统可靠性影响的情况下，对各结构的可靠性指标进行了评价；结果表明，三热一冷的可靠性大于三模冗余，而小于四模热备；但综合考虑系统的可靠度、体积、功耗等因素后，在这几种形式的表决系统中，三热一冷是最优的；同时，设计完善的三模可重构系统可靠度会比一个设计不合理的四模可重构系统要高。

多模冗余；马尔可夫模型；可重构计算机

0 引言

近年来，随着大容量可重构FPGA的出现，扫除了可重构计算机技术在工程实现方面的障碍。与传统的计算机相比，可重构计算机在系统部分部件出现故障时，能够自主地改变自身的系统功能，使系统按原定性能指标或比原性能指标略有降低 (但可接受)的要求安全地完成任务。这样就避免了固定硬件结构的计算机一旦发生硬件损伤，将导致系统崩溃这一问题。

为了保证可重构计算机的可靠性指标，除了选择高质量的元器件外，普遍的做法是采用余度技术来实现这一目标[1]。常用的冗余结构有双机备份、二乘二取二、三模冗余、三热一冷等结构[2]。文献[3]阐述了两种不同工作策略的“二乘二取二”的可靠性与安全性，并与三模冗余系统进行了比较。文献[4]对双模冗余系统与三模冗余系统各系统的工作状态进行了详细分析，并利用马尔可夫过程对不同维修率和故障检测覆盖率对系统可靠度和安全度的影响进行了仿真计算。文献[5]对轨道交通里的三模冗余系统的可靠性与安全性进行了详细分析，并给出了故障检测率及维修率对三模冗余系统可靠性与安全性的影响。但以上文献并未对具有更多冗余器件的可重构系统的可靠性进行讨论。

本文针对由FPGA构成的几种比较典型的多模冗余可重构系统结构，利用马尔可夫过程对其进行可靠性建模。同时，在考虑系统失效率和维修率两个参数对系统可靠性影响的情况下，对各系统的可靠性指标进行了评价，分析了以最小代价提高多模可重构计算机可靠性的途径。

1 系统结构及工作原理

由FPGA构成的可重构计算机系统的最大特点是可以通过重新配置，进行系统的重构。这样当系统出现故障后，系统通过可重构机制使得系统得以修复。同时，为了进一步提高可重构计算机的可靠性，采用多模结构组成多模冗余可重构计算机系统。本文主要针对比较常用的三模冗余、三热一冷以及四模热备这几种冗余可重构计算机的可靠性进行分析。首先来看三模冗余系统。

1.1 三模冗余结构

图1所示为三模冗余系统结构图。

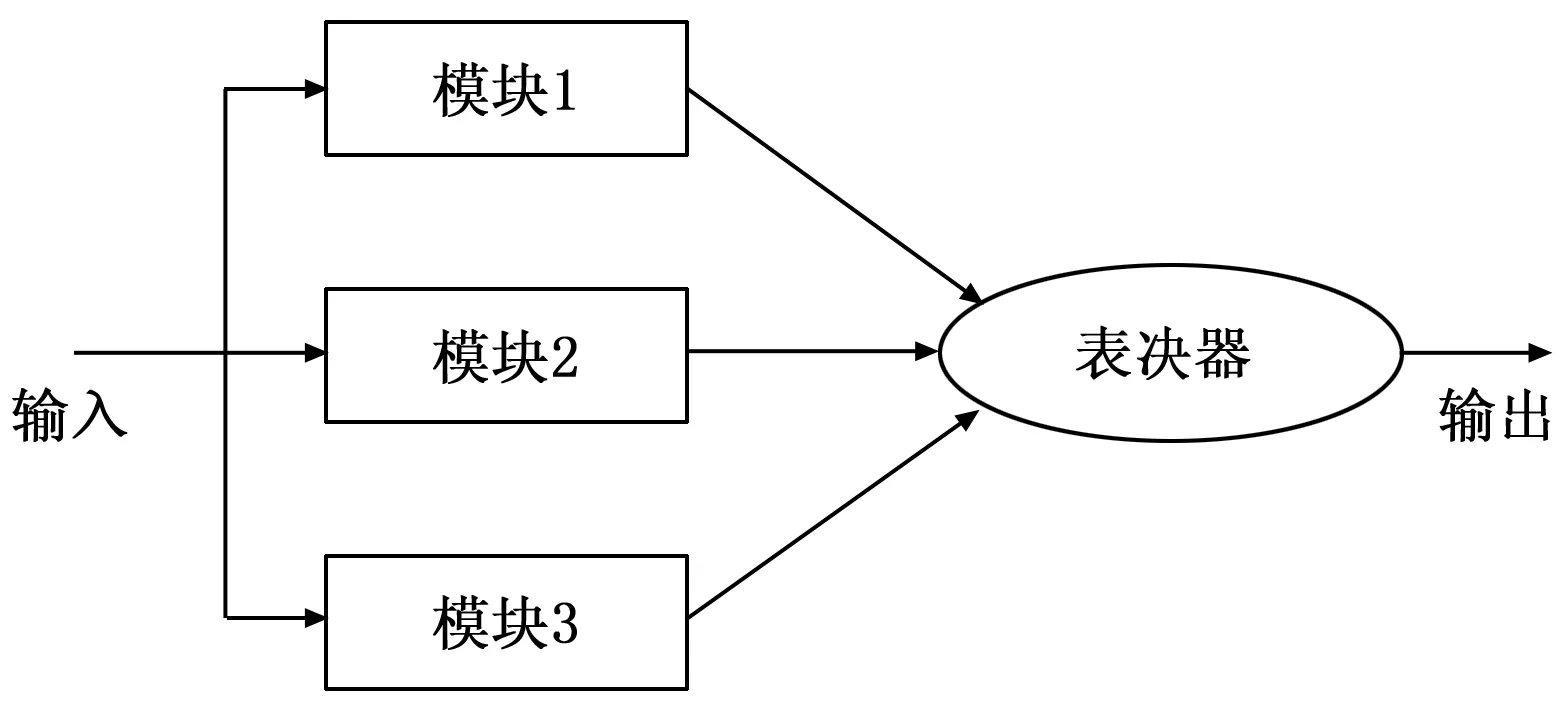
图1 三模冗余表决系统结构图

其工作原理是3个模块同时对输入信号进行运算处理，处理完毕后，送给表决器，由表决器选择输出。当3个模块的输出相同时，随机选择一个输出；当有两个模块输出相同而另一个模块输出不同时，从相同的两个模块中选择一个输出；当3个模块输出都不同时，系统产生报警。因此三模冗余可以屏蔽一个错误。

1.2 四模冗余结构

将图1所示的三模冗余表决系统再加上一模，这样就组成了四模冗余表决系统，如图2所示。

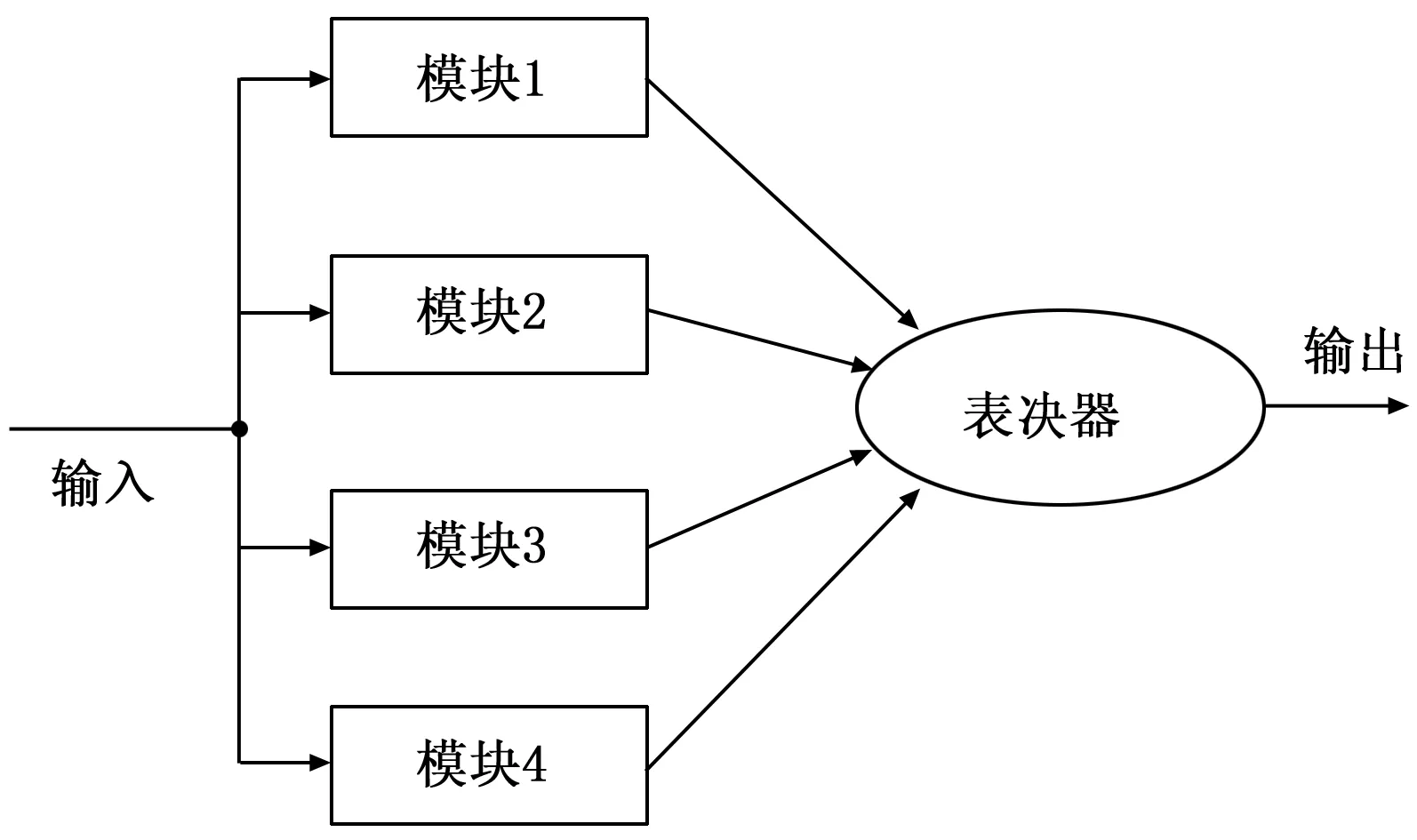
图2 四模冗余表决系统结构图

其工作原理是4个模块同时对输入信号进行运算处理，处理完毕后，送给表决器，由表决器选择输出。当4个模块的输出相同时，随机选择一个输出；当有两个模块输出相同而另两个模块输出不同时，从相同的两个模块中选择一个输出；当3个模块输出都不同时，系统产生报警。因此四模冗余可以屏蔽两个错误。

1.3 三热一冷冗余结构

将图1所示的三模冗余表决系统上再加一模冷备份，这样就组成三热一冷的冗余表决系统，如图3所示。

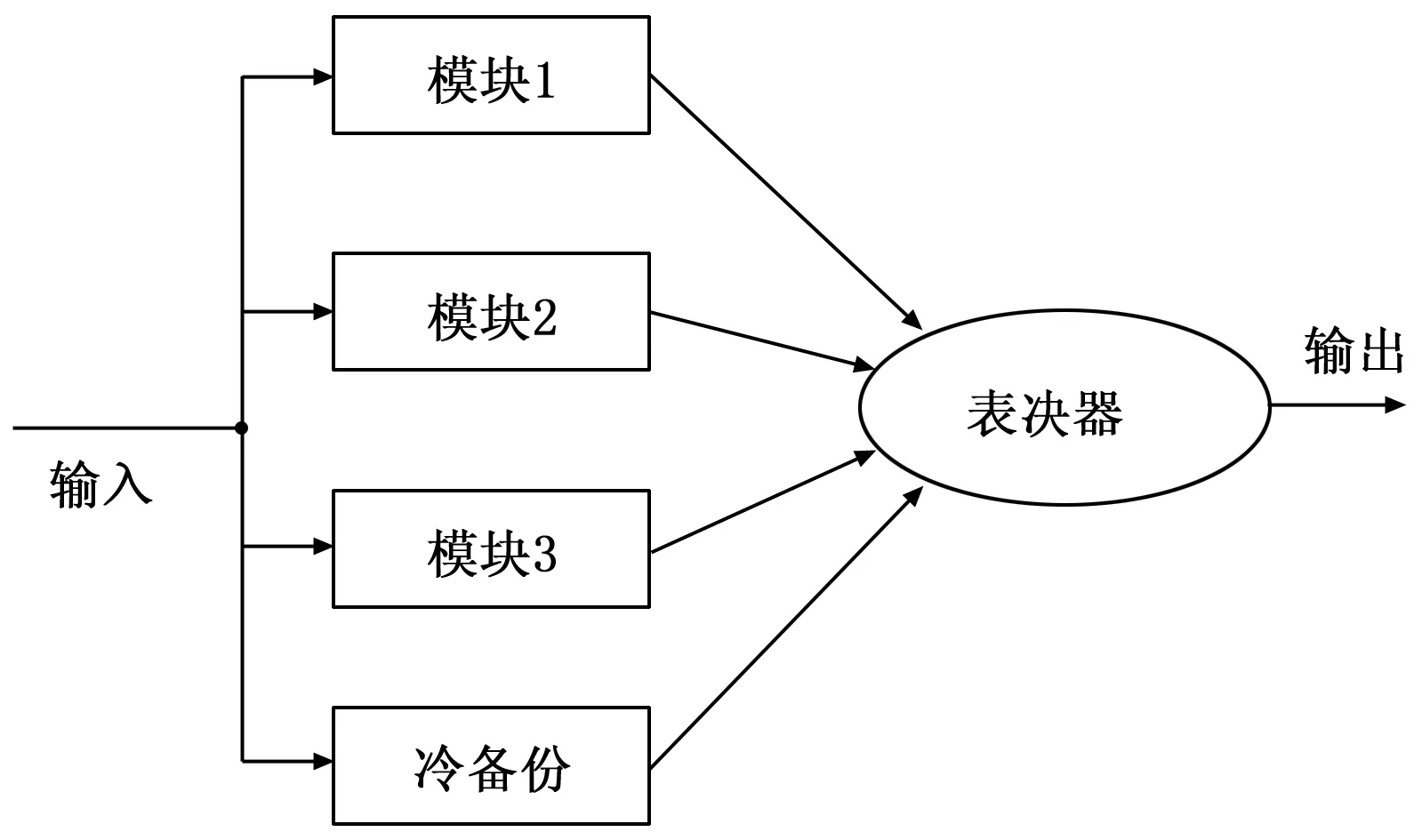
图3 三热一冷表决系统结构图

其工作原理如下，在正常情况下，由3个工作的模块同时对输入信号进行运算处理，冷备份模块不工作，表决器仅对3个工作模块的结果进行处理。当3个模块的输出相同时，随机选择一个输出；当有两个模块输出相同而另一个模块输出不同时，从相同的两个模块中选择一个输出；当有一个模块无法修复时，启动冷备份模块，重新构成三模冗余系统；当3个模块输出都不同时，系统产生报警。因此三热一冷冗余结构同样可以屏蔽两个错误，但其与四模冗余结构在可靠性上会有区别。

2 可靠性模型及分析

在研究各系统的可靠性之前，首先对系统做如下假设：

1)假设系统中除了几个计算机模块外，其他系统的可靠度均为1；

2)每个计算机模块的失效率为λ，系统维修率为μ，同时假设维修时间分布为指数分布；

3)某一时刻只有一个模块发生故障；

4)系统开始工作时，系统处于完好状态。

基于以上假设，对各结构的可靠性进行研究。

2.1 三模表决系统

对于图1所示的三模冗余表决系统，定义每个模块的维修率为常值μ，同时假设维修时间的分布为指数分布，则某一模块在时刻t处于失效状态，而在时刻t+Δt处于正常工作状态的概率为1-e-μΔt，将其按级数展开，对于很小的Δt，可简化为1-e-μΔt≈μΔt。

对于三模冗余表决系统，当且仅当至少有2个计算机正常时，系统才能工作。当有2个计算机故障时，系统故障，此时系统无法表决，系统停止输出。因此其马尔克夫状态可描述为：

1)定义随机变量X(t)=0，该状态表示时刻t时有0个计算机故障，此状态对应系统正常工作。称此状态为状态0。

2)定义随机变量X(t)=1，该状态表示时刻t时有1个计算机故障，在此状态下，系统仍能正常工作。称此状态为状态1。

3)定义随机变量X(t)=2，该状态表示时刻t时有2个计算机故障，在此状态下，系统故障。称此状态为状态2。

X(t)是一个齐次马尔可夫链。模块的失效率为常数λ，根据假设模块寿命的分布为指数分布，则某模块在时刻t处于正常状态，而在时刻t+Δt处于正常故障状态的概率为1-e-λΔt，将其按级数展开，对于很小的Δt，可简化为1-e-λΔt≈λΔt。由于系统由3个模块组成，因此系统从状态0到状态1的转移概率用语言来描述，则为3个模块中仅有1个模块出现故障。这样，由于有3个模块，该转移概率就为3λΔt。其它状态转移概率依此类推。系统的状态转移图如图4所示。

图4 三模冗余表决系统状态转移图

2.2 四模表决系统

如果将图1所示的三模冗余表决系统上再加一模，这样就组成四模冗余表决系统。同样定义模块的维修率为常值μ。根据假设维修时间的分布为指数分布，则某一模块在时刻t处于失效状态，而在时刻t+Δt处于正常工作状态的概率为1-e-μΔt，将其按级数展开，对于很小的Δt，可简化为1-e-μΔt≈μΔt。

对于四模冗余表决系统，当且仅当至少有2个计算机正常时，系统才能正常工作。当有3个计算机故障时，系统故障，此时系统无法表决，系统停止输出。其马尔克夫状态可描述为：

1)定义随机变量X(t)=0，该状态表示时刻t时有0个计算机故障，此状态对应系统正常工作。称此状态为状态0。

2)定义随机变量X(t)=1，该状态表示时刻t时有1个计算机故障，在此状态下，系统仍能正常工作。称此状态为状态1。

3)定义随机变量X(t)=2，该状态表示时刻t时有2个计算机故障，在此状态下，系统仍能正常工作。称此状态为状态2。

4)定义随机变量X(t)=3，该状态表示时刻t时有3个计算机故障，在此状态下，系统故障。称此状态为状态3。

X(t)是一个齐次马尔可夫链。模块的失效率为常数λ，根据假设模块寿命的分布为指数分布，则某模块在时刻t处于正常状态，而在时刻t+Δt处于正常故障状态的概率为1-e-λΔt，将其按级数展开，对于很小的Δt，可简化为1-e-λΔt≈λΔt。由于系统由4个模块组成，因此系统从状态0到状态1的转移概率用语言来描述，则为4个模块中仅有1个模块出现故障。这样，由于有4个模块，该转移概率就为4λΔt。其它状态转移概率依此类推。系统的状态转移图如图5所示。

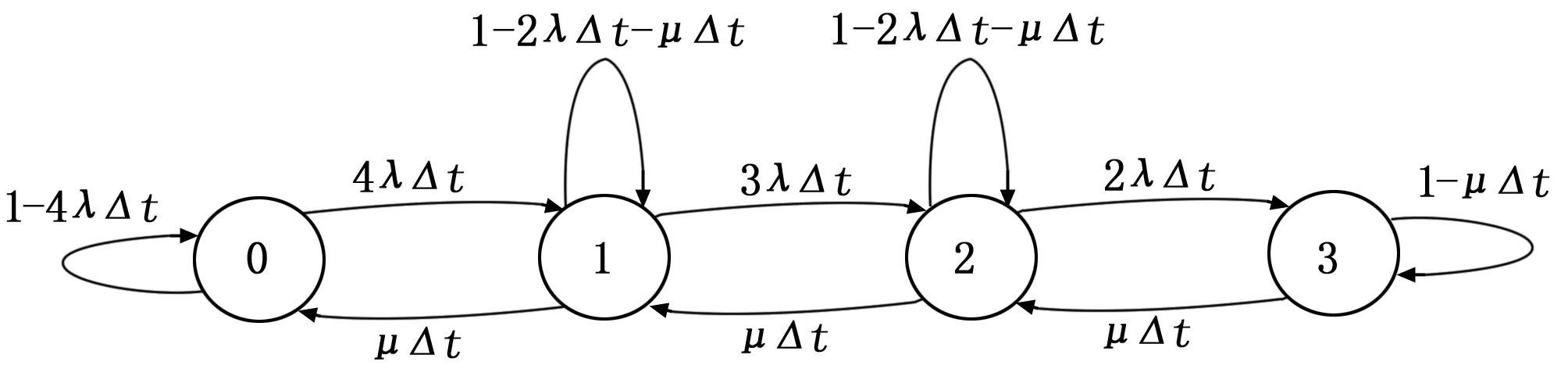
图5 四模冗余表决系统状态转移图

2.3 三热一冷表决系统

将图1所示的三模冗余表决系统上再加一模冷备份，这样就组成三热一冷的冗余表决系统。同样定义模块的维修率为常值μ。根据假设维修时间的分布为指数分布，则某一模块在时刻t处于失效状态，而在时刻t+Δt处于正常工作状态的概率为1-e-μΔt，将其按级数展开，对于很小的Δt，可简化为1-e-μΔt≈μΔt。

对于三热一冷的表决系统，仍然当且仅当至少有2个计算机正常时，系统才能正常工作。当有3个计算机故障时，系统故障，此时系统无法表决，系统停止输出。其马尔克夫状态可描述为：

1)定义随机变量X(t)=0，该状态表示时刻t时有0个计算机故障，此状态对应系统正常工作。称此状态为状态0。

2)定义随机变量X(t)=1，该状态表示时刻t时有1个计算机故障，在此状态下，系统将冷备份模块切换进来，系统组成仍为三模冗余，仍能正常工作。称此状态为状态1。

3)定义随机变量X(t)=2，该状态表示时刻t时有2个计算机故障，在此状态下，系统仍能正常工作。称此状态为状态2。

4)定义随机变量X(t)=3，该状态表示时刻t时有3个计算机故障，在此状态下，系统故障。称此状态为状态3。

X(t)是一个齐次马尔可夫链。模块的失效率为常数λ，根据假设模块寿命的分布为指数分布，则某模块在时刻t处于正常状态，而在时刻t+Δt处于正常故障状态的概率为1-e-λΔt，将其按级数展开，对于很小的Δt，可简化为1-e-λΔt≈λΔt。由于系统为三热一冷的形式，则在正常工作中，实际是三模系统在工作，因此系统从状态0到状态1的转移概率用语言来描述，则为3个模块中仅有1个模块出现故障。这样，由于仅计算3个模块，该转移概率就为3λΔt。而在状态1时，实际上系统仍为3模，因此状态1向状态2转移的概率仍为3λΔt。其它状态转移概率依此类推。系统的状态转移图如图6所示。

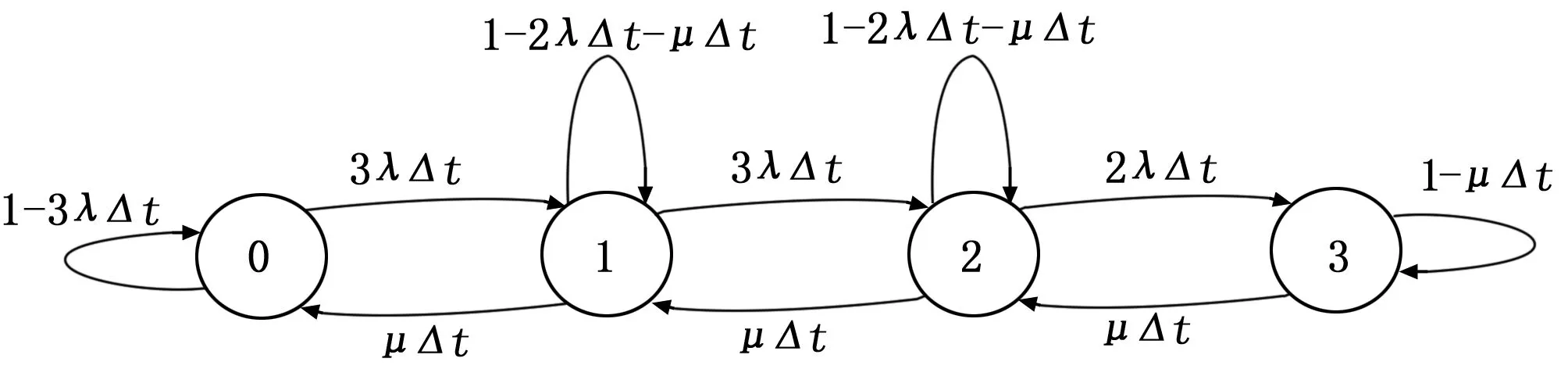
图6 三热一冷表决系统状态转移图

3 可靠性计算

根据以上的可靠性模型进行可靠性计算。

3.1 三模表决系统

根据图4所示的状态转移图，可得到如下转移概率，即条件概率。

P00=P{X(t+Δt)=0|X(t)=0}=1-3λΔt

(1)

P10=P{X(t+Δt)=1|X(t)=0}=3λΔt

(2)

P20=P{X(t+Δt)=2|X(t)=0}=0

(3)

P01=P{X(t+Δt)=0|X(t)=1}=μΔt

(4)

P11=P{X(t+Δt)=1|X(t)=1}=1-2λΔt-μΔt

(5)

P21=P{X(t+Δt)=2|X(t)=1}=2λΔt

(6)

P02=P{X(t+Δt)=0|X(t)=2}=0

(7)

P12=P{X(t+Δt)=1|X(t)=2}=μΔt

(8)

P22=P{X(t+Δt)=2|X(t)=2}=1-μΔt

(9)

现欲求X(t)在不同状态下的概率，P0(t)=P{X(t)=0}，P1(t)=P{X(t)=1}，P2(t)=P{X(t)=2}。根据全概率公式。

(10)

将式(1)～式(9)代入式(10)后，经过整理并求Δt→0的极限，可将式(10)写成微分方程组的形式。

(11)

考虑系统初始状态为正常的初值情况，[P0(t)P1(t)P2(t)]’=[1 0 0]’。利用拉普拉斯变换将微分方程变换成线性方程组后，解得[P0(s)P1(s)P2(s)]，再通过反拉式变换可解得时域解P0(t)，P1(t)，P2(t)。则据此可以算得三模表决系统的可靠度A3m(t)，

A3m(t)=P0(t)+P1(t)

(12)

3.2 四模表决系统

根据图5所示的状态转移图，可得到如下转移概率，即条件概率。

P00=P{X(t+Δt)=0|X(t)=0}=1-4λΔt

(13)

P10=P{X(t+Δt)=1|X(t)=0}=4λΔt

(14)

P20=P{X(t+Δt)=2|X(t)=0}=0

(15)

P30=P{X(t+Δt)=3|X(t)=0}=0

(16)

P01=P{X(t+Δt)=0|X(t)=1}=μΔt

(17)

P11=P{X(t+Δt)=1|X(t)=1}=1-(3λ+μ)Δt

(18)

P21=P{X(t+Δt)=2|X(t)=1}=3λΔt

(19)

P31=P{X(t+Δt)=3|X(t)=1}=0

(20)

P02=P{X(t+Δt)=0|X(t)=2}=0

(21)

P12=P{X(t+Δt)=1|X(t)=2}=μΔt

(22)

P22=P{X(t+Δt)=2|X(t)=2}=1-(2λ+μ)Δt

(23)

P32=P{X(t+Δt)=3|X(t)=2}=2λΔt

(24)

P03=P{X(t+Δt)=0|X(t)=3}=0

(25)

P13=P{X(t+Δt)=1|X(t)=3}=0

(26)

P23=P{X(t+Δt)=2|X(t)=3}=μΔt

(27)

P33=P{X(t+Δt)=3|X(t)=3}=1-μΔt

(28)

现欲求X(t)在不同状态下的概率，P0(t)=P{X(t)=0}，P1(t)=P{X(t)=1}，P2(t)=P{X(t)=2},P3(t)=P{X(t)=3}。根据全概率公式。

(29)

将式(13)～式(28)代入式(29)后，经过整理并求Δt→0的极限，可将式(29)写成微分方程组的形式。

(30)

考虑系统初始状态为正常的初值情况，[P0(t)P1(t)P2(t)P3(t)]’=[1 0 0 0]’。利用拉普拉斯变化将微分方程变换成线性方程组后，解得[P0(s)P1(s)P2(s)P3(s)]，再通过反拉式变化可解得时域解P0(t)，P1(t)，P2(t)，P3(t)。则据此可以算得四模表决系统的可靠度A4m(t)，

A4m(t)=P0(t)+P1(t)+P2(t)

(31)

3.3 三热一冷表决系统

根据图3所示的状态转移图，可得到如下转移概率，即条件概率。

P00=P{X(t+Δt)=0|X(t)=0}=1-3λΔt

(32)

P10=P{X(t+Δt)=1|X(t)=0}=3λΔt

(33)

P20=P{X(t+Δt)=2|X(t)=0}=0

(34)

P30=P{X(t+Δt)=3|X(t)=0}=0

(35)

P01=P{X(t+Δt)=0|X(t)=1}=μΔt

(36)

P11=P{X(t+Δt)=1|X(t)=1}=1-(3λ+μ)Δt

(37)

P21=P{X(t+Δt)=2|X(t)=1}=3λΔt

(38)

P31=P{X(t+Δt)=3|X(t)=1}=0

(39)

P02=P{X(t+Δt)=0|X(t)=2}=0

(40)

P12=P{X(t+Δt)=1|X(t)=2}=μΔt

(41)

P22=P{X(t+Δt)=2|X(t)=2}=1-(2λ+μ)Δt

(42)

P32=P{X(t+Δt)=3|X(t)=2}=2λΔt

(43)

P03=P{X(t+Δt)=0|X(t)=3}=0

(44)

P13=P{X(t+Δt)=1|X(t)=3}=0

(45)

P23=P{X(t+Δt)=2|X(t)=3}=μΔt

(46)

P33=P{X(t+Δt)=3|X(t)=3}=1-μΔt

(47)

现在欲求X(t)在不同状态下的概率，P0(t)=P{X(t)=0}，P1(t)=P{X(t)=1}，P2(t)=P{X(t)=2},P3(t)=P{X(t)=3}。根据全概率公式。

(48)

将式(32)～式(47)代入式(48)后，经过整理并求Δt→0的极限，可将式(48)写成微分方程组的形式。

(49)

考虑系统初始状态为正常的初值情况，[P0(t)P1(t)P2(t)P3(t)]’=[1 0 0 0]’。利用拉普拉斯变化将微分方程变换成线性方程组后，解得[P0(s)P1(s)P2(s)P3(s)]，再通过反拉式变化可解得时域解P0(t)，P1(t)，P2(t)，P3(t)。则据此可以算得三热一冷表决系统的可靠度A3h1c(t)，

A3h1c(t)=P0(t)+P1(t)+P2(t)

(50)

4 可靠性验证及分析

根据式(12)、式(31)、式(50)可以分析与比较失效率和修复率对不同形式系统可靠性的影响。根据目前国内器件的平均失效率分析，取单台计算机的失效率λ=0.001/h。图7显示了失效率λ=0.001/h，模块的维修率μ=0.1/h的情况下，不同系统形式的可靠度随时间变化的曲线。

由图中我们可以看出，3种形式的可靠度最后都趋向于常值，这是由于本文仅研究系统稳定可靠期所致。实际上，随着时间的推移，最终产品都会趋向于失效，这已超出本文所研究的范围。由图中可以看出，在相同失效率和修复率的情况下，三热一冷的可靠度最高，约为99.99825%，四模热备份的可靠度约为99.99770%，三模热备份的可靠度最低，约为99.94178%。

虽然四模热备的可靠度和三热一冷的可靠度很相似，但在

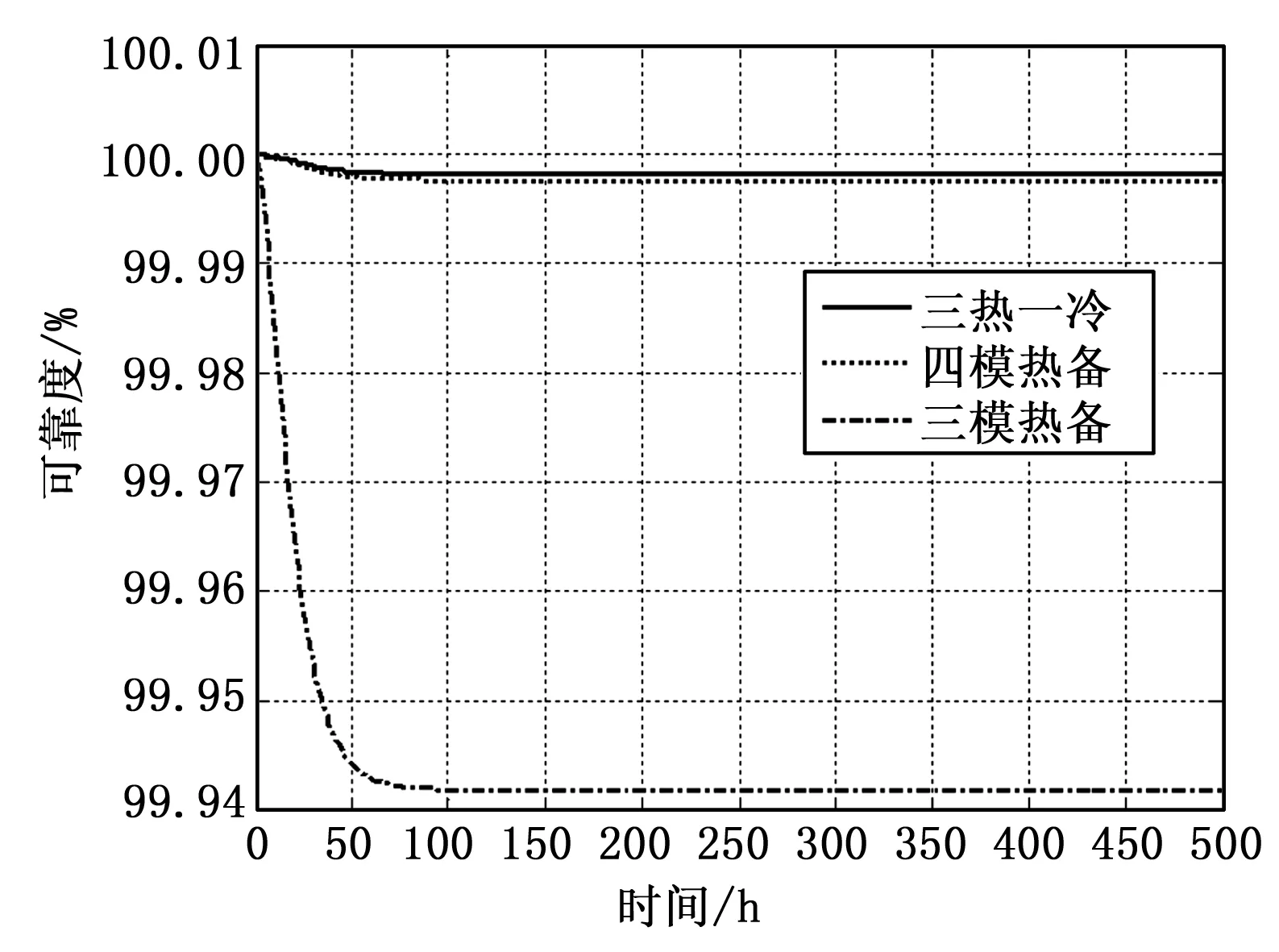
图7 不同形式表决系统的可靠度比较

实际使用过程中，三热一冷的系统形式始终有一模处于冷的状态，这样对于减小系统功耗是有利的。因此，在四模热备、三热一冷、三模热备这几种形式的表决系统中，三热一冷是最优的。

而对于可重构系统，其修复率不仅取决于硬件结构的设计，同时也取决于可重构系统软件的架构。下表显示了不同修复率情况下，不同系统形式的可靠度变化。

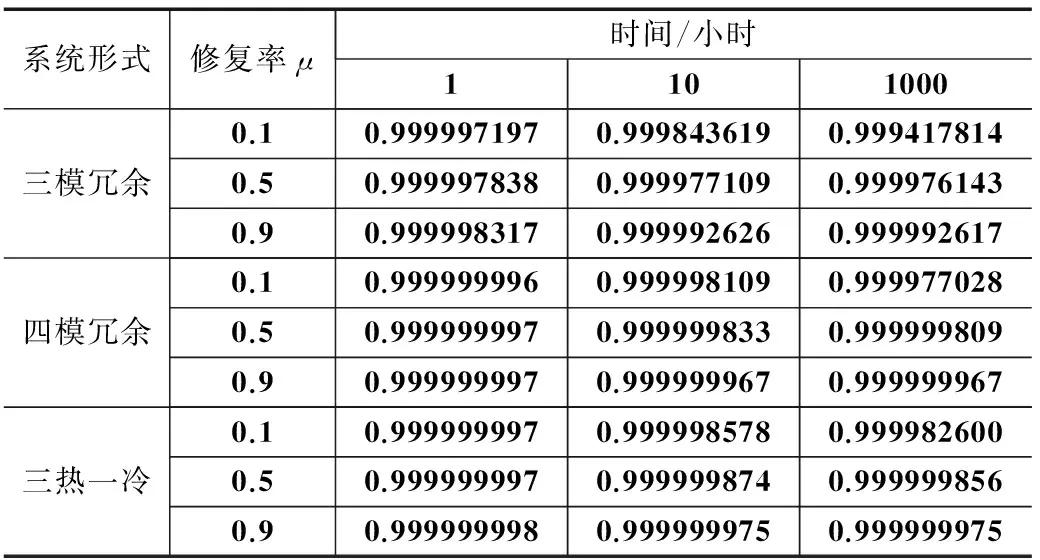
表1 修复率以及系统构成对系统可靠度的影响

由该表可以看出，如果提升修复率后，各系统形式的可靠度均有上升。在高修复率的情况下，三模系统的可靠度能达到低修复率的四模系统。这一点说明，对于三模系统，如果重构系统设计完善，对不同故障都能够修复，那么该三模系统的可靠度会比一个设计不合理的四模系统要高。

通过以上分析可以得到如下两点结论：

1)综合考虑系统的可靠度、体积、功耗等因素后，在四模热备、三热一冷、三模热备这几种形式的表决系统中，三热一冷是最优的。

2)对于三模可重构系统，需要设计完善的重构机制，尽量修复不同的故障模式，那么该三模系统的可靠度会比一个设计不合理的四模可重构系统要高。

5 结论

本文针对比较常用的三模冗余、三热一冷以及四模热备这几种冗余可重构计算机的可靠性进行分析。在一定的假设条件下，对比了这几种体系结构的可靠性。结果表明，在综合考虑系统的可靠度、体积、功耗等因素后，在四模热备、三热一冷、三模热备这几种形式的表决系统中，三热一冷是最优的。同时，如果三模可重构系统的重构机制设计完善，修复率较高，那么该三模系统的可靠度会比一个设计不合理的四模可重构系统要高。因此在这几种多模冗余可重构计算机体系结构中，可优先考虑三模冗余结构。如果对可靠性有进一步的要求，可选择三热一冷的结构形式。

[1] Majid Asadi，Ismihan Bayramoglu.The Mean Residual Life Function of a k-out-of-n Structure at the System Level [J].IEEE Transactions on Reliability，2006，55(2)：314-317.

[2] 李荣强，姜巍巍，曹德舜.基于典型冗余结构的安全仪表系统可靠性对比分析 [J].安全技术，2015，15(8)：11-13.

[3] 张本宏，陆 阳，韩江洪，等.“二乘二取二”冗余系统的可靠性和安全性分析[J].系统仿真学报，2009，21(1)：256-261.

[4] 武晓春，高雪娟.双模冗余-比较系统与三模冗余系统的性能比较[J].自动化与仪器仪表，2012，164(6)：169-171.

[5] 陈 州，倪 明.三模冗余系统的可靠性与安全性分析[J].计算机工程，2012，38(14)：239-245.

Study on Reliability of Multiple Modular Redundant Reconfigurable Computer

Li Xingwei, Bai Bo, Zhou Jun

(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072, China)

In order to improve the reliability of multiple modular reconfigurable computers with minimum cost, the reliability of different computer architectures need to be evaluated with system power and volume consideration. First, considering the redundant reconfigurable computer architecture of triple modular redundancy (TMR), quadruple modular redundant (QMR)and triple modular with one cold backup, the fault state transition diagrams of these architectures are proposed. Second, the reliability models of these computer systems are built with Markov model. Third, considering the influences of reliability with failure rate and maintenance ratio, the reliability of different structure are evaluated based on the above three models. The comparison of three results indicates that, the reliability of triple modular with one cold is less than the reliability of QMR, while it is bigger than the reliability of TMR. But after considering the factors of reliability, system volume and power consumption, the triple modular with one cold is optimal. And the reliability of a perfectly designed TMR reconfigurable system will be higher than that of a bad designed QMR reconfigurable system.

multiple modular redundant; Markov model; reconfigurable computer

2016-12-27；

2017-02-06。

航天支撑技术基金(2015-HT-XGD);西北工业大学基础研究基金(JC201205)。

李兴伟(1974-)，男，内蒙古人，博士研究生，主要从事飞行器导航、制导与控制方面的研究。

1671-4598(2017)07-0309-04

10.16526/j.cnki.11-4762/tp.2017.07.077

TP302.8

A