非概率可靠性在浮空器中的应用*
刘国梁,朱增青
(中国电子科技集团公司第三十八研究所, 安徽 合肥 230088)
非概率可靠性在浮空器中的应用*
刘国梁,朱增青
(中国电子科技集团公司第三十八研究所, 安徽 合肥 230088)
浮空器属航空产品,其设计的可靠性直接影响产品的安全性。目前,浮空器产品大多是非批量生产,缺乏大样本数据,可靠性评估可利用区间非概率可靠性理论进行描述。文中论述了非概率可靠性基本理论,通过建立浮空器产品囊体结构失稳数学模型推导了囊体结构区间非概率可靠性指标的计算公式,然后以典型囊体结构件为算例,结合实验给出了囊体结构非概率可靠性指标数据曲线,对比了数值模拟和实验测算结果,得出理论值相对实测值偏保守的结论。非概率可靠性方法可反映结构在不同载荷状态下的可靠程度,对工程应用具有一定的指导作用。
非概率可靠性;浮空器;囊体
引 言
浮空器是指密度轻于空气的飞行器,是系留气球和飞艇的统称[1-2]。随着新技术的出现以及材料科学的发展,浮空器迎来了快速发展的阶段。到目前为止,研制生产浮空器的国家至少有十几个,在经济生活和军事斗争中应用的浮空器型号和数量更多,如美国在伊拉克部署的快速升空浮空器平台(REAP) 、在阿富汗部署的快速初始部署浮空器(RAID) 以及正在研发的平流层飞艇计划等。国内对浮空器产品做了广泛研究,文献[3]和[4]对浮空器外形和结构做了论述,并对充气薄膜结构强度进行了实验验证。
浮空器属于复杂且贵重的航空产品,非批量生产,故极其缺乏与可靠性相关的统计数据,属于小样本和贫信息的情况。传统的可靠性评估一般采用概率的方法,但当产品的真实统计数据难以获得或计算模型不够精确时,概率可靠性评估方法就难以获得高的置信度。文献[5]于20 世纪90 年代中期提出了非概率的可靠性概念,文献[6]对其做了进一步的研究和完善。非概率可靠性的优点是对原始数据要求很低,只需知道不确定参量的界限,不要求其具体的分布形式,且不涉及概率的概念,不必求其概率密度函数或隶属函数。非概率可靠性提出后,很多人都予以了关注,先后提出了区间可靠性、稳健可靠性等方法,并开展了多方面的应用研究。
本文针对浮空器产品小样本特性,将区间可靠性理论引入浮空器可靠性判定中,得出软体结构浮空器产品的区间可靠性指标,通过实验对理论区间可靠性指标与实际结构失稳状态下的非概率可靠性指标进行了对比。
1 区间变量的表示与区间非概率可靠性
若不确定性参量V在区间[VL,VU]内变化,则V∈VI=[VL,VU]为区间变量,其中,VL为V的区间下界,VU为V的区间上界,VI为V的实值区间。令:
VC=(VU+VL)/2;VR=(VU-VL)/2
(1)
则有:
VL=VC-VR;VU=VC+VR
(2)
且VI和V可分别表示为:
VI=[VL,VU]=VC+VRΔI
V=VC+VRΔ
(3)
式中:VC、VR分别为区间[VL,VU]的均值和离差;ΔI=[-1,1]为标准化区间;Δ∈ΔI为标准化区间变量。
显然,VI可由VC、VR两个参数唯一确定。对区间非概率可靠性的度量描述如下:设2个相互干涉的区间变量对应的功能函数:
MI=RI-SI
(4)
式中,RI和SI分别表示强度和应力区间变量,根据式(3)处理得:
RI=Rc+RrΔI;SI=Sc+SrΔI
(5)
式中:Rc和Sc分别为强度和应力区间变量的均值;Rr和Sr分别为强度和应力区间变量的离差。
将式(5)代入式(4),整理得:
MI=(Rc-Sc)+(Rr-Sr)ΔI
(6)
定义非概率可靠性指标:
(7)
当结构的不确定参数为区间变量时,可以认为结构只是2种确定性状态:可靠或不可靠。无量纲量η=1为可靠的临界值,当η>1时系统可靠,且η值越大,结构的安全程度越高。因而可以将η作为结构安全可靠程度的度量。
2 充气模型临界弯曲载荷[4,7]
封闭膜结构在充气状态下,薄膜中存在预应力,在弯曲载荷作用下产生挠曲时,其截面管壁的一侧受到附加的轴向拉应力,另一侧受到附加的轴向压应力。当弯曲载荷达到一定值时,压应力大于管内部气压产生的轴向拉应力,受压一侧的管壁开始产生褶皱,如图1所示。进一步弯曲,褶皱将从受压一侧沿截面管壁的周向不断扩展,直到布满整个截面[7]。
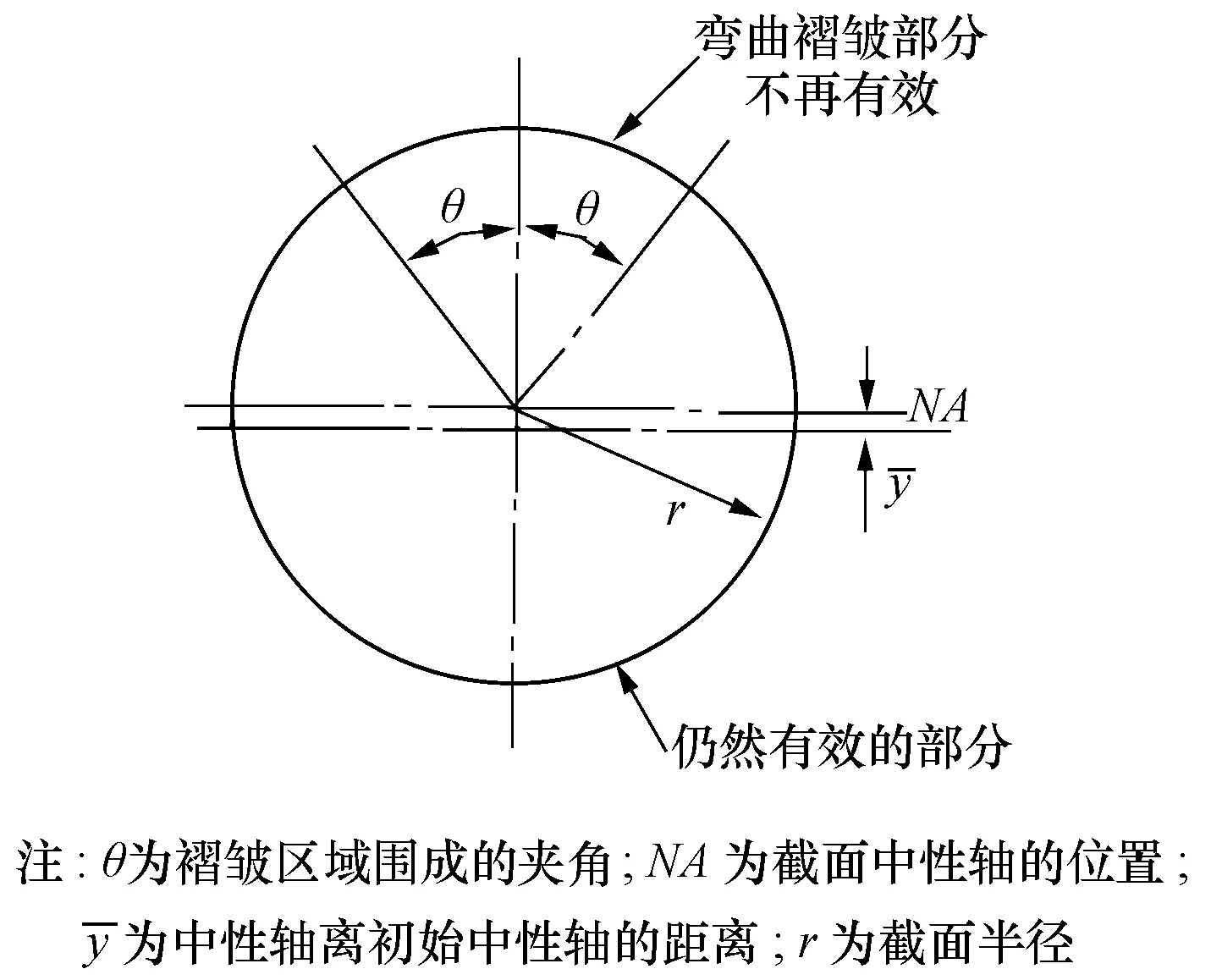
图1 充气模型横截面的褶皱区
充气状态的弹性薄膜充气管,薄膜中的轴向预张力T(单位为N/m,公式不包含薄膜厚度)为:
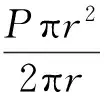
(8)
式中:P为充气管内外压差;r为充气管截面半径。
在横向力作用下发生挠曲时,截面上弯矩产生的轴向张力T′为[3]:
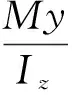
(9)
图2为弯矩产生的轴向应力图。当y= ±r时,截面上的轴向张力有最大值。在固定端的底部,弯矩产生的轴向压应力最大,会最先出现褶皱。该点的轴向张力T″为:
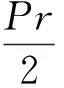
(10)
当T″=0时结构失稳,由此得到的载荷定义为临界载荷,用Fcr表示,计算公式如下:
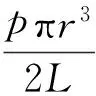
(11)
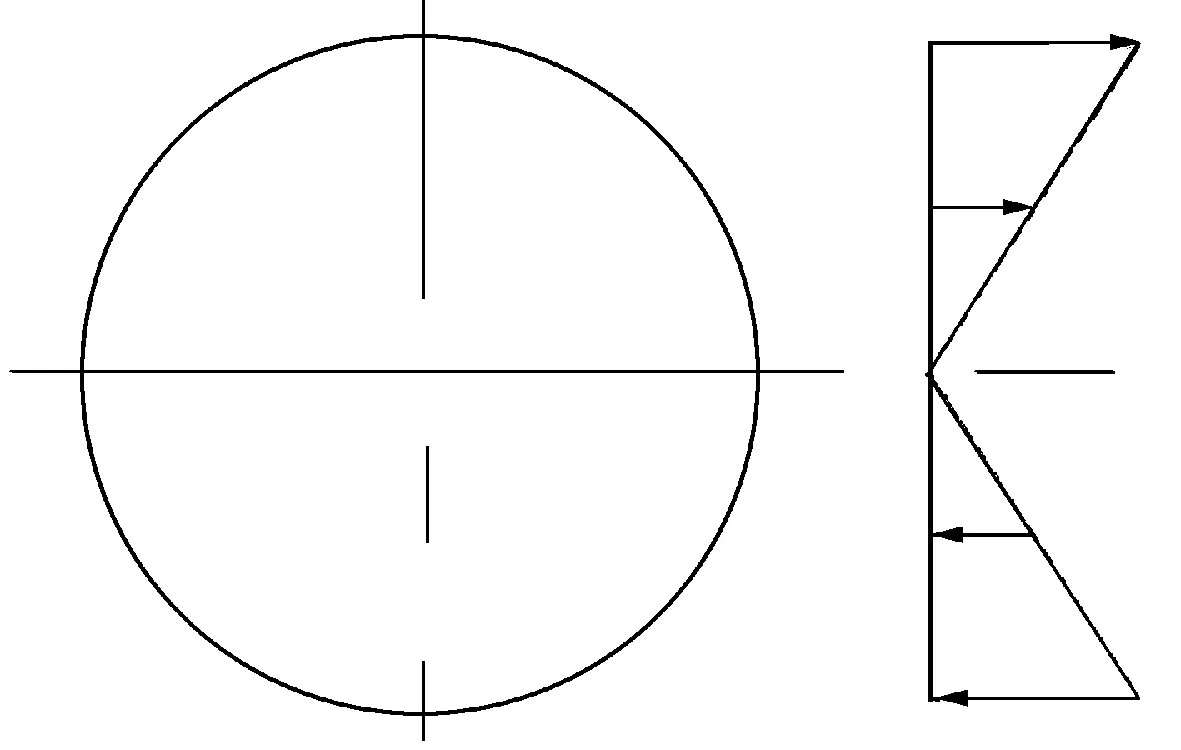
图2 弯矩产生的轴向应力
当载荷超过临界载荷时,囊体出现褶皱的区域不再有效,惯性矩及中心轴也发生了改变,不再是线性变化的过程。
3 充气模型非概率可靠性模型
浮空器囊体生产确定以后,可以认为其为确定性结构。由于囊体材料本身有一定的透气率,囊体发生变形也会引起内压的变化,囊体充气后,内压P存在一定的变化量。因缺少大样本统计数据,故无法确定压力变化符合某一种概率统计模型。所以将内压P定义为区间变量,P在区间[PL,PU]范围内变化。根据式(11)得:
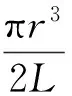
(12)
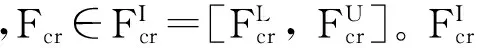
充气能够使封闭膜结构获得原薄膜材料所不具备的抗弯强度和刚度,增加充气压力能够提高承载能力。在工程中,不但要求充气囊体结构有足够的强度、刚度,还要求有很好的稳定性。囊体结构弯曲失效是一个渐进的过程,当所受载荷小于临界载荷值时,膜结构惯性矩及中心轴可近似为线性变化;当载荷超过临界载荷时,囊体出现褶皱区域不再有效,惯性矩及中心轴也发生了改变,不再是线性变化的过程。当囊体出现褶皱,充气囊体变形将出现突变,可以认为此时囊体结构已不可靠,不能满足结构稳定性要求。根据首次穿越失效理论,建立区间非概率干涉模型:
(13)
式中:FI为区间弯曲载荷,FI=[FL, FU]。FL为区间下界,FU为区间上界。
则囊体结构区间非概率可靠性指标:
(14)
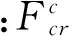
4 充气模型试验
4.1 试验装置
试验装置如图3所示,模型总长100 cm,直径为16 cm,加载点在距离固定端80 cm位置,测量点在距离固定端60 cm处,两者不在一个位置的原因主要是考虑到加载点的局部变形会影响到测量精度[4]。

图3 试验模型图
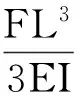
(15)
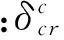
4.2 试验步骤
试验选择内压为10kPa,将模型充到规定压力,端部载荷采用砝码的形式进行施加,从零载荷开始,直至模型失去承载能力,试验重复3次。
本次实验提供了3个结构相同的试验件,重复相同的实验步骤,得出3组实验数据,最后对实验数据进行分析,符合小样本量、小数据的概念。
4.3 试验结果
充气模型失稳状态如图4所示,模型根部产生了大量的褶皱,模型变形急剧增加,最终失去了承载能力。

图4 模型失稳图
将内压为10kPa工况下的试验载荷与测量的变形绘制成如图5所示的曲线。试验数据曲线的前半部分近似为线性,在模型发生褶皱后,模型的位移也加速变大,在最后阶段,位移急剧增加,模型失去承载能力,模型最终试验失稳载荷为19.4N。
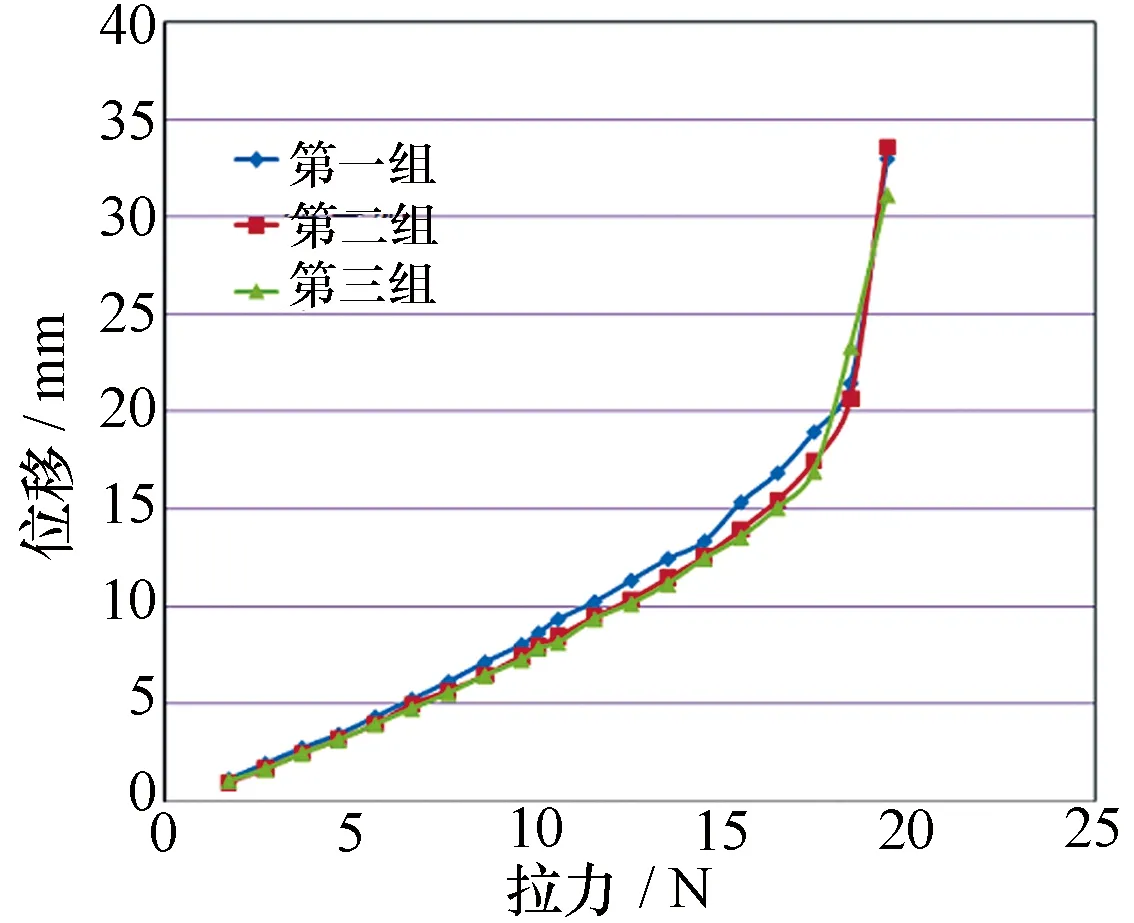
图5 模型的载荷位移曲线
整理实验所得数据,转化为区间数,绘制区间数变化曲线,如图6所示。分别以理论临界载荷10.05N,试验失稳载荷19.4N为阀值,绘制非概率可靠性指标曲线,如图7所示。
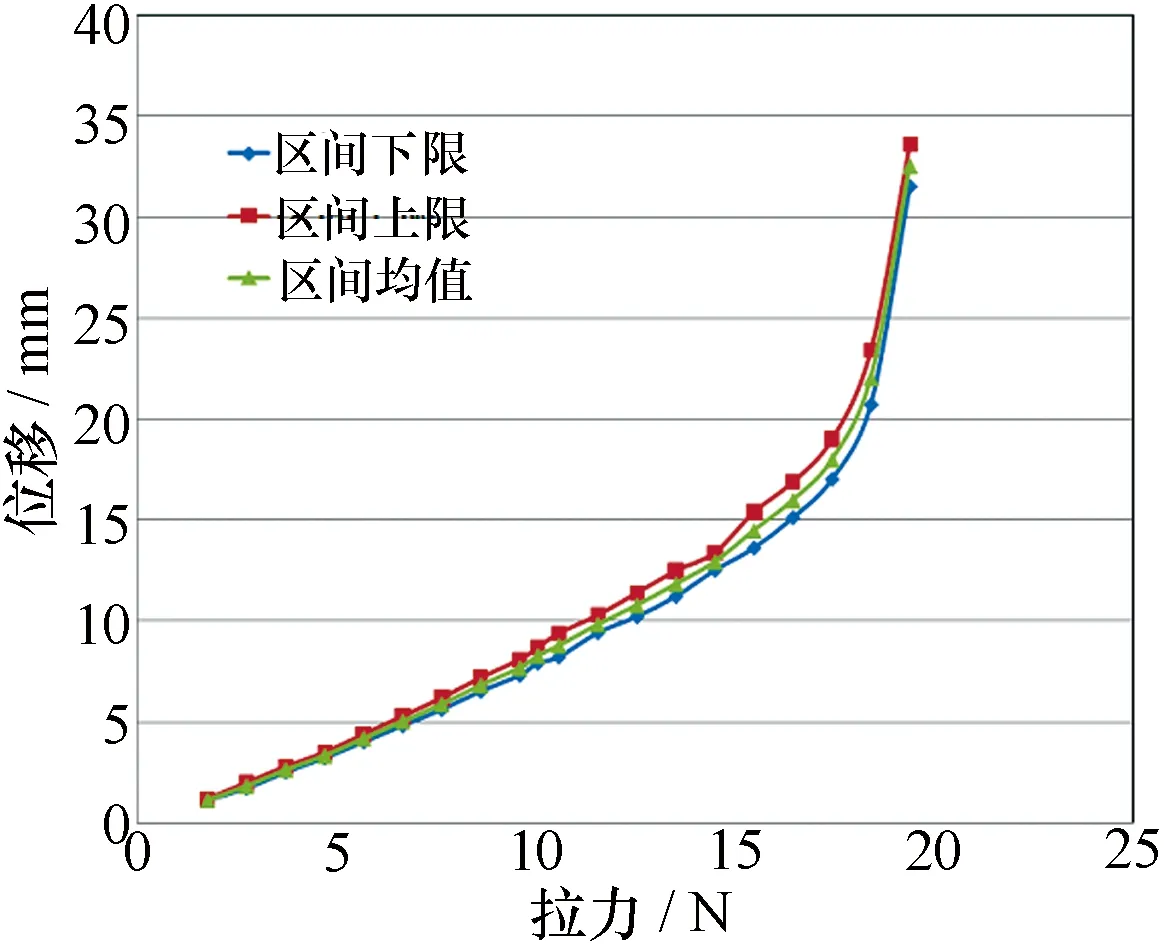
图6 模型的载荷位移区间曲线
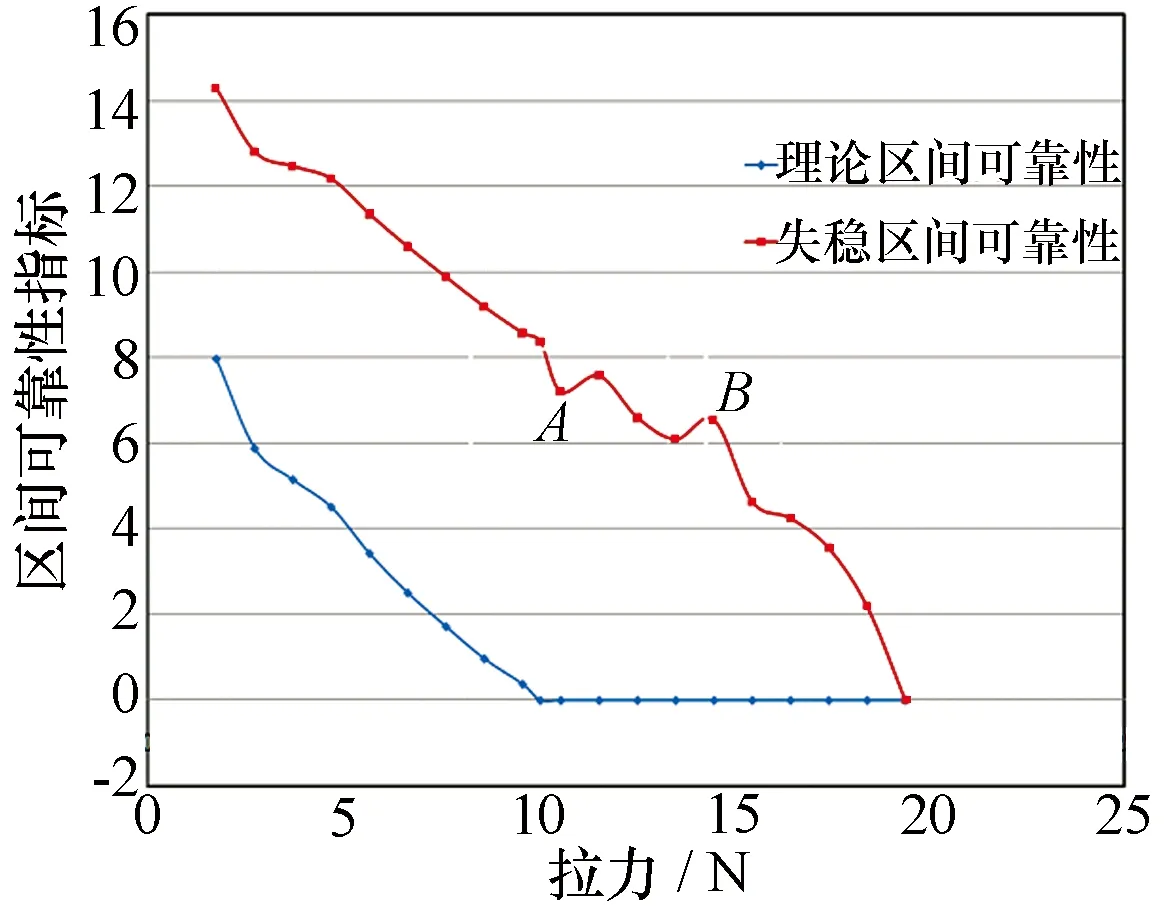
图7 模型区间可靠性曲线
5 结果分析
在10kPa的充气压力工况下,试验模型的理论临界失稳载荷的理论计算值为10.05N,试验中的失稳载荷为19.4N,试验失稳载荷为理论临界载荷的1.93倍,说明在模型出现褶皱后仍然具有较强的承载能力。
将实验数据转换为区间数,创建区间模型,计算得到区间非概率。如图6所示,实验初期和实验失稳前区间变化较小,随后区间变化逐渐变大,表明在低载荷下结构变化较小,实验数据相对集中;结构越接近失稳状态,测试结果变化越大,实验数据分布越发散。如图7所示,理论临界载荷之前的区间可靠性指标下降趋势平稳,近似为线性变化。当外载荷超过理论临界载荷值时,理论区间可靠性指标为零;失稳区间可靠性指标变化加剧,图中曲线斜率逐渐变大,失效加速。图中有2处突变点,发生突变的原因为:1)该实验只进行3次,实验样本较少,区间覆盖率小;2)A点相对相邻两点处区间离差变大,B点相对相邻两点处区间离差变小,引起两处区间概率可靠性指标发生突变。总体趋势是下降的,符合工程实际情况。
6 结束语
本文进行了充气模型的临界载荷及试验分析,并对实验数据进行了区间参数处理,得出了结构的非概率区间可靠性数据曲线。在理论临界失稳载荷之前,充气模型变形与载荷之间可近似为线性关系。超过理论临界载荷之后,模型产生褶皱,褶皱区域随着载荷的增加而扩大,最终失去承载能力。区间非概率可靠性模型很好地反映了这种变化趋势。根据不同的强度指标绘制相应的非概率可靠性曲线,反映结构在不同载荷状态下的可靠程度,对工程应用具有一定的指导作用。
[1]HEMBREEB,SLEGERSN.Tetheredaerostatmodelingusinganefficientrecursiverigid-bodydynamicsapproach[J].JournalofAircraft, 2015, 48(2): 623-632.
[2] 张平, 王平安. 某浮空器抓手结构力学性能仿真与试验[J]. 电子机械工程, 2016, 32(5): 30-33.
[3] 成琴, 袁军行, 唐逊, 等. 系留气球囊体外形优化研究[J]. 西安航空技术高等专科学校学报, 2012, 30(3): 42-45, 70.
[4] 王平安. 薄膜充气梁失稳载荷研究[J]. 西安航空技术高等专科学校学报, 2014, 32(3): 7-10.
[5]BENHAIMY.Convexmodelsofuncertaintyinradialpulsebucklingofshells[J].JournalofAppliedMechanics, 1993, 60(3): 683-688.
[6]QIUZP,ELISHAKOFFI.Anti-optimizationofstructureswithlargeuncertainbutnon-randomparametersviaintervalanalysis[J].ComputerMethodsinAppliedMechanicsandEngineering, 1998, 152(3): 361-372.
[7] 库利GA, 吉勒特JD. 飞艇技术[M]. 王生, 译. 北京: 科学出版社, 2007: 133-134.
刘国梁(1979-),男,博士,工程师,主要从事浮空器总体设计工作。
Application of Non-probabilistic Reliability to Aerostat
LIU Guo-liang,ZHU Zeng-qing
(The38thResearchInstituteofCETC,Hefei230088,China)
As aviation product, the design reliability of aerostat affects its security. Usually the aerostat is not produced in batch, so it lacks large sample data. The reliability evaluation of the aerostat can be described by interval non-probabilistic reliability theory. In this paper the basic non-probabilistic reliability theory is firstly expounded. Then, the instability mathematical mode for envelope structure of the aerostat is established and the formula of interval non-probabilistic reliability index is deduced. Finally, with an example of the typical envelope structure piece, the reckoning method of non-probabilistic reliability index of envelope structure is obtained based on the experiment. By contrasting the numerical simulation result and experiment reckoning result, it is found that the theory result is more conservative. Non-probabilistic reliability method can reflect the structural reliability level under different loads, which can be used as guidance for engineering application.
non-probabilistic reliability; aerostat; envelope
2017-02-21
国家863计划资助项目(2015AA8098085E)
V215.9
A
1008-5300(2017)02-0018-04

