某型机载雷达天线伺服系统的动力学分析*
汤伟强,陈腾飞
(南京电子技术研究所, 江苏 南京 210039)
某型机载雷达天线伺服系统的动力学分析*
汤伟强,陈腾飞
(南京电子技术研究所, 江苏 南京 210039)
对某型机载雷达的天线伺服系统进行了动力学分析。首先根据天线结构和伺服单元结构的特点建立了有限元模型,然后在Patran/Nastran中进行了动力学分析,包括模态分析、冲击响应分析、频率响应分析、随机振动分析等,全面评估此系统的动力学特性。此分析计算为后续的结构设计优化、动力学设计提供了重要依据。
机载雷达;天线座;动力学分析;有限元
引 言
随着电子技术的发展,越来越多的电子设备装载到航空飞行器上,因而飞行器对于各类电子设备的减重要求越来越高[1-3],但是环境力学条件是保持不变的或者要求更高。这样在设计过程中,电子设备的刚强度富裕程度就越来越小,因此在设计过程中需要对电子设备进行全面的动力学特性评估和校核,保证结构的安全性和可靠性。对于机载雷达这一重要的航空电子设备,动力学特性分析尤为重要,特别是整个系统的动力学特性分析更能充分地反映整体结构动力学设计的优劣[4]。
本文对某型机载雷达的天线伺服系统进行了全面的动力学分析。首先把Pro/E模型导入到Hypermesh中进行结构简化和网格划分,然后设定边界条件。把有限元模型导入到Patran中根据不同的分析类型设定不同工况,提交到Nastran中进行分析计算。最后根据分析结果评估系统的动力学性能。
1 有限元模型的建立
1.1 伺服单元有限元模型建立
动力学分析求解应力时对网格质量要求比较高,因此为获得较高可行度的结果,对伺服单元进行六面体结构化网格划分。将结构中的电路板、传感器等简化为质量点通过MPC(多点约束)连接到安装位置的节点上。在传动轴上轴承的内圈外圈之间建立有6向刚度的PBUSH单元以模拟轴承,见图1。部件与部件之间如果螺钉孔较多就用共节点的方式进行连接,如果螺钉孔较少,则用MPC连接。
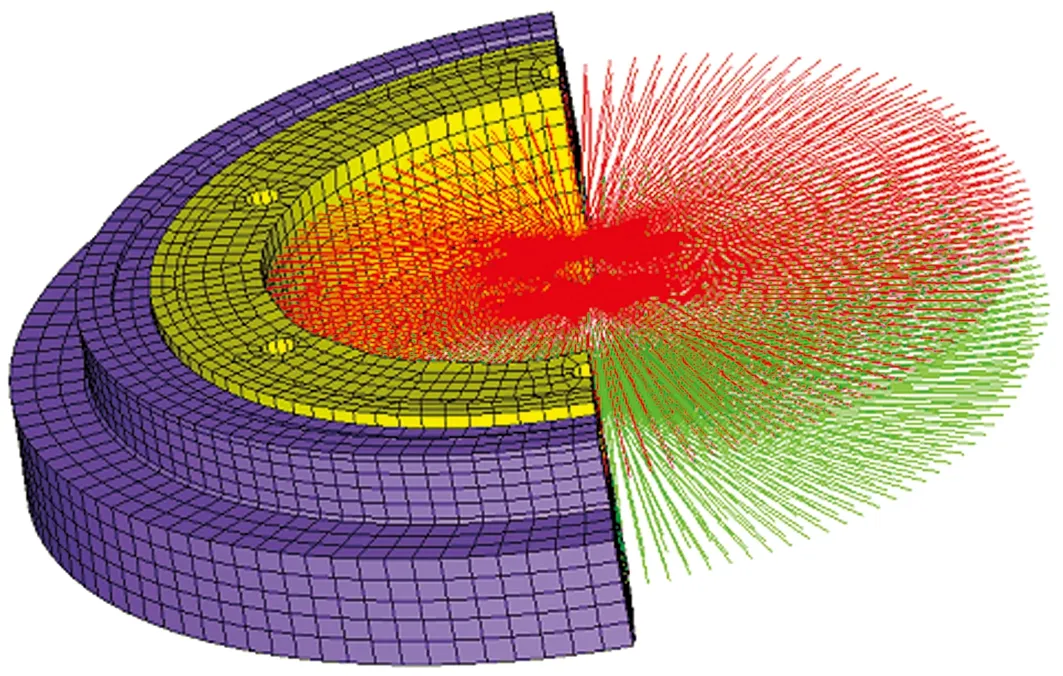
图1 轴承PBUSH单元
1.2 天线单元有限元模型建立
由于天线结构大多数属于薄板壳类结构,因此将天线的大部分结构划分为壳单元网格,其余结构划分为六面体网格,风扇简化为质量点。模块的销钉连接采用4个自由度的MPC来模拟。天线与天线座支臂之间的6个螺钉连接采用MPC约束螺母大小区域网格节点来模拟。整个模型的单元数为566 484个,节点数达到725 274个。整个系统的有限元模型如图2所示。
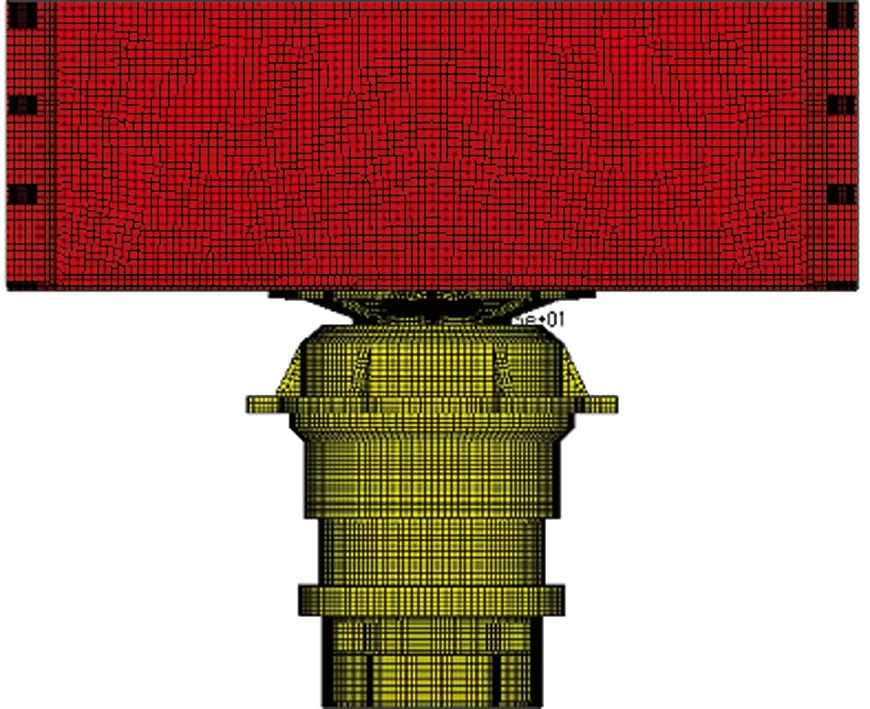
图2 整体有限元模型
2 环境条件
冲击响应分析是计算结构在瞬间力作用下的响应。冲击载荷按照GJB 150.18A[5]的方法,采用后峰锯齿波。在随机响应工况中3个轴向采用相同的功率谱,功率谱密度的量值见GJB 150.16A[6]。
3 动力学分析
3.1 模态分析
采用Block Lanczos的方法进行模态求解,结果如表1所示。
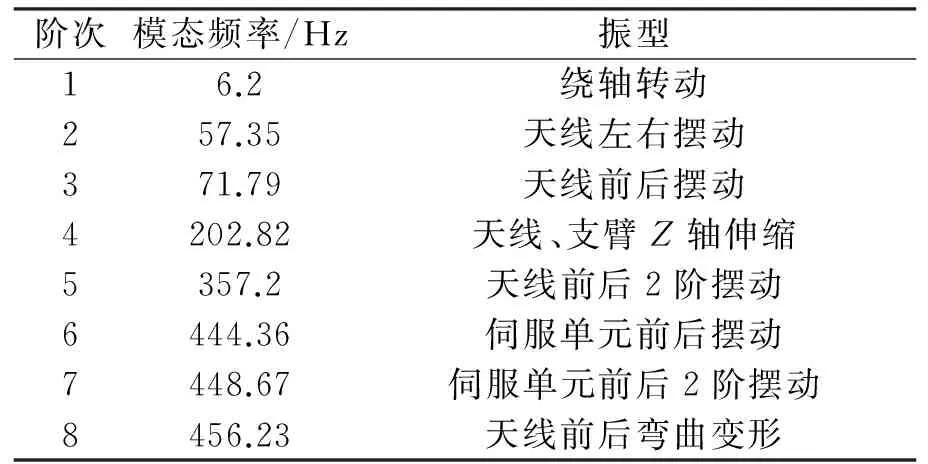
表1 系统前8阶固有频率和振型
第1阶为轴承引起的自由模态,第2、3阶的振型如图3所示。
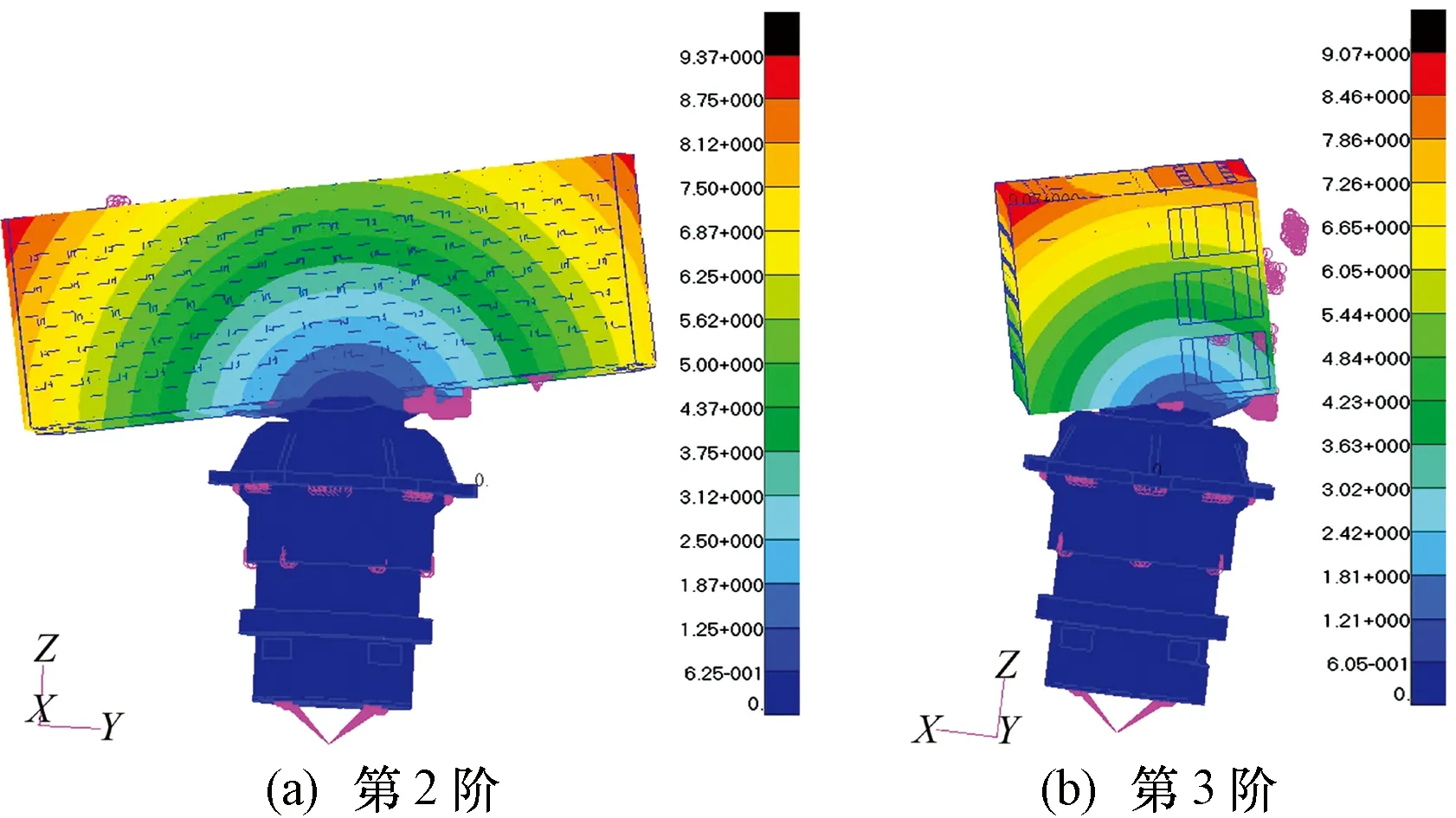
图3 第2、3阶振型
第1阶模态频率较高,天线伺服系统整体刚度较好。第3阶模态振型所对应的模态刚度比第2阶小,与实际相符。
3.2 冲击响应分析
采用模态法计算天线伺服系统的冲击响应。响应最大值出现在向前冲击工况的天线支臂位置,结果如图4所示。从图中可以看出,支臂向前冲击工况下应力响应最大值为230 MPa,除去应力集中区,其他区域最大应力值在153~200 MPa之间。支臂材料为2A14,屈服强度为360 MPa。因此在模型向前冲击工况下,这个零件是安全的。

图4 支臂应力云图
3.3 频率响应分析
在天线座支臂固定螺纹孔区域节点处分别施加3个方向的单位正弦加速度载荷,分析得到结构各处的加速度响应曲线。选择天线单元安装点(左右对称)一边的3个节点(945020、943923、933320)提取频响曲线,见图5。其中向上加载工况的加速度放大倍数较大。
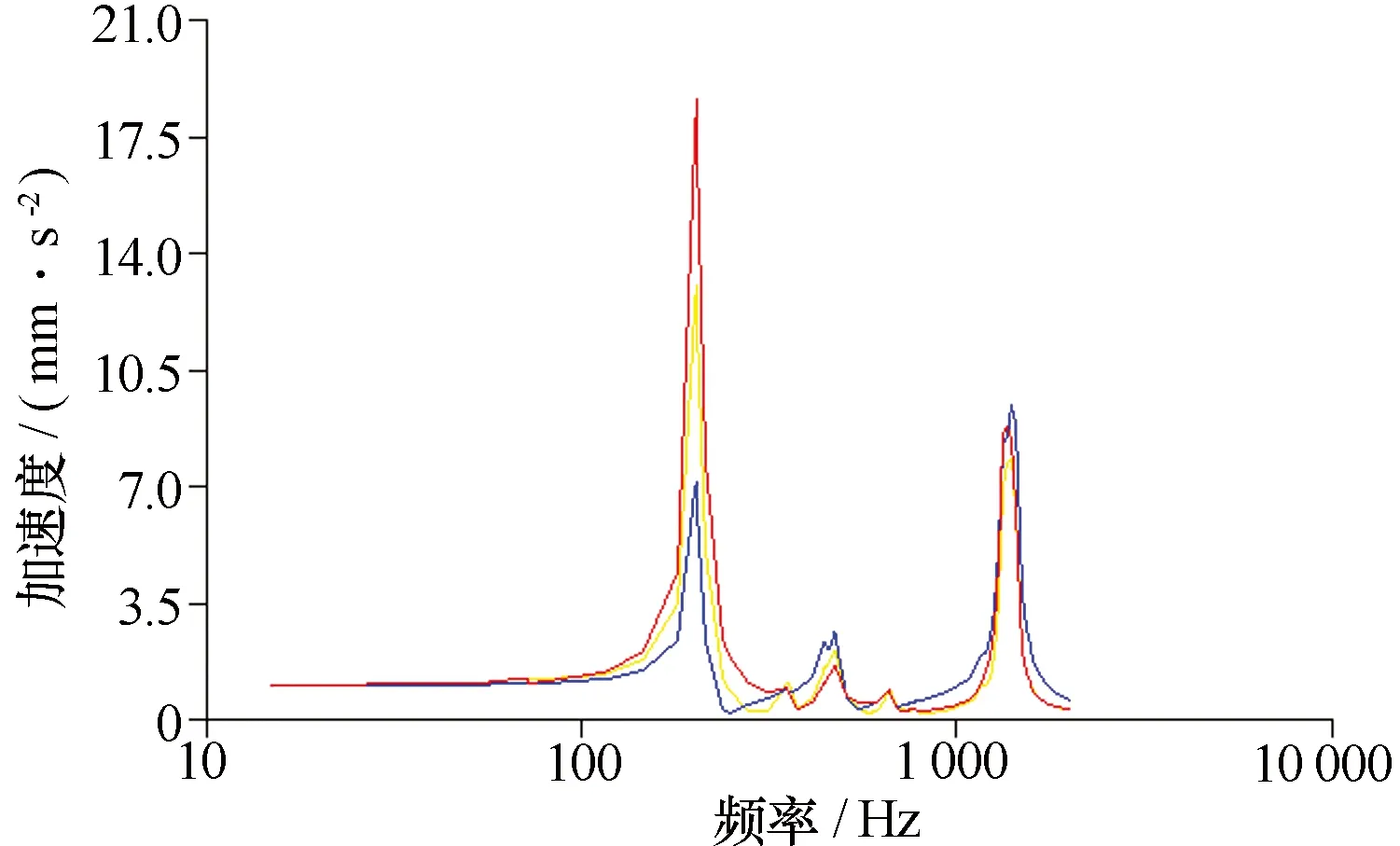
图5 加速度频响曲线
由图5可见, 202.82 Hz的加速度频率响应值最大,为节点933320的18.6 mm/s2,放大了18.6倍,放大倍数在可接受范围内。模型受到模态分析中第4阶的影响最大。
3.4 随机振动分析
MSC Nastran对随机振动的分析是作为频率响应的后处理进行的。在3个工况的功率谱密度加载后,结果显示应力最大值出现在向前加载工况的天线座支臂上,支臂的随机振动响应应力云图如图6所示。从图中可以看出,支臂随机振动响应应力最大,最大值为58.3 MPa。云图中的应力值为1σ应力,因此3σ应力的最大值应为174.9 MPa。支臂的屈服强度为360 MPa,结构安全系数为2.05,满足要求。
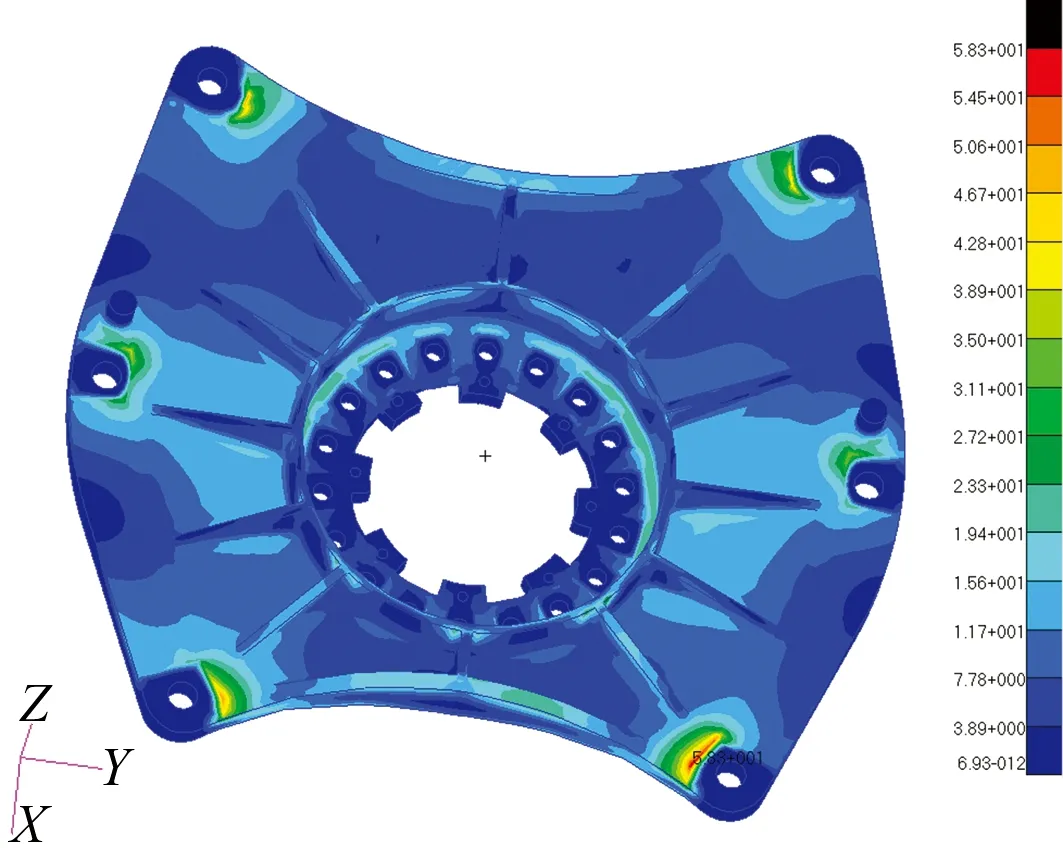
图6 支臂随机振动响应应力云图
测节点17876(伺服单元外壳固定孔处)、222295(伺服单元底部壳)、943964(支臂孔处)的功率谱密度响应,节点17876的RMS值为5.853g,这表示输入载荷的RMS值为5.853g。节点943964的RMS值为10.94g,放大1.87倍。节点222295的RMS值为19.12g,放大3.27倍。具体的功率谱密度响应曲线如图7所示。

图7 功率谱密度响应曲线
整个模型的RMS分布云图如图8所示,最大值为29.6g,是输入功率谱密度RMS值的5倍。可见伺服单元和天线的RMS值放大倍数都在合理范围内。
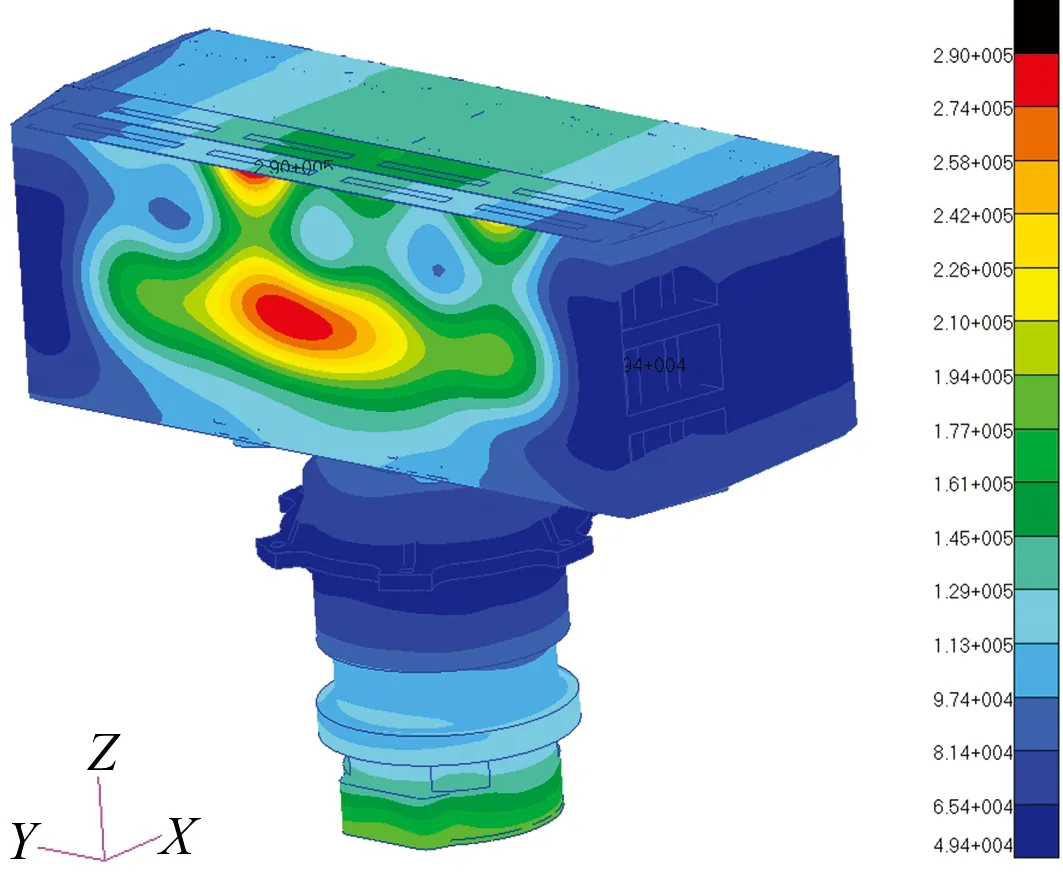
图8 RMS分布云图
4 试验验证
通过3向扫频试验获得结构前4阶固有频率,与仿真模型对比结果如表2所示。

表2 结构固有频率对比
由误差可见仿真结果有效,要进一步提高仿真精度,需要对仿真模型进行修正。
天线伺服系统的整体刚度对前4阶的模态频率值贡献较大,而天线座支臂是两部分连接的枢纽,因此支臂的连接刚度对整体刚度影响较大。原有限元模型采用RBE2单元多节点约束支臂孔和天线对应孔的周围节点。现提出用梁单元模拟螺钉连接,梁单元两端分别采用MPC约束相应孔周围节点。此方法能够更精确地模拟螺钉连接。
由于天线结构复杂,难以精确建模,在建模过程中进行了简化。原有限元模型只是保证了天线的重心、质量和实际模型相近。现提出更改模型,使转动惯量和实际模型相近,提高模型精度。
5 结束语
通过对天线伺服系统进行模态分析、冲击响应分析、频率响应分析、随机振动分析,得到动力学分析结果,评估系统的各项动力学性能指标均满足要求。通过和试验数据对比,前4阶模态频率误差在3.1%内,说明仿真模型有效。针对仿真模型提出2条模型修正建议,在后续工作中实施。仿真结果对后续的结构动力学设计、优化设计有借鉴意义。
[1] 梁震涛, 徐德好, 李玉峰, 等. 直升机载设备安装架的随机振动分析[J]. 电子机械工程, 2009, 25(5): 21-24.
[2] 王贤宙, 王长武. 基于MD.Nastran的某型机载雷达机箱力学仿真分析[J]. 电子机械工程, 2011, 27(1): 12-14.
[3] 任翠锋, 牛忠文, 苏涛, 等. 基于某无人机平台的测云雷达结构动力学分析[J]. 测绘通报, 2014(S1): 94-98.
[4] 洪长满, 段勇军. 机载雷达天线座结构的刚强度性能评估[J]. 现代雷达, 2011, 33(6): 72-75.
[5] 李传日. GJB 150.18A—2009 军用装备实验室环境试验方法 第18部分:冲击试验[S]. 北京: 国防科学技术工业委员会军用标准化中心研究室, 2009.
[6] 施荣明. GJB 150.16A—2009 军用装备实验室环境试验方法 第16部分:振动试验[S]. 北京: 国防科学技术工业委员会军用标准化中心研究室, 2009.
汤伟强(1965-),男,工程师,主要从事科技管理工作。
Dynamic Analysis of Antenna Servo System of an Airborne Radar
TANG Wei-qiang,CHEN Teng-fei
(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
Dynamic analysis of the antenna servo system of an airborne radar is carried out in this article. First of all, the finite element model is constructed according to the structure characteristics of antenna and servo unit. Then dynamic analysis such as modal analysis, transient response analysis, frequency response analysis, random vibration analysis are performed using Patran/Nastran in order to evaluate the dynamic property of the system comprehensively. Analysis result of the article provides critical reference for future structure design optimization and dynamic design.
airborne radar; antenna pedestal; dynamic analysis; finite element
2016-12-27
TN820.3
A
1008-5300(2017)02-0031-03

