弧门三叉斜支臂扭角的验算与求证

卢俊生，秦红兵

（中国水利水电第十一工程局有限公司，河南 郑州450001）

1 引言

三叉斜支臂是近年来新出现的结构类型。当孔口尺寸较大时，弧形闸门高度随之增高，原有的上、下两支臂结构不能满足承载力与稳定性要求，采用三根支臂组成的斜支臂用于超大型弧形闸门应运而生。为便于区别，将三根支臂组成的斜支臂简称三叉斜支臂。三根支臂分别与门叶上布置的三个主横梁连接，所以又称作三主梁斜支臂弧门。

因为需要承受整个门叶的水压力，支臂（截面形状常为工字梁、或箱形梁）的腹板，最佳的受力状态是位于弧面与支铰轴线形成的径向平面上，与主梁腹板保持在同一个平面。因此，需要有意识地绕中线扭转一个角度，这就是所谓斜支臂的扭角。扭角不正确会恶化斜支臂的受力状态，可能造成斜支臂失稳甚至扭转弯折诱发事故。

对于由上、下两根支臂组成的斜支臂（以下简称V型斜支臂），“斜支臂水平偏斜角α，上、下支臂夹角2θ，与扭转角φ三个角度之间的函数关系”，在《水利水电工程钢闸门设计规范》SL74-2013，以及《水电工程钢闸门设计规范》NB35055-2015（P23，6.1.11条款）已经明确规定其计算公式：

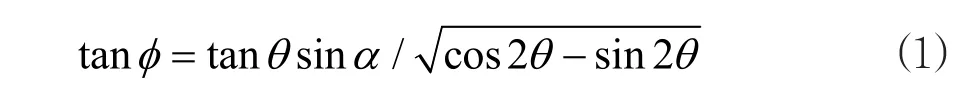
通过研究发现：上述规定只适用于V型斜支臂结构类型。因为三叉斜支臂结构类型比较少见，现行《设计规范》相应的技术条款尚未涵盖此结构类型。

2 总体思路

依据数学的基本原理与定理作为理论基础，对弧形闸门三叉斜支臂的空间几何形状进行分析，推导求证出支臂结构中：水平偏斜角；上、中支臂中线的夹角（包括中、下支臂中线的夹角）；在支铰的垂直端面上形成的扭角等相关角度之间存在的函数关系，并总结出详细的计算公式。

验证方法是：弧形闸门三叉斜支臂扭角的数学计算与三维数学模型相结合。采用Autodesk inventor软件建立三叉斜支臂的三维模型，通过模型在立体空间自然形成的角度加以验证，校验计算公式的正确性。

3 数学公式的推导与求证

3.1 建立三叉斜支臂计算模型

根据三叉斜支臂结构特点，简化成数学计算模型，设定计算条件及符号代表的内容。如图1为弧形闸门三叉斜支臂左侧支臂的结构简图：L1、L2分别表示上中、中下支臂对应的弧门面板弧长。BACO所在平面为过上、中、下主梁与斜支臂前端板中心交点的垂直剖面，该垂面与侧墙面、弧门纵向中心面平行。直线BO、AO、CO分别是上、中、下支臂中线在垂面的投影，O点为支铰轴线在垂面的中心点。当支臂处于BACO平面时，因为与主梁垂直即为直支臂，BO与AO的夹角θ1′，CO与AO的夹角θ2′分别代表上中、中下支臂之间的夹角。可以作如此的假设：当支铰中心O点沿支铰轴线向左侧平移一个距离（即为支臂的水平偏斜距离）到达O1点，分别连接B、A、C与O1点得到BO1、AO1、CO1直线。形成三个直角△BO1O、△AO1O、△CO1O，因为共一个直角短边且长边相等，所以，BO1与BO的夹角、AO1与AO的夹角、CO1与CO的夹角均相等，该角即是斜支臂的水平偏斜角α；BO1、AO1、CO1构成的面即为三叉斜支臂的中心面。在此情况下，BO1与AO1的夹角θ1，CO1与AO1的夹角θ2分别代表斜支臂上中、中下支臂之间的夹角。

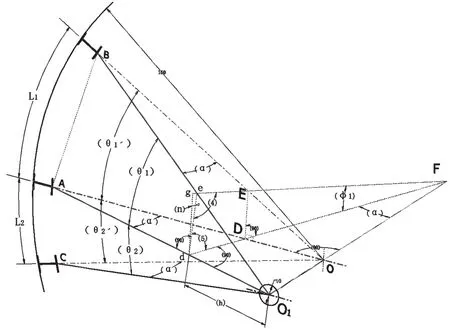
图1 弧形闸门三叉斜支臂左侧支臂线框简图

3.2 斜支臂与直支臂夹角换算关系

设定式中：L1、L2-对应面板的弧长；θ1、θ2-斜支臂上中、中下支臂之间的夹角；R-弧门面板圆弧半径；

θ1′、θ2′- 斜支臂上中、中下支臂在侧墙平面投影的夹角，即直支臂上中、中下支臂的夹角。

弧长与角度的计算公式：

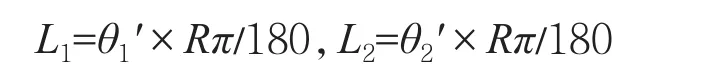
斜支臂与直支臂夹角换算公式：

此半角公式可以化为整角公式：

3.3 斜支臂扭角求证

为方便求证，将中支臂所在的平面AOO1置于水平面，在AO合适位置上作该平面的垂线ED，与AO、BO交于D、E点，ED⊥AO，且ED⊥AOO1平面。

过D点作AO1的垂线交于d点，且另一端与OO1的延长线交于F点，dF⊥AO1。再以两条直线ED和dDF建立一个平面edDFE，该平面与中支臂中心线垂直即为斜支臂后端板与铰链连接的垂直端面，到中心点O1的距离h即为铰链的高度。eEF与dDF直线形成的夹角φ1即为上支臂腹板平面相对中支臂腹板平面的扭角。

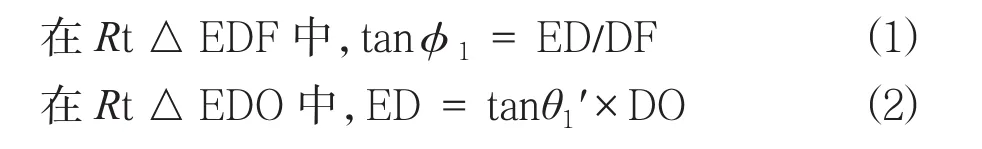
因为AO⊥OO1（即O1F），所以△AO1O为直角三角形。又因为dF⊥AO1，所以△O1dF、△DOF同为直角三角形，Rt△AO1O与Rt△O1dF共一个余角，所以∠DFO＝α。

这即是上支臂腹板中线的扭角公式。

同理可以得出下支臂腹板的扭角公式：

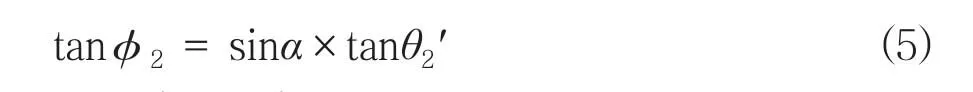
对比《规范》的“6.1.11”公式，可以得出结论：现行规范给出的弧门斜支臂扭角计算公式，只适合于V型斜支臂弧门，不能涵盖采用三叉斜支臂结构的弧形闸门。

3.4 支臂后端板平面上、下支臂与中支臂中心连线夹角的求证

三叉斜支臂上、中、下支臂的三条中线并不在同一个平面内。因此，在后端板平面上三个交点的连线同样不在一条直线上。

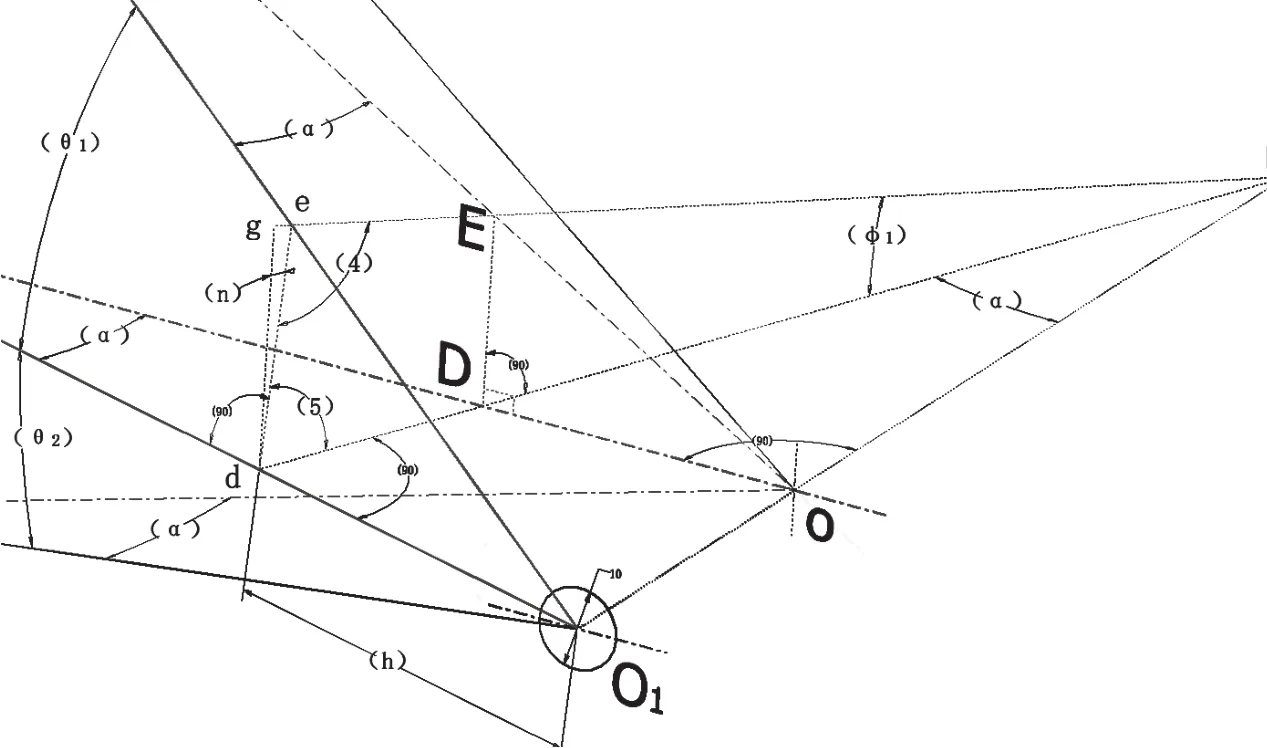
图2 三叉斜支臂弧门左侧支臂线框简图后端板处放大图

图2是图1的局部放大图。平面dDFOO1是三叉斜支臂中支臂构成的平面，将其置于水平位置，其中dO1是中支臂中线的一部分。平面edDFE垂直于水平面dDFOO1且与dO1垂直，相对于O1点的距离用h表示。平移该垂面到O1点的距离，当h等于铰链高度再加上斜支臂后端板的厚度时，即是斜支臂后端板所在平面。与上支臂中心平面eO1OFE交于eEF直线，e为上支臂中线在后端板上的交点。ed连线即是后端板平面上、中支臂截面中心的连线。

在后端板平面内，水平中心线在dD直线上。过d点作dF的垂线与eEF的延长线交于g点，得到gd直线，即是后端板的垂直中心线。下面求证这几个平面构成的角度关系。

在△edF中，设∠deF＝∠4，∠edF＝∠5，根据正弦定理得：

dF/sin ∠ 4 ＝ ed/sinφ1，

将（6）、（7） 代 入 上 式 得：sin ∠ 4 ＝ sinφ1/（tanθ1×tanα）

∠4＝sin-1[sinφ1/（tanθ1×tanα）]

在△edF中，∠5＝180°-∠4-φ1，∠5即为后端板平面内上中支臂中心连线与后端板水平中线的夹角。

又因为gd⊥ dF，∠gde＝∠4+φ1-90°，∠ gde即为后端板平面内上中支臂中心连线与后端板垂直中线的夹角。设定∠gde＝η1则得出如下表达公式：

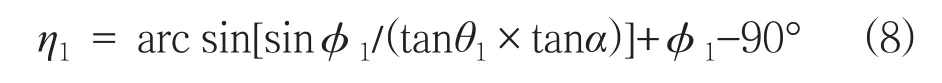
将此公式命名为：后端板平面内，上、中支臂中心连线与后端板垂直中线的夹角公式。同理可以求证出，在后端板平面内：下、中支臂中心连线与后端板垂直中线的夹角公式：

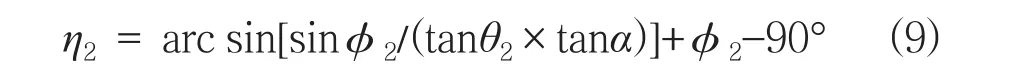
上述公式，只是弧形闸门三叉斜支臂扭角计算的一种派生公式。提出这个公式的意义在于，更详细的说明与V型斜支臂存在的不同之处：在V型斜支臂的后端板平面内，该角度与扭角是同一个值；三叉斜支臂则是不同值，也是容易出现错误的地方。

4 弧门三叉斜支臂扭角验算方法

将相关公式进行归纳，总结出弧形闸门三叉斜支臂扭角的验算步骤和方法。

使用的前提条件：弧形闸门采用三叉斜支臂结构类型时，当中支臂作为弧门所受水压的合力方向，上、中、下支臂与主横梁水平连接且水平偏斜角相等时，以垂直于中支臂平面且与中支臂中线垂直的面，作为斜支臂后端板与支铰的分界面，在此种结构状态下适用。

三叉斜支臂的构造角度（见图3）：斜支臂水平偏斜角α；上、中支臂之间的夹角θ1，中、下支臂之间的夹角θ2；在支臂后端板平面，上支臂相对于中支臂的扭角φ1，下支臂相对于中支臂的扭角φ2；以及上、中支臂中心连线与后端板垂直中线的夹角η1，下、中支臂中心连线与后端板垂直中线的夹角η2。这四种角度之间存在必然的函数关系，使三叉斜支臂结构的相关尺寸与之对应。

图3 弧形闸门三叉斜支臂结构示意图

设定计算公式中：L1、L2-对应面板的外缘弧长；θ1、θ2- 斜支臂上中、中下支臂中线的夹角；θ1′、θ2′-斜支臂上中、中下支臂轴线在侧墙平面投影的夹角；η1、η2-上中、下中支臂中心连线与后端板垂直中线的夹角；R-弧门面板外缘半径，h-面板外弧到支臂前端板距离，L-支铰跨距，l-支臂前端板跨距。以上角度单位：（°）度，长度、距离单位：（mm）毫米。

（1）基本验算公式

斜支臂水平偏斜角计算公式：tanα=（L-l）/2（R-h）

面板弧长与斜支臂侧墙面投影的夹角计算公式：L1=θ1′×Rπ/180，L2=θ2′×Rπ/180

斜支臂夹角与侧墙面投影夹角的换算公式：

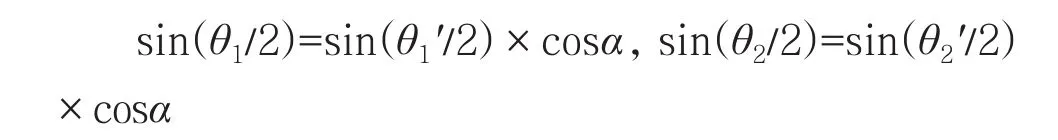
上述公式，也适用V型斜支臂。

（2）三叉斜支臂扭角计算公式

上支臂腹板中线相对于中支臂腹板中线的扭角公式：tanφ1＝ sinα×tanθ1′；

下支臂腹板中线相对于中支臂腹板中线的扭角公式：tanφ2＝ sinα×tanθ2′。

（3）支臂后端板平面，上、下支臂与中支臂中心连线夹角计算公式

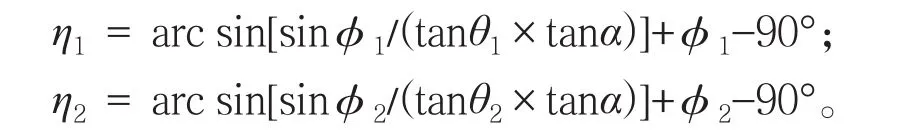
η1、η2是扭角的一种变形，或者说，是同一角度在不同位置的显示值。在三叉斜支臂的制作和检测过程中，后者比前者更实用。

5 三叉斜支臂的结构特点

当设定三支臂水平偏斜角α相同的条件下，三叉斜支臂的上、中、下支臂的中线并不处在同一个平面内，而是组成一个圆锥弧面，上中、中下支臂中线分属于2个平面。可以这样理解：如果将弧门门叶视作车轮轮圈的一部分，支铰视作轮箍的话，上、中、下支臂中线可以看作斜向外侧的三根辐条，呈现伞骨状分布。

图4是三叉斜支臂的三维线框：如果将中支臂调整到与上下支臂夹角相等位置：BO1、AO1、CO1分别代表三叉斜支臂的中线，与侧墙的夹角相等；A′O1是上、下支臂的平分线，明显看出A′O1与AO1并不相同，说明了三叉斜支臂与V型斜支臂两种结构的不同。

图4 三叉斜支臂三维线框

如果将中支臂布置到“上、下支臂夹角平分线上”形成三叉斜支臂：会产生中支臂前端跨距不等于上、下支臂；且中支臂长度、水平偏斜角也不相等；如果强制将中支臂移动到水平偏斜角与长度相等，保持原支臂后端板位置不变，又会造成原后端板不垂直于中支臂中线，这样就违背现行《规范》“在平分线的垂直剖面上”的条件；如果后端板与中支臂中线保持垂直一起移动，就转化成本文所论述的三叉斜支臂结构类型。

通过以上分析可以认清：所提出的“弧门三叉斜支臂扭角验算方法”是《规范》的“6.1.11”条款的延伸与发展。

6 实施效果检验

6.1 原图纸设计数据

洪都拉斯PATUCAⅢ水电站溢洪道14m×22m×21.5m表孔弧门，是三叉斜支臂弧形闸门。图纸设定的斜支臂水平偏斜角a=3.9362°，上中支臂的夹角θ1＝ 15.8036°，中下支臂的夹角θ2＝ 11.1357°，图纸给出在支臂后端板平面上的扭角φ1=1.1598°，φ2=0.7909°。扭角值为套用规范“6.1.11条款计算公式”得出，进行计算可以证明。

6.2 图纸扭角的验算

对此类型弧形闸门框架结构布局进行分析，符合上述标题“4”验算方法使用条件，运用总结的方法加以验证。不要局限图纸设定的角度，在弧门结构中，角度只是表示相互位置，因为角度与尺寸单位误差的不同，如果水平偏斜角相差0.001°，该弧门斜支臂前端板跨距就会产生0.88mm误差，这是安装定位螺栓绝对不允许的。所以，依据基本尺寸对所有角度进行计算，是得出正确结论的前提条件。

L=12000mm，l=8537.58mm，h=1840mm，R=27000mm，L1=7465mm，L2=5260mm。代入“本文 4（1）”条公式计算得出：α＝ 3.936205413°（三维软件自动显示科学数据，为了与实测结果一致，尽可能保留多位小数），θ1′＝ 15.841222°，θ2′＝11.16206668°。

将计算得出角度参数代入上述推出的三叉斜支臂扭角计算公式：

得 出 的 结 果：φ1＝ 1.115873729°，φ2＝0.776023576°；

继续代入上、下支臂与中支臂中心连线夹角计算公式：

得 出 的 结 果：η1＝ 0.547189252°，η2＝0.384319474°；

6.3 三维模型自然生成的扭角检测

单凭一个计算结果，还不足以认定图纸错误。下面采用Autodesk inventor软件建立弧门斜支臂的三维模型，通过模型在立体空间自然形成的角度加以验证。详见图5和图6。

图5 三叉斜支臂三维模型

为了简化视图，模型省略了支柱间连接撑杆，加大了支铰到后端板的距离，省略了斜支臂的裤衩部份，这些改变不会影响角度。通过图6可以看出三维模型得到的上、下扭角φ1＝1.11587°、φ2＝0.77602°，η1＝ 0.54719°，η2＝ 0.38432°与计算结果一致。空间的立体模型验证了三叉斜支臂扭角计算公式的正确性。

7 结语

对三叉斜支臂结构存在的模糊认识，并非简单的只是个别图纸错误。甚至一些带有严重错误的专业论文在刊物上出现。例如：张峰水库溢洪道三支臂弧形钢闸门由山西某地方水利设计院设计，同样出现生硬套用规范计算斜支臂扭角的现象，论文（百度可以找到）介绍的计算结果φ＝1.136°；采用本文“验算求证方法”的计算值是φ＝1.114°。

图6 三叉斜支臂三维模型后端板投影截屏

该项技术涉及弧形闸门设计与制作的基础理论，以及对规范条款的理解和澄清。推广应用后能提高行业技术水准、减少不必要的设计错误发生，避免了制造组拼过程中因扭角错误造成的返工和材料浪费。鉴于弧门扭角错误重复出现，有必要《规范》修订时，将“验算求证方法”作为补充条款备注。为标准的形成提供了理论准备和资料支持。