隧洞开挖过程中锚固支护施加时与掌子面距离的确定

白 琦,肖 明

(武汉大学水资源与水电工程科学国家重点实验室,湖北武汉430072)

隧洞开挖过程中锚固支护施加时与掌子面距离的确定

白 琦,肖 明

(武汉大学水资源与水电工程科学国家重点实验室,湖北武汉430072)

基于三维弹塑性损伤有限元分析软件,建立了某引水隧洞工程的三维有限元模型,首先确定了施加锚固支护时的开挖荷载释放率；然后分别研究了随开挖荷载释放率增大和掌子面推进时围岩的变形规律,并基于开挖荷载释放率与位移释放率之间的关系及位移释放率与监测断面至掌子面距离之间的关系,建立了开挖荷载释放率与监测断面至掌子面距离的关系,确定了以施加支护时与掌子面的距离为参数的锚固支护时机。

隧洞；开挖荷载释放率；位移释放率；锚固支护时机

隧洞开挖过程中受围岩材料、地应力及施工扰动等因素的影响,合理地选择锚固支护时机是个十分重要的问题,支护过早,则不能充分发挥围岩的承载能力,使得锚杆受力过大,支护太晚,则围岩变形太大,可能引起围岩失稳。对于隧洞开挖过程中的围岩变形和支护时机问题,许多学者进行了广泛而深刻的研究。赵旭峰[1]等结合数值计算结果和现场实测数据,分析了深部软岩隧道施工性态时空效应；周顺华[2]在明确应力释放率和位移释放率的基础上,重点分析了开挖面空间效应区的位移释放,并建立了应力释放与位移释放间的关系；李术才[3]进行了数值模拟和模型试验,定义了断面综合荷载释放率和荷载释放差异系数来研究隧道施工断面综合荷载释放过程；李利平[4]研究了隧道软弱破碎围岩空间变形机制与荷载释放演化规律；孙均[5]等论述了采用释放荷载模拟隧洞开挖的有限元步骤,并采用广义虚拟支撑力法模拟开挖面时空效应；苏凯[6]等给出了隧洞开挖过程中初次支护时机的选择方法；肖明[7]等研究并提出了地下隧洞开挖和支护的三维数值计算方法。

本文基于三维弹塑性损伤有限元分析软件[8],建立了某引水隧洞工程的三维有限元模型,分别研究了随开挖荷载释放率增大和掌子面推进时围岩的变形规律,构建了开挖荷载释放率η与位移释放率ξ之间的关系及位移释放率ξ与监测断面至掌子面距离D之间的关系,探求了开挖荷载释放率η与监测断面至掌子面距离D之间的关系,从而得到了施加锚固支护时与掌子面的距离的确定方法,并在拟定的锚固支护时机下,进行了锚固支护效应分析。

1 隧洞开挖及支护方法和掌子面空间效应

1.1 三维非线性有限元的隧洞开挖及支护方法

隧洞开挖以后,由于开挖单元的参数被弱化成为空气单元,因此围岩会受到开挖释放荷载的扰动作用[9]。开挖释放荷载{Fc}是指作用于围岩节点上的初始地应力的释放,可按下式计算

(1)

式中,{σ0}为开挖单元初始地应力矩阵；[B]T为单元应变矩阵的转置。由于开挖释放荷载一般由围岩与支护结构共同承担,因此可将开挖释放荷载{Fc}分为两部分,分别进行有限元迭代计算,即

{Fc}=η{Fc}+(1-η){Fc}

(2)

式中,η为荷载释放率。

采用M-C屈服准则,在尚未支护前,将第一部分荷载η{Fc}加于围岩单元上,然后按下式进行非线性迭代

[Ke]{δ}i=η{Fc}+[Kp]{δ}i-1

(3)

式中,[Ke]为岩体单元弹性刚度矩阵；[Kp]为岩体单元塑性刚度矩阵。

η{Fc}迭代计算完成后,考虑锚固支护。采用隐式锚杆柱单元方法[10]模拟锚杆,将锚杆单元的刚度矩阵添加到岩体单元上,重新形成岩体单元的等效刚度矩阵。对第二部分荷载(1-η){Fc}按下式进行迭代计算

[Ke]{δ}i=(1-η){Fe}+[KP]{δ}i-1

(4)

1.2 荷载释放率的确定方法

隧洞开挖完成后,其单元应力状态可以根据下式分为弹性和塑性,即

(5)

式中,F为屈服函数；{σc}为隧洞开挖后的围岩应力；{σ0}为岩体初始地应力；{Δσ}为隧洞开挖后作用在围岩上的单元应力增量。若围岩单元的初始应力状态为弹性,开挖后进入了塑性状态,那么就会有一个临界状态,使得

F({σc})=F({σ0}+α{Δσ})=0

(6)

式中,α为单元的弹性系数,其大小反映了使单元进入临界状态时所需要的应力增量{Δσ}的比例。若开挖后围岩单元应力状态仍为弹性,则弹性系数α=1；若开挖前围岩就已经屈服,则α=0。岩石是一种弹塑性损伤介质,弹性荷载在隧洞开挖后便瞬间释放完成。考虑充分发挥围岩的承载能力及锚固支护发挥作用的滞后效应,因此认为锚固支护只能承担部分塑性荷载。故将弹性系数α适当放大得到开挖荷载释放率η,即

η=(1+β)α

(7)

式中,β为反映围岩承担塑性荷载的系数,取值范围一般为0<β<1,围岩岩性越好,则β越大；反之,β越小。β的确定和围岩岩性、地应力水平、隧洞形状、隧洞尺寸、施工方式等有关,需根据工程具体情况而定。在本文的例证工程中基于开挖荷载释放后期隧洞围岩位移增量迅速增大时围岩有失稳趋势,给出了β的估计值。

1.3 掌子面空间效应与位移释放率

在开挖过程中隧洞围岩的变形具有时空效应特征,空间效应是指隧洞开挖过程中掌子面对开挖后洞壁变形的约束作用[6],时间效应是指围岩变形随时间而改变；空间效应主要体现在刚开挖后围岩的急剧变形段,时间效应则表现在围岩的流变阶段。由于锚固支护一般在开挖后不久的时间段内施加,时间效应的影响很小,故在本文中计算围岩变形时只考虑开挖掌子面的空间效应。

在隧洞毛洞开挖过程中,考虑非坍塌情况,假定当掌子面通过洞周Z点的距离大于S后,Z点所发生的位移为US(∞,Z),而当该点与掌子面的距离D小于S所发生的位移为UD(D,Z),则定义Z点的位移释放率为

(8)

式中,ξ反映了开挖面对洞壁围岩变形的空间约束程度；S为开挖面空间效应影响范围,已经证实,S一般取距开挖掌子面2～3倍洞径的距离。

2 有限元模型分析

2.1 三维数值模型

某引水隧洞工程的洞型为圆形,洞径9.6 m,取X轴沿洞轴线指向开挖前进方向,范围为-50～50 m,长100 m；Y轴垂直于X轴,正向在开挖前进方向左侧,范围为-60～60 m,长120 m；Z轴与大地坐标重合,由-50 m高程延伸至380 m地面高程。建立的三维网格模型如图1a所示,模型共剖分了338 560个六面体单元,包含350 406个节点。地勘资料表明,隧洞围岩为Ⅲ1类花岗岩,岩体物理力学参数取值见表1。根据实测地应力值进行初始地应力场反演,取监测点位置如图1b所示,1、3号监测点在地应力第一主应力方向上,2、4号监测点在地应力第三主应力方向上,监测断面取在X=0断面。

表1 岩体物理力学参数取值

图1 三维数值模型与监测点位置

2.2 锚固支护时荷载释放率的确定

先对三维有限元模型一次完全开挖,得到开挖荷载的等效节点力,然后根据荷载释放率将等效结点力按比例分为20份(每份为5%),依次施加在围岩单元节点上,分别统计各荷载释放率下4个监测点的位移。

采用塑性区体积率和位移增量来反映围岩特性的变化过程：塑性区体积率为围岩塑性区体积与岩体开挖体积之比；位移增量为某一荷载释放率下的围岩位移减去前一荷载释放率下的围岩位移。结果如图2和图3所示。

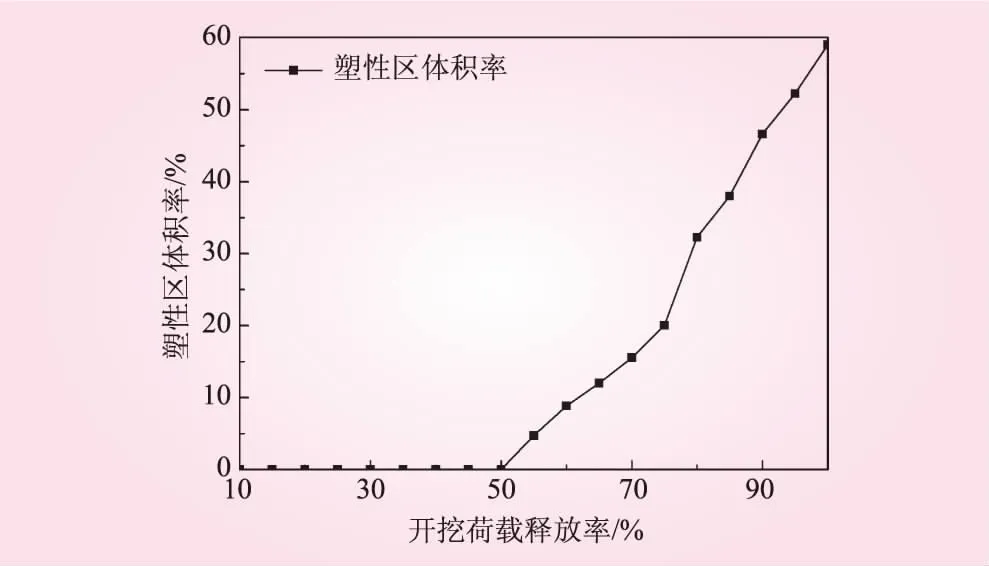
图2 围岩的塑性区体积率

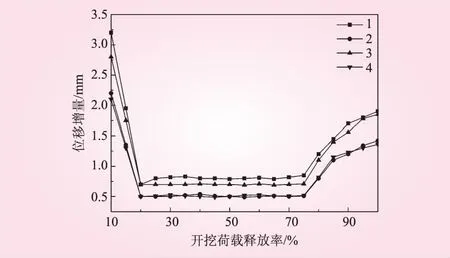
图3 围岩的位移增量

从图2可以看出：荷载释放率为50%时,塑性区出现,说明单元的弹性系数可取0.50左右；此后塑性区随荷载释放率的增加而增大,在荷载释放率为75%以后,塑性区增加速率加快。

从图3可以看出：随着开挖荷载释放率的提高,围岩位移不断增大；在开挖荷载刚开始释放的时候位移增量最大,荷载释放率为20%～75%时位移增量基本不变,围岩位移稳定增大,之后随着荷载释放率进一步增加(75%～100%),围岩位移增量又开始增大,表明随着开挖荷载释放率的增加,围岩位移快速增大,可能出现失稳现象。文献[11-12]研究表明,在开挖荷载释放后期,当围岩位移变化速率迅速增大时,为了防止围岩失稳,应当及时施加支护措施。因此取β=0.50,由式(7)可知,施加锚固支护时的荷载释放率为η=(1+β)α=(1+0.50)·0.50=75%。综合以上分析,可取开挖荷载释放率为75%时为最佳锚固支护时机。

2.3 开挖过程中围岩变形状态

将三维有限元模型进行全断面逐段开挖(以2.5 m为进尺),记录开挖过程中各测点的围岩位移变化,并计算围岩位移增量,结果如图4和图5所示。

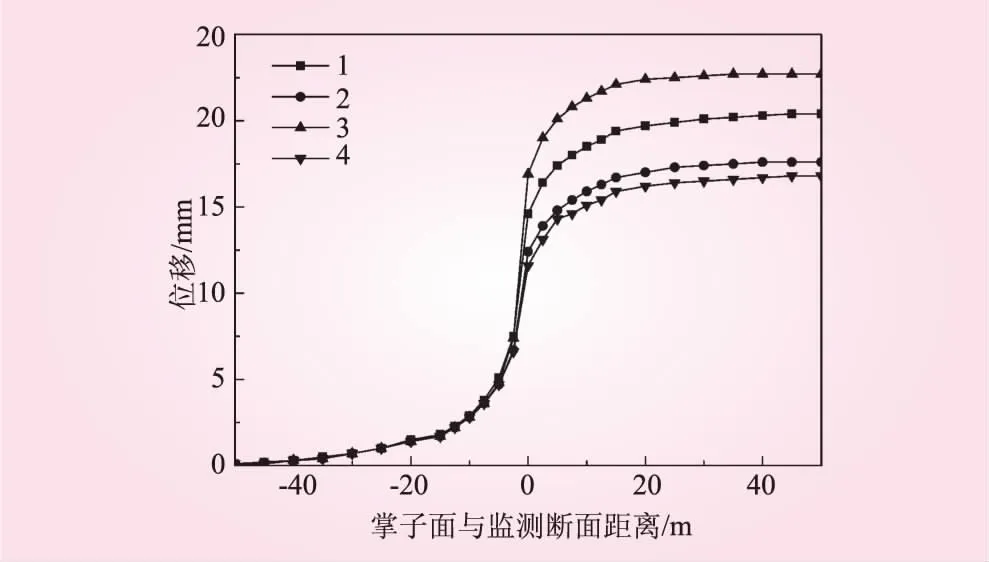
图4 开挖推进过程中的围岩位移

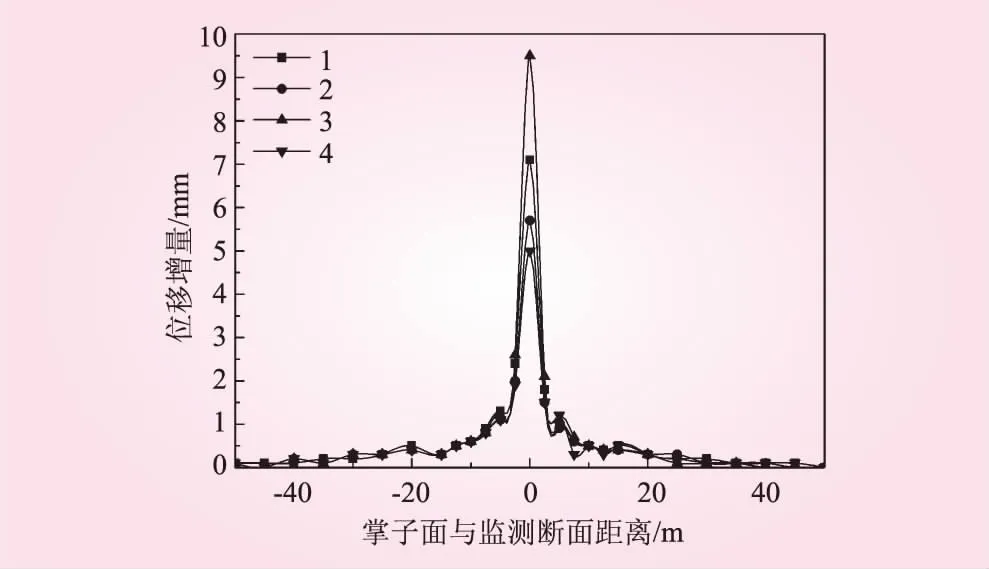
图5 开挖推进过程中的围岩位移增量

结合图4和图5可以得到：在开挖掌子面到达监测断面之前,该处围岩已经有了先行位移；从掌子面靠近监测断面约1.5倍洞径处开始,监测点围岩位移值迅速增大；当掌子面通过监测断面时,位移增量有最大值,且远远大于其他开挖时期的位移增量,说明这一时期开挖荷载的释放很大；然后随着掌子面经过监测断面后继续推进时,该处围岩位移继续增加但位移增量迅速减小；当掌子面远离监测断面2倍洞径以上距离时,监测点围岩位移变形基本趋于稳定。

3 锚固支护施加时距掌子面距离的确定

已经给出了随着掌子面推进三维模型监测点Z的位移释放率ξ(D,Z)的计算公式,这里引出不同荷载释放率下三维模型监测点Z的位移释放率ξ(η,Z)的计算公式

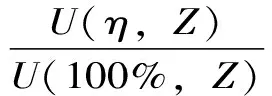
(9)

式中，U(η,Z)为荷载释放率为η时Z点的位移；U(100%,Z)为开挖荷载完全释放时Z点的位移。

根据式(8)、(9)定义的位移释放率,计算出不同荷载释放率下三维模型监测点的位移释放率ξ(η,Z)和随着掌子面推进三维模型监测点的位移释放率ξ(D,Z)。易知ξ的取值范围为[0,100%]且连续,则必然存在

ξ(η,Z)=ξ(D,Z)

(10)

由式(10)可知,对于给定的位移释放率ξ,必有唯一的荷载释放率η和掌子面与监测断面之间的距离D与之对应。因此,以位移释放率ξ为横坐标,掌子面与监测断面之间的距离D为主纵坐标,荷载释放率η为次纵坐标,建立荷载释放率η与掌子面与监测断面D之间的距离之间的对应关系,如图6所示。

图6 基于位移释放率 ξ的 η-D曲线

由图6可知,若已知荷载释放率η,则可求得掌子面与监测断面之间的距离D。具体方法如下：①根据3.2确定的施加锚固支护时的荷载释放率75%,在次坐标轴上找到η=75%的点；②在根据三维模型建立的开挖荷载释放率η与位移释放率ξ的关系曲线上,找到该荷载释放率对应的位移释放率ξ(75%,Z)；③由于位移释放率轴为公共水平轴,因此可在根据三维模型建立的位移释放率ξ与监测断面至掌子面距离D之间的关系曲线上找到一点使得ξ(D,Z)=ξ(75%,Z),过该点作水平线与主纵坐标轴垂直相交,交点的坐标即为最佳支护时机下施加支护时与掌子面的距离D。

由于随着荷载释放,4个测点的位移释放不是完全一致的,因此图6中确定的距离D各不相同。其中,测点1、2、3、4确定的支护施加距离分别为5.77、6.17、4.78、6.55 m。选取最危险的情况,即最佳锚固支护时机下施加支护时与掌子面的距离不能超过4.78 m。

4 结 论

(1)随着荷载释放率的增加,围岩塑性区从无到有,逐渐增大；荷载刚开始释放时围岩位移增量最大,然后基本保持平稳,在荷载释放的末期,位移增量又开始迅速增大,表明围岩有失稳趋势。开挖掌子面推进时,在掌子面到达监测断面之前,监测断面处已经有了超前位移；掌子面距监测断面越近,围岩位移增量越大；掌子面通过监测断面时,围岩位移增量达到最大；掌子面通过监测断面之后继续推进,该处位移继续增大直至趋于稳定。

(2)以某引水隧洞工程为例,由围岩塑性区出现时的荷载释放率得出弹性系数为0.5,又由荷载释放末期位移增量开始迅速增大,确定开挖荷载释放率为75%时为最佳锚固支护时机；根据位移释放率ξ的概念,建立了荷载释放率η与位移释放率ξ之间的关系及位移释放率ξ与掌子面至监测断面距离D的关系,得到了以距离D为参数的支护时机的确定方法,得出距掌子面4.78 m时施加支护为最佳锚固支护时机。

[1]赵旭峰, 王春苗, 孔祥利. 深部软岩隧道施工性态时空效应分析[J]. 岩石力学与工程学报, 2007, 26(2): 404- 409．

[2]周顺华, 高渠清, 崔之鉴. 开挖应力释放率模型[J]. 上海力学, 1997, 18(1)： 91- 98．

[3]李术才. 超大断面铁路隧道施工断面综合荷载释放过程研究[J]. 岩土力学, 2011, 32(9)： 2845- 2851．

[4]李利平. 超大断面隧道软弱破碎围岩空间变形机制与荷载释放演化规律[J]. 岩石力学与工程学报, 2012, 31(10)： 2109- 2118．

[5]孙钧, 朱合华. 软弱围岩隧洞施工性态的力学模拟与分析[J]. 岩土力学, 1994, 15(4)：20- 33．

[6]苏凯, 崔金鹏, 张智敏. 隧洞施工开挖过程初次支护时机选择方法[J]. 中南大学学报： 自然科学版, 2015, 46(8): 3075- 3082．

[7]肖明. 地下洞室施工开挖三维动态过程数值模拟分析[J]. 岩土工程学报, 2000, 22(4)： 421- 425．

[8]肖明, 叶超, 傅志浩. 地下洞室开挖和支护的三维数值分析计算[J]. 岩土力学, 2007, 28(12)： 2501- 2505．

[9]张雨霆, 肖明, 汤福平. 深埋地下洞室群轴线方位合理布置的计算分析[J]. 武汉大学学报： 工学版, 2009, 42(3): 331- 335．

[10]肖明. 地下洞室隐式锚杆柱单元的三维弹塑性有限元分析[J]. 岩土工程学报, 1992, 14(5): 19-26．

[11]关宝树, 赵勇. 软弱围岩隧道施工技术[M]. 北京: 人民交通出版社, 2011．

[12]赵勇. 隧道软弱围岩变形机制与控制技术研究[D]. 北京： 北京交通大学, 2012: 95- 107．

(责任编辑焦雪梅)

《光伏发电工程预可行性研究报告编制规程》和《光伏发电工程可行性研究报告编制规程》送审稿通过审查

2017年4月26日～27日，《光伏发电工程预可行性研究报告编制规程》和《光伏发电工程可行性研究报告编制规程》送审稿通过水电水利规划设计总院(以下简称水电总院)审查。

《光伏发电工程预可行性研究报告编制规程》和《光伏发电工程可行性研究报告编制规程》由水电总院、中国电建集团西北、中南、北京勘测设计研究院有限公司和中国水电顾问集团有限公司共同编制。两项标准编制工作于2014年8月启动。2015年6月组织召开了大纲评审会，2016年3月编制完成了两项标准征求意见稿，向行业广泛征求修改意见和建议。根据反馈意见，编制组反复修改完善，2016年11月组织召开了两项标准送审稿讨论会，根据讨论会意见，于2017年3月修改完成了送审稿。

会议审查认为，编制组提交审查的有关技术文件齐全；编制依据充分，结构清晰，用词简明，规定明确，与国内相关标准相协调，具有可操作性；两项标准格式规范，符合《工程建设标准编写规定》(建标〔2008〕182号)的规定。有利于规范光伏发电工程预可行性研究报告和可行性研究报告的编制，达到国内先进水平。会议要求编制组根据本次审查会议意见，对两项标准送审稿进一步修改完善，适时召开定稿会，形成报批稿，尽早报国家能源局批准发布实施。

两项标准规定了光伏发电工程预可行性研究报告和可行性研究报告编制的原则、内容、深度和技术要求，适用于新建、改建或扩建的并网光伏发电工程的预可行性研究报告和可行性研究报告的编制。两项标准是在广泛调研、认真总结我国光伏发电工程预可行性研究阶段和可行性研究阶段的技术要求、实践经验及研究成果的基础上，广泛征求各方意见，经反复讨论、修改和完善而形成的，充分反映了光伏发电工程预可行性研究阶段和可行性研究阶段的特点和技术水平。两项标准的制定对合理开发太阳能资源、保证光伏发电工程建设有序开展具有重要意义。

(冷 辉)

DeterminationoftheDistancefromTunnelFacetoAnchorSupportingWorkingFaceduringTunnelExcavation

BAI Qi, XIAO Ming
(State Key Laboratory of Water Resources and Hydropower Engineering Science,
Wuhan University, Wuhan 430072, Hubei, China)

Based on 3D elasto-plastic damage finite element analysis software, a three-dimensional finite element model of a diversion tunnel is established to determining the distance from tunnel face to anchor supporting working face during tunnel excavation. Firstly, the excavation load releasing rate at the time of anchor supporting is determined. Secondly, the deformation values of surrounding rock are studied respectively with the increase of excavation load releasing rate and the advancing process of tunnel face. Thirdly, based on the relationship between excavation load releasing rate and displacement releasing rate and the relationship between displacement releasing rate and the distance between tunnel face and monitoring section, the correlativity between excavation load releasing rate and the distance between tunnel face and monitoring section is built, thus the anchor supporting time by using the distance from tunnel face to anchor supporting working face as a parameter can be determined．

tunnel; excavation load releasing rate; displacement releasing rate; anchor supporting time

2016- 12- 12

国家自然科学基金项目(51579191)；国家重点基础研究“973”计划项目(2015CB057904,2015CB057900)

白琦(1993—),男,甘肃会宁人，硕士研究生,研究方向为地下结构工程；肖明(通讯作者)．

TU45

：A

：0559- 9342(2017)06- 0065- 05