基于改进的集对分析方法在河流健康评价中的应用
舒持恺,杨 侃
(河海大学水文水资源学院,江苏南京210098)
基于改进的集对分析方法在河流健康评价中的应用
舒持恺,杨 侃
(河海大学水文水资源学院,江苏南京210098)
考虑到河流健康评价系统中存在的不确定性问题,引入集对分析理论(SPA),并改进其联系度的计算,以灰色聚类理论中的不同灰类的聚类系数取代相应的联系度分量;同时针对传统灰色聚类理论中的白化函数覆盖范围小的问题,用改进的指数型白化函数建立样本等级对应关系,并利用两阶段层次分析法(AHP)进行指标权重的计算。以某市河流H为例对建立的评价指标、评价标准和评价方法进行了验证应用,结果显示该方法能够很好地处理评价体系中的不确定性和复杂性因素,适用于河流健康评价。
河流健康评价;改进白化权函数;集对分析理论;层次分析法;不确定信息
0 引 言
健康的河流不仅需要保持生态学意义上的完整性,还应强调对社会服务功能的发挥[1-2]。当前河流健康评价方法很多,各有各的利弊。鉴于河流本身存在的许多不确定性因素,引入集对分析理论(SPA),可以很好地处理河流评价系统中不确定性问题[3]。但传统的集对分析理论中联系度计算过于简单,本文引入灰色聚类理论,以不同灰类的聚类系数表示相应的联系度分量。同时,针对传统灰色聚类法的白化函数覆盖范围小的问题,做出改进,用指数型白化函数建立样本值与各等级之间的对应关系,充分利用已知信息淡化未知信息,客观真实地反映系统本质[4];并用改进层次分析法(AHP)进行指标权重的计算;最后,通过实例验证了该方法的可行性和合理性。
1 构建河流健康评价指标体系
在进行河流健康评价之前,需筛选出评价指标,要求能够准确客观地反映出河流生态环境状况及变化趋势。主要从三方面考虑:①评价指标的独立性;②从定性方面最能反映河流健康的程度指标(专家咨询、群众问访);③指标数据可以实测取得。本文依照相关原则,经综合考虑某市河流基本情况,从自然环境子系统和社会服务子系统进行评价指标筛选,从而建立了四层指标体系[1-2,5](见表1)。

表1 河流健康评价体系层次划分
准则层部分指标含义的说明如下:
(1) “河岸稳定性”指标D1定义为稳定无明显侵蚀的河岸线长度占河岸线总长度的比例,;“稳定无明显侵蚀的河岸”包括有良好植被覆盖的自然土质岸坡及人工护坡如浆砌石、混凝土岸坡。
(2)“生态流量满足程度指数” D3是指河流控制断面或特征断面对河流最小生态需水量的满足程度。
(3)“公众满意度”D9是指公众对评价河流景观、美学价值及其他综合服务功能的满意程度。采用公众参与调查统计方法进行。
(3)“水功能区水质达标率” D11这一指标可以反映河流对饮用水水源地、渔业养殖、工业、农业、景观娱乐等供水功能的水质满足情况。
本文将指标等级分为优、良、中、差4个级别(见表2)。等级标准以文献[5]为参考。
2 引入灰色聚类理论改进集对分析方法
2.1 集对分析理论(SPA)
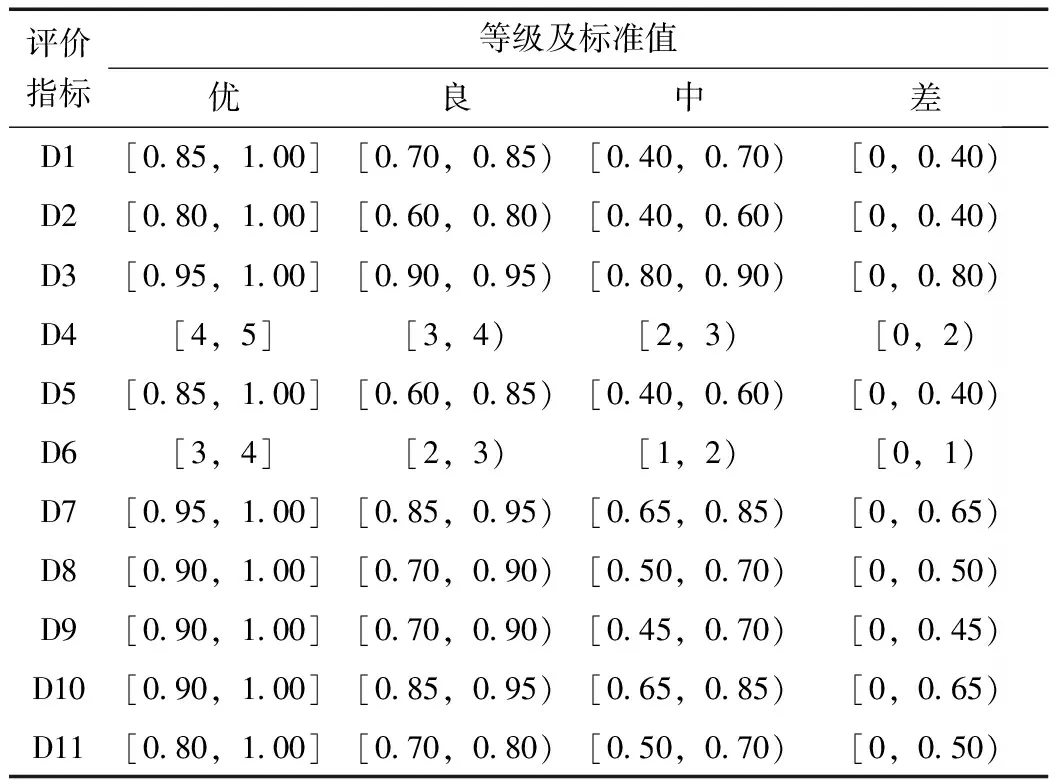
表2 评价指标等级划分标准
集对分析理论是我国学者赵克勤于1989年提出的一门处理不确定性问题的系统理论方法。它把研究的问题构建具有一定联系的两个集对,对集对中两集合的特性进行同一、差异、对立的系统分析,然后用联系度μ表达式定量刻画[6-7]。对于各评价指标,可用下述公式计算联系数。即
μk=ak+bki1+cki2+dkjk=1,2,…,n
(1)
ak+bk+ck+dk=1ak、bk、ck、dk∈[0,1]
(2)
式中,ak、bk、ck、dk称为联系度分量;ak反映了指标k对等级优的偏向度;bk反映了对等级良的偏向度;ck反映了对等级中的偏向度;dk反映了对等级差的偏向度。可取i1=0.33,i2=-0.33、j=-1,则各指标k的四元联系数μk取值在[-1,1]之间,评判标准如表3。

表3 联系数 μk的评价标准
对于河流健康评价中n个指标体系,分析步骤如下:
(1)根据样本数据,按式(3)计算各个指标的四元联系数μk,并按照表3的标准进行判断,得到河流各个指标k的评价等级
ak=μk1,bk=μk2,ck=μk3,dk=μk4
(3)
式中,μk1、μk2、μk3、μk4分别是指标k对应的4种不同灰类等级下的聚类系数。
(2)结合各个指标的权重,对n个指标的联系数μk进行加权平均,按下式计算得到总体联系数μ,再对其进行分析总结。即
(4)
式中,ωk为指标k的权重。本文通过改进的层次分析法计算得到。
2.2 改进集对分析方法
结合集对分析理论与灰色聚类法,采用优、良、中、差4个灰类分级标准,并将指标相应的聚类系数按式(3)取代联系度分量。
传统聚类白化函数采用“升降半梯形”结构,只考虑了相邻等级评价值的影响,如果评价值在相邻等级以外,其白化函数值便为零,当样本数据过于分散时,可能会丢失很多重要信息,使评价结果出现误差[8-10]。因此,本文构造指数型白化函数,改进后的函数曲线是平滑的,扩大了函数覆盖范围,有效解决了零权重问题。
定义ykp是指标k隶属于灰类等级p的评价标准值,每个指标有m个灰类等级,xqk是样本q对应于指标k的样本数据值,fkp(xqk)是样本q的指标k隶属于灰类等级p的白化函数,则相应的白化函数值计算式
(5)
(6)
(7)
对应的白化函数图像如图1所示。其中,图 a、b、c分别对应于白化函数表达式(5)、(6)、(7)。

图1 指数型白化函数图像
利用式(5)~(7)计算得到各指标在不同灰类等级下的聚类系数,再对其进行归一化处理。即
(8)
再由式(3)即可得到改进后的联系度分量。由于引入指数型白化函数,使得联系度分量的计算更为合理,比较好地体现了各个指标等级间的相互联系。
2.3 计算指标权重
本文通过二阶段层次分析法(AHP)进行指标权重的计算。传统的(1~9)九标度法,专家和决策者很难掌握标度的标准,尤其是当比较指标过多时,更容易产生混乱,从而判断矩阵一致性效果较差。因此,本文采用构造矩阵的两阶段法[11]:第一阶段,采用容易判断的的(0,1,2)三标度法来对每一个元素进行两两比较后,建立一个比较矩阵;第二阶段,通过变换将比较矩阵转化为判断矩阵,并进行一致性检验。具体步骤如下:
(1)将研究问题进行分层,建立递阶层次结构,清楚地表明各层次之间的关系。
(2)用三标度法对同一层元素进行两两比较后建立比较矩阵An×n。
(4)由判断矩阵得出权重ω,并检查判断矩阵Cn×n的一致性是否可以接受。
2.4 改进集对分析方法计算流程图
为了直观地描述计算方法过程,绘制了改进集对分析方法计算流程图(见图2)。

图2 计算流程示意
3 实例应用
河流H贯穿某市南北,河道长约23.6 km,是省水系规划中确定的区域骨干4级河道,是该市主要航道之一;同时对南北河道水位起着很重要的调节作用。随着上游地区和该市相关镇区工业化和城市化步伐加快,在自然与人类活动双重胁迫作用下,该河流健康状况受到一定程度的影响,需要对其健康情况做出评价。数据资料来自现场调研、采样以及当地水利农机局部门提供。在实地调研过程中,将河流分段,设置检测取样断面,全程踏勘,一定程度上保证了资料的可靠性。将获取到的数据资料,应用上述指数型白化函数方法计算,得到2015年该河流11项指标的四元联系数,并进行分析,结果见表4、图3和图4。
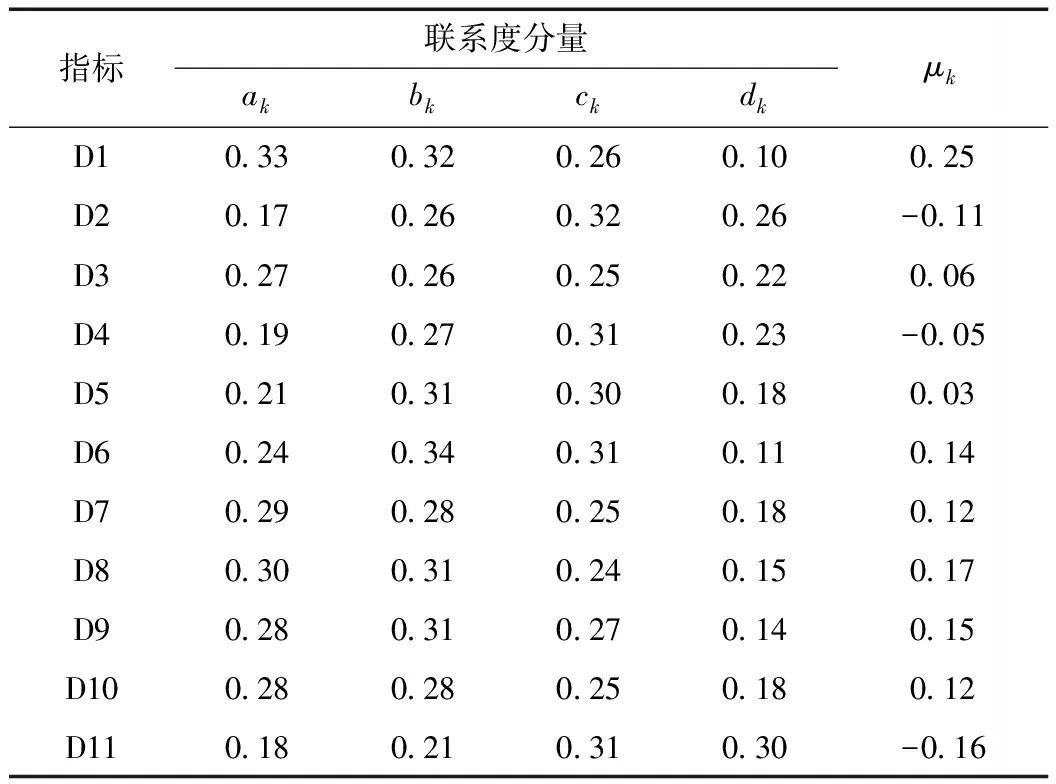
表4 河流健康指标评价结果
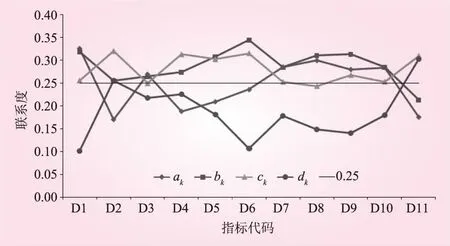
图3 各指标四元联系度分量

图4 各指标综合联系数 μk
由表4、图3、4可以看出:
(1)各指标的联系度分量ak,它体现的是该指标偏向等级优的程度。其中河岸稳定性指数(D1)、生态流量满足程度指数(D3)、防洪工程达标率(D7)、岸线利用管理指数(D8)、公众满意度(D9)、供水量保证率(D10)的ak值达到0.25(四元联系数的平均值)以上,表明该河流在这些方面状况优良。
(2)各指标的联系度分量dk,它体现的是该指标偏向等级差的程度。其中,河流流动性指数(D2)、水功能区水质达标率(D11)的dk值超过了0.25,生态流量满足程度指数(D3)、水质综合指数(D4)的dk值接近0.25,说明河流的流动性较差;同时水质存在污染情况。这也体现了河流的流动性与水体污染的关系,即流动性较差的河流往往容易受到污染。
(3)各指标的联系数μk,它体现的是该指标的总体水平。其中,河流流动性指数(D2)、水质综合指数(D4)、水功能区水质达标率(D11)的μk值小于零(等级良标准值),其余的指标均大于零。根据表3的标准划分,虽然河流的D2、D4、D11为中等水平,但对比其余的指标,也说明了该河流在流动性和水质方面有待改善。
根据改进的层次分析法进行11项指标权重的计算,得到权重值ω为[0.028,0.024,0.130,0.182,0.040,0.066,0.028,0.028,0.078,0.215,0.182]。结合表4中各指标的μk值,由式(3)求得河流总体的四元联系数μ值为0.029,由表3得到评价等级为中,与实际情况相符。
综上所述,H河2015年的评价等级为中等,健康状况较差,虽然能够较好地满足周边区域居民用水需求,但河流水质较差,流动性也不好,存在污染。今后,应当加大监管力度,控制河流污染,改善水质,恢复良好的水生态环境。同时河流两岸的防洪工程建设较好,应当充分利用好河流的防洪设施抵御洪水灾害。
4 结 语
(1)本文引入改进的指数型白化函数进行联系度的计算,克服了传统白化函数覆盖等级范围窄问题,准确包含了更多评价指标中的不确定信息;同时,利用二阶段层次分析法进行权重的计算,也比较方便合理。应用实例表明,该方法适用于河流健康评价。
(2)指数型白化函数虽然覆盖等级广,但函数曲线在相邻等级内下降较快,而在相邻等级之外趋于平缓,不知这样是否合理,还有待研究。
(3)河流健康评价的指标有很多,本文筛选的11个指标可能存在不足,今后还需深入研究探讨,逐步加以完善。
[1]耿雷华, 刘恒, 钟华平, 等. 健康河流的评价指标和评价标准[J]. 水利学报, 2006, 37(3): 253- 258.
[2]卞锦宇, 耿雷华, 方瑞. 河流健康评价体系研究[J]. 中国农村水利水电, 2010(9): 39- 42.
[3]王颖, 邵磊, 杨方廷, 等. 改进的集对分析水质综合评价方法[J]. 水力发电学报, 2012, 31(3): 99- 106.
[4]邓聚龙. 汉英对照灰色系统基本方法[M]. 2版. 武汉: 华中科技大学出版社, 2005.
[5]李浩, 杨侃, 陈静, 等. 灰色三角白化权集对分析模型在河流健康评价中的应用[J]. 水电能源科学, 2015, 33(8): 33- 36.
[6]赵克勤. 集对分析对不确定性的描述和处理[J]. 信息与控制, 1995, 24(3): 62- 166.
[7]赵克勤, 宣爱理. 集对论——一种新的不确定性理论方法与应用[J]. 系统工程, 1996, 14(1): 18- 23.
[8]马艳琴, 杨红艳, 潘平奇. 灰色聚类关联分析法的改进及其应用[J]. 数学的实践与认识, 2013, 43(19): 166- 172.
[9]胡军, 许丽忠, 张江山. 基于改进灰色聚类法的大气环境质量综合评价[J]. 福建师范大学学报: 自然科学版, 2012, 28(1): 49- 54.
[10]闫滨, 孙友良, 于保慧. 基于改进白化权函数灰色聚类法的水闸安全评价[J]. 沈阳农业大学学报, 2015, 4(2): 245- 249.
[11]朱茵, 孟志勇, 阚叔愚. 用层次分析法计算权重[J]. 北京交通大学学报, 1999, 23(5): 119- 122.
(责任编辑陈 萍)
RiverHealthAssessmentBasedonImprovedSetPairAnalysisMethod
SHU Chikai, YANG Kan
(College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China)
Considering the uncertainty problem in the assessment system of river health, the Set Pair Analysis (SPA) theory is introduced, and its connection degree calculation is improved by using the clustering coefficients of different grey classes in grey clustering theory to replace corresponding connection degree. At the same time, for solving the problem of small sample coverage of Definite Weighted Function in traditional grey clustering theory, the improved Definite Weighted Function of exponential type is used to set up sample level corresponding relation, and two-phase Analytic Hierarchy Process (AHP) is used to calculate index weight. The application of above method in River H verifies the index, criteria and method of assessment. The results show that the method can handle the uncertainty and complexity factors in assessment system well, and so it is suitable for river health assessment.
river health assessment; improved Definite Weight Function; Set Pair Analysis theory; Analytic Hierarchy Process; uncertain information
2016- 06- 14
国家重点基础研究发展973计划(2012CB417006);“十一五”国家科技支撑计划(2009BAC56B03)
舒持恺(1992—),男,安徽安庆人,硕士研究生,研究方向为水资源与水环境;杨侃(通讯作者).
X826
:A
:0559- 9342(2017)06- 0001- 04

