地震荷载作用下双面边坡稳定性数值模拟研究

刘思杰,刘明维

(重庆交通大学河海学院,重庆400074)

地震荷载作用下双面边坡稳定性数值模拟研究

刘思杰,刘明维

(重庆交通大学河海学院,重庆400074)

采用二维有限元程序PLAXIS-2D,系统地研究了地震条件下双面边坡的地震响应规律,计算了地震前后边坡的滑裂面和安全系数。结果表明,地震后,双面边坡仍处于稳定状态；较陡侧(左侧)边坡有明显的滑动趋势,并带动较缓侧(右侧)边坡上部岩体共同剪切滑动；左侧边坡塑性点分布范围明显扩大,并贯穿到右侧较缓边坡4/5高处,造成右侧边坡局部岩体拉断破坏；地震后边坡安全系数仅有1.08,稳定性较差,远小于地震前的1.32；地震前后边坡滑裂面基本相同。

地震荷载；双面边坡；稳定分析；PLAXIS-2D

0 引 言

2008年5月12日,四川省汶川县发生了8.0级大地震,强震不仅造成了大量的人员伤亡和财产损失,还诱发了数以万计的次生地质灾害,众多高陡边坡产生了奇特的动力特征[1]。地震往往导致边坡岩体破碎程度加重,内部塑性变形区范围扩大,其破坏机制变得更加复杂,如何定量评估地震作用下边坡的稳定性是当前地质灾害研究的热点和难点。

D. Leshchinsky等[2]采用拟静力法对R. Baker[3]提出的边坡稳定性静力计算方法进行拓展,用以评价地震动荷载作用下简单边坡的稳定性,并通过求解显式的所有静力平衡方程式得到潜在滑动面上的正应力分布,最终获得边坡的最小安全系数。H. I. Ling[4]将拟静力法用于沿节理面滑动的岩体地震稳定性分析中,进行了地震稳定分析和永久位移计算。E. Ausilio 等[5]将拟静力法应用于加固边坡的地震稳定分析中,提出了加固力计算公式及与地震力相关的屈服强度的表达式。李海波等[6]利用UDEC分析了地震荷载作用下坡高、坡度、岩层倾角以及地震波参数(振幅、频率等)对顺层岩质边坡安全系数的影响规律。肖锐铧等[7]通过模型试验研究了双面边坡在强震条件下的动力响应规律发现,强震条件下地震水平惯性力是导致边坡破坏的主要原因,在地震情况下边坡变形破坏表现出明显的初动破坏效应。杨长卫等[8]基于弹性波动理论,利用水平分层法,建立微元体的受力平衡微分方程,借助Hilbert-Huang 变换,应用振型分解法和正交理论推导双面岩质高陡边坡加速度高程放大效应的时频分析方法,并通过振动台试验和数值模拟验证该方法的合理性。

以往有关地震对边坡稳定性的影响研究主要针对单面边坡模型,仅考虑了地震对山体一侧边坡的影响[9-12],而真实的边坡基本都是双面边坡。研究表明[13],双面边坡的地震动响应较单面边坡更为强烈,危害也更为严重。通过数值模拟手段,研究地震对双面边坡稳定性的影响还很少,有必要进一步研究。

本文以数值模拟为计算方法,建立了两侧坡比不同的高陡泥岩双面边坡,通过分析地震时各监测点的位移和速度变化趋势,对坡体的稳定进行判定,并同时分析地震前后坡体内部塑性区范围,最后结合强度折减法[14]计算的滑裂面定量确定地震前后边坡的安全系数。

1 双面边坡模型构建

计算模型选用西南地区典型的高陡泥岩双面边坡。为了排除变坡因素的影响,左侧边坡按坡比1∶0.5 进行建模；右侧边坡坡度稍缓,坡比为1∶1。山体顶部平台宽18 m,边坡总高度100 m。地表以下是2层厚20 m、长100 m的强风化砂岩和弱风化砂岩。边坡模型见图1。各类岩体的主要物理力学参数见表1。

为研究山体两侧不同坡度边坡在地震过程中的位移和速度变化,实时对地震动力计算过程中坡体的位移和速度进行监测,在两侧坡体两侧表面选取了6个监测点。其中,左侧为A、B、C等3个点；右侧为D、E、F等3个点,B、E点距离水平地表垂直高度50 m。

表1 岩体物理力学参数

本文计算选用的地震波最大加速度为100 cm/s2,相应的最大地震加速度a=0.102g,基本烈度相当于Ⅶ度,并按标准比例进行缩放,地震波总持续时间为9.475 s。地震波加速度时程见图2。

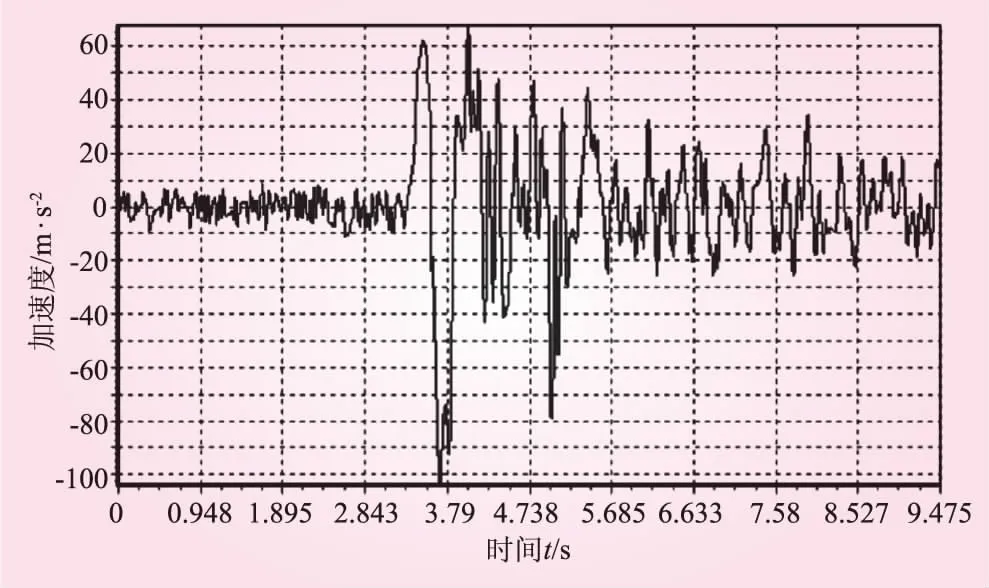
图2 地震波加速度时程

采用二维有限元程序PLAXIS-2D作为数值模拟的计算方法。计算过程中,双面边坡岩体及地层砂岩材料均为弹塑性材料,采用Mohr-Coulomb屈服准则,边界条件采用标准的地震粘滞吸收边界,阻尼采用局部阻尼。地震动力计算过程中,将地震波参数制作为美国地质调查局(USGS)强震记录的标准格式*.smc,并导入程序中进行动力计算。

2 地震时双面边坡稳定性分析

2.1 位移

边坡处于稳定状态时,监测点的位移时程曲线时段末的位移趋势是收敛的,具体表现在位移时程曲线上的位移最终不再随时间变化。当边坡即将进入失稳状态时,时段末监测点的位移趋势是发散的,表现在位移时程曲线上的位移随时间不断增加。规定x向位移水平向右为正,向左为负；y向位移垂直向上为正,向下为负。

图3为双面边坡左、右两侧监测点的x向位移时程曲线。图4为双面边坡左、右两侧监测点的y向位移时程曲线。各图显示出所有监测点在t=9.475 s后的位移均不在发生变化,说明位移时程曲线时段末的位移趋势是收敛的,由此可以判定地震后的边坡是稳定的。进一步分析图3、4可知,位于坡顶的C、D点的x向水平位移最大,最大负向水平位移可达8 cm,其次是位于边坡中部的B、E点,主要位移方向均朝向边坡两侧的临空面；而位于坡脚的A、F点的x向水平位移最小，A、F点的y向位移也很小,可以不予考虑；而B、C点y向位移基本为负值,最大为2.7 cm,说明地震过程中左侧边坡中上部位有发生滑动的趋势；位于右侧边坡中部的E点发生最大1 cm左右的y向正向位移,但震后为负；而坡顶的D点位移基本表现为负值,说明地震时左侧边坡的下滑趋势将带动右侧边坡上部岩体共同发生连锁反应,但下部不受影响。

图3 监测点x向位移时程

图4 监测点y向位移时程

2.2 速度

边坡处于稳定状态时,各个监测点的速度时程曲线时段末的速度趋于0；边坡处于失稳状态时,时段末关键点的速度保持不变或继续增大；规定速度方向与位移方向正负值一致。根据这一原则,绘制了左、右侧边坡各监测点x、y向的速度时程,见图5、6。各图显示所有监测点在时程曲线时段末的速度均趋于0,说明震后的双面边坡是稳定的,与通过位移判定的双面边坡处于稳定状态的结论相同。进一步分析图5、6可知,位于坡顶的C、D点的水平速度最大,地震时最大水平速度可达0.5 m/s；其次是位于边坡中部的B、E点,地震时最大水平速度为0.25 m/s；而位于坡脚的A、F点的速度很小,可以忽略不计；位于左侧边坡的B、C点的y向速度较大,最大为0.20 m/s,在4s左右最为明显,后期有逐渐减小的趋势；位于右侧边坡中部的E点的速度大于顶部的D点,最大速度为0.13 m/s,这与左侧边坡不同。

图5 监测点x向速度时程

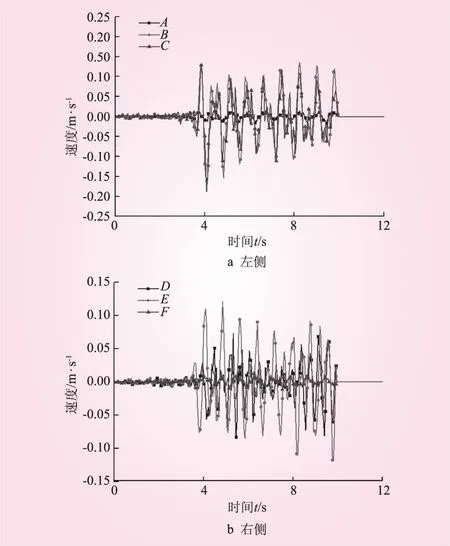
图6 监测点y向速度时程

对地震时双面边坡两侧表面各个监测点的x、y向位移和速度分析发现,双面边坡模型在最大地震加速度0.102g的作用下基本稳定,不会发生滑坡,但左侧1∶0.5的较陡边坡有滑动的趋势。

2.3 边坡安全系数

对双面边坡位移和速度的分析表明边坡仍稳定,但未定量确定地震后边坡的稳定程度。因此,进一步采用有限元软件PLAXIS-2D,采用强度折减法定量计算了地震前后边坡的安全系数。

图7为地震发生前天然状态下边坡计算结果(安全系数Fs=1.32)。从图7可知,仅在左侧较陡边坡中下部局部存在塑性区,双面边坡稳定性良好。

图7 天然状态下边坡计算(Fs=1.32)

图8为地震后边坡计算结果。从图8可知,地震后左侧边坡塑性点大量分布,从左侧坡脚几乎贯通到右侧边坡中上部,有明显的滑动趋势,并导致右侧边坡中上部(距地面80 m)受拉明显,出现局部拉断破坏,这与上文分析所得结论相同。地震后,边坡的安全系数仅为1.08,远小于天然状态下的1.32。但地震前后的滑裂面基本相同。

图8 地震后边坡计算(Fs=1.08)

3 结 语

本文采用二维有限元程序PLAXIS-2D作为地震数值模拟的动力计算方法,系统地研究了强震作用下双面坡的地震响应规律,并结合强度折减法计算的滑裂面定量计算了地震前后边坡的安全系数,得到以下结论：

(1)位移时程和速度时程曲线表明,地震后,双面边坡仍处于稳定状态,但左侧较陡边坡有明显的滑动趋势,并带动右侧较缓边坡上部岩体发生变形,但下部不受影响。

(2)地震后,左侧较陡边坡内塑性点分布范围明显扩大,并贯穿到右侧较缓边坡80 m高处。向左侧的滑动趋势可造成右侧边坡局部岩体拉断破坏。

(3)地震后边坡安全系数仅为1.08,稳定性较差,远小于地震前的1.32。地震前后边坡滑裂面基本相同。

[1]许强, 黄润秋. 5.12汶川大地震诱发大型崩滑灾害动力特征初探[J]. 工程地质学报, 2008, 16(6)： 721- 729．

[2]LESHCHINSKY D, SAN K C. Pseudo-static seismic stability of slopes: design charts[J]. Journal of Geotechnical Engineering, 1994, 120(9)： 1514- 1532．

[3]BAKER R, GARBER M. Theoretical analysis of the stability of slopes[J]. Geotechnique, 1978, 28(4)： 395- 411．

[4]LING H I, CHENG A H D. Rock sliding induced by seismic force[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(6)： 1021- 1029．

[5]AUSILIO E, CONTE E, DENTE G. Seismic stability of reinforced slopes[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(3)： 159- 172．

[6]李海波, 肖克强, 刘亚群. 地震荷载作用下顺层岩质边坡安全系数分析[J]. 岩石力学与工程学报, 2007, 26(12)： 2385- 2394．

[7]肖锐铧, 许强, 冯文凯, 等. 强震条件下双面坡变形破坏机理的振动台物理模拟试验研究[J]. 工程地质学报, 2010, 18(6)： 837- 843．

[8]杨长卫, 张建经, 刘飞成. 双面岩质高陡边坡加速度高程放大效应的时频分析方法[J]. 岩石力学与工程学报, 2014, 33(S2)： 3699- 3706．

[9]邱俊, 任光明, 吴龙科, 等. 金沙江某水电站左坝肩岩体双面倾倒形成机制[J]. 山地学报, 2016, 34(1)： 77- 83．

[10]李兴旺. 频发微震作用下顺层岩质边坡的稳定性研究[D]. 重庆： 重庆大学, 2015．

[11]王东. 地震作用下顺层岩质边坡变形破坏机制研究[D]. 武汉： 华中科技大学, 2015．

[12]SHOU K J, WANG C F. Analysis of the Chiufengershan landslide triggered by the 1999 Chi-Chi earthquake in Taiwan[J]. Engineering Geology, 2003, 68(3)： 237- 250．

[13]YANG C W, ZHANG J J. A prediction model for horizontal run-out distance of landslides triggered by Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration, 2013, 12(2)： 1- 8．

[14]赵川, 付成华, 欧阳朝军, 等. 水位下降对某悬索桥桥基边坡稳定性影响分析[J]. 灾害学, 2016, 31(4)： 134- 138．

(责任编辑杨 健)

ResearchonNumericalSimulationofDouble-sidedSlopeStabilityunderEarthquakeCondition

LIU Sijie, LIU Mingwei

(School of River & Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

The two-dimensional finite element program PLAXIS-2D is used to systematically study the seismic response law of double-sided slope under earthquake conditions and the slip surface and safety coefficient of slope before and after earthquake are calculated. The results show that: (a) the double-sided slope is still in steady state after earthquake; (b) the steep side slope (left slope) has obvious sliding trend and drives the upper rock mass of slowly side slope (right slope) to appear shear sliding; (c) the plastic range of steep side slope expands significantly and run through to right slope at the position of 4/5 slope height, which causing the tensile failure of local rock in right slope; (d) after earthquake, the safety coefficient of slope is only 1.08, which is far less than the value of 1.32 before earthquake; and (e) however, the sliding surfaces are same after and before earthquake．

earthquake load; double-sided slope; stability analysis; PLAXIS-2D

2017- 01- 17

国家自然科学基金项目(51479014)；四川省交通运输科技项目(2015B1-3)

刘思杰(1994—),男,四川成都人,硕士研究生,主要从事岩质边坡稳定性研究．

TU457

：A

：0559- 9342(2017)06- 0028- 04