水文模型参数综合敏感性系数分析
王权威,唐 莉
(太原理工大学水利科学与工程学院,山西太原030024)
水文模型参数综合敏感性系数分析
王权威,唐 莉
(太原理工大学水利科学与工程学院,山西太原030024)
水文模拟中的双超产流模型需要一系列具有空间分布特征的参数对流域产流过程进行模拟。以榆社水文站10场次洪水为研究对象,以双超模型参数经验初值作为基值,采用扰动分析法对参数的敏感性进行分析优化。通过参数调节与模拟计算,得到各参数对洪水的敏感性系数,借助变异系数法算出模型参数的综合敏感性系数。研究表明,模型参数对应不同的水文要素,其敏感性系数与相关性会有所改变,各水文要素下参数综合敏感性系数大小排序为Sr>b>Ks>α0>σ≈c。
敏感性系数;参数分析;扰动分析法;变异系数法;双超模型
流域水文过程受气象条件和流域下垫面的共同作用,在时空尺度上发生着巨大的变化[1]。双超产流模型要求输入的参数较多,并且由于参数在获取过程所产生的误差以及评估的困难,使得确立模型参数值的工作量很大,模型的运行效率和模拟精度不高[2-3];本文以适用于半干旱半湿润地区的双超产流模型为研究对象[4],通过对模型参数进行敏感性分析,识别模型输出响应的重要影响参数,为参数率定提供条件,进而减少模型参数率定过程中的盲目性,提高模型运行的可靠性与预报精度[5]。
1 研究区概况与资料来源
榆社水文站位于榆社县箕城镇,控制流域面积702 km2,属海河流域南运河水系的浊漳河北源的上游端。流域内多年平均降雨555.2 mm,实际发生最大降雨量724 mm(2003年),最小降雨量259.1 mm(1965年),汛期占全年降雨量的65%,多年平均蒸发量1 200 mm。
研究资料皆来自榆社水文站与控制流域内10处雨量站连续记录的降雨量摘录表、洪水摘录表、日蒸发资料。
2 模型介绍
2.1 模型建立
双超模型所模拟的产流机理是面对单元的而非全流域的。其基本概念是将径流成分(即水源)分为超渗径流和超持径流两部分。为反映下垫面和气象等因素的空间变化,双超模型需对流域进行离散化处理,每个离散单元有对应的模型参数。双超产流模型要求输入的参数较多;而且由于参数在获取过程中所产生的误差以及评估的困难,使得确立模型参数值的工作量很大,模型的运行效率和模拟精度不高[1]。本文对模型参数进行了空间等比例缩放,引入了比例因子简化参数调整方式。
利用数字高程模型DEM,由空间分析绘出流域、流域河网与子流域边界,提取各流域水文要素。流域离散化要在其他数据的空间分辨率允许条件下尽可能地细化,以便于区分空间要素分异性并提高处理的精度[6]。各单元有关地形参数由数字流域自动提取,在各单元上独立计算产流量与蒸散发量。
2.2 模型参数及取值范围
双超模型主要有9个参数,本文研究参数具体说明如下:
(1)Sr为充分风干土壤的宏观吸收率,是指土壤对水分的最大吸收能力随土质的不同而不同。其取值范围一般为16~43。
(2)Ks为饱和土壤的宏观导水率,是指土壤水分饱和时的渗透能力随土质不同而异一般在土壤疏松、植被覆盖情况好的地区该值较大;在植被覆盖情况差的地区较小。其取值范围一般为1.1~4.1。
(3)b为反映流域归一化曲线线型的参数b。其值越大模拟的地表径流越大,取值范围一般为1~6。
(4)σ为侧排系数每一土层对应一个侧排系数σi。σi值越大则超持径流越大,取值范围一般为0~1。
(5)C为土壤孔径级配参数,反映土壤颗粒的级配情况。其视不同地区的土壤级配好坏而异,无量纲。其取值范围一般为3~6。
(6)α0为临界雨强因子,反映流域产流临界雨强的参数。其取值范围一般为0~0.5之间。
3 参数敏感性分析
3.1 敏感性分析理论依据
本文采用局部分析法对参数空间中的一点进行敏感性分析[7]。将模型参数Sr、Ks、C、b上下变动10%,α0、σ上下变动0.01,计算输出结果的变化情况。本文使用相对敏感性值将参数敏感性归一化,计算敏感性指数I,进行参数之间敏感性的对比
I=(ΔO/ΔFi)·(Fi/O)
(1)
式中,O为模型模拟输出结果;Fi为影响O的因子(参数);ΔO为模型模拟输出结果的改变量;ΔFi为表示影响O的因子(参数)的改变量。
根据I,可将敏感性进行分类(分类标准见表1)。

表1 参数敏感性分类
3.2 参数敏感性分析
应用式(1)将计算得到的10场洪水的洪量和洪峰进行对比(见表2)。

表2 1966年洪水参数敏感性分析
表2中正负号表示参数变化与洪峰及洪量的相关性,正号为正相关,负号则为负相关。对所选10场次洪水分别进行参数敏感性计算,求得参数敏感性均值(见表3)。
表3中参数Sr、Ks、b对洪量的敏感性大于对洪峰的敏感性,且敏感性差值大小排序为Sr>Ks=b。
4 参数综合敏感性系数的确定
4.1 变异系数法
从前述分析可知,模型参数敏感性大小是相对的,对应不同水文要素时,其模拟结果是有所不同的。本文采用变异系数法计算综合敏感性系数。
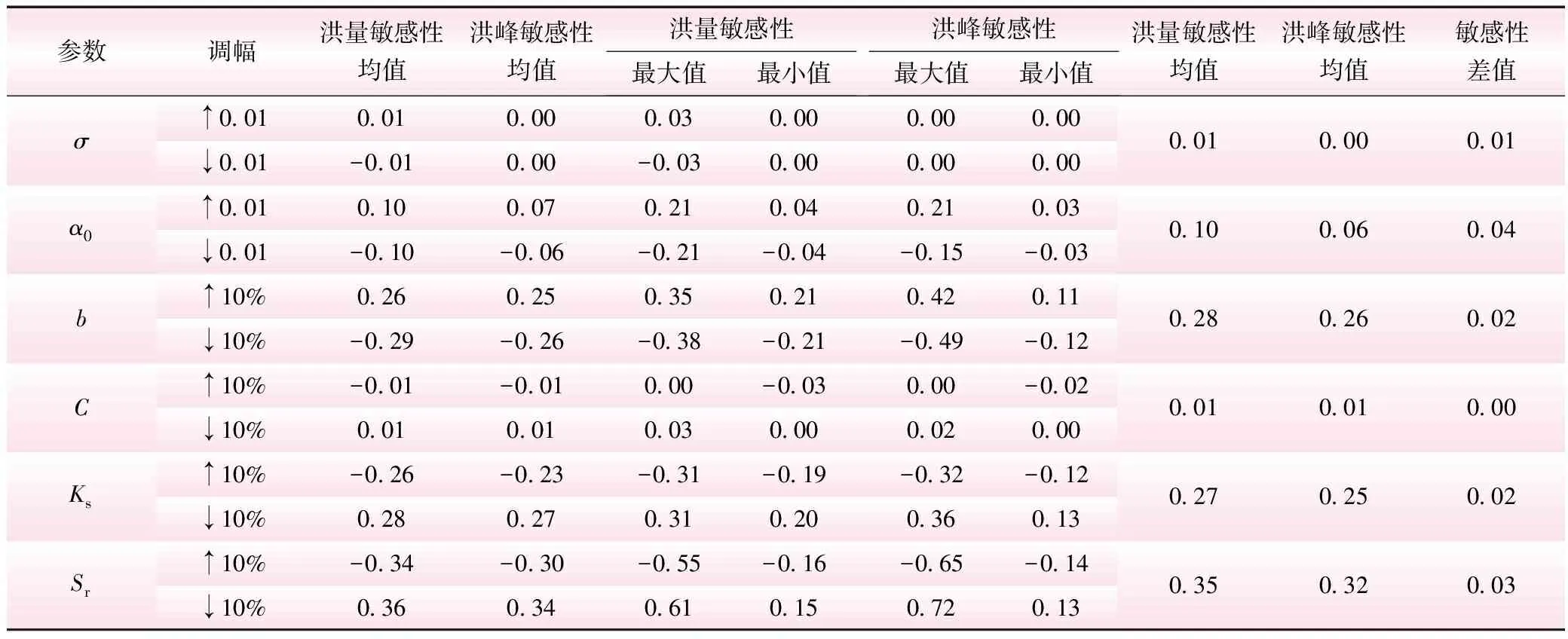
表3 参数敏感性分析成果
设有n个评价指标,每个评价指标中有m个指标数值,则各项指标的标准差

(2)

各项指标的变异系数
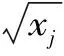
(3)
式中,vj为第j项评价指标的变异系数。各项指标在所有评价指标中所占的权重
(4)
式中,wij为第j项评价指标在所有指标中所占的权重。
4.2 成果对比
应用变异系数法结合表3可得模型参数综合敏感性系数(见表4)。

表4 模型参数综合敏感性系数
由表4可得:模型参数综合敏感性大小排序为Sr>b>Ks>α0>σ≈c;参数Sr、b、Ks为敏感性参数;参数α0为一般敏感参数;C为不敏感参数。
前人曾对双超模型参数采用传统扰动分析法对模型参数进行了敏感性分类[6],但未对模型参数敏感性系数进行定量计算。本文通过定向的改变参数大小,在定量计算模型参数敏感性的基础上,得到了其与目标函数的相关性;再结合变异系数法对目标函数进行赋权,定性定量地对参数敏感性进行了客观全面的分析,成果更加完善与可靠。
5 结 论
(1)参数Sr、Ks、b敏感性等级为Ⅲ级,属于敏感性参数,参数α0敏感性等级为II级,属于一般敏感参数,参数C、σ敏感性等级为I级,属于不敏感参数;各水文要素下参数综合敏感性系数大小排序为Sr>b>Ks>α0>σ≈C。
(2)参数Sr、Ks、b对洪量的敏感性大于对洪峰的敏感性,且敏感性差值大小排序为Sr>Ks=b。
(3)参数σ、α0、b与洪峰洪量正相关,随着σ、α0、b值增大,洪峰与洪量值均增大,参数Sr、Ks、C与洪峰洪量负相关,随着Sr、Ks、C值增大,洪峰与洪量值均减小。
在参数率定过程中可根据计算结果结合参数敏感性差异选取适宜参数进行调节,可有效减少模型的调参工作量。本文研究内容对洪水预报调参与深入了解双超模型产流机理具有实际意义。
[1]孟碟. 水文模型参数的灵敏度分析[J]. 水利水电技术, 2012(02): 5- 8.
[2]廖卫红, 雷晓辉, 张峰, 等. 分布式水文模型EasyDHM在西江流域的应用[J]. 水利水电技术, 2013(12): 8- 11.
[3]SONG X M, ZHAN C S, KONG F Z, et al. Advances in the study of uncertainty analysis of large-scale hydrological modeling system[J]. Journal of Geographical Science, 2011, 21(5): 801- 819.
[4]CIBIN R, SUDHEER K P, CHAUBEY I. Sensitivity and identifiability of stream flow generation parameters of the SWAT model[J]. Hydrological Processes, 2010, 24(9): 1133- 1148.[5]徐会军, 张鹏程, 董爱红. 多参数敏感度方法在分布式水文模型的应用[J]. 水利科技, 2013(3): 4- 8.
[6]晋华. 双超式产流模型的理论及应用研究[D]. 北京: 中国地质大学(北京), 2006.
[7]孙飞飞, 许钦, 任立良, 等. 水文模型参数敏感性分析概述[J]. 中国农村水利水电, 2014(3): 92- 95.
(责任编辑陈 萍)
ParametersSensitivityAnalysisofHydrologicModel
WANG Quanwei, TANG Li
(College of Water Resources Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China)
A series of parameters which have spatial distribution characteristics is required in double-excess runoff generation model to simulate the process of watershed runoff. Taking ten floods in Yushe Hydrological Station as research object, the sensitivity of parameters is analyzed and optimized by using perturbation analysis method, in which, the empirical values of parameters of double-excess runoff generation model are used as base values. The sensitivity coefficients of various parameters on flood are obtained through parameter adjustment and simulation scenarios, and the comprehensive sensitivity coefficient of model parameters is also calculated by using variation coefficient method. The analysis results show that the sensitivity coefficients and correlations of model parameters will change when it is in different hydrological elements, and the magnitude of comprehensive sensitivity coefficient of parameters under different hydrological elements has a order ofSr>b>Ks>α0>σ≈c.
sensitivity coefficient; parameter analysis; perturbation analysis method; variation coefficient method; double-excess runoff generation model
2016- 06- 27
国家自然科学基金资助项目(51509176)
王权威(1992—),男,山西吕梁人,硕士研究生,研究方向为水文及水资源;唐莉(通讯作者).
TV877
:A
:0559- 9342(2017)06- 0016- 03

