基于广义变分原理和锯齿理论的高精度层合梁模型

贺 丹，杨万里

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136)

基于广义变分原理和锯齿理论的高精度层合梁模型

贺 丹，杨万里

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136)

基于广义变分原理和精化的zigzag理论建立了高精度的层合梁弯曲和自由振动模型。为准确预测层合梁的力学行为做出两个预处理：首先采用线性zigzag函数[1]使面内位移在梁高度方向(z方向)上呈锯齿分布；然后通过弹性平衡方程构造了预先满足层间连续和自由表面条件的层间横向剪力，因此不需要剪切修正因子。另外，基于Reissner混合变分原理推导了该梁模型的控制方程和边界条件，并以正交铺设的两端简支层合梁为例，分析了静弯曲和自由振动行为。算例结果表明，该模型能够准确地预测位移、应力和自振频率，验证了本文方法的精度和可靠性。

Reissner混合变分原理；层合梁；层间应力；zigzag函数

0 引言

复合材料层合板/梁结构由于轻质、耐腐蚀及可设计性等优点广泛应用于土木工程、航空航天等领域。在实际应用中，层合板/梁结构的主要破坏形式之一是层间的横向剪力引起的分层破坏，现有软件尚未考虑层间连续条件而无法准确地计算层间应力。因此对层间横向剪力进行准确的计算非常必要[1-8]。

为准确预测层合结构的层间应力，位移函数沿高度方向必须预先满足层间连续条件[9]，而位移的1阶导数不连续，即呈锯齿分布。为模拟该条件，分层理论[3]通过对每个单层构造运动学方程来满足；整体局部理论[10]通过定义高阶局部函数来满足；zigzag理论[11]通过在面内位移场添加线性局部函数来满足。基于分层理论，Plagianakos等[3]精确地预测了层合结构的面内位移分布和层间应力分布。基于整体局部理论，Wu等[10]采用有限元法由求得的应变精确计算了层间横向剪力和面内应力，并采用平衡方程后处理方法准确计算了层间法向应力。近来，Iurlaro等[11]基于精化的zigzag理论，通过Reissner混合变分原理对弹性平衡方程进行预处理构造了满足上下表面条件和层间连续性条件的剪应力，并求解了板的自振频率；文献结果表明[11-12]，该模型在处理复合材料层合结构问题时具有非常高的精度。与分层理论和整体局部理论相比，精化的zigzag理论中对单层位移的定义更为简便，计算效率更高，且未知变量的个数独立于层合结构的层数，非常适合工程应用。另外，通过Reissner混合变分原理对弹性平衡方程进行预处理所得的结果比其他方法所得的结果更加精确。

因此，本文基于精化的zigzag理论和广义变分原理建立了预先满足层间连续条件和自由表面条件的层合梁弯曲和自由振动模型。另外，基于Reissner混合变分原理推导了该模型的平衡方程和边界条件。文中以正交铺设的两端简支梁模型为例，分析了不同铺设方式下弯曲变形和自由振动，并与相关文献进行对比检验本文方法的精度。

1 层合梁模型

1.1 位移场

基于精化zigzag理论[1]的梁模型如图1所示，其位移场以1阶Timoshenko梁函数为基础函数，并分层添加线性zigzag函数模拟了面内位移在高度z方向上呈锯齿分布，具体表达式为：

uk=u0(x,t)+zθ(x,t)+φk(z)ψ(x,t)

w=w(x,t)

(1)

其中，u0为中面的平动位移，w为挠度，θ为截面转角，k表示第k层，φk(z)为第k层的线性zigzag函数，ψ(x)为zigzag幅值函数。图中，zk=zk-1+2hk，2hk为第k层的高度，N表示层数。另外，z0=-h，zN=h，分别表示梁的上下表面，z∈(-h，h)。pt和pb分别表示上下表面的外载荷。

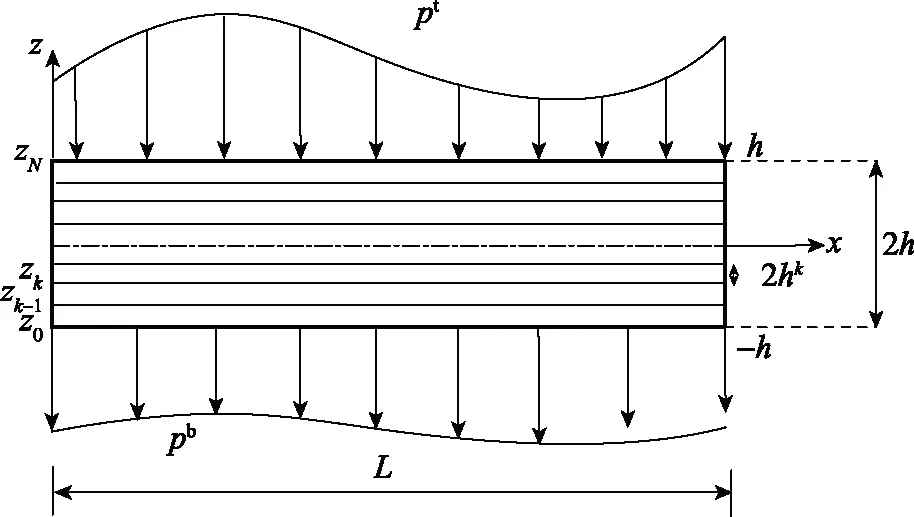
图1 层合梁承载示意图Fig.1 Schematic figure of a laminated composite beam subjected to transverse loads

分层表示的线性zigzag函数[1]可写成：

(2)

(3)

其中，uk(k=1,2,…,N)为层间轴向位移[1]。

1.2 层合梁的本构方程

经坐标变换之后，第k层的应力-应变关系在结构坐标系(x,y,z)下可以写为：

σk=Qkε

(4)

其中,

ε=[εxγxz]T

(5)

Qk=TkTCkTk

(6)

其中,T为坐标变换矩阵，C为材料弹性系数矩阵。

梁的刚度矩阵Qk，表述如下：

(7)

2 层间应力连续的前处理

为满足层间应力连续条件，进行如下预处理[11]：

1)忽略体力的第k层平衡方程可写成：

(8)

将式(4)代入式(8)，则式(8)可改写成：

(9)

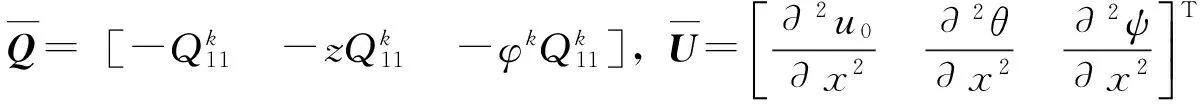
2)式(9)等号左右两端沿z方向积分可得：

(10)

3)将z=h代入式(10)，则

(11)

(12)

4)将式(12)代入式(10)，层间横向剪力可表示为：

(13)

其中，

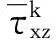
(14)

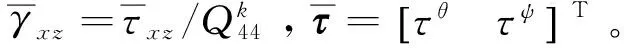
3 平衡方程与边界条件

根据Reissner混合变分原理，放松剪应变和替换剪应力后得到的修正泛函[11-12]的变分可表示为：

(15)

(16)

其中,We为外力功，Wi为惯性力做的功。式(15)表示域内的平衡，式(16)为用Lagrange乘子表示的应变约束条件。

(17)

其中,B=[1 ∂φk/∂z],q=[θ+∂w/∂xψ]T。

将式(17)代入式(13)，层间横向剪力的表达式变为：

(18)

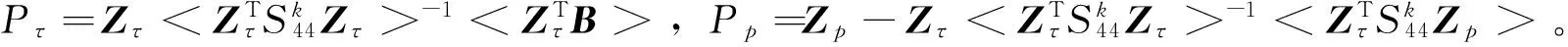
将式(1)和式(18)代入式(15)并分部积分，则式(15)可改写成：

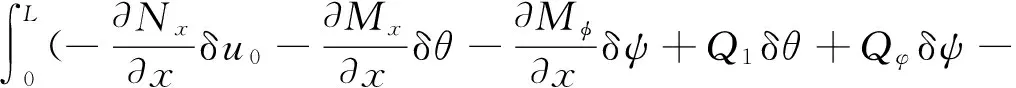
δWe-δWi=0

(19)

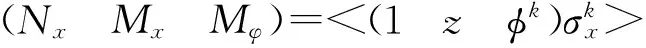
外力功的一阶变分可表示为：

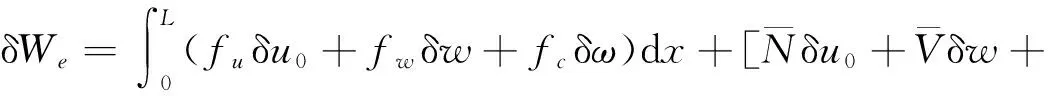
(20)

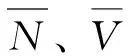
(21)

惯性力所做的功的一阶变分可表示为：

(22)

令

m0=<ρk>,m1=,m2=

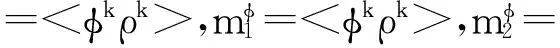
(23)

则惯性力所做的功一阶变分可改写成：

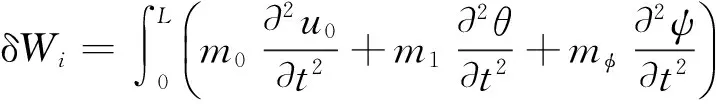
(24)

将式(20)、(21)和(24)代入式(19)可得梁的平衡方程为：

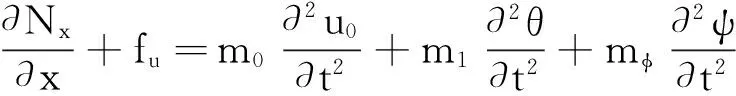
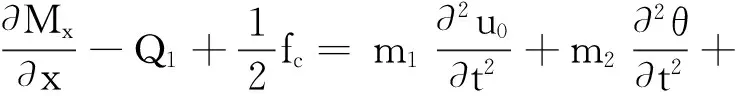
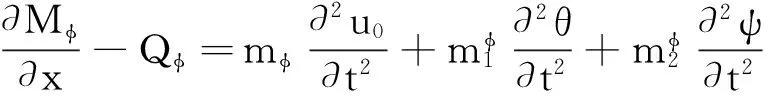
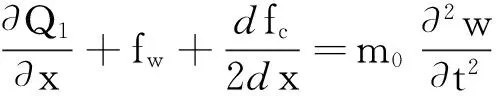
(25)

在x=0和x=L处的边界条件为：

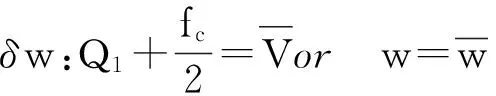
(26)

将本构方程代入式(25)，用位移表示的平衡方程可表示为：

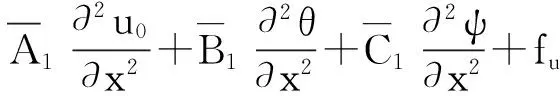
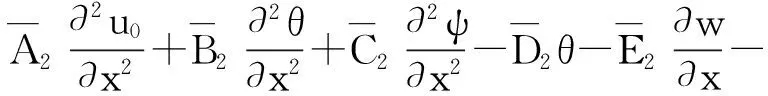
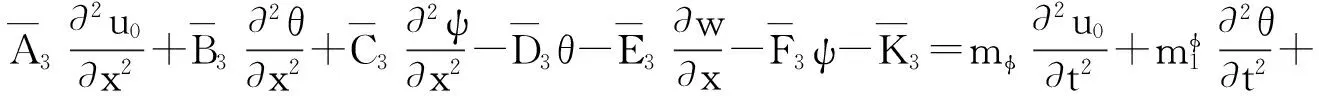
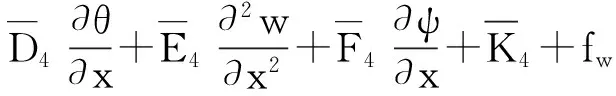
(27)

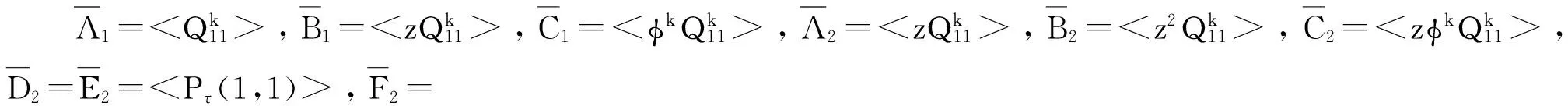
4 算例

以正交铺设的简支层合梁为例，首先对受正弦载荷时的弯曲行为进行分析并检验了本文方法的精度。如图2所示，简支梁仅承受z向圆柱弯曲载荷fw=q0sin(πx/L)，且各单层的高度和材料属性均相同。另外，进一步分析了该模型的自由振动行为。

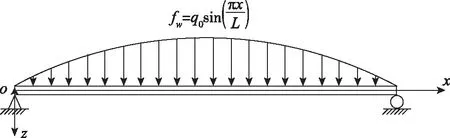
图2 简支梁示意图Fig.2 Schematic figure of a simply supported beam

简支梁的边界条件为：

(28)

(29)

4.1 弯曲分析

对于弯曲分析，由于没有惯性力，因此令Wi=0。另外，满足全部边界条件的位移函数可设为：

(30)

4.1.1 位移与正应力

4.1.2 层间横向剪切应力

(a)0°/90°

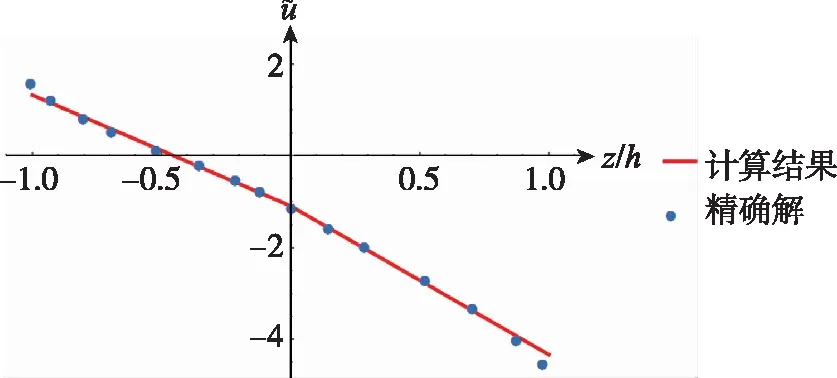
(b)0°/90°/0°图3 x=0处的轴向位移Fig.3 The axial displacement at x=0

(a)0°/90°

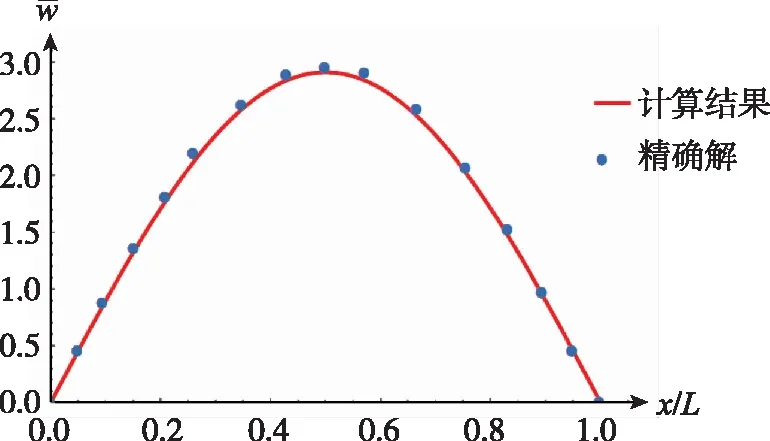
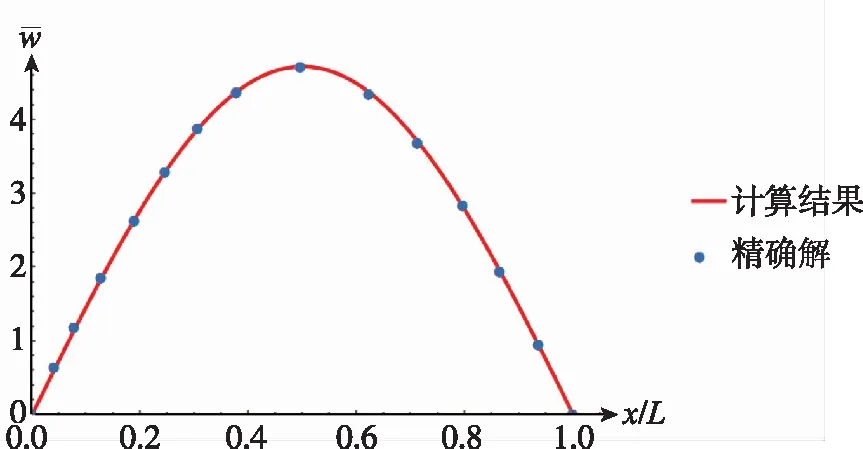
(b)0°/90°/0°图4 梁中面挠度Fig.4 Center deflection of the beam

(a)0°/90°

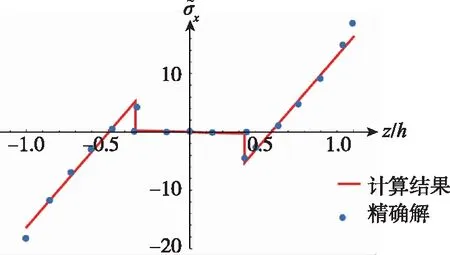
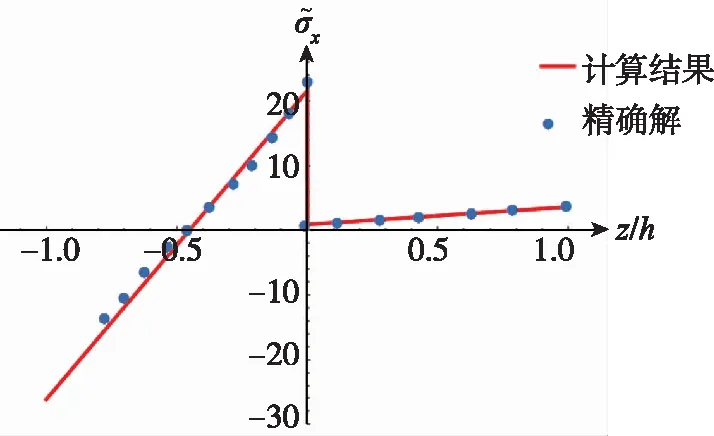
(b)0°/90°/0°图5 x=L/2处的正应力Fig.5 The normal stress at the mid-span at x=L/2

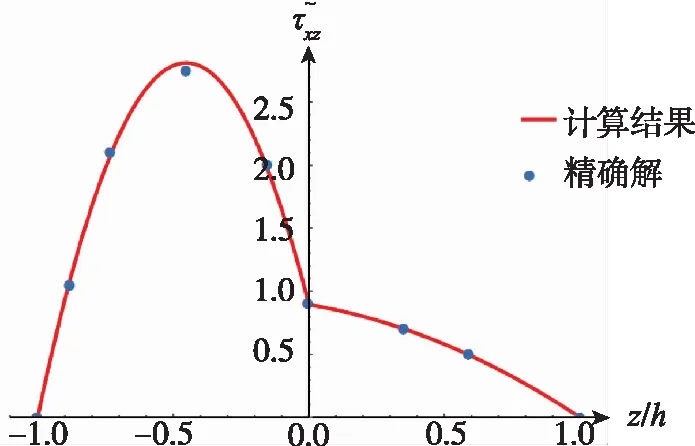
(a)0°/90°

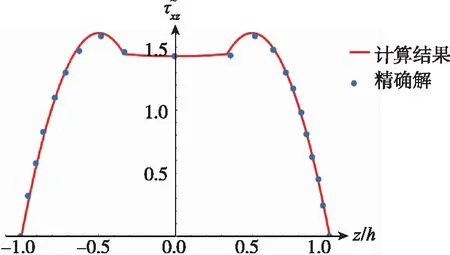
(b)0°/90°/0°

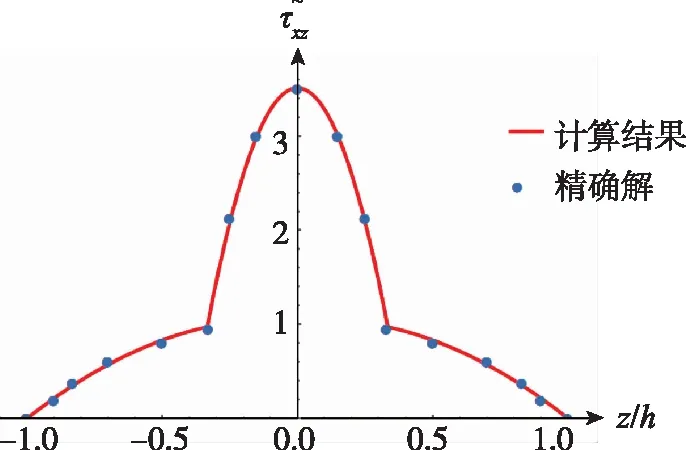
(c)90°/0°/90°

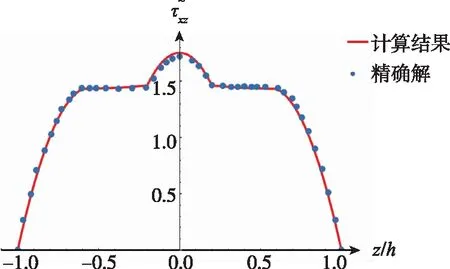
(d)0°/90°/0°/90°/0°图6 x=0处梁的剪应力Fig.6 The transverse shear stress of the beam at x=0

4.2 自由振动分析

本节分析了正交铺设简支层合梁的自由振动，并给出了不同铺设方式下的自振频率。对于自由振动分析，满足全部边界条件的位移函数可设为：

(31)

其中,ωn为自振频率，i2=-1。

将式(31)代入式(27)，则层合梁的控制方程可改写成：

Ku=ω2Mu

(32)

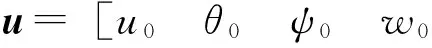
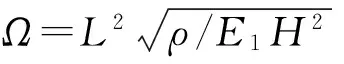
由表1可知：0°/90°/90°/0°铺设时，本文结果与文献解[14]吻合。但文献[14]中采用了1阶剪切变形理论，不能满足层间连续条件和上下自由表面条件，因此，采用了剪切修正因子进行了修正。然而剪切修正因子在不同材料中取不同的值[15]，不具有普适性。本文的自由振动模型预先满足层间连续条件和自由表面条件，不需要采用剪切修正因子，因此更适合工程应用。

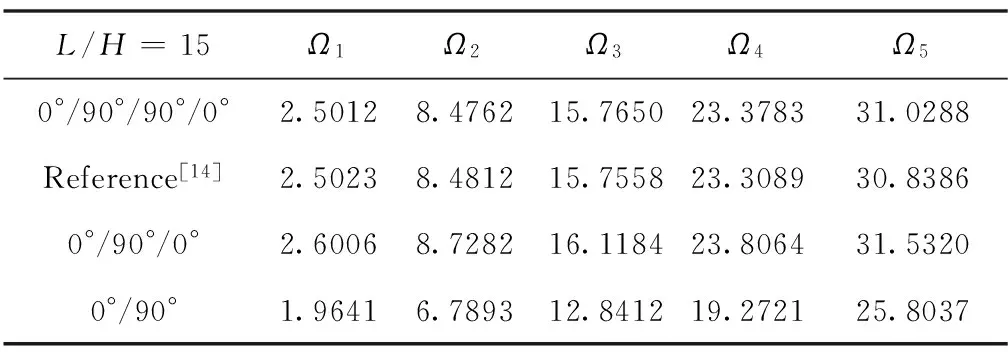
表1 不同铺设方式下层合梁的自振频率

5 结论

与采用1阶理论的梁模型相比，本文基于zigzag理论和Reissner混合变分原理建立的层合梁弯曲和自由振动模型预先满足了层间连续条件和自由表面条件，不需要剪切修正因子。另外，该模型梁高方向的位移函数呈锯齿分布，能够准确地预测层间应力，且未知变量的个数不随层数的增加而增加。研究结果表明，本文模型不仅可以准确地预测梁的位移、应力和自振频率，而且不牺牲计算效率。因此，该梁模型在航空航天等领域有着广泛的应用前景。

[1] Tessler A, Sciuva M D, Gherlone M. A consistent refinement of first-order shear deformation theory for laminated composite and sandwich plates using improved zigzag kinematics[J]. Journal of Mechanics of Materials & Structures, 2010, 5(2): 341-367.

[2] Xiaohui R, Wanji C, Zhen W. A C0-type zigzag theory and finite element for laminated composite and sandwich plates with general configurations[J]. Archive of Applied Mechanics, 2011, 82(3): 391-406.

[3] Plagianakos T S, Saravanos D A. Higher-order layerwise laminate theory for the prediction of interlaminar shear stresses in thick composite and sandwich composite plates[J]. Composite Structures, 2009, 87(1): 23-35.

[4] Rao M K, Desai Y M. Analytical solutions for vibrations of laminated and sandwich plates using mixed theory[J]. Composite Structures, 2004, 63(3-4): 361-373.

[5] Kant T, Swaminathan K. Analytical solutions for the static analysis of laminated composite and sandwich plates based on a higher order refined theory[J]. Composite Structures, 2002, 56(4): 329-344.

[6] Matsunaga H. Assessment of a global higher-order deformation theory for laminated composite and sandwich plates[J]. Composite Structures, 2002, 56(3): 279-291.

[7] Kant T, Swaminathan K. Analytical solutions for free vibration of laminated composite and sandwich plates based on a higher-order refined theory[J]. Composite Structures, 2001, 53(1): 73-85.

[8] Gaudenzi P, Barboni R, Mannini A. A finite element evaluation of single-layer and multi-layer theories for the analysis of laminated plates[J].Composite Structures, 1995, 30(4): 427-440.

[9] Biscani F, Giunta G, Belouettar S, et al. Variable kinematic plate elements coupled via Arlequin method[J]. International Journal for Numerical Methods in Engineering, 2012, 91(12): 1264-1290.

[10] Wu Z, Chen R, Chen W. Refined laminated composite plate element based on global-local higher-order shear deformation theory[J].Composite Structures, 2005, 70(2): 135-152.

[11] Iurlaro L, Gherlone M, Di Sciuva M, et al. Refined Zigzag Theory for laminated composite and sandwich plates derived from Reissner’s Mixed Variational Theorem[J]. Composite Structures. 2015, 133: 809-817.

[12] Iurlaro L, Gherlone M, Sciuva M D. The (3,2)-Mixed Refined Zigzag Theory for generally laminated beams: Theoretical development and C0finite element formulation[J]. International Journal of Solids & Structures, 2015, 73: 1-19.

[13] Pagano N J. Exact solutions for composite laminates in cylindrical bending[J]. Journal of Composite Materials, 1969, 3(3): 72-85.

[14] Kidwell C. Free vibration of composite beams including rotary inertia and shear deformation[J]. Composite Structures, 1990, 14(4): 269-279.

[15] Ghugal Y M, Shimpi R P. A review of refined shear deformation theories of isotropic and anisotropic laminated plates[J]. Journal of Reinforced Plastics & Composites, 2002, 21(9): 775-813.

A High-accuracy Composite Laminated Beam Model Based on Generalized Variational Principle and Zigzag Theory

HE Dan, YANG Wan-li

(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation,Shenyang Aerospace University, Shenyang 110136, China)

A high-accuracy bending and free vibration model of composite laminated beam is developed based on generalized variational principle and zigzag theory. To predict the mechanical behaviors accurately, the following two-step processes are implemented in this paper. Firstly, the linear functions are employed to insure that in-plane displacements through the thickness direction (the direction ofzaxis) are of the zigzag form. Secondly, the interlaminar stresses which satisfy a prior continuity conditions at the interface and free conditions at the surface are derived with the aid of the Elasticity equilibrium equations. Therefore, the transverse shear correction factors are not required. Moreover, the Reissner’s Mixed Variational Theorem is employed to derive the governing equations and the boundary conditions. A simply supported cross-ply beam model is taken as an illustrative example, the problem of static bending and free vibration are analytically solved. Illustrative examples indicate that the displacements, stresses and natural frequencies predicted by present model are accurate which demonstrates the correctness and reliability of present formulation.

Reissner’s mixed variational theorem; Composite laminated beam; Interlaminar transverse shear stress；Zigzag functions

2017-02-28；

2017-04-13

国家自然科学基金(11572204)

贺丹(1979-)，男，博士，副教授，研究方向为微纳米力学、结构优化。E-mail：Danhe@sau.edu.cn

V41

A

2096-4080(2017)02-0026-07