运载火箭总体设计多学科优化方法发展及展望
刘竹生, 张博戎
(1.中国运载火箭技术研究院,北京 100076;2.北京宇航系统工程研究所,北京 100076)
运载火箭总体设计多学科优化方法发展及展望
刘竹生1, 张博戎2
(1.中国运载火箭技术研究院,北京 100076;2.北京宇航系统工程研究所,北京 100076)
运载火箭总体设计是一项涵盖多学科的系统工程。在总体设计过程中,需要综合考虑弹道、气动、姿控等多个学科的设计方案及其相互间的耦合关系。多学科优化(MDO)方法通过不同的单级或多级模型对多学科系统进行近似建模,再利用相应数值算法迭代计算,从而逼近全局最优解。系统回顾了多学科优化方法在国内外的发展脉络,择要介绍了应用于总体设计的经典多学科优化模型架构、软件平台和实际算例,探讨了多学科优化方法在我国运载火箭总体设计中的应用价值和发展前景。
多学科优化(MDO);火箭总体设计;火箭构型优化
1 引言
总体设计是运载火箭研制过程中至关重要的、基础性的工作[1],也是一项涵盖多学科的系统工程。在总体设计过程中,需要综合考虑弹道、气动、姿控、动力、结构、载荷、成本分析等多个学科的设计方案及其相互之间的耦合关系,是一个十分复杂的多学科建模和寻优分析过程。多学科优化(Multidisciplinary Optimization,MDO)方法于20世纪80年代末被引入航天航空领域,并于1993年被NASA白皮书正式定义[2]。MDO方法的主要思想是通过对多学科系统进行一定程度的近似建模,利用数值方法求解问题。该方法在近30年来取得了广泛的发展和应用。
1.1 MDO的技术优势
运载火箭的总体设计方案包含有火箭型式、级数、有效载荷、推进剂种类、动力系统、稳定和矢量控制形式、制导和惯性器件、分离系统、结构型式和部位安排、火箭外形、加注方案等[1],是一个典型的多学科问题,部分学科相互之间存在较强的耦合关系(例如弹道与气动)。如图1所示[3],一个成功的运载火箭总体设计方案需要对这个多学科系统进行合理的综合考虑。

图1 运载火箭总体设计示意图Fig.1 Diagram of launch vehicle design process
在传统的运载火箭总体设计中,各个学科和分系统在接到总体提出的方案要求后,便独立展开设计,相互之间的接口参数大多依靠火箭总设计师的经验进行设定。各学科完成分系统方案后,再通过反复协调,调整接口参数,进一步修正总体方案。由于这一过程的组织复杂性,传统的总体设计方法主要存在以下3点问题:1)没有处理或者无法处理某些学科之间的耦合关系;2)难以找到整体最优解;3)设计效率不高[4]。
MDO方法的出现针对以上3点问题做出了有效改进,该方法通过整体的多学科近似建模,较全面地建立了学科间的耦合关系,并从全局优化角度出发,利用数值计算快速逼近最优解。MDO方法的应用可以使得运载火箭总体设计的效率和准确性都有大幅提升。
1.2 MDO的研究和应用现状
MDO方法首先被应用于飞行器结构尺寸优化等复杂性相对较低的问题中,随后,诸如X-33发动
机总体设计、空中客车A3X0系列飞机构型管理、多种可重复使用运载器(RLV)总体设计等都采用了这一方法,并有相应研究成果发表。
国内学者对于MDO方法的研究起步相对较晚。目前已有利用MDO方法对亚轨道重复使用运载器[5]、空射运载火箭[6]、多级固体导弹和运载火箭[7]等总体设计方面的研究,也有特别针对基于MDO的火箭集成设计技术和平台方案的研究[3,8]。国内学者对于MDO方法的研究和应用从数量和质量上都落后于欧美学者[9],且绝大部分研究对象集中在一般飞行器、卫星系统及星座构型、固体火箭和导弹方面。利用MDO方法进行液体运载火箭总体设计的成果极少,没有实例,也没有综述性文章对这一领域问题进行系统性的总结。
纵观国内外学者对MDO方法近30年来的研究和应用,可以看到其在航天航空领域经历了从无到有、从理论到实践、从简单应用到复杂应用的进化历程。
一方面,现今将MDO方法应用于航天航空实际工程设计仍然存在一些难点,特别是在近似建模和算法求解方面[4,10]。近年来不断有新方法尝试更加精确的建模和求解,但截至目前仍没有很好地解决这一问题。因此,MDO方法在航天航空领域依然具有十分广阔的研究空间。
另一方面,国内的MDO方法研究和应用相对落后,且极少将其应用于液体运载火箭总体设计工作,及时对MDO方法在该领域的进展进行分析和总结,并进一步对其展开深入研究,具有很大的必要性和重要意义。
2 MDO问题的近似建模
运用MDO方法解决实际问题时,针对同一个工程问题,通常可以选用多种不同的MDO模型架构对其进行近似建模[4],不同类别的MDO模型架构使用的求解算法和软件平台也具有一定差异性。因此,MDO模型架构的选取既关乎问题求解的准确性,也关乎计算的高效性,如何适当建立模型架构对MDO问题进行处理是十分关键的第一步。
MDO(multidisciplinary optimization)意义等同于MDO(multidisciplinary design optimization)和MDAO(multidisciplinary design and analysis optimization),本文均统称为MDO。
在国内外学者的长期研究下,现今已发展多种MDO近似建模架构,且各有优缺点,见表1。本文主要选取3种经典的、已在航天航空领域中取得广泛认可的架构进行分类介绍。

表1 MDO近似建模架构比较
2.1 多学科可行(MDF)架构
多学科可行(Multidisciplinary Feasible,MDF)架构是MDO领域应用较早的经典单级架构之一。所谓单级架构,即在同一层面考虑所有学科的控制方程及约束条件,而不进行任何层级的划分。MDF的主要思想可以概括为以下步骤[11]:
1)假设一总体多学科设计变量;
2)全部学科按顺序对该变量进行一次优化;
3)迭代上述过程直到设计变量满足设定收敛要求为止。
MDF架构尽管理论上具有多学科优化思想,且总能找到满足各学科一致性约束的更优解,但是缺点也十分明显。即设计变量的搜索空间极大,计算成本也非常高,在每次优化的循环过程中,所有耦合变量必须全部被重新计算一次并返回优化器。这一缺点在复杂系统的多学科优化过程中会十分凸显[4]。
2.2 单学科可行(IDF)架构
单学科可行(Individual Discipline Feasible,IDF)架构是在MDF架构基础之上,更偏重于单学科独立优化的单级方法。其核心思想是通过再引入一个“一致性约束”来降低多学科间耦合变量的差异,从而驱动在各个学科内的迭代解向全局最优解逼近。相比MDF架构,IDF在一定程度上简化了全局计算过程,具有相对较高的实用性。但是当MDO问题各学科之间耦合变量较多的时候,IDF架构的迭代计算过程仍然十分繁琐[4]。
2.3 协同优化(CO)架构
协同优化(Collaborative Optimization,CO)架构是在单级优化架构基础之上发展建立的多级架构。所谓多级优化架构,即将全局多学科优化问题划分为系统层级和子系统层级,其步骤可以概括如下[11]:
1)系统层级向子系统层级分配参数;
2)子系统内部并行独立优化,再将参数返回系统层级;
3)系统层级通过人为设定的多学科耦合约束,优化子系统返回得到的参数,并继续迭代以上两步,直到满足收敛要求为止。
多级优化通过子系统的划分和并行计算,能够在很大程度上减小优化搜索空间,提升计算效率。CO架构正是基于这一思想,由单级IDF架构发展建立的。通过引入系统级的等式约束,多次迭代可以使得耦合变量与设定值差异减小到一个可行的范围内,从而得到系统层级的最优设计方案[7]。根据优化目标和对鲁棒性要求的不同,国内外学者也在CO架构的基础之上发展了CO1、CO2、MCO、ECO等多级架构[4]。
2.4 建模架构发展趋势
对现有应用于航天航空领域的MDO方法架构进行总结,可以发现以下3个特点和趋势:
1)从模型架构发展的角度来看,MDO近似建模经历了由简单向复杂、由单级向多级、由粗略向精细的进化过程;
2)这一领域的新型优化架构层出不穷,更新速度很快。针对不同的优化问题和优化目标,同一种优化架构可以衍生出多种旁支,实际问题和近似模型之间的匹配性是分析建模过程中十分关键的环节之一;
3)虽然近似建模架构是MDO方法的核心环节,但是现阶段可实际应用于工程设计的MDO近似建模手段还是远远迟滞于模型本身的发展,目前暂时还没有被学界一致认可的能适用于火箭总体设计的MDO架构。
2.5 模型求解平台
在完成MDO问题的近似建模后,即可对其进行计算求解。由于多学科问题的复杂性和学科之间的相互独立性,完全独立编程不具有现实可行性。目前国际上已有多款适用于求解多学科优化问题的软件平台,包括iSight、ModelCenter、FIDO、DARWIN、VisualDOC、Optimus、AML、DAKOTA、CSD、Caffe、DOCS等,可为不同模型的求解提供一定便利[3]。其中,iSight和ModelCenter是两种目前国际上应用最为广泛的求解平台。
iSight是由美国Engineous Software公司开发的通用多学科优化平台软件,目前占据国际上主流通用市场。该软件本身并不会对各学科的问题进行计算求解,而是集成了多种优化技术和近似模型,并可以调用ANSYS、ABAQUS、CATIA、FLUENT、NASTRAN等各学科计算软件进行计算,也被称作“软件机器人”。美国洛克希德马丁公司的“德尔塔”系列运载火箭设计运用了这一平台[12]。
ModelCenter是由美国Phoenix Integration公司开发的多学科设计优化软件平台,与STK、MATLAB、NASTRAN、EXCEL等功能软件均有接口设计。ModelCenter的特点是建模方式灵活,可拓展性强[12]。该软件在国防和工业界中占有一定市场。
3 MDO方法实际工程算例
欧洲宇航防务集团公司(EADS)较早将MDO方法应用于新型火箭的设计和研发,并以阿里安5 ES火箭的构型为蓝本,针对其改进方案进行了多学科优化设计[10]。
EADS学者在优化设计过程中,考虑了5种学科模型之间的耦合关系,分别是载荷、推进、弹道、气动、成本。其中弹道计算是建立在精确方程上,而其他4个学科都采用简化的近似模型。整个优化问题共含有约30个参数变量,10个约束条件。其求解是利用遗传算法(Genetic Algorithm)和一个开源的EO优化器。该项工作在假设火箭构型型式不变(仍然采用2枚固体助推+低温芯级+液体推进上面级的结构型式)情况下,针对GTO和LEO轨道,分别以最小起飞质量和最低整箭成本为优化目标,对阿里安5 ES火箭每级构型参数进行了优化[10]。其问题建模过程可以表述为以下形式:
针对给定的载荷要求和目标轨道参数,找到满足约束的优化参数向量。
P=(pa(1),…,pa(na),pc(1),…,pc(nc))
(1)
其中na为架构参数,nc为指令参数。在此基础之上,利用遗传算法对P进行优化,优化的目标函数为起飞质量
(2)
或为整箭成本
(3)
其中α和β是成本模型F中适用于不同类型箭体的计算参数。
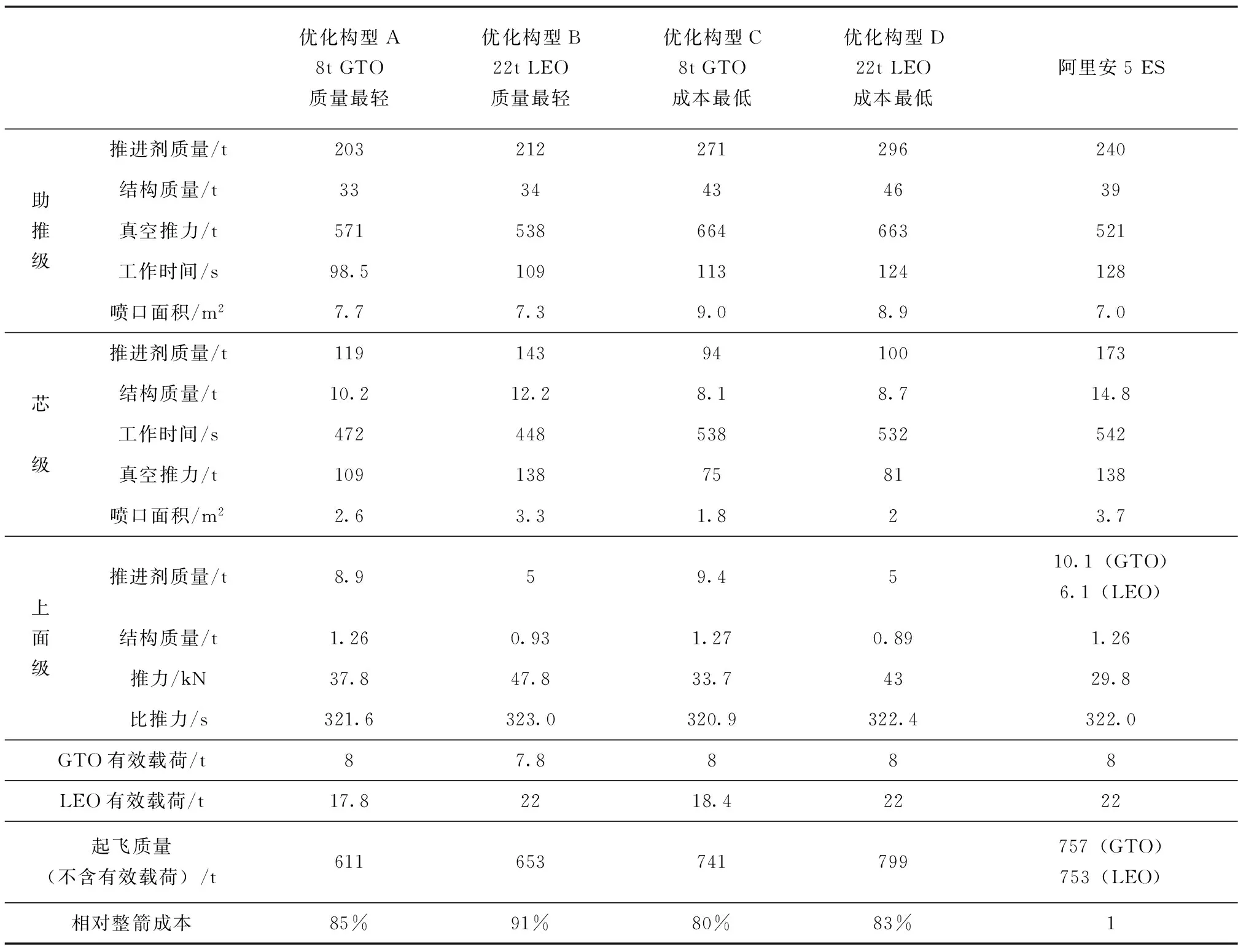
利用这一方法得到的优化结果和示意图见表2和图2[10]。从表2中可以看到,对比阿里安5 ES原始构型和优化构型A(8t GTO,质量最小),在不降低GTO轨道有效载荷的前提下,MDO的设计方案能够降低146t的起飞质量。另外,对比阿里安5 ES原始构型和优化构型D(22t LEO,成本最低)可以看到,在不降低有效载荷能力的前提下,MDO设计方案通过改变助推级、芯级和上面级之间的几何构型尺寸和推进剂配比等参数,能降低17%的成本,这无疑是十分可观的数据。可以预想,如果将MDO方法进一步解除约束条件,即放开关于对火箭级数、推进剂种类等的预定限制,进行全局箭体优化设计,那么将有可能实现更低的整箭成本或起飞质量优化效果。关于这一类问题,EADS正在进行研究。

图2 阿里安5 ES火箭优化构型对比图Fig.2 Optimized configurations of ARIANE 5 ES
优化构型A8tGTO质量最轻优化构型B22tLEO质量最轻优化构型C8tGTO成本最低优化构型D22tLEO成本最低阿里安5ES助推级推进剂质量/t203212271296240结构质量/t3334434639真空推力/t571538664663521工作时间/s98.5109113124128喷口面积/m27.77.39.08.97.0芯级推进剂质量/t11914394100173结构质量/t10.212.28.18.714.8工作时间/s472448538532542真空推力/t1091387581138喷口面积/m22.63.31.823.7上面级推进剂质量/t8.959.4510.1(GTO)6.1(LEO)结构质量/t1.260.931.270.891.26推力/kN37.847.833.74329.8比推力/s321.6323.0320.9322.4322.0GTO有效载荷/t87.8888LEO有效载荷/t17.82218.42222起飞质量(不含有效载荷)/t611653741799757(GTO)753(LEO)相对整箭成本85%91%80%83%1
4 总结与展望
近30年来,随着MDO设计理念在航天航空领域首次提出,这一方法由于适用性广泛,得以迅速发展并取得应用成果。针对MDO方法在运载火箭总体设计中的研究和应用现状,可以概括得到以下两点结论:
1)运载火箭总体设计是一个具有强耦合性的多学科问题,国际上针对适用于这一特定领域的MDO分析建模方法多样,各有优劣。对MDO问题进行合理的简化和约束是解决MDO问题的关键点与难点。
2)相比MDO优化模型和算法的发展,能够应用于运载火箭实际工程设计的MDO方法具有一定迟滞性,国内外学者极少进行过整箭优化算例。MDO方法是否能真正快速应用于工程实践尚有待检验。
在未来我国运载火箭的发展趋势和构想下,“可重复使用”和“先进推进”等重要技术都可能逐步付诸实践[13],此类“革命性”技术在新型运载火箭上的应用,也对总体设计提出了更高、更新的要求[14-15]。针对将MDO方法应用于我国运载火箭总体设计的前景和关键问题,进行展望:
1)进一步发展MDO方法,需要根据现有总体参数计算、弹道、气动、结构、姿控、动力、载荷等学科的模型,建立合理的运载火箭MDO模型,明确学科间的约束和优化目标,利用已有成熟的算法和软件平台进行求解,找出关键节点和影响参数。
2)进一步在实际层面提升MDO方法的应用能力,可以结合现有运载火箭模型和工程任务,开展针对LEO、SSO、GTO等轨道任务的优化算例求解,提出火箭构型改进方案。
3)开发具有自主知识产权的MDO求解软件平台从长期来讲具有很大的意义和必要性。
[1] 龙乐豪,方心虎,刘淑贞,等. 总体设计(上)[M].北京:中国宇航出版社,1993.
[2] Sobieszczanski-Sobieski J. Multidisciplinary design optimization: an emerging new engineering discipline[R].NASA Technical Memorandum 107761, 19930018069, 1993.
[3] 吴魁,华楠,弓川锦,等.运载火箭总体多学科协同优化平台方案研究[J]. 宇航学报, 2009,30(6):2072-2076.
[4] Martins J R R A, Lambe A B. Multidisciplinary design optimization: a survey of architectures[J]. AIAA Journal, 2013, 51(9):2049-2075.
[5] 龚春林,谷良贤,粟华. 亚轨道重复使用运载器总体多学科优化方法[J]. 固体火箭技术,2012, 35(1):5-10+16.
[6] 王晓青,王小军,王国辉. 空射运载火箭多学科优化设计[J]. 导弹与航天运载技术,2008(5):1-5.
[7] 马英,何麟书. 协同优化在固体弹道导弹概念设计中的初步应用[J]. 固体火箭技术,2008,31(4):313-316.
[8] 王俊峰,胡冬生,张普卓,等. 基于多学科优化平台的运载火箭集成设计技术研究[J]. 导弹与航天运载技术,2015(4):1-4.
[9] 李海燕. 面向复杂系统的多学科协同优化方法研究[M]. 沈阳:东北大学出版社, 2013.
[10] Duranté N, Dufour A, Pain V, et al. Multidisciplinary analysis and optimisation approach for the design of expendable launchers[C]//10thAIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Albany, New-York, USA. 2004.
[11] Balesdent M, Bérend N, Dépincé P, et al. A survey of multidisciplinary design optimization methods in launch vehicle design[J]. Structural & Multidisciplinary Optimization, 2012, 45(5):619-642.
[12] 王振国. 飞行器多学科设计优化理论与应用研究[M]. 北京:国防工业出版社,2006.
[13] 秦旭东,容易,王小军,等. 基于划代研究的中国运载火箭未来发展趋势分析[J]. 导弹与航天运载技术,2014(1):1-4.
[14] 刘竹生,孙伶俐. 航天运输系统发展及展望[J]. 中国科学:技术科学,2012(5):493-504.
[15] 何巍,刘伟,龙乐豪. 重型运载火箭及其应用探讨[J]. 导弹与航天运载技术,2011(1):1-5.
An Overview of Multidisciplinary Optimization Method in Launch Vehicle Design
LIU Zhu-sheng1, ZHANG Bo-rong2
(1.China Academy of Launch Vehicle Technology, Beijing 100076, China 2.Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)
Launch vehicle design is a system engineering process that contains multiple disciplines. In the process of system design, multiple disciplines need to be taken into consideration, including trajectory, aerodynamics, attitude control as well as their coupling effects. Multidisciplinary optimization (MDO) method establishes an approximate model, which could be one-level or multi-level, and can effectively approach the best solution by using appropriate algorithm. In this work, the development of MDO method is systematically introduced, and several classical MDO methods are presented as well as its software platform and one application example. The value of MDO’s application and future development in China’s launch vehicle industry are stressed in the end of this paper.
Multidisciplinary Optimization (MDO); Launch vehicle design; Launch vehicle configuration optimization
2017-05-27;
2017-06-23
刘竹生(1939- ),男,中国科学院院士,主要从事运载火箭总体设计研究。
V421.1
A
2096-4080(2017)02-0001-06

