基于ABAQUS的复合材料网格筒分层破坏分析

李 昊， 赵 川， 张 娇， 周 静， 杜 冬

(上海卫星工程研究所，上海 201108)

基于ABAQUS的复合材料网格筒分层破坏分析

李 昊， 赵 川， 张 娇， 周 静， 杜 冬

(上海卫星工程研究所，上海 201108)

复合材料网格筒结构由于极优的高比强度及比刚度特性，在运载火箭、飞机、卫星等航空航天结构中得到广泛应用。采用ABAQUS对复合材料网格筒结构进行精细化建模，详细分析了复合材料网格筒中的应力分布、分层破坏形式，研究了网格分层破坏出现的位置及对其整体刚度的影响。对网格筒桁条交界处的应力进行详细分析，研究了工艺缺陷对其破坏模式的影响。根据整体分析结果及局部分析结果，设计了承载能力为3500kN，质量为30kg的复合材料网格筒结构。研究成果将为复合材料结构网格筒的分析及设计提供参考。

复合材料；网格筒；分层破坏

0 引言

随着复合材料设计及工艺技术的不断发展，在航空航天等所有对质效比有高要求的场合，几乎无一例外地选用了碳纤维增强复合材料作为主要的结构材料。复合材料网格结构是一种网状筋条结构，网格复合材料结构是由金属网格结构发展而来, 网格结构的突出优点是较高的强度/质量比, 因此备受关注。这使得网格结构广泛应用于航空航天领域。目前已有多种类型网格结构在航空航天领域应用, 如战略导弹级间段、仪器舱、空间飞行器舱体、箭与卫星对接框、整流罩等部件[1]。

复合材料网格结构初期作为复合材料蒙皮结构的增强结构，通过网格结构的抗屈曲特性增加复合材料蒙皮结构的抗局部屈曲特性，进而实现具有较高薄膜刚度和弯曲刚度的蒙皮结构[2-3]。近年来，随着复合材料蜂窝板的工艺技术不断发展，复合材料蜂窝板的质效比特性已经能够达到甚至超越网格结构的质效比，而蜂窝板的材料工艺成本要远小于网格加筋板。因此，各国的研究者都竭力对复合材料网格结构进行深度优化研究，以充分挖掘网格结构的潜能[4]。

复合材料网格筒结构是网格结构应用的成功范例，典型的网格筒形式包括带蒙皮网格筒和不带蒙皮网格筒。目前复合材料网格筒结构的结构参数优化研究已趋于成熟，多年来国内外学者对网格筒结构的众多参数包括蒙皮厚度、纵筋的数目、环筋的数目、缠绕角度以及筋截面的高宽比等的影响规律进行了详细研究[5]。网格筒结构参数的优化研究使得理想情况下其整体刚度、整体抗屈曲能力及局部抗屈曲能力得到显著提升。然而，由于网格筒结构中横向筋、纵向筋及斜筋存在交叉，交叉部位不可避免地出现纤维架空、层间裂纹及空隙率较大等局部缺陷。实验中发现，在交叉点局部缺陷的存在往往使得复合材料网格筒在交叉部位出现分层破坏，导致网格筒的实际承载能力小于设计承载能力。因此，怎样在网格筒的设计分析中预测有可能的分层破坏模式，是预测网格筒真实承载能力亟待解决的问题。

本文创新性地利用了线性traction-separation理论，结合有限元方法研究复合材料网格筒的局部分层破坏现象，解决了复合材料网格筒的实际承载能力预测问题。

1 复合材料层间强度本构模型

复合材料的层间力包括法向力tn及两个相互垂直方向的层间剪切力ts、tt。复合材料层间破坏模式主要包括层间拉伸破坏及层间剪切破坏，复合材料层间相对位移为δn、δs及δt。假设复合材料为线弹性材料，则复合材料层间相对位移与层间应力之间的关系为：

(1)

其中K为复合材料界面的刚度矩阵。为了简化计算，本文假设复合材料界面的法向与切向之间相互独立，即法向的相对位移不会引起切向力，同理切向相对位移不会引起法向力。因此，刚度矩阵中的耦合项全部为0， 式(1)简化为：

(2)

在实际的受力过程中，当复合材料的层间法向力达到一定值后，材料内部将发生初始破坏。本文考虑了两种层间初始破坏判据，分别为最大应力准则及平方和应力准则。最大应力准则指层间界面的任一应力与其层间极限强度的比值大于1时，即认为层间界面发生初始破坏。最大应力准则表达式为：

(3)

(4)

当复合材料的层间界面应力满足初始破坏条件后，应定义材料的损伤演化过程。本文假设复合材料的界面分层损伤演化过程为典型的线性软化过程，如图1所示。

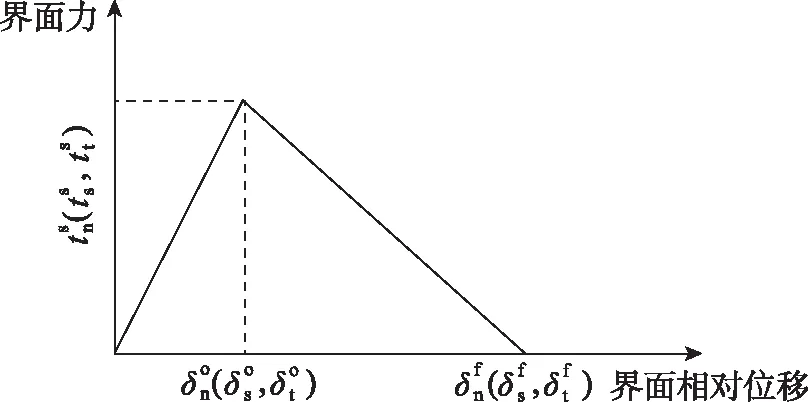
图1 典型线性拉-张本构Fig.1 Standard linear traction constitutive relation of composite interface

损伤演化准则实质是定义在满足初始损伤判据后，复合材料的界面刚度以怎样的速率下降。通常情况下，通过定义一个初始值为0损伤变量D。随着复合材料界面损伤的不断演化，损伤变量D从0单调地增长为1。当损伤变量D的值为1时，即认为层间界面完全破坏，层间应力为0，如式(5)所示：

(5)

2 网格筒有限元模型

本研究以参考文献中优化所得的网格筒作为蓝本，研究网格筒有可能出现的层间分层破坏。网格筒几何模型见图2所示，网格筒高度为1700mm，内径为1200mm，外径为1230mm，斜筋角度为24.5°，斜筋截面尺寸为15mm×6mm；横向筋布置在每个单元中部，横向筋截面尺寸为15mm×2mm。网格筒上下两端分别设置内径为1200mm、外径为1230mm的端框，端框厚度为20mm。

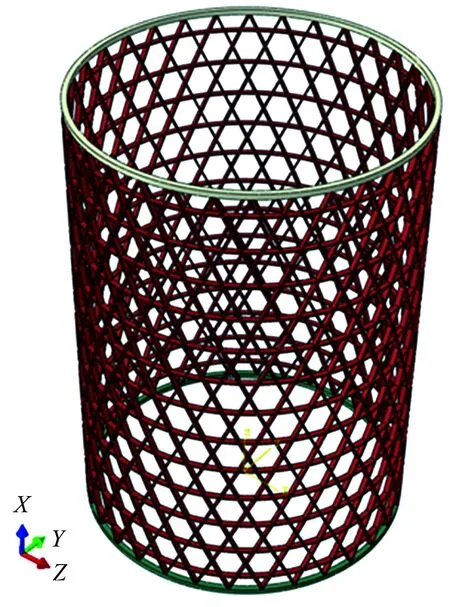
图2 网格筒几何模型Fig.2 Geometric model of composite grid cylinder

本文采用有限元软件ABAQUS建立网格筒模型。为了模拟网格筒在筋厚度方向有可能出现的分层破坏，对网格筒进行理想化处理，将网格筒从筋厚度方向分割成等厚的3个网格筒，每个网格筒筋条的厚度为5mm，见图3所示。本文假设3个网格筒之间通过树脂牢固粘接在一起，分别在3个网格筒的界面之间建立胶结接触属性(cohesivesurface)。界面胶结本构采用非耦合本构关系，见式(2)。本文采用毫米制建模，设定胶界面的法向刚度Knn和界面剪切刚度Kss、Ktt都为10Gpa。网格筒中的基体为高温固化环氧树脂。通常情况下，环氧树脂可以认为是脆性材料，即当其应力达到最大值后，环氧树脂将发生脆性破坏。由于环氧树脂的断裂本构不是本文研究的重点，为了简化计算，本文设置网格筒界面层的刚度退化准则为基于能量的线性刚度退化，并假设断裂能为一个极小值，即层间界面的应力达到其破坏初始应力后，界面立即发生分层破坏。

图3 网格筒分割示意图Fig.3 Partition of grid cylinder

网格筒的筋条材料为T700/环氧树脂体系，上下端框采用铝合金，有限元模型中的材料参数见表1。

表1 材料参数

为了降低计算成本，本文对网格筒模型对称取1/4进行计算。筋条的单元类型为实体壳单元SC8R，上下端框的单元类型为8面立方体减缩积分单元C3D8R(见图4)。模型整体单元数量为67979个SC8R单元及752个C3D8R单元。

图4 网格筒有限元模型及网格划分Fig.4 Finite element model of grid cylinder

3 网格筒有限元分析结果

设置复合材料界面法向剥离强度为10Mpa，界面剪切强度为30Mpa。在网格筒的上端框施加一个向下的位移载荷，采用静态分析步进行分析。当不考虑界面的损伤演化时，界面牢固粘接并不发

生分层破坏。不考虑损伤时网格筒在上端框竖向载荷作用下上端框圆心的位移载荷曲线见图5所示。1/4网格筒竖向最大承载能力为333.75kN，则网格筒整体承载能力为1335kN。当上端框位移为2mm时，1/4上端框所承受的力约为110kN，则网格筒整体承力约为440kN。上端框竖向位移为2mm时网格筒纤维方向应力的计算结果见图6所示。图6中网格筒上端框向下位移量为2mm，应力云图显示斜筋中主要为压应力，而横向环筋中主要为拉应力。横向环筋中最大拉应力为245.1Mpa，而斜筋交叉位置处压应力较大，约为-200Mpa。斜筋与上下端框的连接处出现较大的局部应力集中，最大压应力为-334.8Mpa。

图5 无分层破坏时竖向载荷作用下承力筒上端框圆心位移载荷曲线Fig.5 Load-displacement curve corresponding to the top middle point of the grid cylinder with no delamination

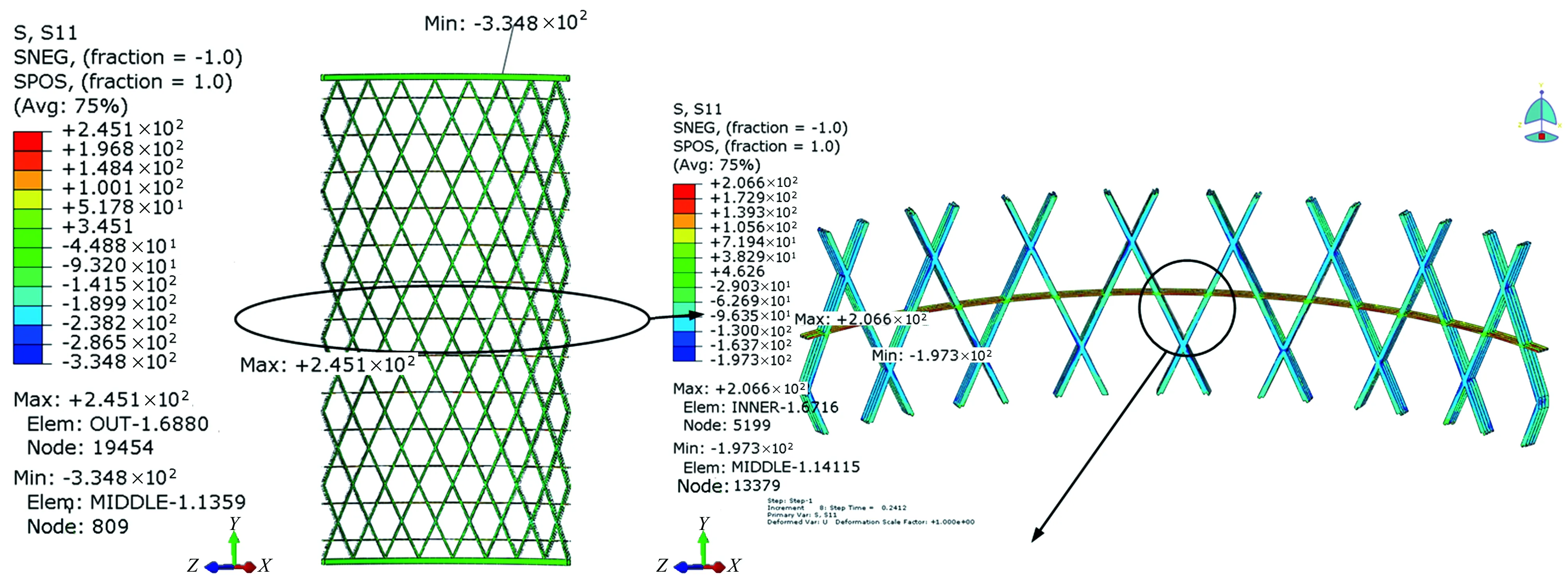
图6 不考虑分层损伤网格筒纤维方向应力云图Fig.6 Contour map of stress S11 along the fiber in the grid cylinder with no delamination

当对网格筒的两个界面层施加最大应力准则并设置脆性损伤演化特性时，网格筒上端框位移为1mm时，两个界面层发生破坏区域云图见图7所示。图7中的变量CSDMG对应式(5)中的损伤变量D。当变量CSDMG为1时，表示界面层发生分层，当CSDMG为0时，表示界面层未发生分层破坏。由于本文认为树脂基体发生脆性断裂，因此变量CSDMG的值为0或1。图7显示，网格筒在几乎所有筋条交叉的部位发生了分层破坏，说明在交叉部位由于纤维走向不同，因此交叉部位的应力状态较为复杂，导致交叉部位出现应力集中。本文的有限元模型为理想模型，而实际情况中，由于筋条交叉部位通常出现纤维架空，纤维局部堆积、纤维弯曲及层间裂纹等缺陷，因此在实际工程中筋条交叉部位在复杂应力的作用下更加容易出现分层破坏。

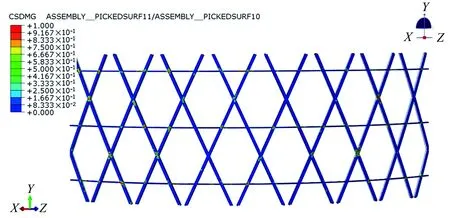
(a)界面1

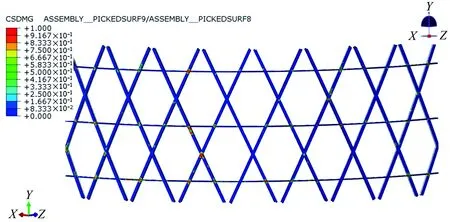
(b)界面2

当考虑层间损伤，上端框竖向位移为2mm时，网格筒的纤维方向应力云图见图8所示。计算结果显示发生交叉点局部分层破坏后，网格筒重纤维的应力水平没有发生明显变化。无分层情况下和局部分层情况下的上端框圆心的位移载荷曲线见图9所示。图9中分别给出了采用最大应力准则和平方应力准则时的上端框圆心的位移载荷曲线。分析结果显示两种应力准则对应的计算结果相似；当考虑网格筒发生局部分层破坏时，随着压缩位移的增加，网格筒的竖向刚度出现了小幅度的衰减。

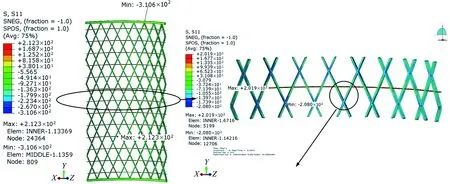
图8 考虑网格筒分层损伤后网格筒纤维方向应力云图Fig.8 Contour map of stress S11 along the fiber in the grid cylinder with delamination

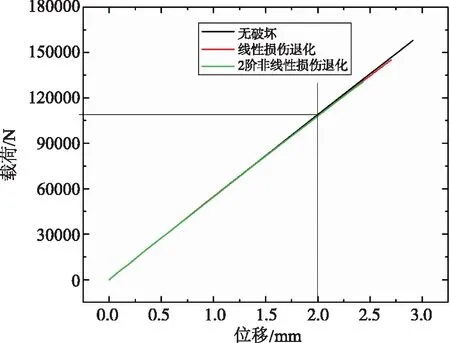
图9 竖向载荷作用下承力筒上端框中心点位移载荷曲线Fig.9 Load-displacement curve of the top middle point of the cylinder

4 结论

本文基于ABAQUS中的界面粘接接触功能，模拟分析了复合材料网格筒结构在受力过程中可能出现的局部分层破坏。以中俄合作项目设计的网格筒作为输入文件，将网格筒沿着筋条厚度方向分为若干层，并在层与层之间建立界面。分析结果显示，在竖向载荷的作用下，网格筒在筋条交叉的部位应力状态较为复杂，应力水平较筋条其他部位相对较高。当对筋条界面设置损伤演化准则后，分析结果显示复合材料网格筒在筋条交叉处将出现局部的分层破坏，并且分层区域随着载荷的增加不断扩展。在分层破坏的影响下，网格筒的竖向刚度出现了小幅下降。复合材料网格筒的筋条在交叉处不可避免地会出现一定的纤维弯曲、纤维堆积、纤维架空及初始分层等缺陷，这些缺陷的存在将进一步增加网格筒出现分层破坏的可能性，降低网格筒的可靠性及安全裕度。本文的分析方法及分析结果将为网格筒的设计提供新的工具和指导。

[1] 陈小平，杨杰，刘建超. 复合材料网格结构的研究现状[J]. 宇航材料工艺,2009,39(2)：6-11.

[2] 李超，景宽. 复合材料网格的研制发展历程[J]. 纤维复合材料，2004，21(4):47-51.

[3] 张成. 复合材料斜交网格机身结构[J]. 科技创新导报，2015，12(8):9-10.

[4] 辛星. 复合材料网格圆柱结构减重优化设计[J]. 固体火箭技术,2013,36(2):243-245+260.

[5] 张昌天，周涛. 复合材料等网格圆筒结构刚度的优化设计[J]. 高科技纤维与应用, 333(3):10-13+23.

Delamination Damage Analysis of Composite Grid Cylinder Based on ABAQUS

LI Hao, ZHAO Chuan, ZHANG Jiao, ZHOU Jing, DU Dong

(Shanghai Institute of Satellite Engineering, Shanghai 201108,China)

Composite grid cylinders are widely applied in launchers, aircrafts and satellites, due to their high specific strength and specific stiffness. In this study, the commercial finite element code ABAQUS is employed to investigate the stress distribution and the delamination damage of composite grid cylinder. The position where the delamination starts and the influence of delamination damage on the stiffness of the grid cylinder are predicted and discussed. Meanwhile, the stress near the intersection of the stringers is investigated in detail and the influence of the manufacturing technology is studied. Based on the prediction and investigation, in this study we designed a composite grid cylinder, the load bearing capacity of which is 1335 kN, and the mass is 30kg. The prediction and discussion in this study are of value for the designing of composite grid cylinders.

Composite; Grid cylinder; Delamination

2017-05-15；

2017-06-06

李昊 (1987-)，男，硕士，工程师，主要从事卫星结构及机构设计。E-mail：hithaoli@126.com

V41

A

2096-4080(2017)02-0046-07