上面级适应初始大偏差轨道在线规划策略研究

王传魁， 郑莉莉， 解永锋， 周文勇， 陈 益， 安雪岩

(北京宇航系统工程研究所，北京 100076)

上面级适应初始大偏差轨道在线规划策略研究

王传魁， 郑莉莉， 解永锋， 周文勇， 陈 益， 安雪岩

(北京宇航系统工程研究所，北京 100076)

提出了一种上面级适应初始轨道大偏差的轨道在线规划策略，在上面级初始轨道参数存在较大偏差情况下，通过轨道在线规划，将规划后的控制诸元上传至上面级，使得上面级按照新的轨道飞行，将卫星送入目标轨道或大幅减小卫星入轨偏差，减小上面级由于入轨偏差修正过程中燃料的消耗。该策略可以广泛应用在上面级直接入轨发射MEO、GEO卫星等典型中高轨任务中。

上面级;轨道;在线规划;策略

0 引言

上面级是一种由基础级运载器发射进入准地球轨道或地球轨道，能够进一步将有效载荷从准地球轨道或地球轨道送入预定工作轨道或预定空间位置的具有自主独立性的飞行器。在基础级将上面级和载荷组合体送入过渡轨道后，带有独立动力和控制系统的上面级接力工作，开始变轨将载荷直接送入目标轨道[1]。基础级分离上面级时的入轨偏差，由上面级通过制导控制和推进剂余量进行修正，但若此偏差过大，则按照射前装定的轨道诸元，导致上面级推进剂消耗殆尽，卫星无法正常入轨。带有遥控功能的上面级可在基础级火箭入轨后存在大偏差的情况下通过地面进行在线轨道规划，上传新的轨道控制诸元，使上面级按照新的轨道飞行，将卫星送入目标轨道或大幅减小卫星入轨偏差，提高上面级对初始轨道偏差的适应能力。

1 上面级轨道方案与制导方法

在直接入轨发射卫星时，上面级采用两次变轨方案(以发射GEO轨道卫星为例)：第一次变轨在上面级卫星组合体与基础级火箭分离后进行，此刻通过加速抬高转移轨道远地点高度；第二次变轨在转移轨道远地点进行，目的是抬高轨道近地点以圆化轨道，并压低或者修正轨道倾角，最终将卫星送入目标轨道，变轨示意如图1所示[2-3]。正常情况下，上面级控制完全自主进行，无需地面干预。上面级入轨初始偏差较大的情况下，需要通过地面上行遥控功能进行轨道在线规划。

图1 飞行轨道示意图Fig.1 Schematic figure of orbit

上面级第一次变轨沿速度方向推进[4]，当达到预定半长轴时关机，滑行至过渡轨道远地点后采用迭代制导进行变轨。迭代制导是一种直接自适应制导方式，通过当前的速度位置和终端约束实时计算程序角[5]。直接制导方式虽然是一种基于两点边值的直接制导方式，对初始轨道偏差有一定适应能力，但在基础级入轨偏差的情况下，上面级实际飞行轨道会偏离原标准轨道，再按照原标准轨道给定的诸元(点火条件和关机条件)进行制导，从能量角度出发，不是一种最优的变轨方案。直接制导本身不具有自动寻优改变点火条件和入轨诸元的能力，以其直接制导原理的自适应能力，虽然在初始轨道偏差情况下能够保证入轨精度，但却需要较多的推进剂；而轨道在线规划，是在同样条件下，更新一条优化的轨道，形成新的制导诸元，对于第二次变轨而言，没有初始偏差，因此能够实现对重新规划轨道的复现，满足卫星入轨精度要求。

2 大偏差应对策略设计

2.1 初始偏差分析

综合研究分析，基础级火箭故障情况下容易出现远地点高度、轨道倾角等多项入轨参数不满足指标要求，因此上面级轨道在线规划主要针对入轨远地点高度、轨道倾角大偏差进行分析。

2.2 应对策略设计

上面级的轨道在线规划策略与上面级的变轨策略和制导控制方式紧密相关，不同的轨道，上面级制导自主控制对基础级入轨偏差的适应能力和敏感程度是不同的，不同的任务在线规划策略也不同，本文以上面级两次变轨发射GEO卫星为例。

在基础级出现较大偏差的情况下，上面级需要重新开展轨道设计，在轨道大偏差工况下寻找新的飞行轨迹，以满足卫星入轨参数要求或者尽量缩小偏差，将新轨迹的部分特征点参数(第二次点火时刻真近点角、第二次关机时刻半长轴、第二次关机时刻偏心率、第二次关机时刻轨道倾角、第二次关机时刻近地点幅角、第二次关机时刻升交点经度、第二次关机时刻真近点角)重新作为制导控制诸元上传至上面级控制中心，使得上面级按照新制导诸元进行飞行控制以实现制导控制收敛，满足高精度控制要求。上面级两次变轨发射GEO卫星，通过自主改变第一次变轨时间来修正基础级入轨远地点高度偏差量，通过在线轨道规划重新设计第二滑行段、第二次主动段轨道来满足制导的需求，从而实现制导的快速收敛，达到高精度入轨的目的。

2.3 轨道迭代计算

轨道设计采用调整点火时刻t1、机动时长t2和推力偏航角修正量δψ来最终满足卫星轨道参数[6]，计算卫星分离后的弹道倾角Oa、轨道半长轴a和轨道倾角i，采用牛顿迭代算法进行求解，迭代关系式为：

判断卫星入轨参数是否满足如下条件：

其中，Oa为当前弹道计算卫星入轨时刻弹道倾角；a为当前弹道计算卫星入轨时刻轨道半长轴值，aT为卫星发射轨道半长轴目标值；aeps为卫星发射轨道半长轴控制精度；i为当前弹道计算卫星入轨时刻轨道倾角，iT为卫星发射轨道倾角目标值，ieps为卫星发射轨道倾角控制精度；Oa为t1的函数，a为t2的函数，i为δψ的函数。

3 轨道在线规划设计依据

根据上面级入轨时刻的轨道倾角、远地点高度偏差判断是否开展轨道在线规划工作，偏差范围可以采用如图 2所示的示意图进行设计，其中A、B、C、D这4个分区分别代表了不同的上面级入轨偏差范围，图中黑色点线代表综合考虑燃料可用量后轨道在线规划能够适应的远地点高度偏差下限，不同分区对应在线规划策略如表1所示。

图2 轨道在线规划依据示意图Fig.2 Schematic figure of on-line trajectory planning basis

序号分区入轨偏差情况规划策略规划后结果12AB 上面级入轨轨道倾角偏差绝对值小于x1°,远地点高度负偏差小于x3km 上面级入轨轨道倾角偏差绝对值在x1°～x2°之间,远地点高度负偏差小于x3km不进行规划,制导自主适应 以第一次变轨结束后的轨道参数和上面级质量参数作为输入,以卫星要求轨道参数作为目标量,重新进行弹道迭代计算 满足卫星入轨精度要求3C 上面级入轨轨道倾角偏差绝对值大于x2°,远地点高度负偏差小于x3km 以第一次变轨结束后的轨道参数和上面级质量参数作为输入,根据推进剂剩余量迭代调整卫星入轨轨道倾角弹道迭代目标量(使得目标量尽量满足卫星要求,保持其他参数要求不变),重新进行弹道迭代计算 卫星入轨轨道倾角超差,轨道倾角满足要求4D 上面级入轨远地点高度负偏差大于x3km 以第一次变轨结束后的轨道参数和上面级质量参数作为输入,以当前轨道倾角作为弹道迭代目标量,根据推进剂剩余量迭代调整卫星入轨半长轴弹道迭代目标量(使得目标量尽量满足卫星要求),重新进行弹道迭代计算 卫星入轨轨道半长轴超差,轨道倾角满足要求或超差

注：其中x1、x2、x3为正有理数。

4 仿真计算与结果分析

4.1 轨道偏差工况

以发射GEO轨道卫星任务为例，给出上面级入轨点理论轨道设计标称值与实际入轨参数见表2所示,入轨偏差情况下上面级第一次工作结束后轨道参数如表3所示。

表2 上面级入轨偏差工况表

表3 上面级一次变轨结束后轨道参数

4.2 轨道在线规划设计

按照第2节描述的入轨偏差应对策略，开展在线轨道规划，规划后需要上传的新控制诸元主要参数如表4所示，规划后理论卫星入轨参数如表5所示。

表4 在线规划后需要上行替换的轨道控制诸元

表5 在线规划后理论卫星入轨参数

注：因0倾角圆轨道的特殊性，这里不给出近地点幅角、升交点经度和真近点等具有奇异性的参数。

4.3 仿真结果

按照4.1节偏差工况进行制导仿真，上面级第一变轨段按照制导关机后，第二变轨段仍按射前装定的诸元进行制导控制，卫星入轨参数见表6所示。

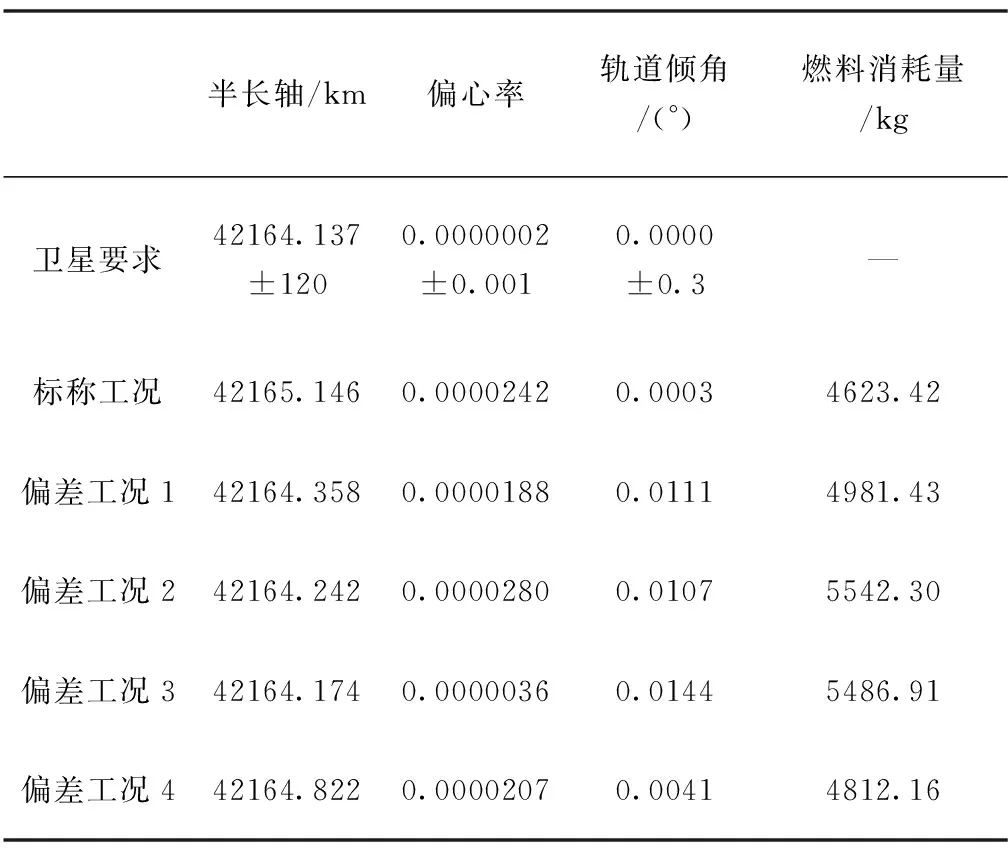
表6 不进行在线规划制导仿真卫星入轨参数

基于火箭射前上面级轨道控制诸元进行仿真，第二变轨段制导飞行控制程序角变化趋势如图3～图6所示, 对比实施在线规划前后的飞行程序角，可以看出如果不进行轨道在线规划，上面级根据偏差大的诸元进行制导，飞行姿态角变化较为剧烈，不利于箭上飞行姿态控制；而进行规划后飞行姿态平滑，更利于箭上实施，飞行姿态控制简单。

图3 工况1制导仿真俯仰角和偏航角变化曲线Fig.3 Simulation curves of pitch angle and yaw angle for condition one

图4 工况2制导仿真俯仰角和偏航角变化曲线Fig.4 Simulation curves of pitch angle and yaw angle for condition two

图5 工况3制导仿真俯仰角和偏航角变化曲线Fig.5 Simulation curves of pitch angle and yaw angle for condition three

图6 工况4制导仿真俯仰角和偏航角变化曲线Fig.6 Simulation curves of pitch angle and yaw angle for condition four

4.4 小结

对表 4、表6和表7进行统计后，绘制上面级轨道在线规划前和规划后卫星入轨精度和上面级燃料消耗相对标称工况对比情况,如表8所示。从表中可见，在上面级入轨较大偏差情况下，轨道在线规划可以显著提高入轨精度和节省燃料消耗。

表7 采用在线规划后控制诸元制导仿真卫星入轨参数

表8 轨道在线规划前后入轨精度和燃料消耗相对标称工况对比表

5 结论

本文针对上面级直接入轨发射卫星技术，研究了上面级适应入轨大偏差情况下轨道在线规划策略，制定了规划依据和方法，经过数值仿真可见策略有效，方法可行，能够有效提高上面级对初始入轨偏差的适应性。

[1] 余梦伦.末级技术对提高运载火箭性能的作用[J].导弹与航天运载技术,1993(2): 12-20.

[2] 余梦伦.地球同步卫星发射轨道的设计[J].中国空间科学技术,1983,3(2): 1-8.

[3] 余梦伦.地球同步卫星的发射轨道的选择[J].中国空间科学技术,1990,10(1): 21-27.

[4] 王传魁,周文勇,陈益,等.基于转动矩阵法的火箭上面级机动程序角设计[J].导弹与航天运载技术,2016(2): 8-12.

[5] 陈新民,余梦伦.迭代制导在运载火箭上的应用研究[J].宇航学报,2003,24(5): 484-489.

[6] 贾沛然，陈克俊，何力.远程火箭弹道学[M].长沙：国防科技大学出版社,2009： 124-138.

Research on On-line Trajectory Planning Strategy for Upper-stage to Adapt Initial Large Deviation

WANG Chuan-kui, ZHENG Li-li, XIE Yong-feng, ZHOU Wen-yong, CHEN Yi, AN Xue-yan

(Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)

This paper provides a strategy of upper-stage on-line trajectory planning to adapt initial large deviation. When there is deviation of the upper-stage initial injection orbit parameters, we can send the replaned control data to the upper-stage with the on-line trajectory planning. And the upper-stage can fly in a new optimized trajectory, so as to put the satellites into the target orbit precisely, or to decrease the deviation and fuel consumption of the maneuver. This strategy can be extensively used for direct orbit injection missions to the high medium-earth-orbit， such as MEO(medium earth orbit) and GEO(geostationary orbit).

Upper-stage vehicle；Trajectory；On-line planning；Strategy

2017-03-30；

2017-05-17

国家高技术研究发展计划(2014AA2644)

王传魁(1985- )，男，硕士，工程师，主要从事运载火箭上面级轨道设计方面研究。E-mail:chuankui.w@163.com

V412

A

2096-4080(2017)02-0012-08