提高轴孔连接结构承载能力的设计方法

刘文章，何景武，严斌，吴文伟

（1.中国船舶科学研究中心，江苏无锡214082；2.北京航空航天大学航空科学与工程学院，北京100191）

提高轴孔连接结构承载能力的设计方法

刘文章1，何景武2，严斌1，吴文伟1

（1.中国船舶科学研究中心，江苏无锡214082；2.北京航空航天大学航空科学与工程学院，北京100191）

文章针对轴孔连接结构提出了一种改善轴孔接触特性来提高承载能力的方法。以工程中通用的螺栓连接结构为例，建立接触分析模型，应用Persson接触理论和优化分析方法，通过优化耳片孔接触面的曲面形状和曲面参数实现了降低轴孔接触区最大接触应力及改善其分布梯度的目的。针对优化后的耳片孔接触曲面设计结果，利用有限元素法建立了螺栓耳片连接结构模型，分析验算了接触应力。结果表明，优化分析的解析法和有限元素法的计算结果基本一致。连接结构优化设计后，接触区最大应力降低50%以上，应力分布梯度明显改善，提高了其承载能力。

轴孔连接结构；Persson接触理论；接触应力；结构优化；承载能力

0 引言

轴孔连接在船舶等工程结构设计中应用非常普遍，是机械结构中重要的传力部件，比如螺栓与耳片。由于其本身的结构特点，承力时往往是外力通过轴直接施加在孔边上，孔边会因为挤压而出现接触应力分布集中的现象，导致其承载能力不高，而且在动态载荷作用下，容易造成局部点的接触受损。因此孔边接触区域往往会成为影响整个连接结构承载能力的关键部位。

但是，到目前为止，国内外大部分的研究主要集中在接触应力的求解方法上，对改善接触应力分布的措施与方法研究不多。参考文献[1]提出了一种利用能量守恒来计算接触应力的方法。参考文献[2-3]主要针对连接件接触应力分布的求解领域。参考文献[4-5]利用有限元方法来模拟计算接触应力。参考文献[6-7]提出了一种通过改变物体形状来降低接触应力的构想，但是没有形成系统条理的改进方法。

本文建立了一种系统地改善轴孔连接结构接触区应力分布的方法。建立连接结构的平面接触模型，确定接触应力的理论求解方法，通过改变耳片孔接触面的曲面形状并优化曲面参数，使耳片孔边接触区的最大应力及应力分布梯度得到降低，如图1所示，接触区应力分布由初始图线1变为目标图线2。计算轴孔连接结构接触应力的有限元解，与理论解误差对比，验证优化设计的准确性。通过上述过程来探究耳片孔接触面几何构型对接触区应力分布的影响，达到提高承载能力的目的。

图1 优化设计目标示意图Fig.1 Schematic diagram of optimal target

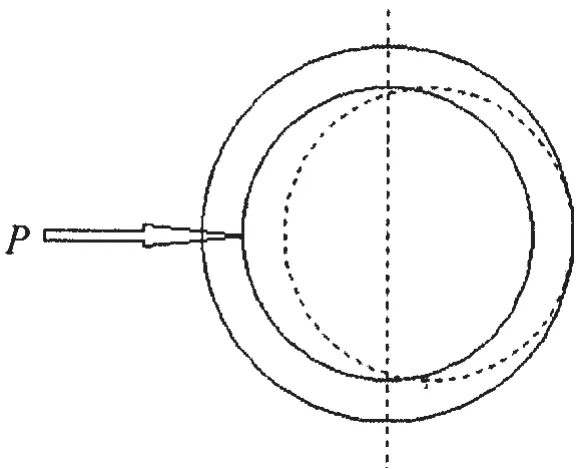
图2 轴孔连接结构的接触示意图Fig.2 Schematic diagram of contact progress

1 平面接触模型的建立

1.1 接触过程分析

通常在使用中，按照配合精度要求，螺栓轴和耳片孔是间隙配合，但是配合间隙很小，配合表面在无变形时已经相当接近地贴合在一起。外力载荷P一般通过螺栓轴直接挤压耳片而传递载荷，随着外部载荷的逐步增加，轴孔接触由线接触（图2虚线所示）迅速扩展到面接触，使其与轴孔本身的有效几何尺寸相当。这一边界非线性的协调接触过程，不适合弹性半空间的假设，不满足Hertz接触理论的适用条件[8-9]，需要用Persson接触理论求解。

1.2 平面接触模型

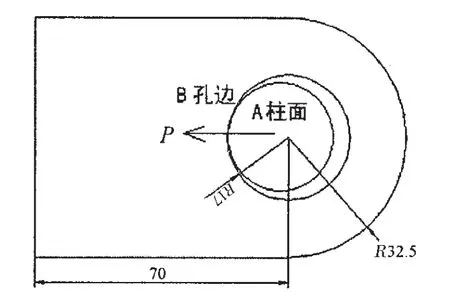
图3 平面接触模型Fig.3 Model of plane contact

图4 实例几何模型示意图Fig.4 Geometric model

在载荷作用下的接触过程，沿轴孔连接结构的轴向基本不变，连接结构轴向尺寸相对较大且受力沿轴向变化较小，因此假定轴与孔的应力状态为平面应变状态，建立如图3的平面接触模型，A为螺栓轴截面，B为耳片截面。以某结构物设计中所应用的螺栓耳片结构为例，如图4所示。

假定螺栓轴与耳片孔的配合精度为H8/f7[10]，平面接触模型中的几何参数为：孔基本尺寸17，孔上偏差ES=0.027，轴下偏差ei=0.034，最大间隙△R=ES-ei=0.061 0，计算中设定螺栓轴半径rA=16.939，耳片孔半径rB=17.000。材料参数为：弹性模量EA=210 GPa，EB=195 GPa，泊松比νA=νB=0.3。外部载荷为：P=285.3 kN。

2 接触应力的理论求解

应用改进的Persson接触理论[11-12]，求解轴孔连接结构的接触应力分布规律。改进的Persson接触理论，有以下两个假设：（1）忽略接触区径向位移和切向位移间的耦合作用；（2）接触区法向最大变形与径向位移之间的关系满足刚体接触的几何刚度条件。忽略接触区域的摩擦作用[4]，轴孔连接结构接触应力的计算，符合Persson理论的两个假设。

轴A与孔B在点1处配合接触，在A的轴心Oe处作用一外部集中力P，接触区圆弧对应弧度为2ε，接触区圆弧关于外力作用线对称分布，如图5所示。

载荷P与接触半弧度ε之间的关系[11-12]如下：

图5 Persson理论模型示意图Fig.5 Schematic diagram of Persson model

接触压力分布p（y）与变量角φ关系[11-12]如下：

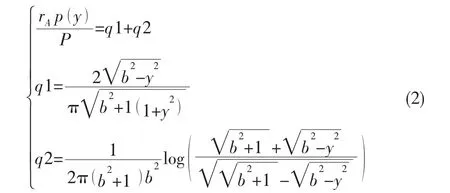
图6 初始模型的接触应力分布图Fig.6 Contact stress distribution of initial model

（1）式是关于ε的非线性方程，在外部载荷P已知的情况下，通过数值分析方法求得。代入（2）式即可计算得到接触应力理论解。未优化的初始模型接触区应力p（y）随角度φ的变化规律，如图6所示。

接触弧度参数b=tan（ ε/2）=0.163 0，接触应力最大值pmax=33 292.0 kPa。

3 耳片孔的优化设计

3.1 优化设计模型

接触应力大小与两个因素有关：（1）接触点的曲率；（2）接触点的数目。

（1）接触点曲率：如表1所示，rA不变，rB变小，接触区域弧度变大，最大接触应力变小，符合优化方向。

（2）接触点数目：接触点越多，承载区域会越大，接触应力就会越分散，最大接触应力也会越小，符合优化方向。

螺栓一般为标准件，选择耳片孔为优化对象。设计中选择耳片孔边接触曲面为便于精加工的椭圆形状，符合上述两点优化方向要求。建立优化设计模型，通过优化耳片孔的曲面参数，使接触区的接触应力最大值pmax最小。

优化设计模型表述为：

表1 接触曲率变化对pmax影响表Tab.1 Effect of contact curvature on pmax

如图7所示，轴A圆的方程为：

耳片孔B椭圆的方程为：

式中：R为圆的半径，c为圆心到X轴的距离，a为椭圆的短半轴，b1为椭圆的长半轴。

轴A半径尺寸R=16.939。根据配合精度，椭圆孔短轴a=17.00固定，选择长轴b1为优化设计变量，b1不同，对应接触点的曲率就会变化。

3.2 优化设计方法

圆与椭圆接触，如图7所示，最初接触点为C和D。外部载荷P平均分配到两个接触点上。

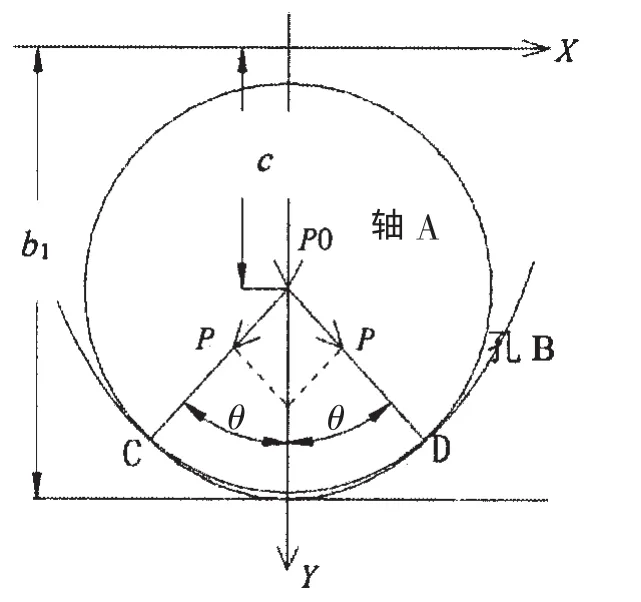
图7 圆与椭圆接触示意图Fig.7 Schematic diagram of contact between circle and ellipse

便于计算方便，设计变量由变量b1换算为接触点和Y轴的角度θ。

圆与椭圆在C点切线斜率相等，

C点位于椭圆上，

（7）式和方程（8）得到θ与b1关系式：

接触点处的椭圆曲率半径为

设计变量θ值变化，最初接触点C和D都会变化，C和D处相应的曲率随之变化，计算得到C和D处各自的接触应力分布。

θ值不同，C和D各自接触区大小不同，分为C和D接触区域是否重合两种情况。

（1）接触区未重叠情况的接触应力求解：

初始接触角θ大于等于各接触点接触弧度ε，即θ≥ε，如图8所示。此时两个接触点的应力分布没有重叠。

两个接触区各自的应力分布分别为：

θ=30°时的接触应力分布图，如图9所示。

图8 未重叠接触角度示意图Fig.8 Schematic diagram of contact angle without overlap

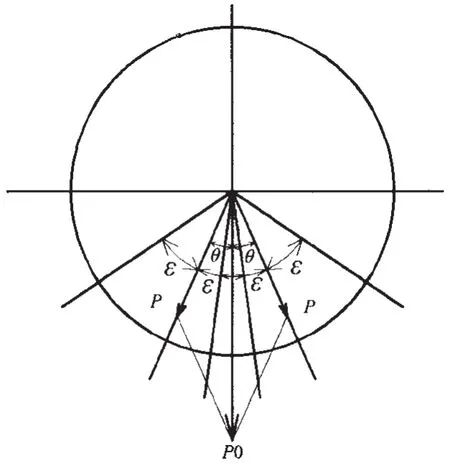
图10 重叠接触角度示意图Fig.10 Schematic diagram of contact angle with overlap

图11 θ=22°时接触应力分布图Fig.11 θ=22°:Contact stress distribution

忽略两个接触点接触区的相互影响，计算两个接触区的应力分布。重叠部分，两个区域接触应力相加；未重叠部分，接触应力保持不变。

接触区应力分布为：

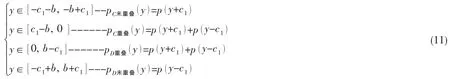
θ=22°时的接触应力分布图，如图11。

（3）优化设计过程：

随着θ值变化，接触区应力首先在两侧单独存在，然后在中间部分重叠。最大应力由大变小，再变大，存在最小值。变化趋势如图12中箭头方向所示。最大接触应力最小情况发生在两个接触区域重叠的情况下。

当x=0时的叠加应力p（0）与以C、D点为中心的单侧最大应力相等时，最大接触应力最小，满足设计目标，即：p（0）=max p（y），计算可得最优解θ值和最优椭圆曲线参数b1。

图12 θ=22°-15°变化时接触应力变化图Fig.12 Change of contact stress when θ=22°-15°

3.3 最优结果

如表2所示，最优解θ=21.096 3°，最优椭圆曲线参数b1=17.070 3，最大接触应力值降低了58.7%，优化效果非常显著。

表2 优化设计结果Tab.2 The optimization design results

4 有限元解和理论解误差对比

4.1 有限元建模[13-14]

接触问题是一种极度不连续的高度边界非线性问题。两个面接触，必须施加相应的约束关系，并判断接触面积和接触压力。两个面分开，则没有接触存在，就必须移走相应的约束。接触问题的特点决定了其通常采用增量法求解，采用罚函数法将界面条件引入到求解方程。本文应用Abaqus软件，采用Newton-Raphson法求解非线性方程。

对初始未优化模型（圆与圆接触）和优化后模型（圆与优化设计得到最优参数解的椭圆接触）两种情况进行建模。采用平面应变简化，忽略接触面摩擦[4]，建立1/2对称模型，对称面上施加对称边界条件，即U1=UR2= UR3=0，其他周边边界为固支。

统一采用CPE4R单元，结构性网格划分。在接触面附近对网格进行加密，以获得良好的计算结果。选择面面接触，A为主面，B为从面，小滑移，无摩擦。加载方式为圆A圆心位置竖直外力P0=283.5 kN。图13左图未优化模型中Circle A为圆A，单元类型为quad，单元数为526；Circle B为圆B，单元类型为quad，单元数为2 411。图13右图优化模型中Circle A为圆A，单元类型为quad，单元数为848；Ellipse为椭圆B，单元类型为quad，单元数为3 308。

图13 有限元模型（左图为未优化，右图为优化）Fig.13 FEM models(left:not optimal,right:optimal)

4.2 有限元计算结果

计算分析得出两种模型的接触应力云图，如图14所示。计算得出两种模型的接触应力曲线图，如图15所示，p为接触应力值，X为从圆最下端位置起沿圆弧向上的距离值。

图14 接触应力云图（左图：未优化，右图：优化）Fig.14 Contact stress contours(left:not optimal,right:optimal)

图15 接触应力分布曲线图Fig.15 Curve gragh of contact stress distribution

图14和图15分析得出，圆与圆接触区的最大应力发生在中间最下端位置，接触圆弧较小；圆与椭圆接触区的最大应力也发生在中间最下端位置，接触圆弧较大；圆与椭圆接触情况下的接触应力比圆与圆接触情况下的接触应力变化更加平缓，接触区域面积更大，应力分布梯度更小，最大应力减小了54.8%。

4.3 有限元解与理论解对比分析

表3分别列出了初始模型和优化模型的理论解析解和有限元解结果，有限元解和理论解基本吻合，数据误差基本在5%左右，符合计算精度要求。两方面都验证了优化分析与设计的准确性。

表3 优化前后最大接触应力变化表/104kPaTab.3 Changes of maximum contact stress before and after optimization

5 结论

通过上述理论计算和数值分析的对比，可以得到如下几点结论：

（1）本文提出的优化设计方法，适用于轴孔连接结构中轴的受力方向为单向受力且具备对孔进行精加工而间隙能够精确控制的情况。对初始模型结构进行优化设计后，轴孔接触区的最大接触应力降低50%以上，因此本文中的优化设计方法可以用于提高轴孔连接结构承载能力的工程研究。

（2）该方法从影响轴孔接触区接触应力大小的主要因素（接触点数目及接触点处的接触曲率）出发，通过改变孔接触面的曲面形状并优化其曲面参数，使得最初接触点数目增多、接触曲率得到优化，从而使得外部载荷增加时轴孔的接触顺序从两侧逐步向中部扩展，增加了轴孔接触面的分布范围，降低了最大接触应力。

（3）与传统的连接结构设计方法相比，本方法将接触应力考虑到连接件的结构设计中，从连接件承载能力较低的根本原因出发来设计结构。利用此方法指导连接件设计，结构的利用率更高，对结构的设计工作有一定的推动作用。该设计思想也可以进一步推广应用到其他有关连接结构中，具有广泛的工程价值和应用前景。

[1]杨东升,胡伟平,吕来清.销钉耳片连接件接触应力分析的能量解法[J].应用力学学报,2011,28(3):304-307. Yang Dongsheng,Hu Weiping,Lü Laiqing.The energy approach to contact stress analysis of pinned connections[J].Chinese Journal of Applied Mechanics,2011,28(3):304-307.(in Chinese)

[2]Iyer K.Solutions for contact in pinned connections[J].International Journal of Solids and Structures,2001,38(50):9133-9148.

[3]Yavari V,Rajabi I,Daneshvar F,et al.On the stress distribution around the hole in mechanically fastened joints[J].Mechanics Research Communications,2009,36(3):373-380.

[4]颜东煌,刘雪锋,田仲初,等.销轴连接结构的接触应力分析[J].工程力学,2008,25(1):229-234. Yan Donghuang,Liu Xuefeng,Tian Zhongchu,et al.Contact stress analysis of pinned connection[J].Engineering Mechanics,2008,25(1):229-234.(in Chinese)

[5]杨生华.齿轮接触有限元分析[J].计算力学学报,2003,20(2):189-193. Yang Shenghua.Finite element analysis of gear contact[J].Chinese Journal of Computational Mechanics,2003,20(2): 189-193.(in Chinese)

[6]窦鹏,李友国,梁开明,汪长安.CVC热轧机支承辊接触应力有限元分析[J].清华大学学报,2005,45(12):1668-1671. Dou Peng,Li Youguo,Liang Kaiming,Wang Changan.Finite element analysis of contact stresses on the backup roll of CVC hot rolling mills[J].Journal of Tsinghua University,2005,45(12):1668-1671.(in Chinese)

[7]魏大盛,王延荣.榫连结构接触面几何构形对接触区应力分布的影响[J].航空动力学报,2010,25(2):407-411. Wei Dasheng,Wang Yanrong.Effects of profile of contact surfaces on the stress distribution for tenon jointing in blade disk assemblies[J].Journal of Aerospace Power,2010,25(2):407-411.(in Chinese)

[8]Johnson K L.Contact mechanics[M].Cambridge:Cambridge University Press,1987.

[9]Wriggers P,Zavarise G.Computational contact mechanics[M].John Wiley&Sons,Ltd,2002.

[10]王宝忠.飞机设计手册第10册:结构设计[M].北京:航空工业出版社,1994:328-329. Wang Baozhong.Aircraft design manual vol10-structure design[M].Beijing:Aviation Industry Press,2000:410-411.(in Chinese)

[11]Ciavarella M,Decuzzi P.The state of stress induced by the plane frictionless cylindrical contact.I.The case of elastic similarity[J].International Journal of Solids and Structures,2001,38(26):4507-4523.

[12]Ciavarella M,Decuzzi P.The state of stress induced by the plane frictionless cylindrical contact.II.The general case(elastic dissimilarity)[J].International Journal of Solids and Structures,2001,38(26):4525-4533.

[13]Sinclair G B,Cormier N G.Contact stresses in dovetail attachments:Physical modeling[J].Journal of Engineering for Gas Turbines and Power,2002,124(2):325-331.

[14]Belytschko T,Liu W K,Moran B,et al.Nonlinear finite elements for continua and structures[M].John Wiley&Sons, 2013.

Optimal design of improving the carrying capacity of shaft and hole connection structure

LIU Wen-zhang1,HE Jing-Wu2,YAN Bin1,WU Wen-wei1
(1.China Ship Scientific Research Center,Wuxi 214082,China;2.School of Aeronautic Science and Engineering,BeiHang University,Beijing 100191,China)

In order to improve the contact characteristics of shaft and hole connection structure and improve its carrying capacity,one method was proposed.For a typical bolt and lug connection structure,the contact analysis model was established.By Persson contact theory and optimization method,the surface shape and its parameters of the contact surface of shaft and hole were optimized to lower the maximum contact stress and improve its distribution gradient.For the optimized design results of contact surface,using finite element analysis,the FEA model of bolt and lug connection structure was created to calculate the contact stress and verify the optimization results.The results show that the calculated results of analytical method and finite element method are basically the same.Through optimization,the maximum stress of the contact area is reduced by more than 50 percent and the stress distribution gradient is improved significantly.So the carrying capacity of shaft and hole connection structure is increased.

shaft and hole connection structure;Persson contact theory;contact stress; structure optimization;carrying capacity

O343.3

A

10.3969/j.issn.1007-7294.2017.08.009

1007-7294（2017）08-1001-08

2017-02-25

刘文章（1987-），男，工程师，E-mail:articleliu@163.com；何景武（1961-），男，教授。