弹性垫形式的水下弹性体发射动力学分析

赵振军，王占莹，武龙龙，赵颖颖

（北京宇航系统工程研究所，北京100076）

弹性垫形式的水下弹性体发射动力学分析

赵振军，王占莹，武龙龙，赵颖颖

（北京宇航系统工程研究所，北京100076）

弹性垫会对水下运载器发射动力学产生影响，文章针对弹性垫形式，利用Lagrange方程推导了新型适配关系下的发射动力学方程，同时考虑了运载器的刚体运动、弹性变形、弹性垫变形与接触对发射过程的影响。利用文中的方法，建立了水下运载器发射动力学模型，对发射过程的载荷进行了求解，研究了弹性垫数量、刚度、位置等参数对运载器弹性振动的影响。结果表明文中方法是有效的，可用于水下运载器发射动力学分析。

水下运载器；弹性垫；耦合求解；模态叠加法

0 引言

水下运载器的发射是由装在发射装置底部的燃气动力装置产生高温高压气体，将运载器弹射出水，运载器受到复杂的流体外力作用引起横向振动响应[1-2]。在水下运载器发射时，需要安装弹性垫，在发射过程中起减振作用[3]。

国内外学者对水下发射动力学问题开展了研究。洛克西德马丁公司的Brooks和Laughlin[4]详细介绍了水下发射装置的组成、特点和设计参数。NACA Langley空间实验室的Dawson[5]研究了潜射导弹水下发射深度和初始俯仰角与出水俯仰角之间的关系。西屋电气公司的Burgdorf[6]提出了一种水下发射导弹尾空泡和横流作用下的水动力建模方法，分析了两种构型导弹水下发射过程中的姿态角变化，与试验结果对比取得了较好的一致性。

国内赵世平等[7]基于导弹运动方程研究了艇速、适配器刚度和导弹垂向运动速度等发射条件对潜载垂直发射导弹在横向流作用下的受力和出筒运动参数的影响。李代金和张宇文等[8]通过建立潜射导弹动力学模型，研究了艇速、适配器刚度等发射条件对潜载垂直发射导弹在横向流作用下的受力和出筒姿态参数的影响。以上研究主要基于刚体动力学方程，忽略了弹体弹性响应对水下发射动力学的影响。

燕国军等[9]采用Mixture多相流模型和动网格技术对航行体水下垂直发射过程进行数值模拟，研究了尾部形状和尾空泡初始压力对航行体尾部流场特征的影响。程少华等[10]基于空泡独立膨胀原理和Rayleigh-Plesset方程建立了尾空泡形态和压力的理论预示方法。张晓乐等[11]采用Lagrange结构网格和Euler流场网格耦合方法对潜射航行器出筒后筒口压力场进行了数值仿真，获得了筒口压力场气泡脉动主要特征。以上研究主要关注水下运载器的水动外力特征，未考虑弹体弹性响应对水下发射动力学的影响。

本文利用水下运载器的结构模态数据，研究了考虑运载器弹性变形影响的弹性垫形式水下发射动力学分析方法，分析了弹性垫参数对姿态和结构弯矩响应的影响。

1 水下运载器发射的力学模型

水下运载器发射系统主要包括运载器、发射筒、弹性垫和燃气动力装置。为了从数学上求解水下运载器发射问题，首先需要对运载器水下发射这一复杂物理过程进行力学简化，见图1，主要假设和简化处理如下：

（1）假设运载器在跟随其运动的坐标系中的变形可视作小变形，运载器简化为柔性梁模型，利用模态数据进行描述；

（2）忽略发射筒的变形和运动，简化为固支边界条件；

（3）弹性垫简化成非线性弹簧元件，一端固支，另一端与柔性梁存在接触关系；

（4）燃气动力装置产生的燃气作用简化成底部位移或时变的集中力；

（5）发射过程中的水动外力简化为沿弹长方向的分布力和头部的时变集中力。

图1 发射动力学模型简图Fig.1 Diagram of the underwater launching dynamic model

2 基于模态的水下运载器发射动力学方程推导

基于分析动力学理论，利用Lagrange方程[12]推导了弹性运载器的水下发射动力学方程。

为了简要说明其物理概念，现假设运载器只在一个平面内运动，如图1所示。梁上任一点t时刻的横向速度为式中：ξ表示梁上任一点的局部坐标系，qi表示第i阶模态坐标，xc和yc为跟随运载器运动的坐标系的原点，θc为随运载器运动的坐标系x轴与惯性坐标系O0x0y0z0的x0轴之间夹角，和为第i阶模态在坐标系Oxyz的x轴和y轴方向上的分量。

整个梁的动能T可以表示为：

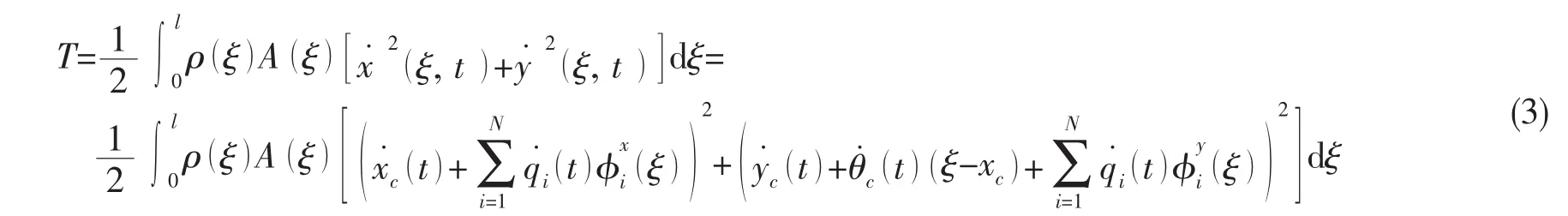
式中：ρ为梁上ξ处的密度，A为梁上ξ处的截面积，l为梁长度。

整个梁的变形能U可以表示为：

式中：E为梁上ξ处的杨氏模量，I为梁上ξ处的截面惯性矩，u为梁轴向位移，N为截取的模态数，M为弹性垫数量，Kj为第j道弹性垫的非线性刚度，用于判断第j道弹性垫是否与运载器接触，有

δj为第j道弹性垫的变形量，并且有

选取xc、yc、θc、qi（i=1,L,N）作为广义坐标。

根据第二类Lagrange方程[3]：

式中：Q为广义坐标q对应的广义力。

并利用（3）式和（4）式，得到如下方程组：

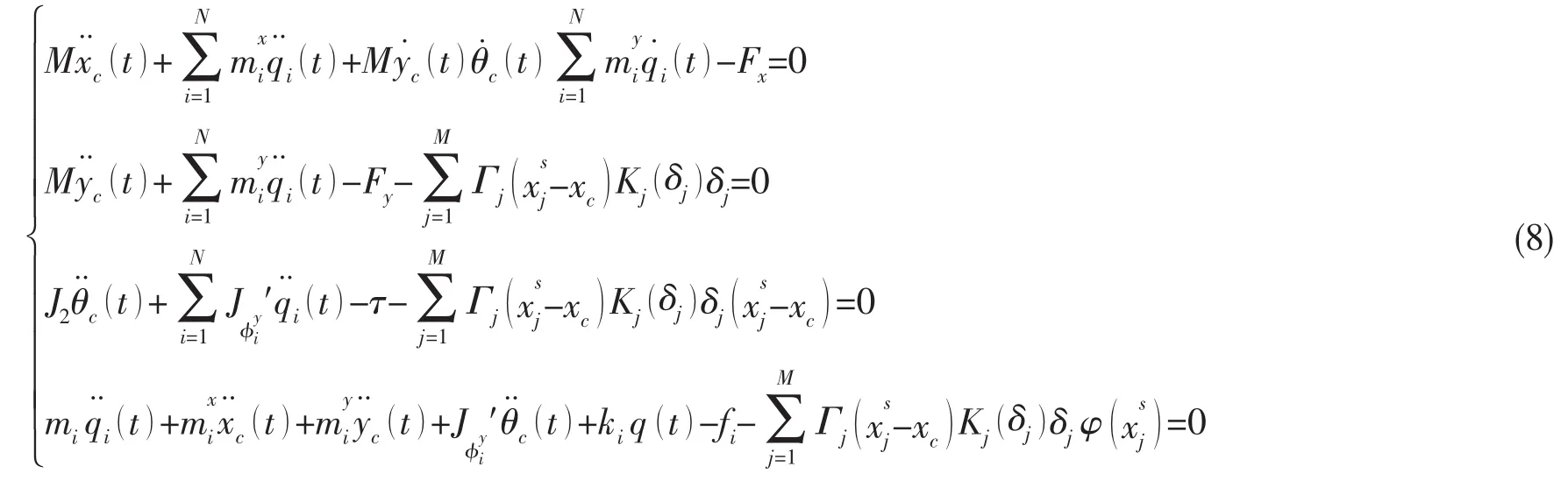
其中：

Fx和Fy为作用在梁上的合外力在惯性系O0x0y0z0的x0轴和y0轴方向上的分量，为作用在梁上的合外力矩，fi为第i阶模态坐标qi对应的广义力，考虑到小变形情况下，近似满足

方程组（8）即是运载器的刚体运动与弹性变形耦合方程，其中该方程组中的第一和第二个方程为运载器的平动方程，第三个方程为运载器的转动方程，第四个方程为运载器的弹性振动方程。

求出各振型的广义坐标qi后，利用模态弯矩，可以得到弯矩

利用给定压力分布系数下，弹体受到的横向分布水动力按下式考虑：

式中：v和α分别为弹体与水的局部相对速度、弹体局部攻角，A为弹体特征面积，△L为单元高度。

3 结果分析与讨论

3.1 建模与计算结果

针对某型水下运载器，首先利用质量和结构参数，建立有限元模型，在此基础上，进行模态分析，前两阶振型见图2和图3。

弹性垫采用非线性弹簧元件模拟，图4给出了弹性垫刚度曲线。

利用本文方法，对运载器发射动力学问题进行了求解，获得了特征面弯矩如图5实线所示，该截面出筒时刻弯矩达到最大，主要由于此时刻运载器出筒部分形成悬臂梁，而该截面正处于悬臂梁的根部。该截面出筒后，不再受到弹性垫的限制，因此产生了一定高频弹性振动。将该截面以上水动力对该截面取矩，得到该截面的合外力矩，如图5虚线所示，结果表明，在发射过程中，合外力矩基本可以包络截面弯矩，决定了截面弯矩的量级。

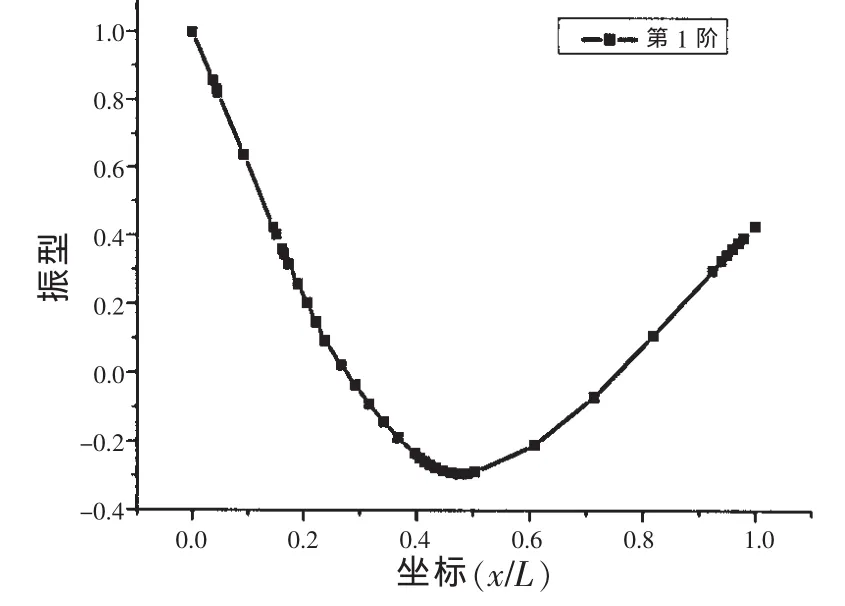
图2 第1阶振型Fig.2 The first order shape

图3 第2阶振型Fig.3 The second order shape

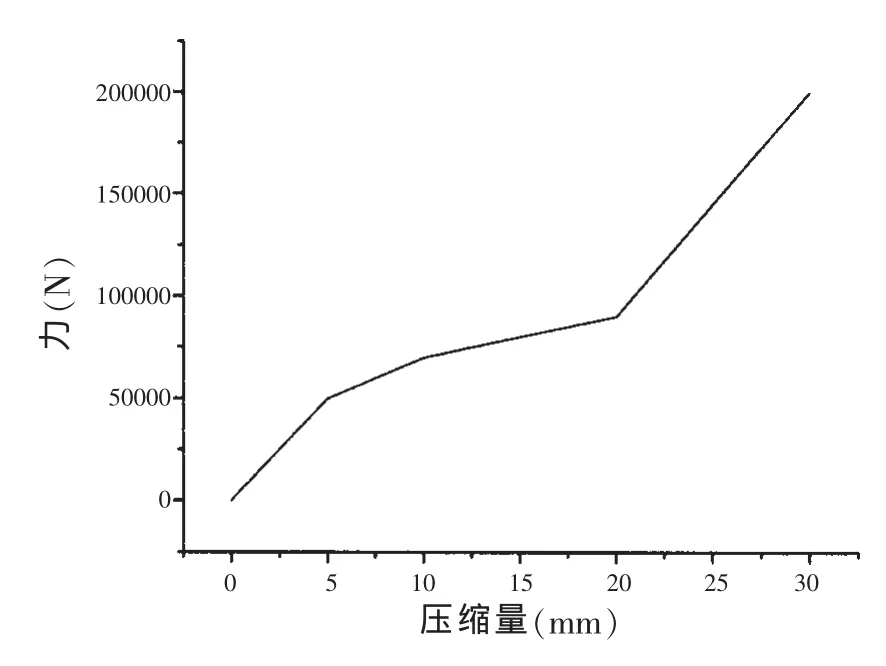
图4 弹性垫刚度曲线Fig.4 The stiffness curve of the elastic cushion

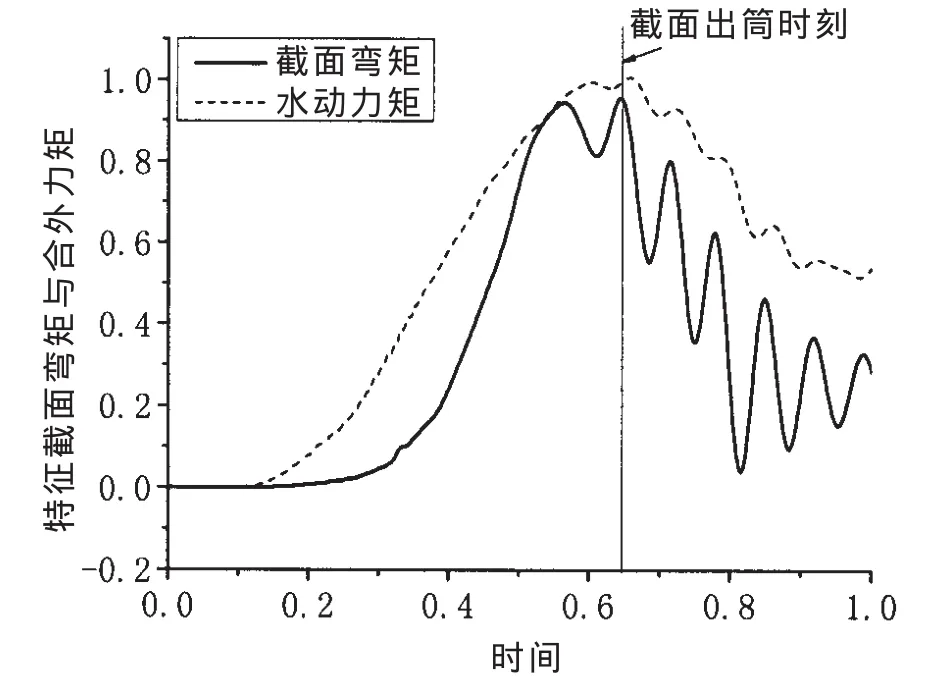
图5 特征面弯矩与水动外力矩对比Fig.5 Comparison between the bent moment and the external moment on the characteristic section

3.2 参数影响分析

利用本文方法，研究了弹性垫刚度、数量等参数对运载器弹性振动的影响。

3.2.1 弹性垫整体刚度的影响

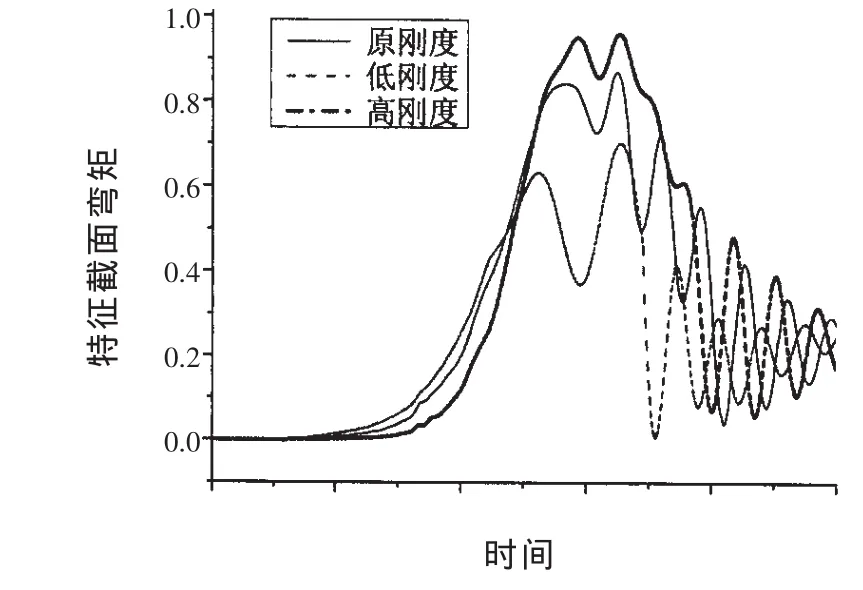
图6 不同刚度下的特征截面弯矩响应Fig.6 The bend moment response of differential stiffness

图7 不同刚度下的弹性垫最大压缩量Fig.7 The elastic cushion maximum deformation of differential stiffness

考虑不同弹性垫刚度，利用本文方法对运载器发射过程进行计算，见图6～7，结果表明，由于水下运载器发射系统是非线性系统，所以刚度对截面弯矩的影响较为复杂，整体上来看，刚度越大，载荷量级越大，弹性垫压缩量越小。

从能量的观点来看，刚度较小时，弹性垫变形较大，即运载器的横向位移较大，更多的外力做功转化为运载器动能，从而转化为变形能的部分减少，弯矩量级相对较小。从达朗贝尔原理来讲，运载器的横向位移较大，说明惯性响应较大，惯性力矩抵消了一部分外力矩，量级相对较小。但在实际工程设计中，还需要考虑最大允许变形量和姿态角等限制条件，因此弹性垫刚度的选择需要综合考虑各种因素。

3.2.2 弹性垫数量的影响

考虑不同弹性垫数量，对运载器发射过程进行计算，见图8，结果表明：随着弹性垫数量减少，载荷的脉动部分增大，增加弹性垫数量可以使运载器发射过程更为平缓，降低由于弹性垫边界条件变化引起的惯性响应。

图8 不同弹性垫数量下的特征截面弯矩响应Fig.8 The bend moment response of differential cushion count

4 结论

本文利用Lagrange方程推导了运载器发射动力学方程，实现了运载器发射过程的运动和载荷的耦合求解，主要结论如下：

（1）本文方法考虑了运载器的刚体运动、弹性变形、弹性垫变形与接触对发射过程的影响，可用于水下运载器发射动力学分析。

（2）在发射过程中，截面弯矩主要由水动力矩决定。

（3）弹性垫刚度、刚度分布均会对发射过程产生一定影响，从整体上来看，刚度越大，载荷脉动部分越大，弹性垫压缩量越小。

（4）弹性垫数量也会对发射过程产生影响，增加弹性垫数量可以使运载器发射过程更为平缓，降低由于接触变化引起的惯性响应。

[1]权晓波,李岩,魏海鹏,吕海波,辛万青,鲁传敬.航行体出水过程空泡溃灭特性研究[J].船舶力学,2008,12(4): 545-549. Qüan Xiaobo,Li Yan,Wei Haipeng,Lü Haibo,Xin Wanqing,Lu Chuanjing.Cavitation collapse characteristic research in the out-of-water progress of underwater vehicles[J].Journal of Ship Mechanics,2008,12(4):545-549.

[2]权晓波,燕国军,李岩,孔德才,李明.水下航行体垂直发射尾空泡生成演化过程三维数值研究[J].船舶力学, 2014,18(7):739-745. Qüan Xiaobo,Yan Guojun,Li Yan,Kong Decai,Li Ming.Three-dimensional numerical study on the evolution process of tail bubble of underwater vehicle vertical launching[J].Journal of Ship Mechanics,2014,18(7):739-745.

[3]黄寿康.流体动力·弹道·载荷·环境[M].北京:宇航出版社,1991.

[4]Laughlin J P,Brooks W B.Adaption of the army tactical missile system to undersea operations[J].Adaption of the Army Tactical Missile System to Undersea Operations,1996.

[5]Dawson J R.Hydrodynamic characteristics of missiles launched under water[J].Technical Report Archive&Image Library,1958.

[6]Burgdorf O.Hydrodynamics of unsteady underwater-launched missiles with trailing cavities and crossflow drag[R].AIAA paper 87-1319,Jun.1987.

[7]赵世平,蔡体敏.横向流对潜艇垂直发射导弹的影响[J].船舶力学,2006,10(4):33-37. Zhao Shiping,Cai Timin.Effects of lateral flow to the missile vertical launched from a submarine[J].Journal of Ship Mechanics,2006,10(4):33-37.

[8]李代金,张宇文,党建军,罗凯.潜艇垂射导弹出筒姿态的研究[J].弹箭与制导学报,2009(4):171-173+178. Li Daijin,Zhang Yüwen,Dang Jianjun,Luo Kai.Numerical solution for outlet attitude of the missile vertical launched from a submarine[J].Journal of Projectiles Rockets,Missiles and Guidance,2009,29(4):171-173+178.

[9]燕国军,阎君,权晓波,魏海鹏.水下航行体垂直发射尾部流场数值计算[J].导弹与航天运载技术,2012(3):42-46. Yan Guojun,Yan Jun,Qüan Xiaobo.Numerical study on tail flow field of underwater vehicle in vertical launching[J]. Missiles and Space Vehicles,2012(3):42-46.

[10]程少华,权晓波,王占莹,郭百森,尤天庆.水下航行体垂直发射尾部空泡形态与压力预示方法研究[J].水动力学研究与进展A辑,2015(3):299-305. Cheng Shaohua,Qüan Xiaobo,Wang Zhanyin,Guo Baisen,You Tianqin.Prediction method on trailing cavity shape and pressure of the underwater vehicle in vertical launching[J].Journal of Hydrodynamics,2015(3):299-305.

[11]张晓乐,卢丙举,胡仁海,杨兴林.水下航行体垂直发射筒口压力场L/E耦合数值模拟[J].舰船科学技术,2016(11): 151-155. Zhang Xiaole,Lu Bingjü,Hu Renhai,Yang Xinglin.L/E coupling numerical simulation of pressure field near launch canister outlet for underwater vehicle vertical launch[J].Ship Science and Technology,2016(11):151-155.

[12]陈滨.分析动力学[M].北京:北京大学出版社,1987.

[13]尹云玉.固体火箭载荷设计基础[M].北京:中国宇航出版社,2007.

Launching dynamic analysis on underwater elastic vehicle in elastic cushion

ZHAO Zhen-jun,WANG Zhan-ying,WU Long-long,ZHAO Ying-ying
(Beijing Institute of Space System Engineering,Beijing 100076,China)

The elastic cushion design has important impact on the launching dynamics of the underwater flexible vehicle.In this paper,the launching dynamic equation of new adaptation pattern is derived for the elastic cushion launching system by using Lagrange’s equations,in which the impact of the rigid-body motion,elastic deformation,deformation and contact of elastic cushion on the launching dynamics are considered.The presented method is used to create the the launching dynamic model,and analyse the dynamic response of structural load,study the impact of the design parameter of elastic cushion on the launched flexible vihicle.The results show that the presented method is effective in the launching dynamic analysis of the underwater flexible vehicle.

underwater flexible vehicle;elastic cushion;coupled solution;mode superposition method

O303O352

A

10.3969/j.issn.1007-7294.2017.08.006

1007-7294（2017）08-0976-07

2017-01-03

国防973项目（6131140201，6131770304，6132770102）

赵振军（1979-），男，博士，高级工程师，E-mail:zhaozhenjunzzj@163.com；王占莹（1983-），女，硕士，高级工程师。