基于CFD流固耦合理论的海上浮式结构物水动力性能分析
马哲,程勇,翟钢军
(1.大连理工大学深海工程研究中心,辽宁大连116024;2.江苏科技大学船舶与海洋工程学院,江苏镇江212003)
基于CFD流固耦合理论的海上浮式结构物水动力性能分析
马哲1,程勇2,翟钢军1
(1.大连理工大学深海工程研究中心,辽宁大连116024;2.江苏科技大学船舶与海洋工程学院,江苏镇江212003)
文章利用流体动力学控制方程和结构运动方程的耦合理论,在具有造消波功能的2D数值水槽中实现了海上浮式结构物在波浪中运动过程的数值模拟。以系泊式浮式方箱防波堤作为工程应用实例,分别采用梯形法和二、三阶单步数值迭代法对浮体的动力特性进行数值分析,并与基于势流理论的边界元法的结果做对比,分析后发现在波浪条件下梯形法和二、三阶单步法的计算精度相当,结果收敛,且与边界元法结果吻合较好,满足要求。该文提出了一种新的全自由度分块结构移动网格技术,实现了浮体所有方向的联合运动,而且网格不发生任何扭曲现象,计算时间、网格划分和精度要求都得到了较好的控制。
流固“全耦合”;梯形法;二、三阶单步法;全自由度分块结构移动网格技术
0 引言
在海洋工程领域,海洋平台、船舶和FPSO等海洋结构物在波浪作用下经常会发生波浪运动、砰击和甲板上浪等现象。为了保证海洋结构物在自存和工作工况下的安全性,因此对各种水动力现象进行特性分析起着至关重要的作用。在计算流体动力学中,研究此问题的方法大致可分为两类:一类是根据势流理论,首先预报出结构在波浪作用下的运动规律,然后规定结构按照此规律运动,从而实现结构的运动和流场变化,其中对于结构运动采用移动网格技术实现。林兆伟,朱仁传等学者[1]在一个具有造消波功能的二维数值水槽中提出多层动静网格匹配方法,研究了甲板上浪问题;郭海强[2]采用动计算域和滑移网格匹配法计算了船体剖面运动的水动力系数;龚丞[3]等结合势流理论与CFD的优势,模拟分析了甲板上浪现象及其对甲板结构的冲击作用,船体运动规律由势流理论确定,然后通过FLUENT软件进行船舶的甲板上浪模拟。另一类是根据流体和浮体的耦合作用,首先算出流体对浮体的作用力,然后根据浮体的运动方程算出浮体的速度和位置,浮体的速度和位置可以改变周围的流场,即浮体和流体之间是相互耦合的。Hadzic,Henning[4]等学者基于Reynolds平均化的Navier-Stokes(N-S)方程和刚体运动方程的耦合迭代求解法,采用网格的变形和滑移技术预测浮体在波流作用下的运动规律;Nielsen[5]等基于Navier-Stokes方程,采用VOF自由液面捕捉法研究了FPSO在波浪作用下的甲板上浪问题;Yang和Qiu[6]等基于CIP(Constrained Interpolation Profile)的有限差分法求解N-S方程计算二维及三维物体的波浪抨击力,其中流体压力采用共轭梯度迭代法(conjugate gradient iterative method)求解泊松型方程得到;Kleefsman[7]等基于不可压缩粘性流体的N-S方程研究了由波浪抨击力引起的溃坝及物体入水问题,详细阐述了在固定笛卡尔坐标系下基于有限体积法的N-S方程离散方法,并对溃坝及楔体入水实验进行了数值仿真模拟;Shen和Yang[8]等通过实验及FLUENT软件研究了聚焦波浪作用下风机基础的波浪荷载问题。
对于预先知道浮体运动形式的水动力求解问题,由于运动规律根据势流理论分析得出,流体作用在湿表面上的压力和剪应力不会改变浮体的速度和位置,因此这种方法不是真正意义上的流体和浮体的耦合模拟,而是一种“半耦合”数值模拟技术,此方法明显的缺点是不能模拟出浮体的漂移效果。在数值造消波的水槽中研究浮体的运动和受力,最理想的途径是“全耦合”数值方法,但由于此方法计算量大,对动网格的质量和数值计算精度要求高,因此到目前为止研究甚少。本文采用流体动力学控制方程和浮体运动方程的耦合技术,在2D数值造消波水槽中实现了对浮体运动和受力等水动力性能的研究。其中对浮体的运动规律求解分别采用了梯形法和二、三阶单步法,并使用VOF法追踪自由液面来模拟浮体对流场的耦合作用,浮体所有方向的联合运动通过一种新的全自由度分块动静结构网格和平动、旋转滑移交界面技术实现。
海洋工程结构物在流场中的CFD数值模拟,普遍采用移动网格的方法,其实现形式主要有5种:一是伴随着物体的运动,移动整个计算域的网格,随之自由面位置不断变化,因此需要指定外域的边界条件。此方法只适用于浮体在无限域中的运动;二是紧贴物体周围的网格与物体一起做刚体运动,较远部分采用固定网格,这两个域之间的调整区采用变形网格。此方法的优点是易于指定外域边界条件,而缺点是只能考虑浮体单一方向的平动,且在调整区的网格变行和扭曲不能过大,即浮体的运动必须是微小幅值的;三是把方法二中的调整域改成重构网格域,此方法的优点是可以应用于任意浮体运动,不足是需采用非结构网格进行网格划分和重构,且必须保证相当的精度,新的重构网格还采用原来的求解插值方法,易引入额外的误差;四是动计算域和滑移交界面的联合使用,物体周围的随体网格和物体一起做刚体运动,考虑到浮体的旋转运动,这个域的边界划分为圆形或者球形,外部网格做压条运动。此方法能很好的保证网格质量,但它对网格的划分要求较高;五是采用重叠网格技术,浮体周围的随体网格与浮体一起做刚体运动无变形,外部网格采用固定网格,两个网格域在浮体附近重叠,这样浮体可以无限制的运动,且利于考虑多体运动,但对于非结构网格,在重叠区域的网格耦合和保持守恒特征有一定困难。本文在方法四的基础上进行改进,将整个计算域由里向外分成4层,所有网格均为结构网格,第一层随体网格是圆域,可随浮体一起做任意方向平动和转动的联合运动,第二层是过渡域,只做平动,第三层为矩形网格域,只做平动,第四层为静止网格域(如果外域边界为动边界条件,则可以有网格运动,如:造波板边界条件)。此动网格技术中采用三组交界面,一为圆周边界的滑移交界面,方便随体网格做旋转运动;二为小矩形交界面,用于实现两域网格流场信息的过渡;三为动网格域与静网格域的滑移交界面,其中内交界面随动网格做平动。
1 数学模型
1.1 流体运动控制方程
本文采用VOF法捕捉自由液面,根据网格单元内流体所占体积分数来追踪自由液面的变化过程。这种方法的优点在于可以跟踪翻转、吞并、破碎、上浪、冲击等复杂的非线性自由面现象。
在本文的研究中,计算域包含空气和水两种介质,流体为不可压缩的,忽略粘性,则流场控制方程为:

式中:u,y分别为x,y方向的速度;ρ为流体密度;p为流体压强;g为重力加速度;aq为第q相流体单元内所占的体积分数,q=1,2分别代表空气和水。
1.2 配有锚链系泊的浮式防波堤计算模型
为了研究浮体在波浪中的运动和受力,本文对锚链系泊的浮式防波堤进行数值模拟。假设锚链对称布置,初始为自然伸长状态,导缆孔位于防波堤两角点,且只承受拉力,应力应变服从胡克定律,锚链刚度466.0 N/m,忽略其质量、阻尼的影响和浮体转动引起的转动惯量变化。规定所有变量垂直向上和水平向右为正,弯矩逆时针为正,以浮式方箱防波堤为例进行受力分析。在波浪作用下,防波堤受到重力、流体作用力和锚链力,对防波堤建立运动方程如下:

式中:x,y分别为防波堤x和y方向上的位移;θ为防波堤的转角;fx,fy分别为防波堤所受流体作用力在x和y方向上的分量,通过联立(1)、(2)式和(3)式求出的流体压力沿浮体湿表面积分获得;I为防波堤绕重心的转动惯量,Mfg为流体作用力对防波堤重心的力矩,根据湿表面每个单元x和y方向上的流体作用力所产生的力矩沿湿表面积分计算出;Fx锚链、Fy锚链分别为x和y方向上的锚链力,表示为:


Mx和My分别为x和y方向上的锚链力对防波堤重心的力矩,当x≥0,y≥0时:

这里Y为导缆孔y方向坐标;Y_cg为重心纵坐标;k为锚链刚度;X_left,Y_left,X_right,Y_right,X_cg,Y_cg分别为左右角点及重心的全局坐标。由以上分析得,联立(1)~(7)式可求解浮式防波堤所受的流体作用力、运动速度、位置及锚链力。
2 数值计算方法
2.1 造消波技术
根据推板造波理论[9],冲程为X0,圆频率为ω,平衡位置在原点的造波机做简谐运动的水平速度为:

在水深为d的2D水槽中,产生的波面高程为:

式中:η( x,t)为波面的瞬时高程;k为规则波的波数,由色散方程ω2=gktanh( kd)得出;ki(i=1,2…,n)由色散方程ω2=-gktan( kd)得出。等号右边的第1项为造波板运动产生的传递波,第2项为造波板运动产生的局部振荡,随距造波板距离增大呈指数衰减,达到一定距离后可忽略不计,因此需设置前端缓冲区来过滤掉非传播模态,得到所需的规则波波面。
为保证计算的稳定性,造波板的运动规律采用如下形式:

根据王本龙和宋帅[10-11]等的阻尼海绵层消波理论进行数值消波,即在数值水槽的消波区设置海绵层来吸收穿过工作区的能量,使速度场和压力场逐渐衰减,水槽边界处几乎无波浪反射,以消除反射波对工作区的影响,从而保证数值水槽模拟的准确性。消波区的速度和压强分别为:

式中:下标C表示在进入海绵层之前的波动场;下标M表示修正后的波动场;λ=λ(x)为与空间位置有关的从0~1之间的光滑过渡加权函数。本文取:

式中:x1为消波区左端点的横坐标,xl为海绵层长度。
2.2 梯形法和二、三阶单步数值计算方法
一阶常微分方程初值问题的梯形数值解法和二、三阶单步法分别具有二阶和四阶精度,本文分别采用这两种方法进行时间推进,并作比较分析。
设一阶常微分方程初值问题为

梯形法的求解公式为:

二、三阶单步求解公式同时包含二阶和三阶两个单步公式,比单独使用二阶或三阶单步法具有更高的准确性。该方法的计算分为三个阶段,需求四个斜率ki(i=1,2,3,4)。k1的初始值可由t0,u0计算得到,以后每积分一步,将k4作为下一时间步k1。该算法的关键步骤如下:

其中:u0表示初始时刻a的值;tn=tn-1+h;un,un-1分别表示此刻和积分前一步时刻的函数值;h表示时间步长。在时间步长h中,将前一时间步的x、y方向上的位移x0,y0,角点和重心位置作为锚链力和弯矩计算的初值带入等式右边,算出这一时刻的位移x1,y1和坐标,设定目标精度为ε,则当且时认为收敛,停止计算,否则将此刻位移x1,y1和坐标赋给x0,y0和初始坐标代入等式右边重复上述步骤,直到满足精度要求为止。
在计算中,将浮式防波堤的运动方程(5)、(6)和(7)改写成具有初值问题的一阶常微分方程组,即:

式中:u,v,ω1分别为浮式防波堤的水平,垂直方向的线速度和角速度,数值迭代计算时,初值都设置为0。
2.3 全自由度分块结构移动网格技术
目前运用移动网格方法实现流场中运动浮体数值模拟的CFD技术中,多数学者采取的是将纵荡、垂荡和纵摇(2D数值模拟)分别处理或将纵荡、垂荡两者之一与纵摇一起联合处理。网格都可划分为结构网格,计算精度高,但却无法考虑所有自由度运动的相互耦合影响。有人提出在随体圆形区域网格的外围设置非结构三角形网格,通过刚体运动和网格重构的方法模拟浮体上述三种方式的联合运动,但网格再生耗费时间长,分辨率不易控制,而且再生网格局部可能产生过大的扭曲度或网格形状发生突变,引起收敛困难和精度降低。
本文采取全自由度分块结构移动网格技术,实现2D数值水槽中运动浮体纵荡、垂荡和纵摇所有方向上的联合运动,数值模拟时,浮式防波堤置于水槽工作区中央,重心在静水面以下0.4 m处,如图1所示。工作区的动静网格细划分情况如图2所示。定义围绕浮式防波堤的圆域3为刚体网格,既有平动又有转动,网格尺度与扭曲度均不变,且与物体的相对位置不变;结构平动网格域2只有平动,网格尺度与扭曲度不变;结构平动网格域1采用动态网格层变法实现网格的平动变形,且保持扭曲度不变。这里三个移动网格域均采用结构网格,其中域1采用矩形结构网格。在设置边界条件时,域1与工作静止区,域1与2以及圆域3与域2分别设置一对interface,以保证运动时各个子区域互不干扰,同时相邻区域的流场信息通过插值方式实现相互传递。此外,定义域1的左右边界做垂向运动,同域1的垂向速度,而上下边界做水平运动,同域1的水平速度,来实现防波堤纵荡、垂荡和纵摇三种方式的联合运动。
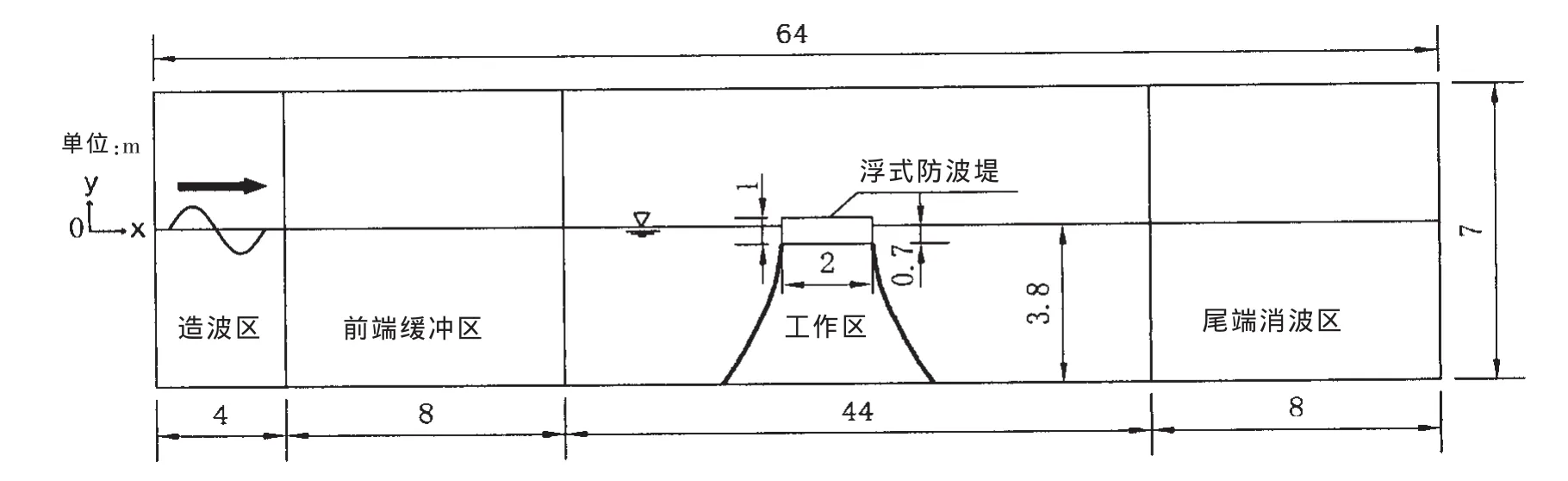
图1 2D数值水槽示意图Fig.1 The sketch of 2D numerical tank

图2 结构移动网格的分块划分Fig.2 Meshing of multiply structured grids
3 数值试验与结果分析
按以下要求划分计算域网格以保证数值模拟的精度:波浪传播方向上的网格数量必须充足,以避免数值阻尼引起入射波浪衰减;造波区、前端缓冲区和工作区水平网格尺寸约为波长的1%,尾端消波区可适当增大,这样既可减少计算时间,又可配合阻尼海绵达到更好的消波目的;为精确捕捉自由面的变化过程,垂直方向的网格在自由面附近约5%波高,距离越远网格尺寸越大;精细划分浮体附近的网格,可更好地模拟物体和流体之间的相互耦合作用。
3.1 数值造消波的验证
为验证数值水槽的造消波效果,本文按比例尺1: 10模拟波高为0.4 m,周期2.21 s(波长7.62 m)的2D行进波。根据Ursell和Dean[12]的线性造波机理论,计算得出冲程X0=0.205。x=2 m、22 m、62 m处的波面时间历程,如图3所示。由图中可测得三处波高分别为0.45 m,0.39 m,0.001 4 m,周期约2.20 s。在x=2 m处,造波区内的波浪包含传播模态和非传播模态,尚未完全衰减,故波高偏大;在x=22 m处,工作区内的传播模态已基本衰减,因此模拟波高近似理论值;在x=62 m处,消波区内的波面经过阻尼海绵已基本消减,因此近似静水面,消浪效果良好。
3.2 全自由度分块结构移动网格技术的验证
本文通过基于流固“全耦合”原理的全自由度分块结构移动网格技术分别采用梯形法和二、三阶单步法进行比较和验证,这里以一浮式方箱防波堤为例,模型尺寸和环境要素如前所述。浮式方箱防波堤在静水中浮力等于和小于重力时,垂荡速度和流体垂向作用力的时间历程曲线如图4~5所示。其中图5所示的防波堤质量为1.787e3 kg。由图4(a)可见,采用梯形法和二、三阶单步法计算得到的浮体垂荡速度随时间变化趋势相同,但二、三阶单步法的曲线较梯形法更加光滑均匀,二者随着时间的推进,都逐渐衰减趋于零,这是由于初始阶段流体和空气存在相对压强使得浮力略小于重力,浮体做微小幅值的垂荡运动。由图4(b)可见,由于初始阶段流体和空气存在密度差,使得流体垂向作用力为13 654.70 N,与重力差值为13 704.57-13 654.70=49.87 N,因此防波堤所受的流体垂向作用力大致以浮力13 654.70为中心线做上下振荡,两种方法对应的曲线变化趋势基本相同,但与梯形法相比,二三阶单步法的振动幅值略微偏小,可见二、三阶单步法的数值模拟更加精确。由图5(a)可见,当浮力小于重力时,浮式方箱防波堤做垂向往复衰减运动,两种方法对应的浮体垂荡速度几乎完全重合。由图5(b)中可见,初始阶段由于浮力小于重力,浮式方箱防波堤垂直向下运动,随着浮体吃水增加,浮力也随之增加,运动由变加速到变减速再到变加速,如此循环下去,最终流体垂向作用力大致以重力17 530.47 N为中心线做衰减简谐运动。图中两条曲线趋势大致相同,二、三阶单步数值迭代方法光滑度略高于梯形法。从图4和图5的浮式防波堤水动力性能分析,可以看出本文的流固全“耦合”方法和全自由度分块结构移动网格技术算法稳定,收敛良好,精度满足要求,与工程实际情况相符,且二、三阶单步数值迭代法的数值结果要更加均匀和光滑。

图3 不同位置的波面时间历程Fig.3 Time series of wave profile at x=2 m,22 m,62 m

图4 浮式方箱防波堤在静水中浮力等于重力时的垂荡速度和流体作用力Fig.4 Heaving velocity of the floating breakwater and fluid force when buoyancy force is equal to force of gravity in still water

图5 浮式方箱防波堤在静水中浮力小于重力时的垂荡速度和流体作用力Fig.5 Heaving velocity of the floating breakwater and fluid force when buoyancy force is less than force of gravity in still water
3.3 系泊式浮式方箱防波堤在波浪条件下的水动力特性分析
为了研究系泊式海上建筑物在波浪作用下的动力过程,这里对近年来海洋中日益增多锚链系泊的浮式方箱防波堤运动过程进行数值模拟,关于模型参数和海况条件如前文所述。图6分别描述了规则波中,系泊式方箱防波堤的运动速度,所受锚链力(矩)和流体作用力(矩)(均以无因次量表示)。其中为进一步验证基于“全耦合”方法所采用的全自由度分块结构移动网格技术对实现结构所有方向上运动的准确性,本文将数值计算所得的防波堤速度和锚链力分别与基于势流理论的边界元法所得结果进行比较。由图6(a)可见,本文数值方法与边界元法所得结果吻合较好,且在三个方向上梯形法与二、三阶单步法计算出的浮式防波堤的速度基本相同。其中水平方向和垂直方向上的线速度均只呈现出波频约2.86 rad/s的振荡特性,而绕重心的角速度的时程曲线则呈现出波频约为2.86 rad/s和低频约为0.348 rad/s相结合的振荡特性,可见纵荡和垂荡运动主要受行进波的影响,而纵摇运动与行进波和浮体固有特性两者都有关。由图6(b)可见,对锚链力的计算,本文“全耦合”方法与边界元法所得结果除了峰值和谷值略有差别,其他都吻合较好。随波浪稳定传播,防波堤在水平方向、垂直方向和纵摇方向受到的锚链力(矩)都以波频约2.86 rad/s做振荡运动,且梯形法和二、三阶单步法结果基本相同。由图6(c)可见,防波堤水平方向上和绕重心的流体作用力(矩)大致分别以-0.05和0为平衡点做有规律的往复波频振动,且波谷的绝对值要大于波峰,其与波浪的传播方向所引起的漂移运动有关;防波堤垂直方向上所受的流体作用力大致以1.94(约为14 438 N)为中心线做往复波频振动,此中心线14 438 N略大于防波堤静水平衡时所受的浮力13 704 N,这是因为锚链线对防波堤的垂直向下的作用使得防波堤下沉,浮力也随之增加,由图可知梯形法与二、三阶单步法的曲线趋势基本一致。


图6 波浪中防波堤的运动速度、锚链力和流体作用力的时间历程Fig.6 Velocity component,mooring forces and fluid force of floating breakwater in wave
4 结语
本文采用耦合求解流体动力学控制方程和浮式结构运动方程的方法,在具有数值造消波功能的2D数值水槽中,实现了海上浮式结构物在波浪中运动过程的数值模拟。以配有锚链系泊系统的浮式方箱防波堤作为算例,研究了浮式防波堤的水动力性能。在数值计算中,采用梯形法和二、三阶单步数值迭代法进行浮体运动参数的时间推进,并且采用全自由度分块结构移动网格技术,实现了浮体所有方向的联合运动,从而保证了在计算过程中网格不发生任何扭曲现象,计算时间、网格划分和精度要求都得到了较好的控制。主要得出以下结论:
(1)对静水中自由漂浮的浮式方箱防波堤,当浮力分别等于和小于重力时,用梯形法和二、三阶单步数值迭代法计算得浮体水动力特性变化趋势基本一致,结果收敛,但二、三阶单步法得出的结果较梯形法更加平顺、光滑,从而验证了流固耦合方法和全自由度分块结构移动网格技术的可行性。
(2)建立2D数值波浪水槽,根据推板造波理论在水槽中模拟规则波浪,经验证工作区的波浪条件满足理论值的精度要求,且消波区的数值海绵层消浪效果较为理想。
(3)在已建的波浪水槽工作区中央放入系泊式浮式方箱防波堤模型,采用本文数值方法对其水动力特性进行分析,并将结果与基于势流理论的边界元法进行比较。防波堤的纵荡和垂荡运动主要为波频运动,而纵摇运动为波频运动和与防波堤固有低频特性相关的低频运动相结合的运动方式,在波浪中所受的锚链力(矩)的时程曲线均表现为波频振荡趋势,且结果与边界元分析所得吻合较好。
(4)系泊式浮式方箱防波堤在波浪作用条件下,水平方向上和绕重心的流体作用力(矩)大致分别以-0.05和0为平衡点做有规律的往复波频振动,且波谷的绝对值要大于波峰,其与波浪在传播方向所引起的漂移运动有关;垂直方向上的流体作用力的中心线值比静水平衡条件下浮体所受的浮力略大,原因是锚链对防波堤的垂向作用使得防波堤下沉,浮力也随之增加。
(5)二、三阶单步求解公式在数值原理上比单个使用二阶或三阶单步法具有更高的准确性,这一点也在静水条件下浮体的运动中得到验证,但在波浪中它与梯形法的计算结果基本一致,数值收敛情况和精度也基本相同,因此防波堤的动力特性运用梯形法计算即可。
以上计算结果表明,本文采用的流固耦合方法和移动网格技术可以用来分析一系列海上浮式结构物在波浪条件下的水动力问题,但在数值模拟系泊系统时做了一些假定,并且未考虑锚链和浮体的耦合作用以及锚链对流场的影响。因此,如何更加精确、更加全面地计算结构在波浪中的动力问题还有待于进一步研究。
[1]林兆伟,朱仁传,缪国平.甲板上浪问题的二维数值模拟[J].船舶力学,2009,13(1):1-8. Lin Z W,Zhu R C,Miao G P.2-D Numerical simulation for green water on oscillating ships[J].Journal of Ship Mechanics,2009,13(1):1-8.
[2]郭海强.船舶性能数值水池的研究及其若干应用[D].上海:上海交通大学船舶海洋与建筑工程学院,2009. Guo H Q.The development and some applications of ship performance numerical tank[D].Master thesis,Shanghai Jiao Tong University,School of Naval Architecture,Ocean and Civil Engineering,Shanghai,2009.
[3]龚丞,朱仁传,缪国平,范菊.基于CFD的高速船甲板上浪载荷的工程计算方法[J].船舶力学,2014,18(5):524-531. Gong C,Zhu R C,Miao G P,Fan J.A numerical method of the simulation of green water on the deck of a vessel[J].Journal of Ship Mechanics,2014,18(5):524-531.
[4]Hadzic I,Hennig J,Peric M,Xing-Kaeding Y.Computation of flow-induced motion of floating bodies[J].Applied Mathematical Modelling,2005,29:1196-1210.
[5]Nielsen K B,Stefan M.Numerical prediction of green water incidents[J].Ocean Engineering,2004,31(3-4):363-399.
[6]Yang Q Y,Qiu W.Numerical simulation of water impact for 2D and 3D bodies[J].Ocean Engineering,2012,43:82-89.
[7]Kleefsman K M T,Fekken G,Veldman A E P,et al.A Volume-of-Fluid based simulation method for wave impact problems[J].Journal of Computational Physics,2005,206(1):363-393.
[8]沈玉稿,杨建民,李欣,等.风机基础所受波浪抨击力的数值模拟和实验研究(英文)[J].船舶力学,2013,17(9): 1009-1020. Shen Y G,Yang J M,Li X,Peng T.Numerical and experimental investigations of the impact force on offshore wind turbine pile[J].Journal of Ship Mechanics,2013,17(9):1009-1020.
[9]王文华,王言英.圆柱在波浪中入水的数值模拟[J].上海交通大学学报,2010,44(10):1393-1399. Wang W H,Wang Y Y.Numerical study on cylinder entering water in wave[J].Journal of Shanghai Jiaotong University, 2010,44(10):1393-1399.
[10]王本龙,刘桦.一种适用于非均匀地形的高阶Boussinesq水波模型[J].应用数学和力学,2005,26(6):714-722. Wang B L,Liu H.Higher order boussinesq-type equations for water waves on uneven bottom[J].Applied Mathematics and Mechanics,2005,26(6):714-722.
[11]宋帅,尤云祥,魏岗.孤立波与直墙式多孔介质结构相互作用数值分析[J].海洋工程,2007,25(4):7-14. Song S,You Y X,Wei G.The interaction of the solitary wave with a vertically walled porous structure[J].Ocean Engineering,2007,25(4):7-14.
[12]Ursell F,Dean R G,Yu Ys.Forced small-amplitude water waves:a comparison of theory and experiment[J].Fluid Mechanics,1960,7(Pt1):33-52.
[13]FLUENT INC.Fluent 6.2 Manual[M].Fluent Inc.,2004.
[14]王福军.计算流体动力学分析[M].北京:清华大学,2004. Wang F J.Computational Fluid Dynamics Analysis[M].Beijing:Tsinghua University,2004.
[15]施吉林,张宏伟,金光日.计算机科学计算[M].北京:高等教育出版社,2005. Shi J L,Zhang H W,Jin G R.Computer Science Computing[M].Beijing:Higher Education Press,2005.
Hydrodynamic performance of the floating body based on CFD fluid-body interaction theory
MA Zhe1,CHENG Yong2,ZHAI Gang-jun1
(1.Deepwater Engineering Research Center,Dalian University of Technology,Dalian 116024,China;2.Ship and Ocean Engineering School,Jiangsu University of Science and Technology,Zhenjiang 212003,China)
Using fluid-body interaction mechanics,the motion proceeds of a floating body was numerically simulated in regular wave,which was implemented in a wave making and absorbing numerical flume.As the application case of a box-type floating breakwater with mooring systems,dynamic characteristics of the floating body among the trapezoid,2,3order single step method and BEM based on potential flow theory were compared.The results indicate that the trapezoid and 2,3order single step method which were in good agreement with the BEM results has prospective accuracy and convergence in regular wave.This paper proposed an new technique of dynamic mesh with full 2D-3 degrees of freedom multiply structured grids, which realized the joint movement of all directions,and made sure that grids had not any distortion.The computation time,precision and meshing remained fairly well-contained.
fluid-body perfectly coupling;trapezoid;2,3order single step method; dynamic mesh with full freedom multiply structured grids
TV131.2
A
10.3969/j.issn.1007-7294.2017.08.003
1007-7294(2017)08-0950-10
2016-12-22
国家自然科学基金应急管理项目(51651902);国家自然科学基金青年基金项目(51609109);中央高校基本科研业务费(DUT16QY22);江苏省自然科学青年基金(BK20160556)
马哲(1983-),男,博士,E-mail:deep_mzh@dlut.edu.cn;程勇(1986-),男,博士。

