基于信噪比排序的MIMO-OFDM信号检测方法
郑建宏,李玉菱,龚明苇,田 枚
(重庆邮电大学 通信核心芯片、协议及系统应用创新团队,重庆 400065)

基于信噪比排序的MIMO-OFDM信号检测方法
郑建宏,李玉菱,龚明苇,田 枚
(重庆邮电大学 通信核心芯片、协议及系统应用创新团队,重庆 400065)
在多输入多输出(multiple-input multiple-output,MIMO)系统信号检测中,基于虚实分解的宽度优先检测算法(QR decomposition associated with the M-algorithm to MLD,QRD-M)通过QR分解和对每层星座点的筛选,实现了较低复杂度的检测,具有很好的应用前景。但该算法随收发天线数和调制阶数的增加而难以实现性能与复杂度的折衷。针对此缺点,提出了一种基于信噪比排序的信号检测改进方法。该方法在传统QRD-M算法的基础上,通过对不同接收天线进行信噪比(signal-noise ratio,SNR)排序,从信噪比最大的天线开始检测,避免了误差传播现象,从而加速树搜索过程,再结合动态门限树搜索,不断缩小搜索半径,直至找到最小累计度量值所在分支。仿真结果表明,与传统QRD-MLD算法相比,基于性噪比排序的动态门限信号检测算法能以较低的复杂度获得接近于最大似然检测的性能。
MIMO-OFDM系统;QRD-MLD算法;信噪比排序;信号检测
0 引 言
多输入多输出(multiple-input multiple-output,MIMO)技术可以实现高速率、高频谱利用率、以及高可靠性数据传输。正交频分复用(orthogonal frequency division multiplexing,OFDM)技术可以有效利用频谱资源和抗频率选择性衰落。将二者相结合形成了MIMO-OFDM,该技术在长期演进(long term evolution,LTE)和IEEE 802.11(institute of electrical and electronics engineers)中都得到了广泛的运用。在长期演进技术升级版(long term evolution-advanced,LTE-A)中,一方面利用MIMO在不增加频谱资源和天线发射功率的前提下成倍地提高了系统容量;另一方面,利用OFDM可以减少频率选择性衰落和子信道间的相互干扰,从而实现高可靠性传输[1]。在802.11ac 中,利用MIMO-OFDM将时间分集、空间分集以及频率分集有机结合起来,可支持多达8路空间流传输,极大地提高了数据吞吐量,提升了网络性能[2]。
由于MIMO-OFDM系统采用多天线收发,信道状态更为复杂,如何准确并实时地检测出MIMO系统中的多路信号已成为近年来的研究热点。各种基于MIMO-OFDM系统的信号检测算法被相继提出,其中,最大似然(maximum-likelihood,ML)算法是最优的检测算法,它对所有可能发送的信息进行遍历搜索,从而得到概率最大的信息。但ML检测计算复杂度会随着发射天线数和调制星座点个数成指数倍增长,难以用于工程实现,因此,衍生出了基于虚实分解的宽度优先检测算法(QR decomposition associated with the M-algorithm to MLD,QRD-MLD)和球形译码(QR decomposition associated with the sphere decoder,QR-SD)等次优算法[3]。
QRD-MLD和QR-SD树搜索检测算法均以远低于ML检测的复杂度获得了ML或近似ML的性能。两者不同之处在于树搜索处理的方法不同,QR-SD算法采用的是深度优先的串行检测结构,导致时延大,不利于工程中的并行实现[4]。QRD-MLD算法是在ML检测算法的基础上,通过QR分解和对每层星座点个数M的筛选,实现其性能和复杂度的折中。该算法采用并行的方式树搜索,与深度优先的QR-SD算法相比,QRD-MLD具有复杂度固定、时延小和易于并行实现的优势,这使得该算法比较适合于硬件实现[5]。因此,实际工程中主要采用宽度优先的QRD-MLD信号检测算法。
传统QRD-MLD算法中M的取值非常关键,M值取小,可能导致剔除掉最优解;M值取大,就会导致计算复杂度增加。文献[6]提出一种等效级联模型,将搜索过程分为ML搜索和QRD-M搜索2部分,虽然该方法中含有最优检测ML模块,但为了控制复杂度,此模块检测的层数不宜过多,然而,在QRD-M模块中又无法保证被抛弃的分支是否存在最终解,因此,其性能并不能得到大幅度提升。文献[7]中提出一种动态门限的方式,即每层保留的节点是通过本层最小欧氏距离加上一层的最小欧氏距离所决定,但通过仿真验证,该方法星座点筛选幅度较小,一旦发射天线数过多,其复杂度将陡然升高,文献[8]也采用动态门限的方法,由于树搜索过程中不同层的星座点累计度量值会因噪声而有所偏差,且噪声值正比于当前层数。因此,发送节点与接收节点之间的距离越小,其实际解与其他解之间的累计度量值差距就会越大。文献[8]将每层的门限值反比于当前层最优解与次优解之间的距离差,从而进行星座点的筛选。本文同样借鉴了动态门限树搜索的思想,提出一种能同时兼顾天线数和计算复杂度,且性能逼近于ML的检测方法。该方法首先对不同天线的接收信号按信噪比大小进行排序,接下来对排序后的接收信号进行动态门限树搜索,不断更新搜索半径,直至找到累计度量值最小的分支。
1 传统QRD-MLD算法
1.1 系统模型
图1为一个有Nt根发射天线以及Nr根接收天线的MIMO无线通信系统模型。

图1 MIMO系统模型框图Fig.1 Model of a MIMO system
假设发射端有Nt根发射天线,接收端有Nr根接收天线,x表示Nt×1维发送信息矩阵;y表示Nr×1维接收信息矩阵;H表示Nt×Nr维信道状态信息矩阵;n表示Nr×1维信道噪声矢量,那么MIMO系统数学模型可以表示为
y=Hx+n
(1)
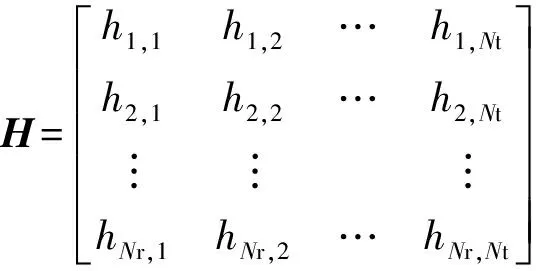
在MIMO发射端对比特数据进行信道编码,对形成的码字进行调制,接着将调制信号组合一起进行层映射、预编码,最后映射到天线端口上发送;在接收端需要利用接收信号y与信道估计得来的信道矩阵H以及噪声方差σ2来估计出发送符号矢量x,并对其进行解调处理。
1.2 传统QRD-MLD检测算法
传统的QRD-MLD算法被广泛应用到MIMO系统信号检测中,它结合QR分解以及树搜索理念,通过并行的方式对接收信号进行逐层检测,每一层通过选取M个累计度量值最小的检测结果来限制ML搜索空间。
1)首先进行QR分解,一个Nt×Nr的信道矩阵H可以分解为一个Nt×Nr的正交酉矩阵Q和一个Nt×Nr的上三角矩阵R。
H=QR
(2)
接收信号可以表示为
y=QRx+n
(3)
等式两边左乘QH,有
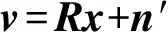
(4)
(4)式中:v=QHy,n′=QHn分别为变换后的接收信号矢量和噪声向量。将(4)式进一步展开,观察如下
(5)
2)通过QR分解将空间搜索转换为树搜索,从三角矩阵最后一层逐层计算出各层的发送信息估计,计算方法为
(6)

接着计算每个幸存节点的累计度量值,以第k层,第m个节点为例,其累计度量值可表示为
(7)
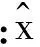
3)QRD-MLD算法从最后一层开始检测,依次计算当前层累计度量值,并从中选出Mk个累计度量值最小的节点作为下一层节点的父节点。通过对每层幸存星座点的限制加速搜索过程,最终找出层0中累计度量值最小节点所在分支,即为ML解[10]。
基于QR分解的检测算法,其搜索路径均可由树形结构表示,以4发4收MIMO系统QPSK调制为例,传统QRD-MLD(M=4)检测算法的树形结构如图2所示。
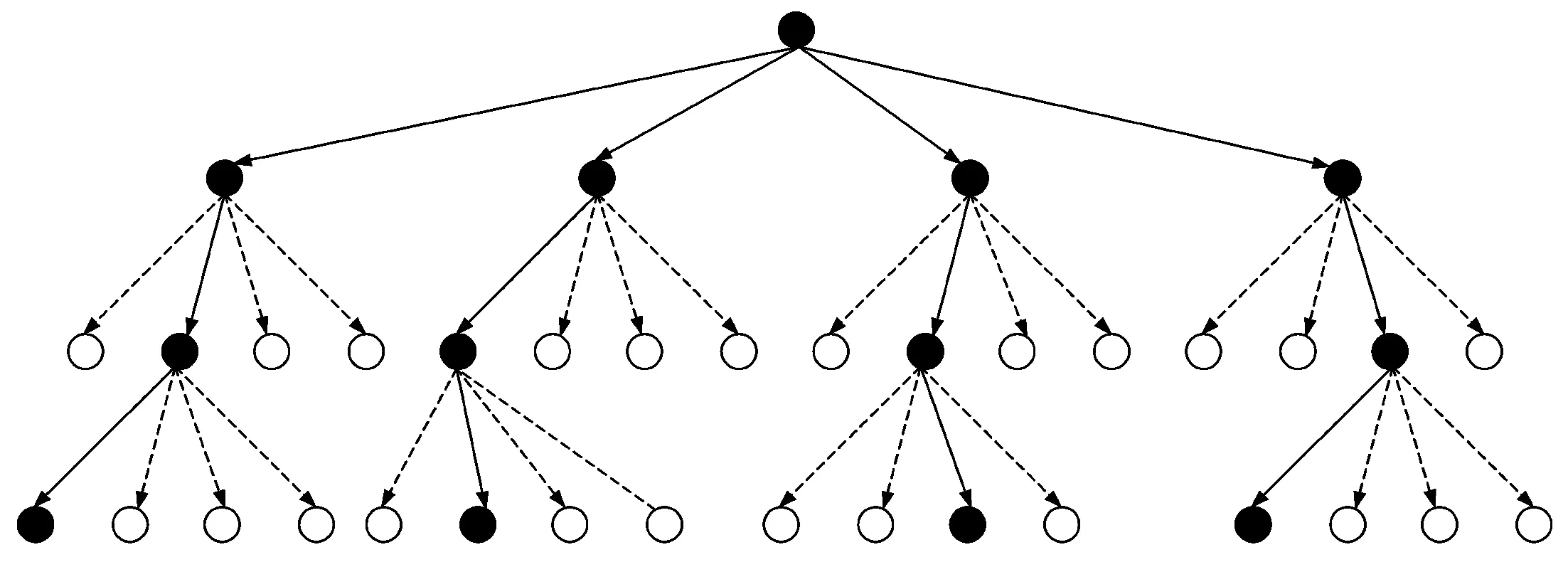
图2 QRD-MLD(M=4)树形结构Fig.2 Tree structure of QRD-MLD (M=4)
传统的QRD-MLD算法通过线性化降低了多天线对最大似然检测造成的影响,极大地降低了检测复杂度,但要使其性能逼近ML检测,M值必须尽可能的增大。然而随着层数的增加,以及调制阶数的升高,整个计算复杂度将会成指数倍增长。若为了降低检测复杂度而减小M值,在未达到底层前,累计度量值较大的分支被抛弃,但被抛弃的分支中可能存在ML最终解,从而导致系统性能降低。本文提出一种在较低复杂度情况下,通过信噪比(signal-noise ratio,SNR)排序结合动态门限树搜索的方法从而获得接近ML性能的算法。
2 针对QRD-MLD检测算法的改进
2.1 接收天线SNR排序
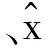
传统的QRD-MLD检测算法都是从底层开始检测,前一层的检测结果会对后一层造成影响。如果首层的信噪比过低,在层层检测的过程中累计度量值较大的分支被保留下来的机率将急剧加大,从而导致错检率升高,系统性能下降。由于QR分解后的线性检测关系可能导致误差扩散问题,因此,在MIMO系统中首层检测的准确度至关重要,信号检测顺序将直接影响整个系统性能。
在改进的方法中,为了减少错过ML解的可能性,在进行QR分解之前,首先对接收信号y=[y1,y2,…,yNr]T按照接收天线上不同信噪比大小进行排序y=[y|SNRmin,…,y|SNRmax]T,这样信噪比较大的层就能够被接收端优先检测,避免了误差传播现象,同时还减少了检测次数,降低了复杂度。应当注意的是当接收信号y的顺序变换后,其对应的H矩阵行排布也要随之变换。
2.2 动态门限树搜索
对接收天线按信噪比排序之后,接下来就对信号进行树搜索,图3为整个动态门限树搜索的全过程。
首先,通过传统QRD-MLD方法计算出第n层Mn个节点的子节点集合预判值为
(8)
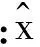
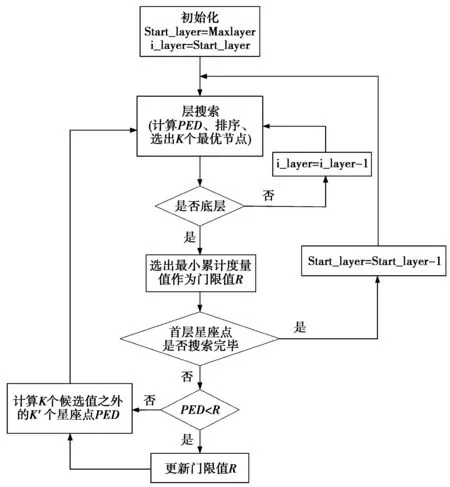
图3 动态门限搜索过程Fig.3 Search process of dynamic threshold
2.3 对数似然比计算
为了译码的准确性,译码端需要输入每个比特的软信息,即对数似然比。LLR计算公式为
(9)
由于M算法可能造成(9)式中不存在xv,n∈Sv(bk=0)或者xv,n∈Sv(bk=1)的情况,从而造成LLR(bn)无解。本文采用一种软信息计算方法,首先通过上述检测得到ML解及其度量值,然后根据得到的ML解得出其比特位的补码。接下来,通过一次树形检测计算其补码的最小度量值。最后,两值相减则得到该比特的LLR为
(10)
3 复杂度和仿真分析
QRD-MLD检测算法的复杂度是由检测过程中需要计算的总分支数所决定。以4×4天线配置为例,采用16QAM调制方式,统计算法复杂度时加、减、乘各算一次,不同层单个节点对应的复杂度分别为[3|Nr=4,6|Nr=3,8|Nr=2,10|Nr=1] 。由于改进的动态树搜索算法中每一次检测的节点数不是固定的,所以,只能用范围表示。

表1 不同方案复杂度统计Tab.1 Complexity of different method
从表1可见,改进方案的复杂度虽然比传统QRD-MLD稍有提升,但相比于ML检测,检测复杂度下降了71%~88.4%。下面通过仿真实验对改进的QRD-MLD算法性能进行验证。
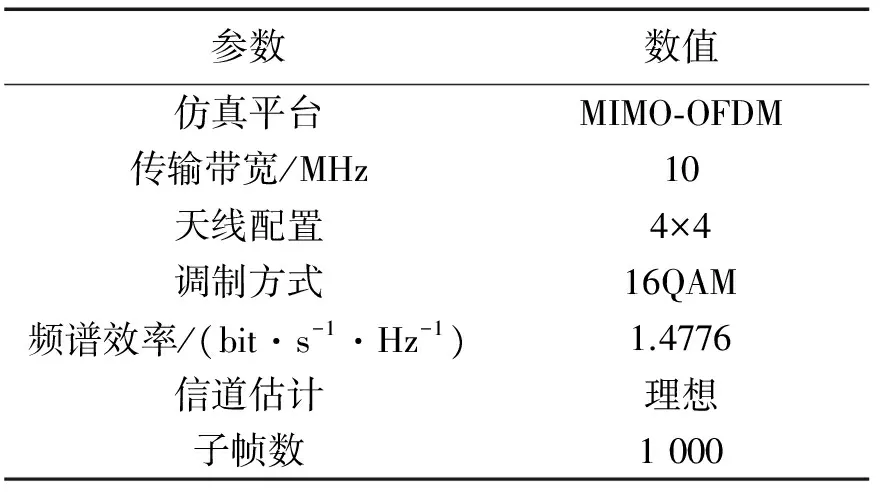
表2 仿真参数Tab.2 Simulation parameters
仿真分析采用的对比算法如下。
1)ML算法。搜索过程遍历所有的星座点,性能最优,但其复杂度随调制阶数和天线数成指数倍升高;
2)最小均方误差(minimum mean square error,MMSE)算法。选择一个合适的权值矩阵,使得其估计误差的平方的均值最小;
3)传统QRD-M。按照累计度量值大小,每层固定选出M个星座点作为下一层的父节点;
4)改进的QRD-MLD。首先通过SNR排序加快了搜索速度,再加上动态门限树搜索极大地降低了错失ML解的可能性。
图4,图5分别给出了EPA5和EVA70 2种不同信道模型下,不同算法的误比特率(bit error ratio,BER)与SNR关系曲线。
从图4,图5中可以看出,在相同信噪比条件下,基于信噪比排序的QRD-MLD算法相比于传统算法有明显的性能提升。这是由于传统的QRD-M算法每层只保留固定的M个星座点,然而在抛弃的星座点中可能存在ML最终解。因此,在改进算法中采用动态门限树搜索的方法,在一次传统的树搜索结束后,再回到底层将之前丢弃的节点与最终的累计度量值相比较,若找到小于累计度量值的节点,则更新门限继续搜索,直至找到ML解,这使得其性能几乎等同于ML算法;同时,又由于在QR分解前对不同天线进行了SNR排序,优先检测了信噪比较大的层,在降低错失最优解机率的同时又加快了搜索速度。与传统QRD-MLD算法相比,基于信噪比排序的检测算法以牺牲较小的复杂度获得了更好的系统性能。
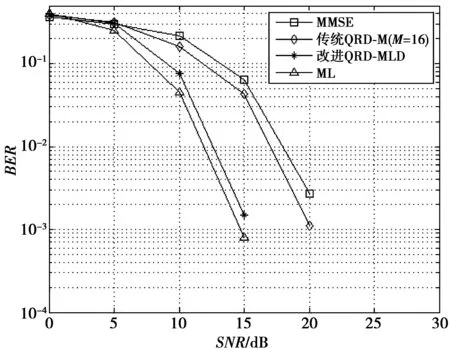
图4 EPA5信道模型下BER性能Fig.4 BER curves of EPA5

图5 EVA70信道模型下BER性能Fig.5 BER curves of EVA70
4 结束语
本文从QR分解、树搜索、求解LLR这3个方面入手对传统QRD-MLD检测算法进行了改进。通过对不同天线SNR排序结合动态门限树搜索的方法,在有效地控制复杂度的同时提升了系统性能。最后,通过算法仿真验证了该方法在不同信道条件下的性能曲线。该改进算法能够实现系统性能和复杂度的折衷,可以在相对较低的复杂度条件下获得更接近于最大似然检测的性能。从实际应用和系统考虑,这种改进是必要可行的。
[1] NEE R PRASAD R. OFDM for wireless multimedia communications[M]. London: Artech House, 2000: 55-78.
[2] 马满仓,郑建勇,郭静,等.WLAN标准IEEE802.11ac/ad及其关键技术[J].电信技术,2012(4):75-77. MA Mancang, ZHENG Jianyong, GUO Jing, et al. WLAN standard IEEE802.11ac/ad and key technologies[J]. Telecommunications Technology, 2012(4):75-77.
[3] CHIN W H. QRD based tree search data detection for MIMO communication systems[J]. Proceedings of the IEEE Vehicular Technology Conference, 2005, 3(3):1624-1627.
[4] JALDEN J, OTTERSTEN B. On the complexity of sphere decoding in digital communications[J]. IEEE Transactions on Signal Processing, 2005, 53(4):1474-1484.
[5] MILLINER D L, BARRY J R. A layer-adaptive M algorithm for multiple-input multiple-output channel detection[C]//IEEE 8thWorkshop on Signal Processing Avances in Wireless Communications. Helsinki: IEEE Press, 2007: 1-5.
[6] LIU L, WANG J, YAN D, et al. An Improved QRD-M Detection Algorithm for MIMO Communication System[C]//IEEE 2009 IITA International Conference on Control, Automation and Systems Engineering. Zhangjialie, China: IEEE Press, 2009: 496-499.
[7] LIM H, JANG Y, LI T, et al. Improved QRD-M algorithm based on adaptive threshold for MIMO systems[C]//IEEE 2014 Sixth International Conference on Communication Systems and Networks, Bangalore: IEEE Press, 2014: 1-4.
[8] FAN W, LIU Y, WANG Z, et al. A new dynamic K-best SD algorithm for MIMO detection[C]//IEEE 2014 Sixth International Conference on Wireless Communications and Signal Processing. Hefei: IEEE Press, 2014: 1-5.
[9] 龚丽莎, 尹露, 龚赛丹,等. 基于空间调制的天线选择和能效优化算法[J]. 电子科技大学学报, 2014(4):497-501. GONG Lisha, YIN Lu, GONG Saidan, et al. Transmit Antenna Selection and Energy Efficiency Improvement for Spatial Modulation[J]. Journal of University of Electronic Science and Technology of China, 2014(4):497-501.
[10] WEI H, FUJINO T, KOJIMA T. Adaptive candidate selection scheme in QRM-MLD algorithm for MIMO detection[C]//IEEE International Conference on Wireless & Mobile Computing, Networking and Communications(Wimob).Barcelona,Spain:IEEE,2012,14(1):502-506.
(编辑:刘 勇)
The National No. 3 Major Program (2015ZX03001010-003)
In the MIMO(multiple-input multiple-output) communication system, QRD-M (QR decomposition associated with the M-algorithm to MLD) algorithm has a good application prospect because it employs QR decomposition and constellation points screening of each layer to accomplish low complexity signal detection. However, when the number of the transmitting and receiving antennas increases, it is difficult to achieve a good tradeoff between system performance and implementation complexity. In order to solve the problem, this paper proposes a novel signal detection method by using SNR(signal-noise ratio) sorting. Based on the breadth-first parallel structure of QRD-M algorithm, the proposed method first sorts the values of SNR of receiving antennas to avoid the error propagation and therefore speeds up the tree search process. Combining with dynamic threshold search method, the search radium is reduced until reaching the branch of the minimum accumulated squared Euclidean distances. The simulation results show that the proposed method can approach the performance of the maximum likelihood detection with lower complexity.
MIMO-OFDM systems; QRD-MLD algorithm; SNR sorting; signal detection
2016-07-06
2017-03-11 通讯作者:李玉菱 li_yuling@qq.com
国家03重大专项(2015ZX03001010-003)
10.3979/j.issn.1673-825X.2017.04.001
TN929.5
A
1673-825X(2017)04-0427-06
Signal detection method based on SNR sorting for MIMO-OFDM systems
(Communication Core Chip, Protocols and Application Innovation Team, Chongqing University of Posts and Telecommunications,Chongqing 400065, P.R. China)

郑建宏(1961-),男,重庆人,教授、博士生导师,主要研究方向为通信核心芯片、协议与系统应用技术。E-mail: zhengjh@cqupt.edu.cn。

李玉菱(1991-),女,重庆人,硕士研究生,主要研究方向为LTE-A无线通信信号检测与算法研究。E-mail: li_yuling@qq.com。 龚明苇(1991-),男,湖北宜昌人,硕士研究生,主要研究方向LTE-A无线通信信号检测算法研究。E-mail: 251076366@qq.com。 田 枚(1991-),女,湖北孝感人,硕士研究生,主要研究方向为LTE-A信道估计算法研究。E-mail: 1120258343@qq.com。
ZHENG Jianhong, LI Yuling, GONG Minwei, TIAN Mei

