“涂色问题”的变式探究

江苏 王佩其

(作者单位：江苏省太仓市明德高级中学)

“涂色问题”的变式探究

“涂色问题”是高考中比较常见的一类计数问题，具有一定的难度，能全面考查同学们的创新思维能力、分析问题与观察问题的能力.解决这类问题的关键是合理采用分类思想，并结合独特的视角，下面让我们一起来探究.

一、由四棱锥的顶点涂色引出的问题

【引例】如图所示，将一个四棱锥的每一个顶点涂上一种颜色，并使同一条棱上的两端异色，如果只有5种颜色可供使用，求不同的涂色方法总数.

【分析】涂色问题是常见的计数应用问题，可从选颜色、选顶点进行分类、分步，从不同角度解决问题.

【解析】方法一：可分为两步进行，先将四棱锥一侧面三顶点涂色，然后再分类考虑另外两顶点的涂色数，用分步乘法计数原理即可得出结论.由题设，四棱锥S-ABCD的顶点S、A、B所涂的颜色互不相同，它们共有5×4×3=60(种)涂色方法.

当S、A、B涂好时，不妨设其颜色分别为1、2、3，若C涂2，则D可涂3或4或5，有3种涂法；若C涂4，则D可涂3或5，有2种涂法；若C涂5，则D可涂3或4，有2种涂法.可见，当S、A、B已涂好时，C、D还有7种涂法，故不同的涂色方法有60×7=420(种).

方法二：以S、A、B、C、D顺序分步涂色.

第一步，S点涂色，有5种方法；

第二步，A点涂色，与S在同一条棱上，有4种方法；

第三步，B点涂色，与S、A分别在同一条棱上，有3种方法；

第四步，C点涂色，也有3种方法，但考虑到D点与S、A、C相邻，需要针对A与C是否同色进行分类，当A与C同色时，D点有3种涂色方法；当A与C不同色时，因为C与S、B也不同色，所以C点有2种涂色方法，D点也有2种涂色方法.由分步乘法、分类加法计数原理得不同的涂色方法共有5×4×3×(1×3+2×2)=420(种).

方法三：按所用颜色种数分类.

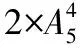
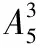
【评注】(1)解决涂色问题，一定要分清所给的颜色是否用完，并选择恰当的涂色顺序.

(2)切实选择好分类标准，分清哪些可以同色，哪些不同色.

二、将四棱锥变为被对角线分成四部分的矩形

【探究1】如图，矩形的对角线把矩形分成A，B，C，D四部分，现用5种不同的颜色给这四部分涂色，每部分涂1种颜色，要求共边的两部分颜色互异，则共有 种不同的涂色方法.

【解析】区域A有5种涂色方法；区域B有4种涂色方法；区域C的涂色方法可分两类：若C与A涂同色，区域D有4种涂色方法；若C与A涂不同色，此时区域C有3种涂色方法，区域D也有3种涂色方法.所以共有5×4×4+5×4×3×3=260(种)涂色方法.

【评注】本题若直接利用分步乘法计数原理来求，则会导致错解，其错误在于没有注意到依次涂完A、B、C三个区域后，区域D的涂色方法数要受到A、C两区域的影响，因此要对A、C颜色是否相同进行分类.另外，对于此类涂色问题也要注意所给颜色是否必须用完.

三、将四部分变为五个区域

【探究2】如图所示，一个地区分为5个行政区域，现给该地区的地图涂色，要求相邻区域不得使用同一种颜色，现有4种颜色可供选择，则涂色方法共有 种.

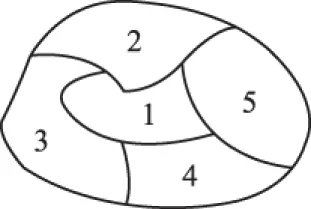
【解析】因为区域1与其他4个区域都相邻，首先考虑区域1，有4种涂法，然后再按区域2,4同色和不同色，分为两类：

第1类，区域2,4同色，有3种涂法，此时区域3,5均有2种涂法，共有4×3×2×2=48种涂法；

第2类，区域2,4不同色，先涂区域2，有3种方法，再涂区域4，有2种方法，此时区域3,5都只有1种涂法，共有4×3×2×1×1=24种涂法.

根据分类加法计数原理，共有48+24=72种满足条件的涂色方法.

【评注】本着特殊区域优先涂色的原则，故先涂与其他四个区域都相邻的区域1.而区域2,4(或区域3,5)相对于区域1所处位置相同，故涂色时对它们同时进行.可见涂色必须考虑先后次序.

四、将五个区域变成九个区域

【探究3】用红、黄、蓝三种颜色去涂图中标号为1，2，…，9的9个小正方形(如图所示)，使得任意相邻(有公共边)的小正方形所涂颜色都不相同，且标号为1，5，9的小正方形涂相同的颜色，则符合条件的所有涂法共有 种.

123456789

【解析】把区域分为三部分.第一部分1，5，9，有3种涂法.第二部分4，7，8，当5，7同色时，4，8各有2种涂法，共4种涂法，当5，7异色时，7有2种涂法，4，8均只有1种涂法，故第二部分共有4+2=6(种)涂法.第三部分与第二部分一样，共6种涂法.

由分步乘法计数原理，可得共有3×6×6=108(种)涂法.

【评注】由于对角线上的三个区域最特殊，所以先给它们涂色，继而再给第二部分4，7，8和第二部分2,3,6涂色，在同一部分涂色采用分类计数原理，不同部分涂色的计数采用分布计数原理.

从以上探究可以看出，在解决涂色问题的过程中，并不一定是单一的分类或分步，而是可能同时应用两个计数原理，即分类时，每类的方法可能要运用分步完成，而分步时，每步的方法数可能会采取分类的思想求.分类的关键在于要做到“不重不漏”，分步的关键在于要正确设计分步的程序，即合理分类，准确分步.

【变式练习1】如图，花坛内有5个花池，有5种不同颜色的花卉可供栽种，每个花池内只能种一种颜色的花卉，相邻两池的花色不同，则栽种方案的种数为

( )

A.180 B.240

C.360 D.420

【答案】D

【变式练习2】用n种不同颜色为广告牌着色(如图甲)，要求在①、②、③、④个区域中相邻(有公共边界)的区域不用同一种颜色.

(1)当n=6时，为图甲着色时共有多少种不同的着色方法.

(2)若为图乙着色时共有120种不同的着色方法，求n.

【解】完成着色这件事，共分四个步骤进行，可依次考虑①、②、③、④着色时各自的方法数，再由乘法原理确定总的着色方法数.

(1)为①着色有6种方法，为②着色有5种方法，为③着色有4种方法，为④着色也有4种方法.所以共有着色方法：6×5×4×4 = 480 (种).

(2)与(1)的区别在于与④相邻的区域由两块变成了三块，同理不同的着色方法数是：n(n-1)(n-2)(n-3).

由n(n-1)(n-2)(n-3)=120得(n2-3n)(n2-3n+2)-120=0，

(作者单位：江苏省太仓市明德高级中学)