二轮复习要重视教材
——以平面向量数量积为例
浙江 刘志昌 李承法
(作者单位:浙江省开化中学)
二轮复习要重视教材
——以平面向量数量积为例

二轮复习要重视教材,能帮助同学们跳出题海、高效复习的唯有教材.平面向量的数量积是每年高考的重点和热点内容,且常与三角函数、数列、解三角形、解析几何等交汇命题,常考常新.解答此类问题或转化为代数运算,或利用其几何意义,其转化途径主要是利用平面向量数量积的公式和性质,而这些解题思路,其实就在教材中!
一、横看成岭侧成峰,远近高低各不同——重视平面向量数量积之投影形式

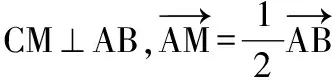

图1
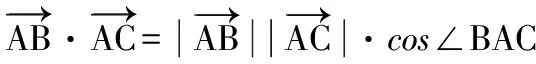
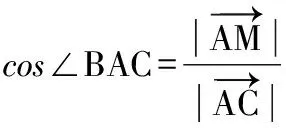
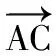
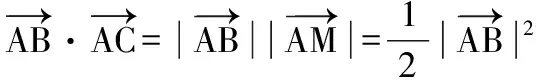


( )
A.只与圆C的半径有关
B.只与弦AB的长度有关
C.既与圆C的半径有关,又与弦AB的长度有关
D.是与圆C的半径和弦AB的长度均无关的定值
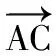
【评注】本例是教材习题的改编,而教材中的这道习题本身就是平面向量数量积的几何意义的直接应用,这是一道直接源于课本的试题.在二轮复习过程中多关注研究课本习题、思考题,进行归类,那么就能很好地帮助同学们整合知识.
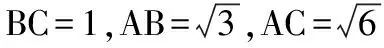

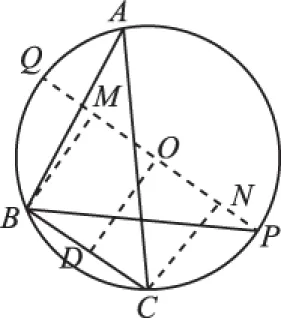
图2

图3
【评注】方法二,运用代数运算,解三角形,结合运用特殊化思想,取B,C为特殊点,然后进行数量积的坐标运算,解决问题;而方法一,则按照平面向量数量积的投影意义思路来求解就比较简捷.由此可知,当数量积中有一个向量的模长为定值(或投影与另一向量的模长关系确定)时可以用平面向量数量积的投影形式解决问题.
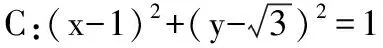
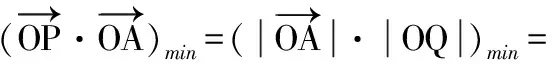
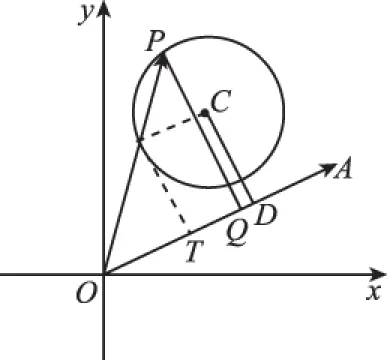
图4

( )
A.4 B.5 C.7 D.9
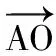

图5
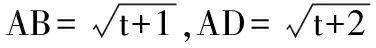
( )
A.1 B.2 C.tD.2t

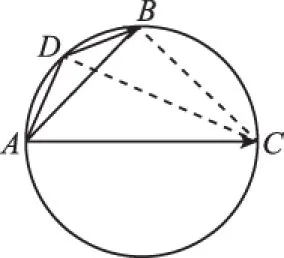
图6
二、不识庐山真面目,只缘身在此山中——善用平面向量数量积之余弦定理形式
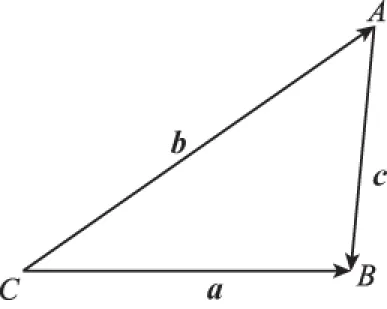
图7


图8
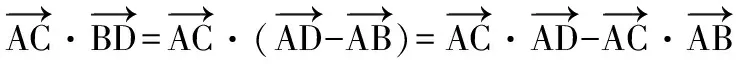
在△ABC中,由平面向量数量积余弦定理形式知:
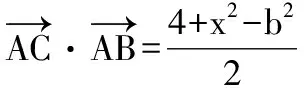
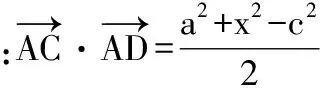
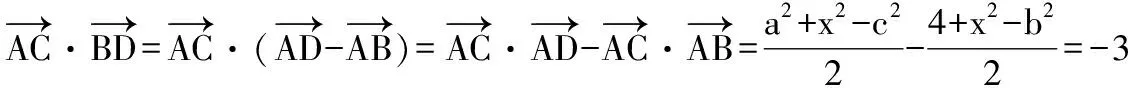
即c2=a2+b2+2.
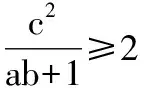
【评注】利用平面向量数量积之余弦定理形式较快地解决了这个问题.正如教科书108习题B组第5题所说,利用好向量数量积可以容易地推导关于三角形、四边形、圆等平面图形的一些性质.从此例可以发现常用的一些技巧方法,结论,其实很多的都来源于课本,只要我们能真正地理解课本,挖掘课本中的隐含知识、延伸知识,很多的问题的解决方法都可以在课本上找到.因此高三二轮复习时,不但不要完全的脱离课本,而且要多与课本相联系,多多关注到课本例习题.
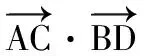
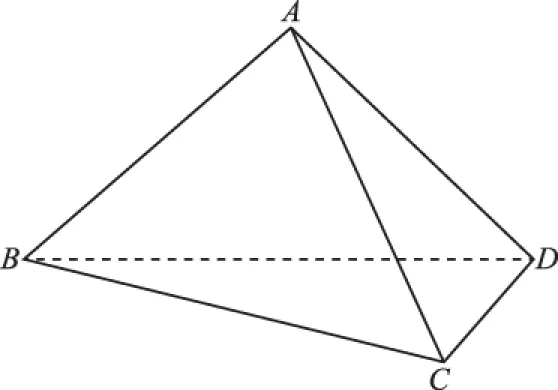
图9

三、轻沙走马路无尘——巧用平面向量数量积之极化恒等式形式
人教版必修四教材第109页平面向量应用举例中有此例:如图10,你能发现平行四边形的对角线长度和两条邻边长度之间的关系吗?
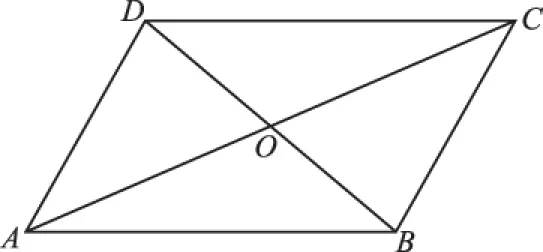
图10
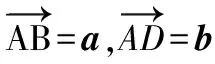
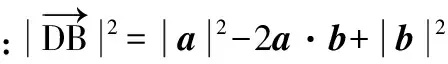
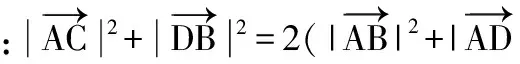
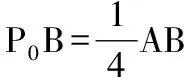
( )
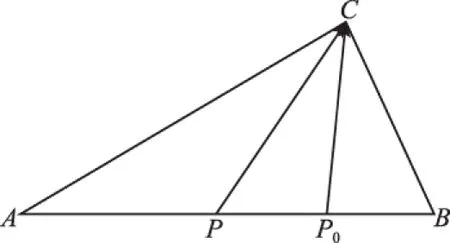
图11
A.∠ABC=90°
B.∠BAC=90°
C.AB=AC
D.AC=BC


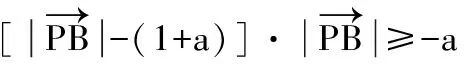
∴Δ=(1+a)2-4a≤0,得a=1,
∴H为AB的中点,∴AC=BC,故选D.

图12
方法二:(利用平面向量数量积之极化恒等式)
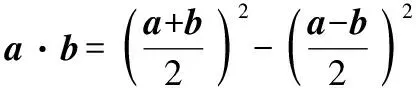
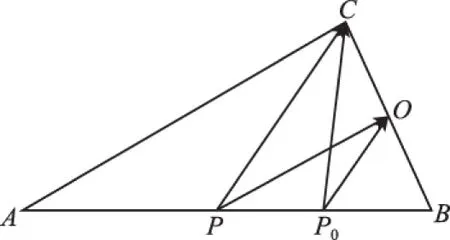
图13




∴OP0⊥BC,即有:当AP⊥BC时,P为BC的中点.
∴AC=BC,故选D.
【评注】此题方法一、二分别利用了平面向量数量积的几何意义(投影形式)和极化恒等式,转化为可借助图中平面几何知识就可以解决问题,解法显得快捷简洁.
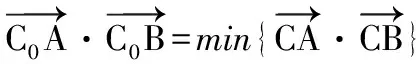
( )
A.C0M⊥AB
B.C0M⊥l,其中l是抛物线过C0的切线
C.C0A⊥C0B

答案:B
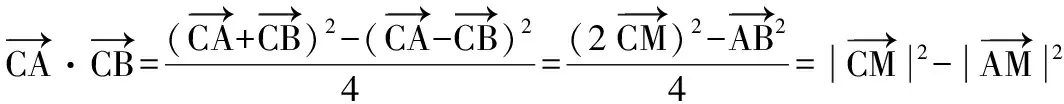
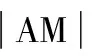

∴C0M⊥l,其中l是抛物线过C0的切线.
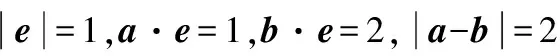
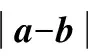
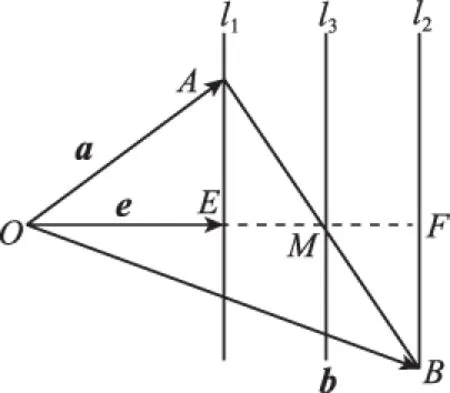
图14

(作者单位:浙江省开化中学)

