求曲线轨迹方程的策略

河北 宋连筠

(作者单位：河北省衡水市郑口中学)

求曲线轨迹方程的策略

求曲线的轨迹方程是高考的常考题型，往往在解答题的第一问中出现，有时也在选择、填空题中出现.常考查轨迹方程的求法，以及利用曲线的轨迹方程研究曲线的几何性质.解题的关键是如何找到动点坐标所满足的等量关系.求轨迹方程的常用方法一般有如下四种，以下分别进行讨论.

一、直接法求轨迹方程

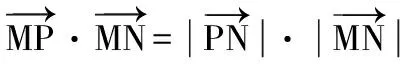
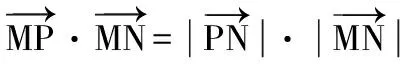
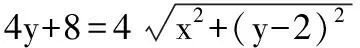
整理，得x2=8y.

即动点P的轨迹C为抛物线，其方程为x2=8y.

【评注】直接法是求轨迹方程的基本方法，所谓直接法求轨迹方程，即题目中的条件有明显的等量关系，或者可以利用平面几何知识得到等量关系，当所求动点要满足的条件简单明确时，直接按“建系，设点，列出条件，代入坐标，整理化简，限制说明”五个基本步骤，列出含动点M(x，y)的关系式，进而求得轨迹方程.

【解析】设出动点坐标，利用向量数量积公式及模长公式，即可求动点P的轨迹C.

设动点P(x，y)，又点M(4,0)、N(1,0)，

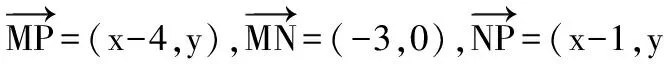
所以(x2-8x+16)=4(x2-2x+1)+4y2，

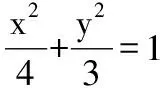
所以轨迹C是焦点为(±1,0)，长轴长2a=4的椭圆.

二、定义法求轨迹方程

【例2】已知圆心为F1的圆的方程为(x+2)2+y2=32，F2(2,0)，C是圆F1上的动点，F2C的垂直平分线交F1C于M，求动点M的轨迹方程.

【解析】因为F2C的垂直平分线交F1C于M，所以 |MF2|=|MC|.

【评注】圆锥曲线的定义揭示了动点的本质特征.利用定义法求轨迹问题时，往往应先考虑动点满足的距离关系，判断它是否满足熟悉的几种曲线的定义，如圆、椭圆、双曲线、抛物线的定义，进而求出该曲线的方程.定义法求轨迹的关键是紧扣解析几何中有关曲线的定义，灵活应用定义，而圆锥曲线的方程随坐标系的不同而不同，因而掌握定义是根本.

三、代入法求轨迹方程

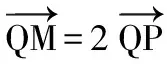
【解析】设点P的坐标为(x0，y0)，点M的坐标为(x，y)，则点Q的坐标为(0，y0).

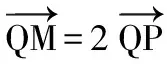
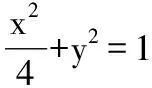
【评注】如果轨迹动点M(x，y)依赖于另一动点P(x0，y0)(也称相关点)，而P(x0，y0)又在某已知曲线上，则可先列出关于x、y、x0，y0的方程组，利用x、y表示出x0，y0，把x0，y0代入已知曲线方程便得动点P的轨迹方程.这就是代入法求轨迹的方程.当题目中有多个动点的时候，将其他动点的坐标用所求动点P的坐标(x，y)来表示，再代入到其他动点要满足的条件或轨迹方程中，整理即得到动点P的轨迹方程.

【变式3】过抛物线y2=4x的焦点F作直线与抛物线交于P、Q两点，当此直线绕焦点F旋转时，弦PQ中点的轨迹方程为 .

得(y1-y2)(y1+y2)=4(x1-x2)，

设PQ中点为M(x,y)，当x1≠x2时，

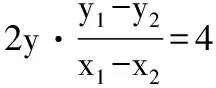
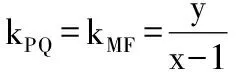
即y2=2(x-1).

当x1=x2时，易得弦PQ的中点为F(1,0)，也满足所求方程.

故所求轨迹方程为y2=2(x-1).

四、参数法求轨迹方程

【解析】 直线l过点M(0，1)设其斜率为k，则l的方程为y=kx+1.

将①代入②并化简，得(4+k2)x2+2kx-3=0，

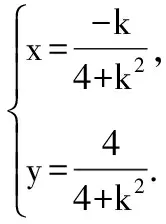
当k不存在时，A、B中点为坐标原点(0，0)，也满足方程③，所以点P的轨迹方程为4x2+y2-y=0.

【评注】如果轨迹动点M(x，y)的坐标之间的关系不易找到，也没有相关点可用时，可先考虑将x、y用一个或几个参数来表示，消去参数即可得轨迹方程.参数法中常选角、斜率等为参数，分别求出动点坐标x，y与参数的关系式，得出所求轨迹的参数方程，消去参数即可，此即为参数法.

【变式4】动圆C:(x-1)2+y2=1，过原点O作圆的任一弦，求弦的中点的轨迹方程.

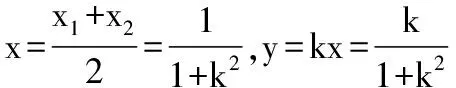
(作者单位：河北省衡水市郑口中学)