高一数学分层作业实施过程中存在的问题及对策
连兰 梁芝怀
【摘 要】本文尝试从“以人为本”的视角,选取高一两个班共67名学生为研究对象,开展分层作业的准实验研究,分析分层作业实施过程中存在的问题,提出解决对策,力争提升数学课堂效果,并让每个学生在适合自己的作业中取得成功,获得轻松、愉快、满足的心理体验。
【关键词】高一数学 分层作业 存在问题 对策
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)06B-0015-04
作业是反馈教学效果的重要手段之一,它既能使学生巩固已学知识,又能发展学生能力,培养学生的创新精神与意识。但是人存在先天性的差异,如果教师不论客观对象如何,不论人的能力差别有多大,都一味地按统一标准来要求,忽视了学生的个性特点,那么势必会打击一部分学生的积极性,造成许多负面影响,无形中使一部分学生厌恶学习,增加一种心理压力。为此,我们课题组在学校科研处罗祥沛主任的带领下开展分层作业的准实验研究,在教学中尝试实施分层作业,对不同的学生进行分层布置,对作业量、作业难度和作业方式作了适当的调整,力争使每个学生在适合自己的作业中都能取得成功,获得轻松、愉快、满足的心理体验。
一、实施的过程
(一)实施思路
本课题组的研究选取了两个高一班作为本次实验研究对象,即高一(1)班和高一(2)班,共 67 名学生。其中高一(2)班作为实验组,有 33 人,开展渗透分层作业的教学;高一(1)班作为对照组,有 34 人,开展自然状态下的常规教学。对高一年级分层作业的实践研究,实施了半个学期。
在本研究中,采用的是实验研究中的实验组与对照组前测与后测设计。将高一上学期期中考试数学成绩作为研究的基础,跟踪学生的高一上学期后半学期考试的数学成绩,分析实验班和对照班中学生数学成绩的变化,以评价分层作业的实施效果。
(二)实验组分层作业的具体实施过程
按照高一上学期的期中考试成绩,从高到低,分为两个层次,刚好划分的分数线为 130 分。不低于 130 分的有 16 名学生,作为第一层;低于 130 分的有 17 名学生,作为第二层。在学习了一个新知识点后,每层的组长于当天发下分层作业给各层的同学去做,于第二天收齐并交给老师批改,然后将参考答案贴在教室后墙上以供同学们参考。老师批改结束后登分,并选取一些典型性的问题于课堂上讲评。
二、研究数据分析与结论
(一)实验组与对照组的实验前测比较
实验组中,在期中考试的平均分是 129.3636,标准差为12.3142;对照班期中考试的平均分是 123.9118,标准差为12.6787。为了更直观地反映两个班的成绩,我们画出两个班考试成绩分布直方图(如图1所示)和雷达图(如图 2 所示)。
(注:实方<系列1>表示实验组成绩,虚方<系列2>表示对照组成绩)
图1 两个班考试成绩分布直方图
图2 两个班考试成绩分布雷达图
从分布图上看,实验组的数据绝大部分均匀地分布在对照组之上,实验成员之间除了数值外具有很好的一致性,个体之间的差异程度很小,为本次实验研究提供很好的样本,我们也可以从雷达分布图上看出这种结果。
(二)实验班的分层作业在实施过程中的比较
通过对期中考试、其中的四次作业、两次测验和期末考试情况进行详细分析,得到第一层和第二层学生成绩情况的图表。为了更好地比较两组差异较大的数据,我们引入差异系数进行刻画。将一组数据的标准差与算术平均数的百分比称为差异系数,计算公式为,其中 GV 表示差异系数,是标准差,是平均数。差异系数是刻画数据离散程度的量,差异系数越大数据越离散,差异系数越小则数据越集中。
图3 第一层学生的期中考试、四次作业、两次测验和期末考试
成绩图表
图4 第二层学生的期中考试、四次作业、两次测验和期末考试
成绩图表
(注:期中考试总分 150 分,每次作业总分 30 分,第一次测验总分 150 分,第二次测验总分 100 分,期末考试总分 150分)
在实验组内,第一层和第二层学生的四次作业成绩的标准差都呈现增大趋势,并且从原始数据统计来看,第一层学生的成绩的差异系数分别为 8.8133%,8.1675%,33.7028%,22.5150%;第二層学生的成绩的差异系数分别为 6.8026%,24.7284%,27.3861%,30.6257%。可见,随着分层作业的实施,两层学生成绩的差异系数均变大。由图 3 图 4 可见,数据的标准差也在增大,由差异系数可知,第二层学生作业成绩的分布比第一层更为离散。
通过对第一层学生共 16 人的期中考试和期末考试成绩进行配对样本的 t 检验(分析接受了分层作业处理后成绩是否产生变化),得到以下的结果(如表 1 所示)。
表1 第一层学生的期中、期末考试成绩的 t 检验表
成对样本统计量
均值 N 标准差 均值的标准误
对 1 期中考试(150分) 139.00 16 3.830 .957
期末成绩(150分) 125.75 16 10.580 2.645
成对样本相关系数
N 相关系数 Sig.
对 1 期中考试(150分) & 期末成绩(150分) 16 .625 .010
成对样本检验
成对差分 t df Sig.(双侧)
均值 标准差 均值的标准误 差分的 95% 置信区间
下限 上限
对 1 期中考试 - 期末成绩 13.250 8.714 2.178 8.607 17.893 6.082 15 .000
从该层 16 人的数据分析中得知,成对检验的 t 值是 6.082,显著性水平 sig.=0.000<0.05。
由检验的结果可知,期中考试与期末考试的成绩有显著差异,并且期中考试与期末考试成绩的相关系数是 0.625,具有较强的相关关系。由此可见,若忽略其他因素的影响,分层作业对第一层学生最终学习的成绩贡献率大约为 37.5%。
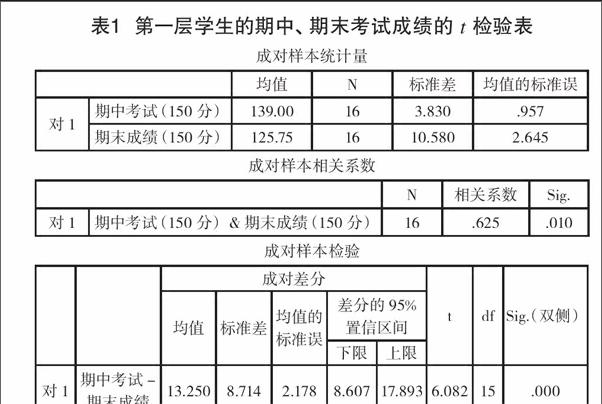
通过对第二层学生共 17 人的期中考试和期末考试成绩进行配对样本的 t 检验(因为同一群体接受了分层作业前和分层作业后两种不同的处理),得到以下的结果(如表 2所示)。
表2 第二层学生的期中、期末考试成绩的 t 检验表
成对样本统计量
均值 N 标准差 均值的标准误
对 1 期中考试 120.29 17 10.844 2.630
期末考试 113.06 17 13.363 3.241
成对样本相关系数
N 相关系数 Sig.
对 1 期中考试 & 期末考试 17 .519 .033
成对样本检验
成对差分 t df Sig.(双侧)
均值 标准差 均值的标准误 差分的 95% 置信区间
下限 上限
对 1 期中考试 - 期末考试 7.235 12.075 2.929 1.027 13.444 2.470 16 .025
成对样本检验的 t 值等于 2.470,显著性水平 sig.=0.25<0.05,说明分层作业后的测试成绩比与分层前的成绩有显著差异,而且期中考试和期末考试的成绩相关系数是 0.519,并不具有很强的相关关系。换言之,若忽略其他因素的影响,在实施分层作业后,可以认为分层作业对期末考试成绩贡献率为 48.1%。其实,我们更加关心造成这种差异的具体成因。
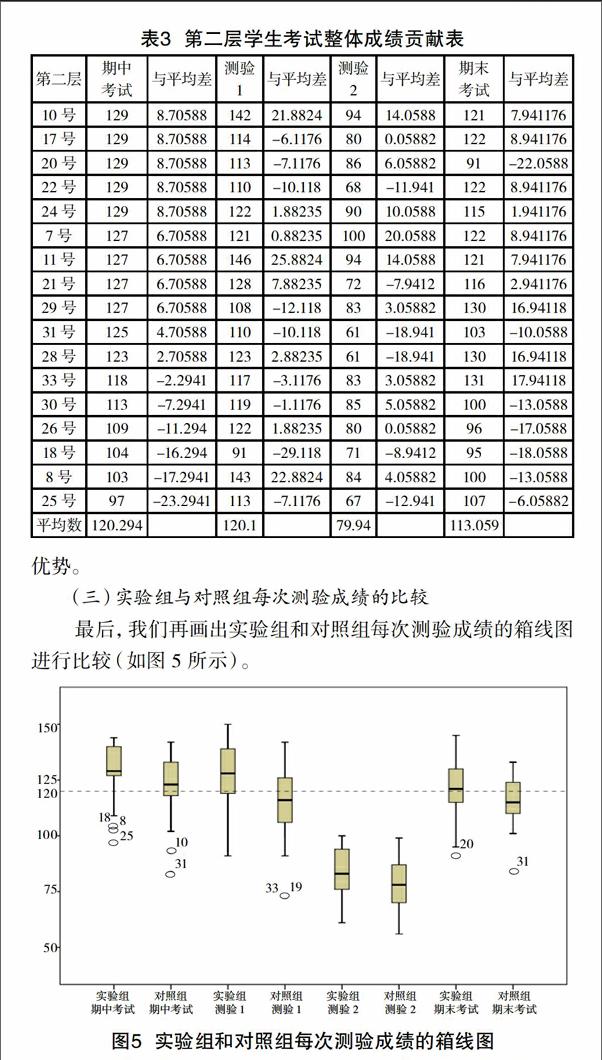
通过对第二层学生的原始成绩分析,列出下表(如下页表 3 所示)。
在原始数据中,通过对本层学生成绩的简单统计,发现分层作业后,成绩排在前四分之一和后四分之一的学生波动特别大,在期中考试和期末考试的对比中没有发挥出应有水平,两者对均值的总体贡献值都不高;相比之下处于中间段的学生,通过期中成绩和期末成绩的对比,在成绩的平均贡献率上凸显优势。
(三)实验组与对照组每次测验成绩的比较
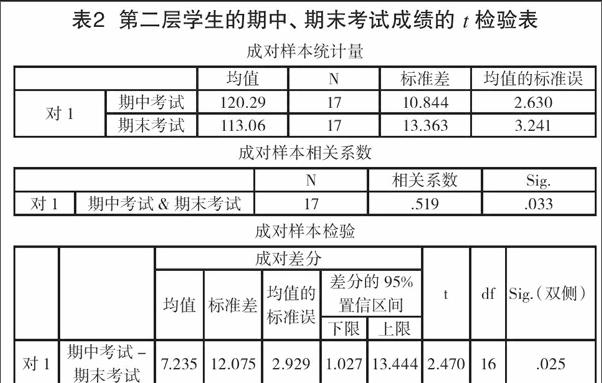
最后,我们再画出实验组和对照组每次测验成绩的箱线图进行比较(如图 5 所示)。
图5 实验组和对照组每次测验成绩的箱线图
从总体成绩来看,通过一系列分层作业的实施推进,除了测验 2 以外,实验组高分段(图中不低于 120 分)的学生中,箱线图中箱图总体呈上移趋势,也就是说高分段的学生呈集中分布。在对照组中,高分段的学生分布的比重在减少,进一步可见,数据集中分布在 110 分至 120 分的区间内。
(四)研究结论
从分层作业实验的分析结果看,主要得到以下的统计推断:
(1)分层作业对成绩优异(第一层学生)的学生最终成绩有一定贡献率,更重要的是分层作业后使得成绩的分布更加集中。
(2)对于成绩处于第二层的学生,对中间部分的学生的作用最为显著,有明显的提高作用。对该层的整体来说大约达到的成绩贡献率为 48.1%。
(3)分层作业后高分段的学生呈集中分布,在不分层的班级中高分段的学生分布的比重在减少。
三、分层作业在实施过程中存在的问题
(一)分层的依据没有标准
本次研究主要根据实验班学生的一次期中考试成绩来进行分层,分两层,对这两层的学生采用不同难度、不同内容的实施策略。实际上,一次考试并不能反映学生的真实思维水平。
(二)分层作业的设置梯度不够明显
本次研究把实验班分为两层来布置作业,从学生完成作业的成绩来看,对学生“最近发展区”的题目设置不够多。如第一次作业中,设置作业满分为 30 分,而第一层学生获得 27 分至 30 分的就有 13 人,占本层的 81.25%;第二层学生获得 27 分至 30 分的就有 16 人,占本层的 94.12%。
(三)分层的评价略显单一
本次研究主要是跟踪学生的高一上学期后半学期考试的数学成绩,分析实验班和对照班中学生数学成绩的变化,以评价分层作业的实施效果,评价略显单一。
(四)分层作业的实验样本的范围较小
本次准实验研究的对象是成绩优异的学生,对其他水平的学生没有开展实验,实验范围较小,实验结果的普遍性意义还不大,未能充分说明分层作业对所有高一学生是否均有效。
四、提出的对策
(一)做好学生的动员
做好学生的思想工作是我们实验能否顺利进行的关键。由于实验班与对照班均是由同一位数学教师授课,而作业布置的不同势必引起学生的不理解,因此,实验前老师向学生详细介绍本课题研究开展的必要性,消除学生的顾虑,同时要求学生积极配合老师,克服困难,完成老师布置的相关任务。
(二)合理地划分学生层次
学生分层就是根据学生的个性特征、认知结构、接受能力将全班学生分开几个层次,并根据不同层次的学生布置合适的作业。根据问卷调查得分和高一上学期考试成绩这两个项目总和来划分层次,按分数从高到低来排序,每个班分为两层。
(三)分层作业的设置梯度明显
每一层次的学生所拿到的作业都是具有明显的梯度性的,作业可相应分为基础练習题、灵活应用题、综合提高题三个层次。
(1)基础练习题:基本概念、公式、法则、性质、规律等知识,数学基本技能的训练的练习。这一层次的习题量稍多,但内容简单,属应知应会的范畴,目的在于巩固基础,提高基本技能,为后续学习打好基础。
(2)灵活应用题:在基础知识上进行小综合,习题量适中,练习方式较灵活,目的是巩固所学知识并在其基础上灵活应用。
(3)综合提高题:习题量较少,有一定的难度,需要对知识进行综合应用才能完成,目的在于深化、提高和拓宽课堂所学的内容。
(四)分层评价多元化,建立自信心
对不同层次的学生采用不同的评价方法,认可不同起点学生在已有基础上取得的进步。 (下转第43页)
(上接第17页)
将分数及语言鼓励相结合对作业进行评价。一次次作业的分数提高,一次次考试成绩的提升,意味着学生运用数学知识的能力在慢慢增强,不仅如此,还可以给予学生更多的语言上的鼓励,如原本该生仅能完成第一梯度的题目,现在已能完成到第二梯度的,这就是一个大的进步,应该给予鼓励,这样就使每个学生都能从学习中尝到成功的喜悦,增强自信心。
(五)增大实验样本的范围,延长实验时间
依次在不同层次的班级开展实验,增大实验样本的范围,并适当延长实验时间。
分层作业符合新课标、因材施教与最近发展区的教育理念。“分层设计,分类评价”学生的作业,可以为每一个学生设置了天天向上、积极向上的机会,有利于各类学生的充分发展,有利于全面提高教学质量,能使学生在不同层次的作业练习中,人人学有价值的数学,人人获得必需的数学,不同学生在数学上得到不同的发展。总的来说,分层作业立足于学生的差异,关注每一位学生的发展,做到扬长避短,更好地挖掘学生内在的潜能。
(责编 卢建龙)

