混沌噪声背景下微弱脉冲信号的检测及恢复∗

苏理云 孙唤唤 王杰 阳黎明

(重庆理工大学理学院,重庆 400054)

混沌噪声背景下微弱脉冲信号的检测及恢复∗

苏理云†孙唤唤 王杰 阳黎明

(重庆理工大学理学院,重庆 400054)

(2016年11月10日收到;2016年12月23日收到修改稿)

构建了一种在混沌噪声背景下检测并恢复微弱脉冲信号的模型.首先,基于混沌信号的短期可预测性及其对微小扰动的敏感性,对观测信号进行相空间重构、建立局域线性自回归模型进行单步预测,得到预测误差,并利用假设检验方法从预测误差中检测观测信号中是否含有微弱脉冲信号.然后,对微弱脉冲信号建立单点跳跃模型,并融合局域线性自回归模型,构成双局域线性(DLL)模型,以极小化DLL模型的均方预测误差为目标进行优化,采用向后拟合算法估计模型的参数,并最终恢复出混沌噪声背景下的微弱脉冲信号.仿真实验结果表明本文所建的模型能够有效地检测并恢复出混沌噪声背景中的微弱脉冲信号.

混沌噪声,微弱脉冲信号检测,局域线性自回归模型,双局域线性模型

1 引 言

微弱信号是传统和一般的方法所不能检测到的微弱量,微弱是相对于噪声而言,不只是指信号的幅度很小,主要是指被噪声淹没的、信噪比(signal-to-noise ratio,SNR)很低的信号［1].微弱信号检测是利用电子学、信息论和概率统计等方法研究被测信号的特点,分析产生噪声的原因,检测并恢复被背景噪声淹没的微弱信号［2].检测及恢复微弱信号的传统方法主要有:时域的相关检测法、取样积分法和频域的谱分析法［3]等.然而,这些方法采用的是噪声抑制技术,检测的微弱信号的SNR需要有比较高的门限值.随着对非线性系统不断深入的研究,诸如混沌［4,5]、小波等新的理论与方法被提出,这些方法采用的是信号提取技术,为微弱信号的检测及恢复提供了新的思路.混沌噪声背景下微弱信号的检测及恢复的方法是一种基于非线性系统突变效应的新型检测方法,利用较少的数据在任意噪声背景下实现较低的SNR工作门限［6],已经成为信号处理的一个研究热点和重要分支,在通信、自动化、故障诊断和地震监测等需实时处理领域中都有很广阔的应用前景［7−12].

在通信、故障诊断、生物医学和地震监测等领域中,脉冲信号是一种典型的信号形式［13],提高噪声背景下微弱脉冲信号的检测能力、准确地测得脉冲信号,对于降低设备检测成本、为一些高精度检测仪器的开发提供理论思路、发现早期故障和增强检测系统抗干扰能力具有重要意义.为此,国内外学者对混沌噪声背景下微弱脉冲信号的检测及恢复问题进行了广泛的研究,其中包括Boxcar积分器和锁相放大器方法、Duffing-Holmes方程系统、双耦合Duffing振子系统、Birkho ff-shaw振子系统、高阶累积量法、现代互谱估计法及互高阶谱估计法［14−20]等方法,这些方法大都存在灵敏度不高、适应性不强或计算量较大的问题.为进一步提升湮没在混沌噪声中的微弱脉冲信号检测及恢复精度,近年来,很多学者应用非线性预测模型进行混沌背景下的微弱脉冲信号的检测及恢复［21−23],如把神经网络、支持向量机(SVM)［24−26]等方法应用到混沌时间序列预测模型中,虽然这些非线性方法的学习能力比较突出,但在原始数据的选择、隐含层的设计、因素的选取等方面会对预测结果产生很大的影响,存在过分依赖经验、容易陷入局部最优等缺点［27].另外,由于非线性方法不能充分利用混沌信号的性质［28,29],往往导致预测的精确性及可靠性不够高,限制了其在混沌时间序列预测方面的应用.

为了提高噪声背景下微弱脉冲信号的检测能力并降低模型的复杂程度,为故障诊断和地震监测等领域提供较精确的数据支撑,为一些高精度检测仪器的开发提供一定的理论思路,本文充分考虑了数据潜在的混沌特性和混沌系统对微弱脉冲信号的敏感性及对噪声的免疫力.基于此,首先对观测信号进行相空间重构,然后构建局域线性自回归(local linear autoregressive,LLAR)模型和双局域线性(double local linear,DLL)模型,对混沌噪声背景下的微弱脉冲信号进行检测和恢复.本文对混沌噪声背景下的微弱脉冲信号的检测及恢复的具体思路如下:首先,对观测到的信号进行相空间重构并构建LLAR模型进行单步预测,通过预测误差检测是否存在微弱脉冲信号;其次,建立混沌背景信号的DLL模型,使用向后拟合算法(back fi tting algorithm,BFA)估计模型的参数,从而恢复微弱脉冲信号.本文旨在构建能有效检测与恢复混沌背景下的微弱脉冲信号的混合模型.具体思路如图1所示.

图1 混沌噪声背景下微弱信号的检测与恢复思路Fig.1.Principle of weak signal detection and recovery from chaotic background.

本文的结构安排如下:第2部分对混沌噪声背景下的微弱脉冲信号进行检测;第3部分对混沌噪声背景下的微弱脉冲信号进行恢复检测;第4部分进行仿真实验;第5部分对本文所做工作进行总结.

2 混沌噪声背景下微弱脉冲信号的检测

2.1微弱脉冲信号的检测问题

从混沌噪声背景中检测微弱脉冲信号的问题可抽象为下面的假设检验问题:

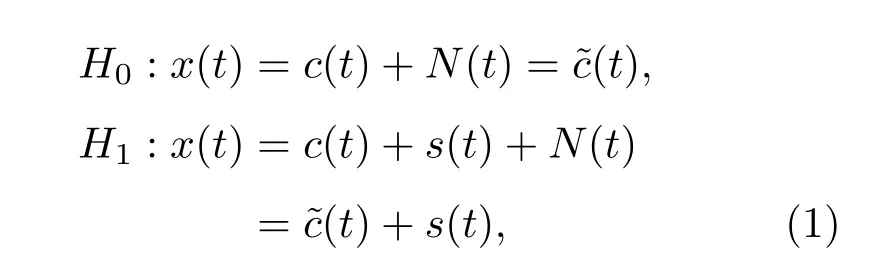
其中,x(t)表示观测信号,c(t)表示混沌噪声背景信号,s(t)表示微弱脉冲信号并且独立于混沌噪声背景信号c(t),N(t)表示均值为0的白噪声,˜c(t)表示混沌噪声背景信号c(t)与白噪声N(t)之和.

由于微弱脉冲信号s(t)淹没在混沌噪声背景信号c(t)中,若利用(1)式直接进行假设检验则无法检测出观测信号x(t)中是否含有s(t).所以首先要去除混沌噪声背景信号c(t)的干扰,把(1)式转化为如下假设检验问题:

即本部分要做的工作为:1)利用混沌背景信号这一先验知识,建立观测信号的单步预测模型,得到预测误差;2)从预测误差中检测是否存在微弱脉冲信号.

2.2 LLAR模型

对观测信号建立单步预测模型的步骤如下:第一步,对观测信号进行相空间重构;第二步,对观测信号建立LLAR模型;第三步,检验LLAR模型的优劣.

1)相空间重构

对于观测信号{x(t),t=1,2,...,n}, 其在重构相空间中的某一相点可以表示为X(t)=(x(t),x(t− τ),...,x(t− (m−1)τ))′, 其中,t=n1,n1+1,...,n;n1=1+(m−1)τ.Takens定理［30]指出,对于重构后的相空间轨迹中的每一点,存在光滑映射f:Rm→ R,使得x(t+1)=f(X(t))(t=n1,n1+1,...,n −1).如果能够求出f或者找到f的近似映射ˆf,便可对下一个数据点x(t+1)进行预测.本文采用复自相关法［31]求解延迟时间τ,采用Cao的方法［32]求解嵌入维数m.

2)LLAR模型

重构相空间之后建立观测信号x(t)的LLAR模型［33−36]来近似映射f:

其中θ(t)=(b1(t),b2(t),...,bm(t))′. 对于相空间中的任一相点(以相点XM(t)为例),其周围的q(q≤qmax,qmax=2m+1)个邻近点XM(ti)(i=1,2,...,q)具有相似的演化规律,距离越近,演化相似程度越大.本文通过计算欧氏距离d来确定这q个点,并引入高斯核函数来控制与当前相点相距较远的点在建模时造成的误差的影响.

把XM(t)的q个邻近点代入方程(4)中,于是得到一个由q个方程构成的方程组,对此方程组采用加权最小二乘法便可得到参数θ(t)的估计ˆθ(t):

其中,K(ui)为高斯核函数,通过改变窗宽h调整各个邻近点的权重.

对(5)式采用局域加权最小二乘法,得到参数θ(t)的估计:把

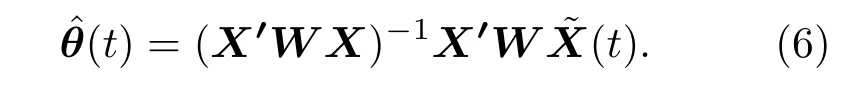
代入方程(4)中,得到单步预测值gt(X(t)),也随之得到预测误差e(t+1):

3)LLAR模型优劣性检验

2.3微弱脉冲信号的检测

根据2.2节进行假设检验判断观测信号x(t)中是否存在微弱脉冲信号s(t).用LLAR模型检测微弱脉冲信号的流程如图2所示.

图2 用LLAR模型检测微弱脉冲信号的流程图Fig.2.The fl owchart of LLAR Model.

3 混沌噪声背景下微弱脉冲信号的恢复

3.1 DLL模型

根据微弱脉冲信号的特点建立微弱脉冲信号的单点跳跃模型:

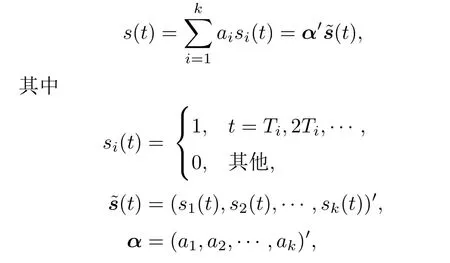
所以恢复s(t)只需要估计出α即可.

根据本文第2部分,若检测出含有微弱脉冲信号,结合微弱脉冲信号建立如下模型:

3.2DLL模型的参数估计

LLAR模型的误差平方和最小时,估计出α的值为最优值,即

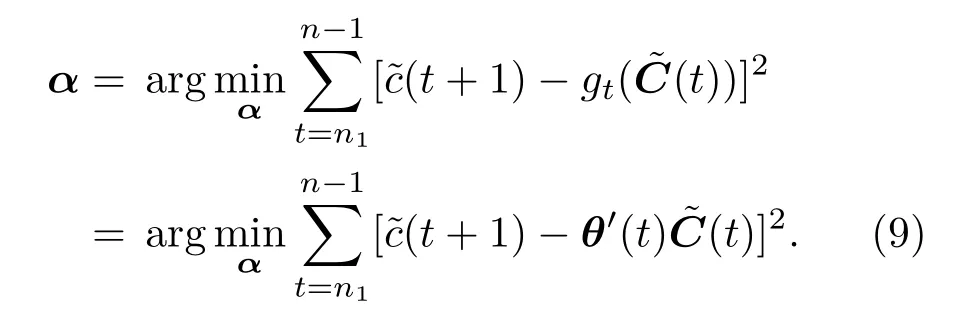
由(9)式可知,估计α的值需要已知θ(t)的值,然而,由(8)式可知估计θ(t)的值需要已知α的值.且θ(t)是时变的,α是非时变的,这里选取BFA［38]同时估计α和θ(t)的值.

采用BFA估计参数α和θ(t)的最优值的步骤如下:第一步,给定α的值估计θ(t)的值;第二步,用第一步估计出的(t)估计α的值;第三步,重复第一、二两个步骤直至得到α的最优估计.

1)给定α值估计θ(t)值(设α初值为0)

由(8)式可知,给定α时,˜c(t)是已知的.类比(5)式建立θ(t)的估计方程:

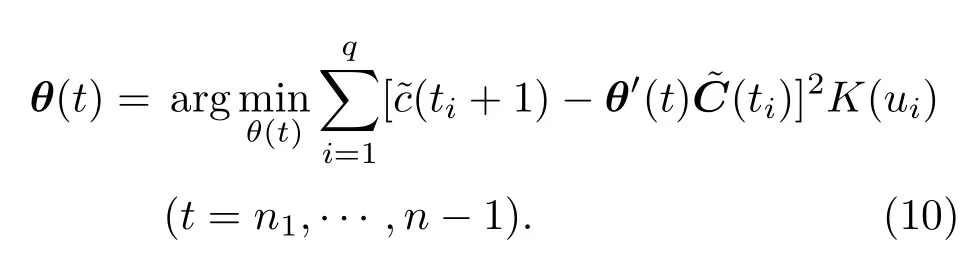
使用求解(5)式的方法求解(10)式便可求出θ(t)的估计值:

2)用1)中估计出的θ(t)值估计α的值

由(8)式可知,给定θ(t)时,gt((t))是已知的.根据(9)式可得

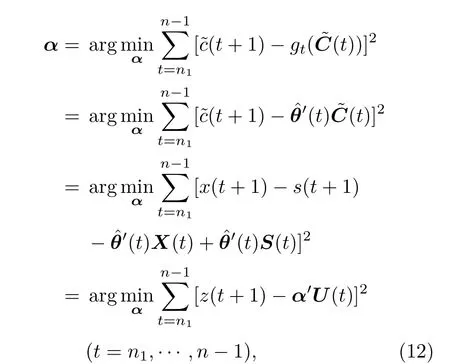
其中,

采用最小二乘法求解(12)式便可求出α的估计值:

其中U=(U(n1),U(n1+1),...,U(n −1))′,Z=(z(n1+1),z(n1+2),...,z(n))′.

3)循环1)和2)两个步骤,直到由方程(13)得到连续的两个α值相等或差距很小,这时的α值便是最优解.

3.3微弱脉冲信号的恢复

混沌噪声背景下恢复微弱脉冲信号的流程如图3所示,主要步骤如下.

1)由本文第2部分检测是否存在s(t);

2)若存在s(t),构建DLL模型以恢复s(t);

3)用BFA估计DLL模型的参数α和θ(t);

4)把估计出的α和θ(t)代入(8)式,从而恢复s(t).

注意:由于s(t)是微弱信号,很难影响相空间重构的结果,所以为了减少计算量,当对α进行迭代时,没有必要重新重构相空间和计算欧氏距离.

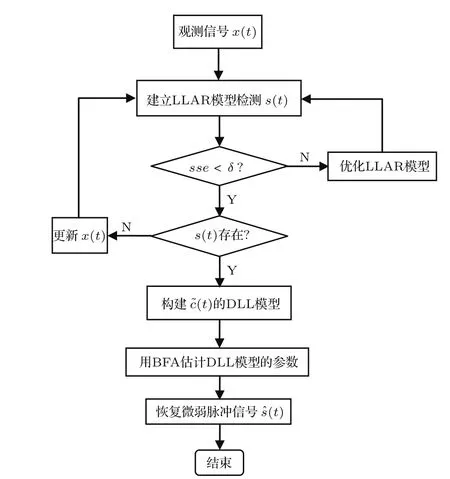
图3 恢复微弱脉冲信号的流程图Fig.3.The fl owchart of weak pulse signal recovery.

4 仿真实验结果与分析

为验证本文提出的检测模型(LLAR模型)与恢复模型(DLL模型)的可行性及有效性,进行四个仿真实验.本文实验均采用Lorenz系统生成混沌噪声背景信号,用SNR度量检测门限,用均方误差(MSE)和归一化的均方误差(NMSE)衡量恢复结果的精度.

Lorenz系统迭代方程如下:

其中η,y,z为时间函数,参数σ=10,b=8/3,r=28.假定初始条件η=1,y=1,z=1,采样时间t=0.01 s,利用四阶Runge-Kutta法产生10000个数据点,取其中的第一分量作为混沌噪声背景记为c(t).舍去前面3000个点(确保系统完全进入混沌状态),选取4000个连续序列作为混沌噪声背景,记为{c(t),t=1,2,...,4000}.采用复自相关法和Cao［32]的方法确定出x(t)的延迟时间τ=7,嵌入维数m=6.

4.1实验一:微弱脉冲信号存在性的检测实验

假设微弱脉冲信号是两个周期微弱脉冲信号的叠加信号,即s(t)=a1s1(t)+a2s2(t),其中,a1=0.15,a2=0.25,

产生长度为4000的时间序列,记为{s(t),t=1,2,...,4000},此时SNR达到−105.1382 dB.采用LLAR模型对信号进行检测,(t)和x(t)的图形和预测误差如图4所示.

图4(a)和图4(b)分别代表叠加了白噪声的混沌噪声背景信号(t)和观测信号x(t),图4(c)和图4(d)分别代表(t)单步预测的预测误差图和x(t)单步预测的预测误差图.从图4(a)和图4(b)可以看出,微弱的脉冲信号对混沌背景信号影响较弱,所以使用相同方法得到˜c(t)和x(t)的嵌入维数和延迟时间也应该是相同的.但从图4(c)和图4(d)可以看出,图4(d)中出现了明显偏大的预测误差值,意味着中可能存在微弱信号.采用2.3节的方法判断,观测信号中确实存在微弱脉冲信号,与图示结果相同.

图4信号的时间图及单步预测误差图(a)含白噪声的混沌噪声背景信号˜c(t);(b)观测信号x(t);(c)˜c(t)的预测误差图;(d)x(t)的预测误差图Fig.4.The results of example 1:(a)signal˜c(t);(b)signal x(t);(c) fi tting error of˜c(t);(d) fi tting error of x(t).

4.2实验二:微弱脉冲信号的恢复实验

由实验一的结果可知:x(t)中存在除˜c(t)之外的微弱信号,因此可以对观测信号x(t)中的微弱信号进行恢复.同样选取观测信号x(t)的4000个点作为训练样本,选取最后500个点作为预测样本.LLAR模型的误差平方和sse为0.0066,小于门限值δ=0.1,所以可以在LLAR模型基础上建立DLL模型对微弱脉冲信号进行恢复,实验结果如表1及图5所示,其中误差

表1结果表明,在时间点t处检测及恢复出的微弱脉冲信号的预测值与真实值误差较小,基本都在0.12%之下,表明DLL模型在混沌噪声背景下恢复微弱脉冲信号的性能比较好,恢复出的微弱脉冲信号精度较高.

表1 微弱脉冲信号的恢复结果Table 1.The results of example 2.

图5显示的是微弱脉冲信号的检测及恢复结果,为了便于观察,图5(a)中预测值向右平移了10个单位,此时SNR达到−105.1382 dB.由表2及图5的结果可以看出:微弱脉冲信号s(t)的真实值与预测值的拟合效果很好,而且在进行几次迭代后,预测结果的NMSE近似为5.21×10−7,MSE近似为8.89×10−10.

图5 微弱脉冲信号的检测及恢复结果 (a)仿真结果对比图;(b)微弱脉冲信号的NMSE;(c)微弱脉冲信号的MSEFig.5.The results of weak pulse signal estimation:(a)Simulation results;(b)NMSE of s(t);(c)MSE of s(t).

4.3实验三:不同强度脉冲信号的检测及恢复实验

假设微弱脉冲信号s(t)的周期不变,通过改变a1,a2的数量级的大小控制微弱脉冲信号s(t)的强度,即a1=1.5×10j,a2=2.5×10j(j=−5,−4,−3,−2,−1,0,1). 同样选取观测信号x(t)的4000个点作为训练样本,选取最后500个点作为预测样本,采用LLAR模型对信号进行检测,采用DLL模型进行信号恢复.实验结果如表2所列.

由表2显示的结果可以看出,随着脉冲信号强度的逐渐变化,DLL模型恢复信号的能力也发生了改变.SNR大于−58 dB的时候,尽管NMSE的值比较小,但MSE的值比较大,所以恢复微弱信号的效果不理想;同样,在SNR小于−242 dB时,NMSE的值明显增大,此时DLL模型恢复微弱信号的能力极弱,这是因为脉冲信号太强会破坏混沌噪声背景信号的几何结构,脉冲信号太弱就会被混沌噪声背景信号中的一些分量模糊掉.所以SNR在−104.8076 dB到−196.9111 dB之间时,DLL模型恢复微弱信号的效果比较优异,此时NMSE和MSE均比较小,由此也可以看出,DLL模型检测微弱信号的SNR门限值较低.

表2 不同强度脉冲信号的恢复结果Table 2.Di ff erent intensity of pulse signal detection and estimation.

4.4实验四:不同模型的性能比较

为判断模型检测及恢复微弱脉冲信号的效果的优劣,与文献[22]中的对偶约束最小二乘支持向量机(LS-SVM)模型、遗传算法-支持向量机(GASVM)模型、LS-SVM模型及径向基函数(RBF)神经网络模型进行比较,选取

分别采用复自相关法和Cao［32]的方法确定x(t)的延迟时间τ=1,嵌入维数m=6.使用LLAR模型进行信号检测,使用DLL模型进行信号恢复,采用SNR及均方根误差判断模型的优劣,结果如图6和表3所示.

表3 不同模型的性能比较Table 3.The performance comparison of di ff erent models.

图6 (网刊彩色)单脉冲信号的检测及恢复实验 (a)仿真结果对比图;(b)微弱脉冲信号的MSE;(c)微弱脉冲信号的NMSE;(d)微弱脉冲信号的RMSEFig.6.(color online)The results of single weak pulse signal estimation:(a)Simulation results;(b)MSE of s(t);(c)NMSE of s(t);(d)RMSE of s(t).

由图6和表3可知,微弱脉冲信号的估计值为0.006015,NMSE为2.402× 10−6,RMSE为1.72× 10−6,此时SNR达到−188.545 dB,与文献[22]中实验1的模型得到的结果相比,本文模型的优势更加明显,本文模型得到的RMSE值的数量级为10−6,比用其他模型得到的RMSE值至少提高了2个数量级,且SNR值远远低于其他模型的SNR值,具体结果见表3.这些足以表明DLL模型的检测能力更强,恢复效果更好.

5 结 论

结合混沌时间序列的短期可预测性和对微小扰动的敏感性,结合相空间重构构建了LLAR模型和DLL模型.本文所建模型不需要知道混沌系统动力学方程和脉冲信号的先验知识,可以在非线性映射未知的情况下,对混沌噪声背景下的微弱脉冲信号进行检测和恢复,是一种简单且易于理解和应用的检测与恢复微弱信号的模型.从实验结果可得出如下结论:LLAR模型能够有效地从混沌噪声背景下检测出微弱脉冲信号;使用DLL模型恢复出的微弱脉冲信号精度高,预测值与真实值之间的误差基本都在0.12%之下,并且MSE低至8.89×10−10,RMSE低至5.21×10−7;从不同强度脉冲信号的检测与恢复实验中可以看出,本文构建的模型能利用较少的数据在混沌噪声背景下实现较低的SNR工作门限并且预测精度保持在较高的水平,即SNR低至−196.9111 dB时RMSE可低至1.98×10−3;与其他模型比较的结果更直观地显示出本文构建的模型检测能力更强,恢复效果更好.下一步将继续完善LLAR模型的预测误差对构建检测及恢复模型的影响,以期实现更低的SNR工作门限,并推广到其他微弱信号的检测及恢复领域.

[1]Cai Z Q 2014M.S.Thesis(Baotou:Inner Mongolia University of Science&Technology)(in Chinese)[蔡志全2014硕士学位论文(包头:内蒙古科技大学)]

[2]Zhang K L,Zhu H M 2009Avionics Technol.40 30(in Chinese)[章克来,朱海明2009航空电子技术40 30]

[3]Xia J Z,Liu Y H,Leng Y G,Ge J T 2011Noise Vib.Control.31 156(in Chinese)[夏均忠,刘远宏,冷永刚,葛纪桃2011噪声与振动控制31 156]

[4]Lü J H,Lu J A,Chen S H 2002Chaotic Time Series Analysis and Application(Wuhan:Wuhan University Press)p8(in Chinese)[吕金虎,陆君安,陈士华 2002混沌时间序列分析及其应用(武汉:武汉大学出版社)第8页]

[5]Su L Y,Li C L 2015Discrete Dyn.Nat.Soc.2015 329487

[6]Wang D S,Chen L,Shi Y D 2010J.Dyn.Control8 48(in Chinese)[王德石,谌龙,史跃东 2010动力学与控制学报8 48]

[7]Su L Y 2010Comput.Math.Appl.59 737

[8]Wang X L,Wang W B 2015Chin.Phys.B24 080203

[9]Lu P,Li Y 2005Acta Electron.Sin.33 527(in Chinese)[路鹏,李月 2005电子学报 33 527]

[10]Su L Y,Ma Y J,Li J J 2012Chin.Phys.B21 020508

[11]Li M P,Xu X M,Yang B C,Ding J F 2015Chin.Phys.B24 060504

[12]He G T,Luo M K 2012Chin.Phys.Lett.29 060204

[13]Liu L S,Zhang L 2009Electron.Test8 19(in Chinese)[刘连生,张磊2009电子测试8 19]

[14]Li Y,Yang B J,Du L Z,Yuan Y 2003J.Electron.Infor.Technol.25 195(in Chinese)[李月,杨宝俊,杜立志,袁野2003电子与信息学报25 195]

[15]Dai Y S 1994Weak Signal Detection Method and Instrument(Beijing:National Defend Industry Press)pp268–275(in Chinese)[戴逸松 1994微弱信号检测方法及仪器(北京:国防工业出版社)第268—275页]

[16]Li Y,Lu P,Yang B J 2006Acta Phys.Sin.55 1672(in Chinese)[李月,路鹏,杨宝俊 2006物理学报55 1672]

[17]Swami A,Mendel J M 1988Cumulant-based Approach to the Harmonic Retrieval ProblemNew York,USA,April 11–14,1988 pp2264–2267

[18]Chang N N,Lu C H,Liu C 2006J.Electron.Meas.Instrum.20 86(in Chinese)[苌凝凝,鲁昌华,刘春2006电子测量与仪器学报20 86]

[19]Li J Y 2010M.S.Thesis(Chengdu:University of Electronic Science and Technology of China)(in Chinese)[李继永2010硕士学位论文(成都:电子科技大学)]

[20]Ma Y,Shi Y W,Kang X T 2002Acta Electron.Sin.30 14(in Chinese)[马彦,石要武,康小涛 2002电子学报 30 14]

[21]Xing H Y,Zhang Q,Xu W 2015Acta Phys.Sin.64 040506(in Chinese)[行鸿彦,张强,徐伟 2015物理学报64 040506]

[22]Xing H Y,Zhu Q Q,Xu W 2014Acta Phys.Sin.63 100505(in Chinese)[行鸿彦,朱清清,徐伟2014物理学报63 100505]

[23]Zhu Z W,Leung H 2002IEEE Trans.Circ.Sys.I49 170

[24]Ma J W,Qing C Y 2013Sig.Process.29 1609(in Chinese)[马尽文,青慈阳 2013信号处理 29 1609]

[25]Zhang Q,Xing H Y 2015Acta Electron.Sin.43 901(in Chinese)[张强,行鸿彦 2015电子学报 43 901]

[26]Liu H,Liu D,Li Q 2005J.Sys.Sci.Infor.25 94(in Chinese)[刘涵,刘丁,李琦 2005系统工程理论与实践 25 94]

[27]Zheng H L,Xing H Y,Xu W 2015Sig.Process.31 336(in Chinese)[郑红利,行鸿彦,徐伟2015信号处理31 336]

[28]Leung H 2014ChaoticSignalProcessing(Beijing:Higher Education Press)pp110–113

[29]Li Y,Yang B J,Deng X Y,Lin H B 2005J.Electro.Infor.Technol.27 731(in Chinese)[李月,杨宝俊,邓小英,林红波2005电子与信息学报27 731]

[30]Takens F 1981Lecture Notes Math.898 366

[31]Lin J Y,Wang Y K,Huang Z P 1999Sig.Process.15 220(in Chinese)[林嘉宇,王跃科,黄芝平 1999信号处理15 220]

[32]Cao L Y 1997Physica D110 43

[33]Peng X W,Su L Y,Li C L,Yin Y,Sun H H 2015Stat.Appl.4 56(in Chinese)[彭相武,苏理云,李晨龙,殷勇,孙唤唤2015统计学与应用4 56]

[34]Su L Y,Li C L 2015Math.Problems Eng.2015 901807

[35]Li C L 2015M.S.Thesis(Chongqing:Chongqing University of Technology)(in Chinese)[李晨龙 2015硕士学位论文(重庆:重庆理工大学)]

[36]Li C,Su L 2017Mech.Syst.Sig.Proc.84 499

[37]She D,Yang X 2010Math.Problems Eng.2010 205438

[38]Fan J,Yao Q,Cai Z 2003J.Royal Stat.Soc.65 57

PACS:05.45.Pq,05.45.Tp,05.45.Gg,02.50.–rDOI:10.7498/aps.66.090503

Detection and estimation of weak pulse signal in chaotic background noise∗

Su Li-Yun†Sun Huan-Huan Wang Jie Yang Li-Ming

(School of Science,Chongqing University of Technology,Chongqing 400054,China)

10 November 2016;revised manuscript

23 December 2016)

As is well known,people has been su ff ering noise interference for a long time,and more and more researches show that a lot of weak signals such as pulse signal are embedded in the strong chaotic noise.The purpose of weak signal detection and recovery is to retrieve useful signal from strong noise.It is very difficult to detect and estimate the weak pulse signal which is mixed in the chaotic background interference.Therefore,the detection and recovery of weak signal are signi fi cant and have application value in signal processing area,especially for the weak pulse signal detection and recovery.By studying various methods of detecting and estimating the weak pulse signal in strong chaotic background noise,in this paper,we propose an efficient hybrid processing technique.First,based on the short-term predictability and sensitivity to the tiny disturbance,a new method is proposed,which can be used for detecting and estimating the weak pulse signals in chaotic background that the nonlinear mapping is unknown.We reconstruct a phase space according to Takens delay embedding theorem;then we establish the local linear autoregressive model to predict the short-term chaotic signal and obtain the fi tting error,and judge whether there are weak pulse signals.Second,we establish a single-jump model for pulse signals,and combine the local linear autoregressive model with it to build a double local linear(DLL)model for estimating the weak pulse signal.DLL model contains two parameters,and the two parameters a ff ect each other.We use the back- fi tting algorithm to estimate model parameters and ultimately recover the weak pulse signals.Detecting and estimating the pulse signals in chaotic background turns into estimating the parameters of DLL model.The minimum fi tting error criterion is used as the objective function to estimate the parameters of the DLL model.To make the estimation more exact,we can use the formula of mean square error.The new algorithm presented here in this paper does not need to know the prior knowledge of the chaotic background nor weak pulse signal,and this algorithm is also simple and e ff ective.Finally,the simulation results show that the method is e ff ective for detecting and estimating the weak pulse signals based on the chaotic background noise.Speci fi cally,the weak pulse signal can be extracted well with low SNR and the minimum mean square error or the minimum normalized mean squared error is very low.

chaotic noise,weak pulse signal detection,local linear autoregressive model,double local linear model

10.7498/aps.66.090503

∗国家自然科学基金(批准号:11471060)和重庆市科委基础与前沿研究计划项目(批准号:cstc2014jcyjA40003)资助的课题.

†通信作者.E-mail:cloudhopping@163.com

*Project supported by the National Natural Science Foundation of China(Grant No.11471060)and the Fundamental and Advanced Research Project of CQ CSTC of China(Grant No.cstc2014jcyjA40003).

†Corresponding author.E-mail:cloudhopping@163.com