计算相位响应曲线的方波扰动直接算法∗

谢勇程建慧

(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,西安 710049)

计算相位响应曲线的方波扰动直接算法∗

谢勇†程建慧

(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,西安 710049)

(2016年11月25日收到;2017年1月6日收到修改稿)

通过相位响应曲线可对具有极限环周期运动的动力系统的性质有更为深入的理解.神经元是一个典型的动力系统,因此相位响应曲线提供了一种研究神经元重复周期放电行为的新思路.本文提出一种求解相位响应曲线的方法,即方波扰动的直接算法,通过Hodgkin-Huxley,FitzHugh-Nagumo,Morris-Lecar和Hindmarsh-Rose神经元模型验证该算法可计算周期峰放电、周期簇放电的相位响应曲线.该算法克服了其他算法在运用过程中的局限性.利用该算法计算结果表明:周期峰放电的相位响应曲线类型是由其分岔类型所决定;在Morris-Lecar模型中发现一种开始于Hopf分岔终止于鞍点同宿轨道分岔的阈上周期振荡,其相位响应曲线属于第二类型.通过大量的相位响应曲线的计算发现相位响应的相对大小及正负性仅取决于扰动所施加的时间,而且周期簇放电的相位响应曲线比周期峰放电的相位响应曲线更为复杂.

相位响应曲线,峰放电,簇放电,分岔

1 引 言

神经元和神经元所组成的神经系统具有高度复杂的动力学行为,呈现明显的非线性现象,因此从非线性动力学角度研究和理解神经元和神经系统的行为规律是十分必要的.其研究的一般思路是建立动力学模型,然后利用动力学系统理论解读神经元和神经系统活动规律及其动力学机理.在神经元建模方面,英国生理学家Hodgkin和Huxley［1]建立了Hodgkin-Huxley(HH)模型,它能很好地描述枪乌贼的神经元峰放电(spiking)行为.这一开创性工作成为定量研究可兴奋生物细胞电生理特性的里程碑.为了便于理论分析,在1961年和1962年,FitzHugh和Nagumo等分别独立地导出了一个由多项式表达的二维FitzHugh-Nagumo(FHN)模型［2,3].该模型尽管形式非常简洁,却抓住了神经元兴奋的本质特征.1981年,Morris和Lecar［4]结合HH模型和FHN模型各自的优点提出了一个描述藤壶(一种甲壳纲的小动物)肌肉纤维电生理特征的二维Morris-Lecar(ML)模型,现在也被作为神经元模型而广泛引用.随后,Hindmarsh和Rose［5]为了解释“尾电流反转(tail current reversal)”现象提出了Hindmarsh-Rose(HR)模型.HR模型可以呈现峰放电和簇放电(bursting)行为.目前针对不同生物和不同类型的神经元已经建立了大量的模型［6].有了神经元模型,接下来就可以通过非线性动力学理论分析神经元复杂而丰富的放电行为,并揭示其发生的动力学机理.已有大量的理论或数值分析确定神经元模型中分岔、混沌和分形等非线性现象［7−17].噪声无处不在,对随机共振现象的研究表明噪声可能增强神经元、神经元网络以及神经系统检测微弱信号的能力［18−22].

通过对神经元模型的数值计算很容易再现神经元各种复杂的放电模式,比如周期峰放电、周期簇放电、混沌峰放电、混沌簇放电和整数倍放电等.本文主要关注周期峰放电和周期簇放电两种放电模式.这两种放电模式从非线性动力学角度讲都是极限环振子,而描述极限环的最简单的方式就是采用振子的相位.通过相位变换就可以把复杂的状态空间模型映射到一维的相位模型,这样有助于获得振子系统的解析解.处于极限环运动状态的振子系统对外界刺激的响应特征可以通过相位响应曲线(phase response curve,PRC)进行刻画［23,24],相位响应曲线有时也称为相位重置曲线(phase resetting curve,PRC).PRC是一个关于相位的函数,它是指极限环振子在不同相位处由外界扰动引起振荡周期的暂态变化.

PRC是由文献[25,26]在研究生物节律的重置过程中引入的,在很多方面都有极其重要的作用,随后被应用到神经元系统中.在相空间中PRC表示扰动后周期振子相位的提前或滞后.如果周期振子的周期缩短了,则称为相位提前(phase advance);相反,如果周期变长了,则称为相位滞后(phase delay).在研究生物节律时,PRC已成为研究的标准工具.比如人体对光刺激的PRC是调整睡眠时间疗法的理论基础.在心脏病学中,PRC可用来理解各种心律失常的发生［27,28].在神经科学中,相位简化模型可用来简化复杂的神经科学的生物模型［29−31].如果知道一个振子系统的PRC,就可以很容易地预测该振子在受到外界刺激时的行为.另外,PRC可用来预测周期刺激的拖带(entrainment)以及耦合振子的相锁(phase locking),还可以用来理解相干振荡器、行波(traveling waves)等动力学行为.耦合神经元的相互作用函数可以通过PRC数值计算得到［32].文献[33]详细介绍了神经科学中PRC及其应用.已有的研究表明周期峰放电的神经元的PRC可分为两大类［23]:第一类型PRC是指PRC取值全为正或者全为负,这样兴奋性扰动将导致峰放电提前或者滞后;而第二类型PRC是指PRC取值是两相的,部分为正,部分为负,这样将导致当扰动施加在不同的相位处时,部分相位处将引起放电提前,而部分相位处引起放电滞后.

而PRC的类型与神经元从静息到周期峰放电所跨越的分岔类型密切相关.具体地讲,具有第一类型PRC的神经元跨越了不变圆上的鞍结分岔(saddle-node on invariant circle bifurcation,SNIC),而具有第二类型PRC的神经元则经历了Hopf分岔.因此PRC的类型与神经元的兴奋性类型一一对应.

周期簇放电的PRC与周期峰放电的PRC定义类似,是指簇放电神经元在受到外界扰动时下一个簇到来时刻与未扰动的簇之间的相位差.对于周期簇放电的PRC与其分岔类型之间的关系,现在的研究还比较少,它们之间的关系还不清楚.不过,要弄清这一关系的前提就是首先要计算获得周期簇放电的PRC.

PRC可通过实验或理论分析得到.在进行理论分析时,需要知道动力系统具体的表达式.对于一些简单的模型,其PRC可通过相位简化方法得到其解析解;但对复杂的、非线性的神经元模型,往往无法解析求解,因此有必要通过数值计算得到其PRC.目前计算PRC的基本思路有两种［32]:一种是根据PRC的定义,即用神经元振子对短的脉冲刺激的响应直接计算,该思路比较简单,但扰动是有限幅值扰动,导致计算结果不是很精确;另一种是将神经元振子在极限环附近线性化,求解线性伴随方程,然而求解伴随方程需要向后积分且不稳定,因此该算法并不简单.不过该算法是一些软件求解PRC的依据,比如XPPAUT［34]和MatCont［35].对于前一种思路所对应的直接算法中,通常在膜电位上施加典型的峰扰动,这一典型峰是取自簇放电本身的一个尖峰,该扰动形式更接近实际的生理过程.但该方法是针对簇放电的,而且典型的峰扰动所需确定的参数较多,比如对于HR模型,需要确定5个参数,方程增加一维,计算费时［36].无限小扰动的改进算法也是直接算法的一种［37],该算法计算速度快.但该算法本质在于求解特征矩阵,在计算簇放电神经元模型的PRC时,容易溢出,出现错误.例如该算法应用于Chay模型和Wang模型时,就出现了溢出错误.因此基于上述算法的局限性,本文提出了一种基于PRC定义的直接算法,以方波扰动作为扰动形式,该算法可适用于峰放电和簇放电.

本文内容安排如下:第2部分首先介绍我们的直接算法,通过HH模型验证该算法的可行性,然后将该算法运用到FHN模型中,揭示FHN神经元的PRC类型;第3部分利用本文的直接算法通过ML模型探究周期峰放电模型的PRC的表现特征,揭示分岔机理与PRC类型之间的关系;第4部分通过HR模型验证该算法同样适用于计算周期簇放电的PRC;第5部分是结论.

2 PRC的直接算法及算例

2.1 方波扰动的直接算法

对一个自治动力系统,其模型可定义为

其中,X=(x1,x2,...,xN)为N 维相空间的状态变量.记该系统的解为X(t)=Ψ(X0,t),其中X0=X(0)是初始值.假定该系统存在一个稳定的极限环,其周期为T.在极限环上选取一点作为初始点,即,则可得到一个沿着极限环移动的周期为T的迹线,即.而位于极限环上的一点的相位可以由两种不同的方式进行定义:一种是空间相位,按照极限环的长度均匀增加进行度量;另一种以一状态变量沿着极限环时间均匀增加进行度量.根据相位简化方法,本文采用后一种定义,因为该定义可得到一个简单的相位公式.如果认为极限环上的初始点相位为0,则极限环上其他点的相位为

对系统在极限环上一点x0处施加一扰动ˆF,若该扰动仅使得该点沿极限环偏移,则该扰动的作用仅是增加或减少动力系统的周期,或者说延迟或提前扰动后的迹线回到点x0处的时间,则该点的相位响应为

其中t0为未加扰动从点x0处出发第一次回到点x0处的时间,0为扰动后第一次回到x0处的时间,为扰动后的周期.PR表示相位响应(phase response).

小幅值的扰动ˆF通常用来模拟一个瞬时的增加或减小后突触神经元的电流作用,而忽略关于离子通道参数的影响.在计算此类扰动的PRC时,先数值积分未扰动的系统F到施加扰动相位(或时刻),再积分扰动后的系统,积分区间长度为扰动持续的时间长度,然后继续数值积分原系统F,最后相位响应根据(3)式求解,则PRC由施加在[0,1)区间上的扰动所对应的相位响应构成.这就是本文计算PRC的直接算法.在计算PRC过程时,常常假定扰动后的迹线会在一次放电环后回到极限环周期轨道上,并以下一次放电环上的参考相位(周期峰放电一般选取膜电位最高的尖峰时刻)来测量相位响应.此外还需要注意的是,选取未扰动的极限环轨道上的一点作为参考点表明开始时间,记为t=0,相位θ=0.本文中的扰动为方波扰动,其扰动幅值为Ip,持续时间为tp,即在扰动持续时间tp内扰动幅值保持常数Ip,因此称为方波扰动.该扰动施加在表示神经元膜电位变化的微分方程右端项上,对有生理意义的神经元模型而言,可以表示为,其中C为膜电容.记膜电位在受到外界扰动时的PRC为PRC1,由于本文后面的计算都是在膜电位上施加外界扰动,因此我们用PRC来表示PRC1,不再进行区分.关于方波扰动的参数Ip,tp的选择,对周期峰放电而言,Ip的大小取决于膜电位的变化幅值以及模型中外加电流的大小(若存在),可取膜电位幅值或者外加电流大小的1/20—1/5;tp的值取决于周期的大小,并且尽量持续时间较短,一般情况下选取不超过峰放电的脉冲宽度.对周期簇放电而言,tp的值一般不超过簇内一个尖峰动作电位的持续时间;Ip的取值类似周期峰放电,但对于周期簇放电,要注意在扰动作用下簇内的尖峰个数不能发生变化.具体的算法实现过程为:

1)计算神经元周期峰放电或周期簇放电所对应的极限环及其周期,记周期为T0,对神经元系统进行时间尺度变换,将周期变换为1,可参考文献[37];

2)在极限环上选取参考相位,记为t0(对周期峰放电,一般选取膜电位最大的时刻作为参考相位;对周期簇放电,一般选择第一个尖峰膜电位最大的时刻作为参考相位);

3)将极限环按时间等间距分为n个区间,n=1/tp,在不存在扰动时,按未扰动系统数值积分,在存在扰动的[(m−1)tp,mtp]时间范围内,按扰动系统数值积分,其中1≤m≤n;记录第一次回到参考相位的时间,记为0;根据(3)式计算每个节点处的PRC值,若大于0则为相位提前,若小于0表示相位滞后.

2.2 HH神经元模型周期峰放电的PRC

为了与现有的文献计算结果比较来说明本文提出的直接算法的正确性,特意选择文献[37]中的HH神经元模型算例.HH神经元模型的具体形式如下:

其中V为膜电位;C为膜电容;m,h为Na离子通道的门控变量;n为K离子通道的门控变量;gK,gNa和gL分别为K离子通道、Na离子通道和漏电流的最大电导;VK,VNa和VL分别为它们各自的反转电位;Iapp为外加电流强度.an(V),bn(V),am(V),bm(V),ah(V)和bh(V)满足:

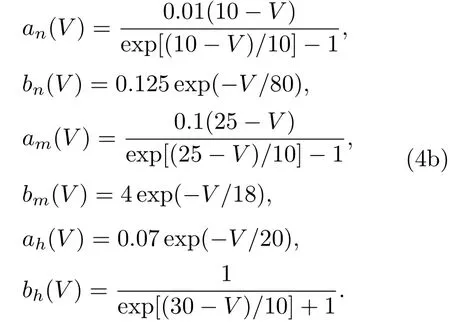
选取参数

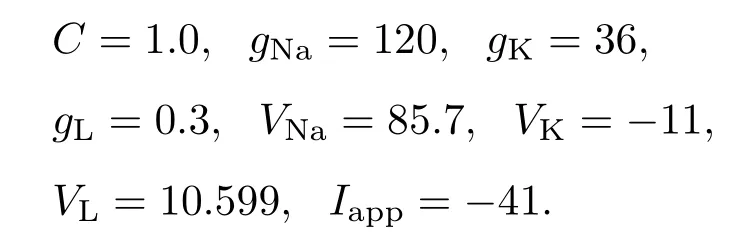
其中电导单位为mS/cm2,电压单位为mV,电容单位为µF/cm2,电流单位为µA/cm2.

在上述参数取值条件下HH模型存在两个稳定的极限环,分别称为外极限环和内极限环.本文所取初始条件分别为(5.25,0.07,0.60,0.011)和(7.25,0.17,0.13,0.55),如图1所示.

通过分岔软件XPPAUT对HH模型做膜电位关于外加电流强度的分岔分析,发现有两个区间存在两个稳定极限环共存的情形,它们分别是[34.95,38.51]和[40.01,41.28],如图2所示.图2(b)是图2(a)的局部放大.图中粗实线表示稳定平衡态,点划线表示不稳定平衡态,细实线表示稳定极限环的振荡最大和最小值,而点线表示不稳定极限环的振荡最大和最小值(本文中所有分岔图都采用这种表达方式).HB表示Hopf分岔;FLC表示极限环折叠分岔(fold limit cycle bifurcation),有时也叫极限环鞍结分岔(saddle-node bifurcation of limit cycles).可以看出图1中两个共存的极限环正是在第二狭窄区间里取Iapp=41获得的.

图1 HH神经元模型两个共存的稳定极限环在(V,m)相平面上的投影Fig.1.The(V,m)projections of two coexisting stable limit cycles of the HH neuron model.

接下来运用本文的直接算法计算HH模型内、外极限环的PRC.对内极限环所施加的扰动为Ip=10,tp=0.004,计算步长为0.001(周期归一化为1,以下同此做法);对外极限环所施加的扰动为Ip=5,tp=0.004,计算步长为0.0001.这样HH神经元模型的内、外极限环的PRC如图3所示.我们的计算结果与文献[30]的结果除了幅值不同以外几乎完全一致,事实上,PRC相对值才具有意义.值得注意的是,由于在极限环上所取的初始参考点不一样造成PRC开始的位置不同,但波动顺序是完全一致的,从而说明本文的算法是可信的.

由图3可知,无论内极限环还是外极限环,HH神经元模型的PRC值既有正值又有负值,这表明HH神经元模型的PRC为第二类型PRC.由前面的分岔分析可知HH神经元模型从静息到放电的确经历了一个次临界Hopf分岔.

图2 HH神经元模型膜电位对外加电流强度的分岔图Fig.2.Bifurcation diagram of the membrane potential V versus the strength of the applied current Iappin the HH neuron model.

图3 (a)内极限环的PRC;(b)外极限环的PRCFig.3.(a)The PRC of the inner limit cycle;(b)the PRC of the outer limit cycle.

2.3 FHN神经元模型周期峰放电的PRC

FHN神经元模型的放电行为和分岔机理都有相关的研究,但是对其PRC的计算还较为少见,因此本文采用方波扰动的直接算法计算其PRC.FHN神经元模型的形式如下［2,3]:

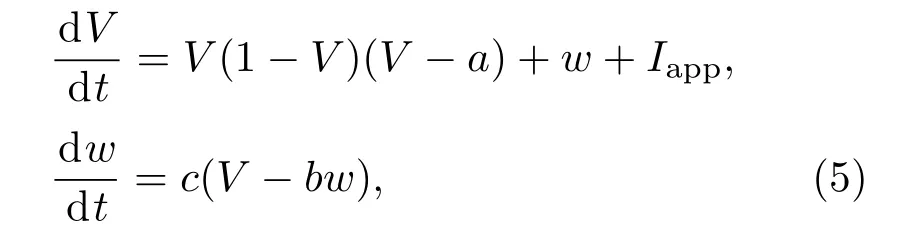
其中V表示膜电位;w表示恢复变量;a,b,c为系统参数;Iapp为外加电流强度.FHN模型是一个无量纲的神经元模型.

取参数a=0.139,b=2.54,c=0.008,分析FHN神经元模型随外加电流强度的分岔机理,如图4所示.

由图4可知,当I=0.03469时,神经元经历一个次临界Hopf分岔由静息态变为周期峰放电;当I=0.1509时,经历另外一个次临界Hopf点,由周期峰放电变为静息态.运用直接算法计算该模型的PRC,所施加扰动Ip=0.002,tp=0.004,计算步长为0.001,其放电模式与PRC的对应关系如图5所示.

图4 FHN神经元模型的分岔图Fig.4.Bifurcation diagram of the membrane potential versus the applied current strength in the FHN neuron model.

图5 FHN神经元模型的放电形式及其对应的PRCFig.5.Periodic spiking and its corresponding PRC in the FHN neuron model.

从图5可以看到FHN神经元模型的PRC取值有正有负,表现为第二类型的PRC.这与神经元所经历的Hopf分岔密切相关.而且PRC的幅值最大值并不与神经元放电的尖峰时刻存在对应关系,而是取值取决于扰动所施加的时间.同时还可以看到PRC在前半周期取值几乎接近于0,在后半周期才出现明显的变化.这是由于在放电尖峰附近对外部扰动不敏感,而随之出现的超极化区域所占时间又较长,因此导致了较长区域的PRC取值几乎为0.

3 ML模型的PRC

由于ML模型在不同参数条件下随外加电流强度有着不同的分岔行为,因此计算ML模型的PRC能更充分地揭示分岔与PRC形状的关系.ML模型有三种电流,即钾电流、钙电流和漏电流,具体形式为［4]

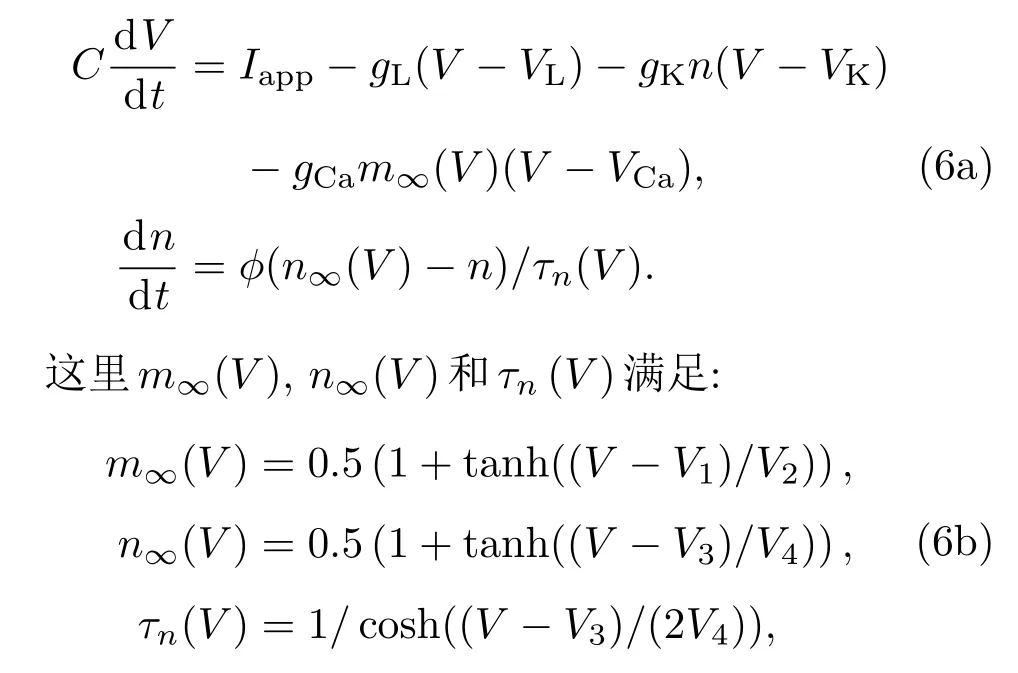
其中V表示膜电位变量;n为恢复变量;C为膜电容;V1,V2,V3和V4为拟合电压膜片钳数据的参数;ϕ为快慢时间尺度比率;gCa,gK和gL分别为Ca离子通道、K离子通道和漏电流的最大电导;VCa,VK和VL分别为它们各自的反转电位;Iapp为外加电流强度.其中电导率单位为mS/cm2,电压单位为mV,电容单位为µF/cm2,电流单位为µA/cm2.

尽管ML模型是一个简单的、只含有两个变量的动力系统,然而在不同的参数集下却可以表现出丰富的放电行为［35,38].本文选取如下三组参数研究ML模型的动力学特性,如表1所列.

表1 ML模型的参数集Table 1.Parameter sets of the ML model.

在上述三组参数条件下计算了ML模型随外加电流强度变化的分岔行为.在第一组参数条件下,ML模型从静息态到周期峰放电在Iapp=38.76处经历了一个SNIC,呈现第一类型兴奋性,如图6(a)所示.图6(b)是在第二组参数条件下,ML从静息态到周期峰放电在Iapp=45.47处经历了一个次临界Hopf分岔,呈现第二类型兴奋性.特别地,在第三组参数条件下,随着外加电流强度逐渐增大,ML模型在Iapp=39.96处静息态通过一个平衡点的鞍结分岔消失,跳到一个由次临界Hopf分岔而来的极限环上,呈现一个阈上的周期振荡.这个极限环随着外加电流强度逐渐减小,在Iapp=35.01处终止一个鞍点同宿轨道分岔(saddle homoclinic orbit bifurcation),如图6(c)所示.从图6(c)还可以看到存在一个由两条竖直的短划线所夹的狭窄区间,在此区间内,ML模型有两个稳定的平衡态和一个稳定的极限环,呈现三稳态.左边的短划线位于次临界Hopf分岔处,而右边的短划线位于平衡点鞍结分岔处.

针对这三组参数,取外加电流强度Iapp分别为39,45和39,可以发现前面两种情形ML模型呈现周期峰放电,如图7(a)和图7(b)所示;而最后一种情形则表现为阈上周期振荡,如图7(c)所示.

图6 ML模型在不同参数条件的分岔图 (a)第一组参数;(b)第二组参数;(c)第三组参数Fig.6.Bifurcation diagrams of the membrane potential versus the applied current strength in the ML neuron model with di ff erent parameter sets:(a)The fi rst parameter set;(b)the second parameter set;(c)the third parameter set.

图7 ML模型在不同参数条件的放电模式 (a)在第一组参数下当Iapp=39时ML模型的周期峰放电;(b)在第二组参数条件下,当Iapp=45时ML模型的周期峰放电;(c)在第三组参数条件下,当Iapp=39时ML模型的阈上周期振荡Fig.7.Firing patterns of the ML neuron model with di ff erent parameter sets:(a)Periodic spiking with the fi rst parameter set when Iapp=39;(b)periodic spiking with the second parameter set when Iapp=45;(c)suprathreshold periodic oscillation with the third parameter set when Iapp=39.

运用直接算法计算ML模型在前面三组参数条件下当Iapp分别等于39,45和39时的PRC.在第一组参数条件下,当Iapp=39时所施加扰动为Ip=20,tp=0.004,计算步长为0.001,PRC如图8(a)所示.在第二组参数条件下,当Iapp=45时所施加扰动为Ip=30,tp=0.004,计算步长为0.001,PRC如图8(b)所示.图8(c)所示的PRC为在第三组参数条件下当Iapp=39时的结果,此时所施加扰动为Ip=−10,tp=0.005,计算步长为0.001.

图8 (a)在第一组参数下当Iapp=39时ML模型的周期峰放电及其对应的PRC;(b)在第二组参数条件下当Iapp=45时ML模型的周期峰放电及其对应的PRC;(c)在第三组参数条件下当Iapp=39时ML模型的阈上周期振荡及其对应的PRCFig.8.Periodic oscillations and their corresponding PRCs in the ML neuron model with di ff erent parameter sets:(a)Periodic spiking and its corresponding PRC with the fi rst parameter set when Iapp=39;(b)periodic spiking and its corresponding PRC with the second parameter set when Iapp=45;(c)suprathreshold periodic oscillation and its corresponding PRC with the third parameter set when Iapp=39.

由ML模型的PRC计算结果可知,如果从静息态到周期峰放电经历SNLC分岔,则属于第一类型兴奋性,其PRC的类型确为第一类型,PRC取值几乎全部为正.当从静息态到周期峰放电经历Hopf分岔时,其兴奋性属于第二类型,而其PRC取值既有正又有负.在第三组参数条件下,当Iapp=39时ML模型的PRC既有正值又有负值,表现为第二类型的PRC.实际上,在第三组参数条件下,随着外加电流强度减小,ML模型经历一个次临界Hopf分岔产生阈上周期振荡,该周期振荡的极限环终止于一个鞍点同宿轨道分岔.对此情形尚无相关的文献给出周期振荡所对应的PRC类型.但由其分岔机理可知,周期振荡是由Hopf分岔引起的,因此其PRC表现为第二类型也是合乎情理的.同FHN神经元模型的PRC计算结果一样,ML模型的膜电位变化的尖峰时刻与其PRC取值的局部极值并不对应,这表明PRC仅取决于施加扰动的时间.对ML模型而言,其在不同参数条件下表现出不同的分岔行为,因此决定其PRC可以表现为第一类型或第二类型,从而可通过调节参数来实现PRC类型的改变.

4 方波扰动直接算法计算周期簇放电PRC

为了验证本文直接算法对周期簇放电PRC计算的有效性,我们选择HR神经元模型进行PRC计算,其主要原因是目前已有的文献中只有HR模型的PRC结果可资以参考.HR神经元模型形式如下［5]:

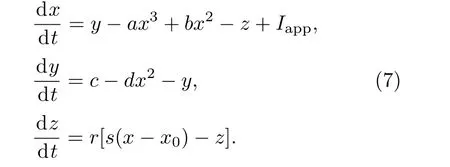
HR模型同FHN模型一样,是无量纲的.式中x表示神经元膜电位;y是峰变量,代表Na和K等快速离子通道电流;而z是簇变量,代表其他慢离子通道电流;a,b,c,d,s和x0为系统参数;r为快慢时间尺度因子;Iapp为外加电流强度.本文选取a=1.0,b=3.0,c=1.0,d=5.0,s=4.0,x=−1.6,r=0.001.

与前面周期峰放电情形不同的是,在计算周期簇放电PRC时,要注意所施加方波扰动的强度和持续的时间.本文中仅考虑弱扰动,其具体表现为不改变簇放电簇内的尖峰个数.如果尖峰个数在扰动下发生变化,则称该扰动为强扰动,如图9所示,实线是未扰动时簇放电模式,虚线是施加扰动后的簇放电模式,显然簇内尖峰个数发生了变化.当然在实际中强扰动亦有其意义,但本文中不讨论这一情形.值得注意的是,在算法实现过程中,参考相位一般选取第一个尖峰所对应的时刻.

当Iapp=1.3时,HR神经元模型簇内尖峰个数为5,其放电模式和对应的极限环如图10所示.

运用本文直接算法计算在该条件下HR神经元模型周期簇放电的PRC.其中Ip=0.05,tp=10,步长为0.0001,结果如图11所示.

图9 强扰动下周期簇放电簇内尖峰个数变化Fig.9.The variation of the number of spiking in a bursting under a strong perturbation.

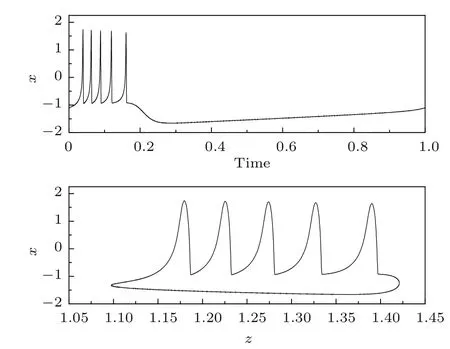
图10 HR神经元模型的周期簇放电模式及其对应的极限环Fig.10.Periodic bursting and its corresponding limit cycle in the HR neuron model.

运用无限小扰动的改进算法的计算结果如图12所示.

对比方波直接算法的结果与无限小扰动的改进算法的结果可知,二者仅存在PRC幅值大小的不同,而形状、波动趋势和正负性几乎完全相同.这表明本文方波扰动直接算法亦可适用于计算周期簇放电的PRC.同时通过HR神经元模型可以发现周期簇放电的PRC比周期峰放电的PRC有更为复杂的表现形式,最为明显的一点是周期簇放电的PRC存在一个剧烈变化的区域,正好对应于簇内放电部分.

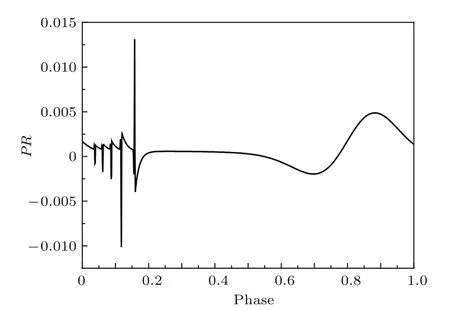
图11 方波扰动直接算法计算HR神经元模型周期簇放电的PRCFig.11.PRC of periodic bursting in the HR neuron model using the direct method with square wave perturbation.

图12 利用无限小扰动的改进算法时HR模型的PRCFig.12.PRC of periodic bursting in the HR neuron model using the modi fi ed direct method with in fi nitesimal perturbation.

5 结 论

本文提出了一个基于PRC的定义的方波扰动直接算法,通过HH神经元模型验证了该算法在计算周期峰放电的PRC是有效的.将该算法运用于FHN神经元模型,揭示了其PRC属于第二类型,这与FHN神经元模型随外加电流强度变化从静息态到周期峰放电所跨越的Hopf分岔动力学机理完全符合.然后考察了在三组不同的参数集条件下ML模型随外加电流强度变化的分岔行为,并计算了在各自周期峰放电或阈上周期振荡情形的PRC,表明通过调节相应的参数可改变神经元兴奋性类型,从而改变其PRC的类型,揭示了分岔机理与PRC类型之间的对应关系.最后通过HR神经元模型验证了本文算法对于计算周期簇放电的PRC也是可行的.通过大量的计算表明该算法对不同类型的簇放电具有通用性.我们已经计算了多种周期簇放电的PRC,至于周期簇放电神经元的PRC与周期簇放电的分岔机理之间的关系将在今后的工作进一步展开.本文的方波扰动直接算法计算速度介于无限小扰动的改进算法和典型峰扰动算法之间;在数值积分时积分步长对计算结果有明显的影响,当积分步长较大时,PRC不准确;当积分步长较小时,则会增加计算时间.方波扰动直接算法是从PRC定义出发设计的算法,计算过程中只需要确定方波扰动幅值Ip和持续时间tp.而典型峰扰动直接算法在计算时需要人为确定5个参数取值,并且方程还需增加一维.其他算法不是涉及伴随方程求解就是特征方程求解,这一关键步骤在计算分岔机理比较复杂的周期簇放电的PRC时往往会求解失败.这正是我们提出方波扰动直接算法的原因.

[1]Hodgkin A L,Huxley A F 1952J.Physiol.117 500

[2]FitzHugh R 1961Biophys.J.1 445

[3]Nagumo J,Arimoto S,Yoshizawa S 1962Proc.IRE50 2061

[4]Morris C,Lecar H 1981Biophys.J.35 193

[5]Hindmarsh J L,Rose R M 1984Proc.R.Soc.London Ser.B221 87

[6]Xu L F,Li C D,Chen L 2016Acta Phys.Sin.65 240701(in Chinese)[徐泠风,李传东,陈玲 2016物理学报 65 240701]

[7]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 221

[8]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 349

[9]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 583

[10]Fan Y S,Holden A V 1993Chaos Soliton.Fract.3 439

[11]Izhikevich E M 2000Int.J.Bifurcat.Chaos10 1171

[12]Gong P L,Xu J X 2001Phys.Rev.E63 031906

[13]Ding X L,Li Y Y 2016Acta Phys.Sin.65 210502(in Chinese)[丁学利,李玉叶 2016物理学报 65 210502]

[14]Gu H G,Zhu Z,Jia B 2011Acta Phys.Sin.60 100505(in Chinese)[古华光,朱洲,贾冰 2011物理学报 60 100505]

[15]Jin Q T,Wang J,Wei X L,Deng B,Che Y Q 2011Acta Phys.Sin.60 098701(in Chinese)[金淇涛,王江,魏熙乐,邓斌,车艳秋2011物理学报60 098701]

[16]Wang H X,Wang Q Y,Lu Q S 2011Chaos Soliton.Fract.44 667

[17]Yang Z Q,Guan T T,Gan C B,Zhang J Y 2011Acta Phys.Sin.60 110202(in Chinese)[杨卓琴,管亭亭,甘春标,张矫瑛2011物理学报60 110202]

[18]Longtin A 1993J.Stat.Phys.70 309

[19]Braun H A,Wissing H,Schäfer K,Hirsch M C 1994Nature367 270

[20]Wiesenfeld K,Moss F 1995Nature373 33

[21]Yu Y,Wang W,Wang J,Liu F 2001Phys.Rev.E63 021907

[22]Liu F,Wang J,Wang W 1999Phys.Rev.E59 3453

[23]Ermentrout B 1996Neural Comput.8 979

[24]Gutkin B S,Ermentrout G B,Reyes A D 2005J.Neurophysiol.94 1623

[25]Hastings J W,Sweeney B M 1958Biol.Bull.115 440

[26]Johnson C H 1999Chronobiol.Int.16 711

[27]Ikeda N 1982Biol.Cybern.43 157

[28]Tsalikakis D G,Zhang H G,Fotiadis D I,Kremmydas G P,Michalis L K 2007Comput.Biol.Med.37 8

[29]Ermentrout G B,Kopell N 1991J.Math.Biol.29 195

[30]Ermentrout G B 1992SIAM J.Appl.Math.52 1665

[31]Stiger T,Danzl P,Moehlis J,Neto ffT I 2010J.Med.Devices4 027533

[32]Shi X,Zhang J D 2016Chin.Phys.B25 060502

[33]Schultheiss N W,Prinz A A,Butera R J 2012Phase Response Curves in Neuroscience(New York:Springer)p3

[34]Ermentrout G B 2002Simulating,Analyzing,and Animating Dynamical Systems:a Guide to XPPAUT for Researchers and Students(Philadelphia:SIAM)p226

[35]Govaerts W,Sautois B 2006Neural Comput.18 817

[36]Sherwood W E,Guckenheimer J 2010SIAM J.Appl.Dyn.Syst.9 659

[37]Novicenko V,Pyragas K 2011Nonlinear Dynam.67 517

[38]Ermentrout G B,Terman D H 2010Mathematical Foundations of Neuroscience(New York:Springer)p51

PACS:05.45.–a,87.19.ll,87.19.lnDOI:10.7498/aps.66.090501

A direct algorithm with square wave perturbation for calculating phase response curve∗

Xie Yong†Cheng Jian-Hui

(State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,
Xi’an 710049,China)

25 November 2016;revised manuscript

6 January 2017)

Neuron is a typical dynamic system,therefore,it is quite natural to study the fi ring behaviors of neurons by using the dynamical system theory.Two kinds of fi ring patterns,i.e.,the periodic spiking and the periodic bursting,are the limit cycle oscillators from the point of view of nonlinear dynamics.The simplest way to describe the limit cycle is to use the phase of the oscillator.A complex state space model can be mapped into a one-dimensional phase model by phase transformation,which is helpful for obtaining the analytical solution of the oscillator system.The response characteristics of the oscillator system in the motion state of the limit cycle to the external stimuli can be characterized by the phase response curve.A phase response curve illustrates the transient change in the cycle period of an oscillation induced by a perturbation as a function of the phase at which it is received.Now it is widely believed that the phase response curve provides a new way to study the behavior of the neuron.Existing studies have shown that the phase response curve of the periodic spiking can be divided into two types,which are closely related to the bifurcation mechanism of neurons from rest to repetitive fi ring.However,there are few studies on the relationship between the phase response curve and the bifurcation type of the periodic bursting.Clearly,the fi rst prerequisite to understand this relationship is to calculate the phase response curve of the periodic bursting.The existing algorithms for computing the phase response curve are often unsuccessful in the periodic bursting.In this paper,we present a method of calculating the phase response curve,namely the direct algorithm with square wave perturbation.The phase response curves of periodic spiking and periodic bursting can be obtained by making use of the direct algorithm,which is veri fi ed in the four neuron models of the Hodgkin-Huxley,FitzHugh-Nagumo,Morris-Lecar and Hindmarsh-Rose.This algorithm overcomes the limitations to other algorithms in the application.The calculation results show that the phase response curve of the periodic spiking is determined by the bifurcation type.We fi nd a suprathreshold periodic oscillation starting from a Hopf bifurcation and terminating at a saddle homoclinic orbit bifurcation as a function of the applied current strength in the Morris-Lecar model,and its phase response curve belongs to Type II.A large amount of calculation indicates that the relative size of the phase response and its positive or negative value depend only on the time of imposing perturbation,and the phase response curve of periodic bursting is more complicated than that of periodic spiking.

phase response curve,spiking,bursting,bifurcation

10.7498/aps.66.090501

∗国家自然科学基金(批准号:11272241,11672219)资助的课题.

†通信作者.E-mail:yxie@mail.xjtu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11272241,11672219).

†Corresponding author.E-mail:yxie@mail.xjtu.edu.cn