过冷水溶液中的空间光孤子∗
欧阳世根
1)(华南师范大学,广东省微纳光子功能材料与器件重点实验室,广州 510006)2)(华南师范大学,广州市特种光纤光子器件重点实验室,广州 510006)
过冷水溶液中的空间光孤子∗
欧阳世根1)2)†
1)(华南师范大学,广东省微纳光子功能材料与器件重点实验室,广州 510006)2)(华南师范大学,广州市特种光纤光子器件重点实验室,广州 510006)
(2016年11月28日收到;2017年1月9日收到修改稿)
建立了在过冷水溶液中传播的光束的非局域非线性模型.过冷水的热致折射率扰动在温度扰动较小的情况下随温度增大,但在温度扰动达到一定程度后随温度减小.在求出该模型的数值孤子解后,对孤子的性态进行了研究.研究表明,在光功率较小时,过冷水表现出自聚焦的特性,而在光功率较大时,在孤子的中心区域的过冷水表现出自散焦的特性,而在孤子的外围仍表现为自聚焦.在总功率较大的情况下,孤子间的相互作用也表现出这种部分自散焦,部分自聚焦的现象.
非线性薛定谔方程,过冷,自聚焦,自散焦
1 引 言
近些年来,人们对非局域空间孤子进行了许多有趣的研究.对于非线性光学材料而言,若空间某点上的非线性折射率不仅依赖于该点处的光场,而且依赖于该点附近的一个区域内的光场,则称该非线性是空间非局域的.这种空间非局域的依赖关系可以有多种起源,例如,光折变材料中的光折变效应[1],向列相液晶中棒状分子间的相互作用[2],材料中与热输运有关的热致非线性[3−5].对于卷积型的非局域非线性,如向列相液晶中的非线性[2]和铅玻璃中的热致非线性[3],在强非局域条件下,即非局域响应长度远大于光束束宽时,空间光孤子间的相互作用总是表现出相互吸引的特性.并且由于非局域的特点,光束间的相互作用的距离可以得到有效的增大.
本文研究的对象是热致非线性,其本质是空间非局域的.对于铅玻璃,其折射率随温度增大而线性地增大,因此铅玻璃表现出热致的自聚焦效应,可以支持空间亮孤子[3].而对于大多数的液体或气体,它们的折射率随温度增大而线性地减小,表现出热致的自散焦效应,可以支持空间暗孤子[4,5].上述两种自聚焦或自散焦的热致的非线性折射率均与温度差Δt成正比,只是符号不同而已,即Δn=β1Δt,其中β1> 0为自聚焦,β1<0为自散焦.本文研究高阶的非线性效应,即Δn=β1Δt+β2(Δt)2的情况.过冷水溶液的折射率就具有这样的形式[7−9].研究表明,对于这样的系统,随着入射光功率的增大,材料可以由自聚焦转变为局部自散焦,从而可以支持新的空间孤子形式,光束的相互作用既不像自聚焦也不像自散焦,而呈现出新的特点.
2 过冷水溶液中的光束演化方程
标准大气压下,纯水在t>0◦C温度下的稳定物态为液态,而在t<0◦C的稳定物态为固态.但在缺少结晶核的情况下,例如缓慢地使液态水从t> 0◦C降温到t< 0◦C,液态纯水可在t< 0◦C保持液态而不结冰.低于冰点而不结冰的液态水处在热力学中的亚稳态,称为过冷水.一旦往过冷水中引入结晶核,例如猛烈摇晃,过冷水会迅速结冰,转变为固态.一定条件下某些水溶液,例如可乐饮料、啤酒等,也存在过冷的现象.众所周知,液态水的质量密度存在着反常现象[6],在t=4◦C附近,液态水的密度达到最大值,比0◦C的水的密度大.此外,液态水的折射率也存在着反常现象.根据文献[7—9]的数据可粗略地估算出,对于波长为501和589 nm的光,液态水的折射率在−5◦C≤t≤5◦C温度范围内随温度的变化呈近似抛物线型的依赖关系
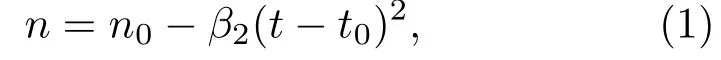
这里t0=−0.1◦C,β2=3×10−6K−2,对于波长为501和589 nm的光n0分别为1.337733或1.334334.由于β2>0,所以液态水的折射率在温度为t0时达到最大值n0;对于温度t<t0,液态水的折射率随温度的升高而增大;对于温度t>t0,折射率随温度升高而减小.电解质水溶液的折射率随温度的变化也可由(1)式近似地描述,只需对参量n0,β2,t0做相应的调整[10].
纯水对可见光的吸收是非常弱的[11],对于波长为460—660 nm的光,吸收率仅为α=0.01—0.41 m−1.但某些水溶液对特定波长的光有很强的吸收.例如,紫红色的KMnO4的水溶液对于500—560 nm附近的绿色光有很强的吸收,浓度为1.8×10−6mol/L的KMnO4溶液对528 nm的光的吸收率可达α=1 m−1;橙色的K2Cr2O7水溶液则对480—490 nm的光有较强吸收;蓝色的CuSO4水溶液对580—600 nm的光有较强的吸收.
考虑下面的实验设计.波长λ=514 nm的激光束E(X,Y,Z)=U(X,Y,Z)eikZ入射到放置在温度保持在t1的恒温箱(t1<t0)内的折射率为n1=n0−β2(t1−t0)2的KMnO4水溶液中,这里X,Y,Z为实验室坐标系,Z轴为光束的传播方向,k=n12π/λ,U为光束电场的慢变包络.在光束传播路径上,由于水溶液对光的吸收并把光能转化为水的热能,光束传播路径上的水溶液的温度由t1升高变为t(X,Y,Z).记温度扰动为T=2(t−t1)/(t0−t1),那么由(1)式可求得水溶液的折射率n=n1+Δn,其中
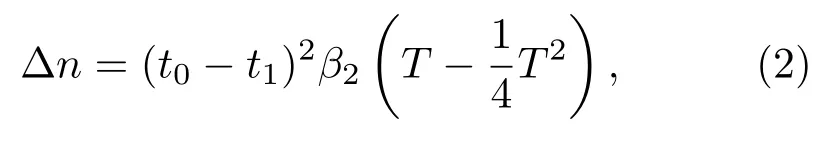
Δn为温度扰动T所引起的折射率扰动.容易看出,当T<2时,Δn随T的增大而增大;当T>2时,Δn随T的增大而减小.另一方面,若恒温箱的温度t1大于t0,那么由于光束入射后的温度升高,t>t1,因此由(1)式知,水溶液的折射率n随温度t增大而减小,这时水溶液具有自散焦效应,可以支持暗孤子,文献[4,5]对此有详细的论述,对此本文不做进一步描述.本文的其余部分均假定t1<t0,不再赘述.
从(2)式可以看出,要计算水溶液的折射率分布Δn(X,Y,Z)必须已知水溶液的温度分布T(X,Y,Z).稳态下,温度扰动T由如下泊松方程决定:

其中,I=ε0c|E|2为激光束的光强,c为光速;κ为水溶液的热导率,在本文感兴趣的范围内可认为κ =0.55 W.m−1.K−1,不依赖于温度和溶液的浓度[12].一旦确定空间折射率分布,忽略光吸收损耗(由下面的讨论可知该近似是合理的),那么由时谐亥姆霍兹方程

原则上就可以确定激光束的传播.在旁轴近似下,由时谐亥姆霍兹方程出发可获得激光束慢变包络的演化方程


3 孤子的性态
定义光束的功率和束宽分别为

那么在低功率极限(p≪ 1)下,由(5)式可知T≪1,从而T2≪T,这时方程(6)退化为

考虑半径为R的圆柱型容器,光孤子沿圆柱容器的旋转对称轴(即z轴)传播.设方程(9)的孤子解为

这里ψ(r)为孤子的轮廓,γ为孤子的传播系数.在大于束宽的区域(r≫ w),对于孤子有ψ(r)=0.由于处在恒温箱内,所以有边界条件T(R)=0.在大于束宽的区域(R≥r≫w),由高斯积分变换公式(矢量场在闭曲面上的通量等于矢量场的散度在闭曲面所包围区域中的体积分)[13]求解方程(5),可得

设功率为p,束宽为w的孤子u(r,z)=ψ(r)eiγz在容器中传播时引起的温度扰动分布为T(r),那么容易验证,束宽为原束宽w的µ倍,功率为原功率p的1/µ2的另一束光
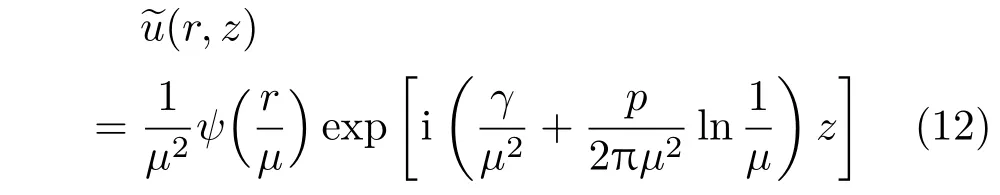
仍是孤子解;相应地,其引起的温度扰动分布为


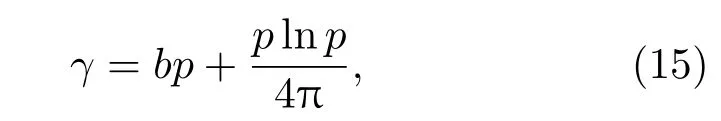

图1 R=50lc时,光功率p=1,3,5,7,9时的(a)温度分布T(r)、(b)折射率分布N(r)、(c)基态光孤子的包络ψ(r)Fig.1.(a)The light-induced temperature perturbations T(r),(b)the perturbed refractive index N(r),and(c)the fundamental solitons ψ(r)of light powers p=1,3,5,7,9 respectively,when R=50lc.
随着孤子功率p的增大,温度的扰动越来越大,T2/4变得可以与T相比较.这时,可以通过数值求解耦合方程(5)和(6)获得孤子解.图1所示为不同功率(p=1,3,5,7,9)下的孤子解ψ(r)和相应的温度扰动T(r)以及折射率扰动N(r).在功率p足够大(例如p=9)时,由于系统处在恒温器中,内部液体吸收光能而变热,所以温度T总是从外围往内部单调地增大,即随r减小而单调增大,在某个半径范围内,温度扰动T>2;由此,折射率扰动N=T−T2/4=1−(1−T/2)2从最外围N(R)=0随半径r减小而连续增大,并在某个半径达到最大值N=1后随r减小而变小,于是外围区域的折射率分布表现为聚焦,而中心区域表现为散焦.由于上述原因,功率足够大(例如p=9)的孤子的光强在内部会出现凹陷.图2给出了功率p=8的孤子在横向截面处的光强分布,以及对其沿z轴传播的数值模拟结果.
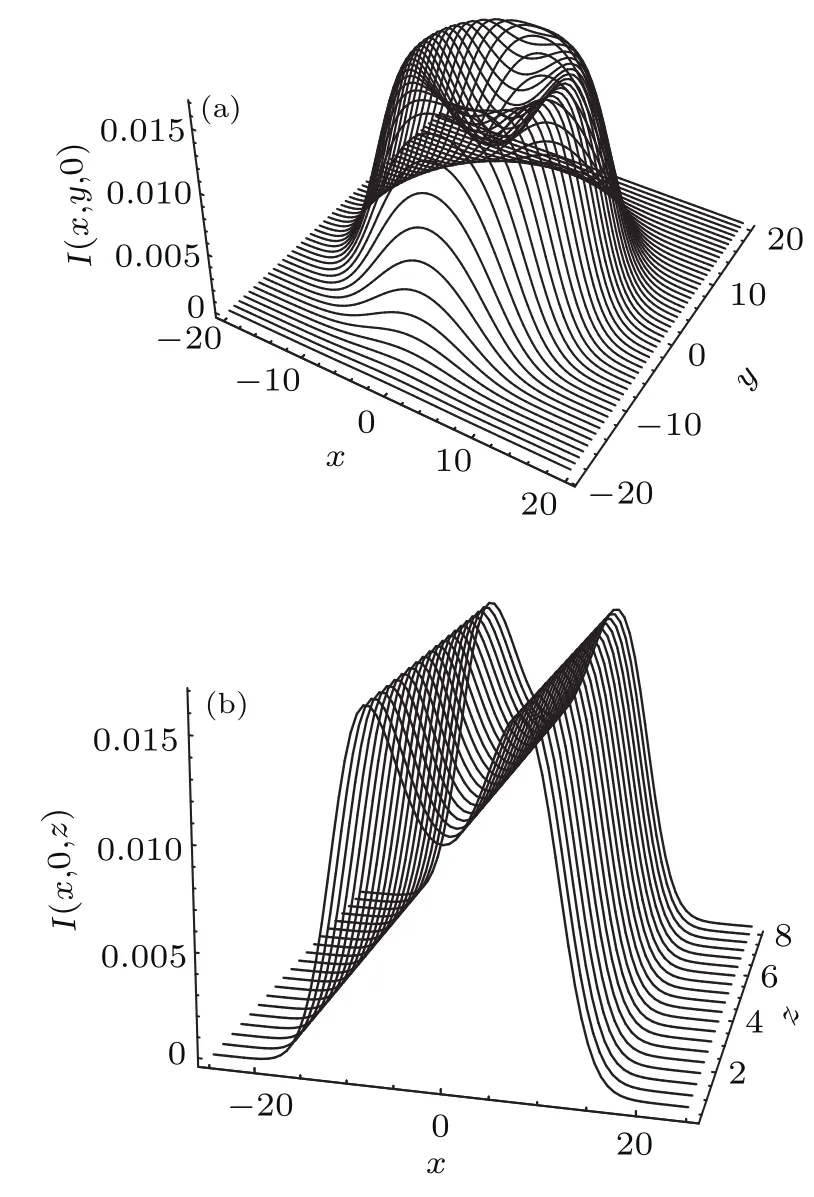
图2 功率p=8时,(a)孤子解在横向的光强分布;(b)孤子沿z轴传播的数值模拟结果Fig.2.(a)The soliton’s light intensity distribution I(x,y,0)at input face z=0 and(b)its propagation along z axis.Here the soliton’s light power is p=8.
通过数值求解,我们还求出了孤子的束宽w和传播常数γ是如何随孤子功率p而变化的,如图3所示.可以看出,(14)和(15)式可以准确地描述低功率(p<1)孤子的束宽w和传播常数γ对功率的依赖关系,但随着p增大到一定程度时,(14)和(15)式明显偏离了实际情况.特别地,(15)式预言传播常数γ单调地随功率p而增大,其增大是没有限制的,而真实的情况是,对于甚大功率p的孤子,其传播常数趋向饱和,即γ→ 1.对于后者,这里尝试给出一个定性的理解.把纵向变量z理解为时间t,那么非线性薛定谔方程(6)中的折射率的相反数(−N)=−1+(1−T/2)2相当于势阱,而传播常数的相反数(−γ)相当于本征态ψ的本征能量. 在忽略动能项后−γ≈〈ψ|(−N)|ψ〉/〈ψ|ψ〉,由此,考虑到N ≤1,所以有γ≤1.从传输光学的角度也可以对此做定性的理解.由于在介质中单色光波矢的大小与介质的折射率成正比,所以非线性折射率引起的波矢的增量为kΔn/n1,经传输距离后非线性相位的增量为其中利用了特征长度lc的定义以及(2)式.由于T−T2/4=1−(1−T/2)2≤1,所以非线性相位的增量(T−T2/4)z≤z.由孤子解(10)式的定义,孤子的非线性相位增量为γz,这就表明γ≤1.可见,γ的饱和性反映非线性折射率的饱和性.对于束宽,(14)式在大功率p处存在明显的偏离,前者预言束宽随功率单调减小,而实际情况是束宽在随功率减小到某个最小值后随功率增大.对此,这里也尝试给出一个定性的理解.由(11)式或图1(a)均可看出,对于不同的功率,达到相同温度T(T<2)的半径r是不同的,功率p越大,半径r越大.由于T<2的区域是聚焦区域,而T>2的区域为散焦区域,因此,随着p的增大,聚焦区域往外移,这样光就被聚焦在外移的聚焦区,导致对于甚大功率的孤子的束宽随功率增大.
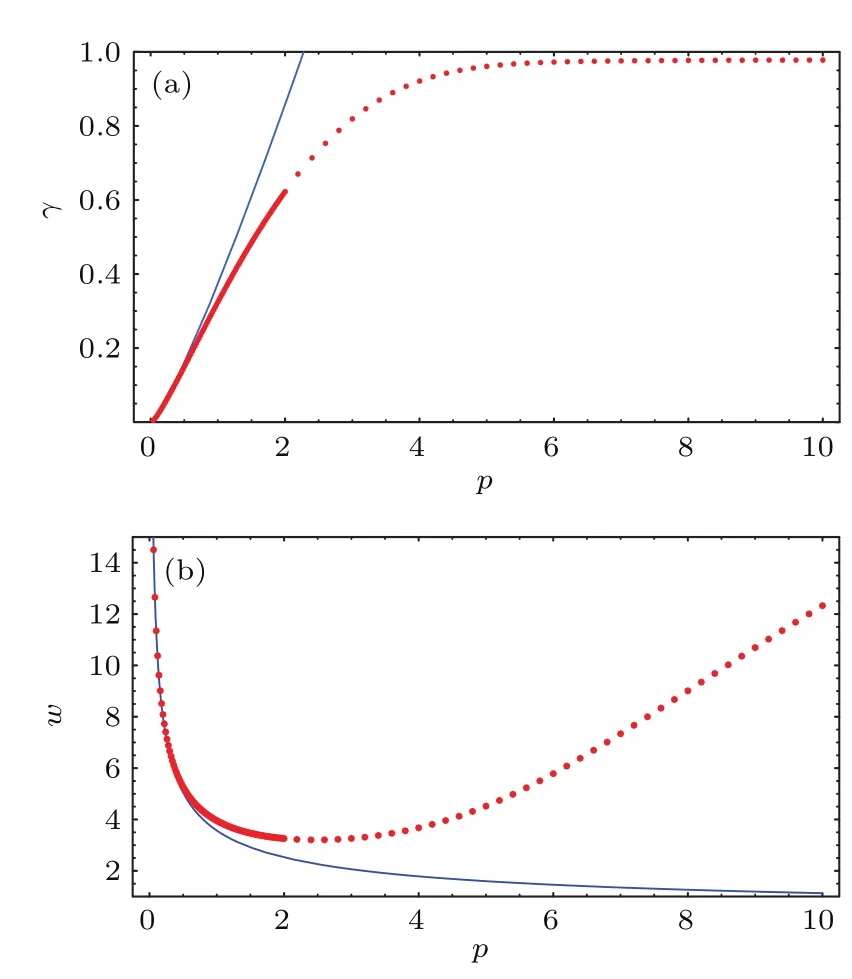
图3 (网刊彩色)(a)传播常数γ随功率p的变化,其中红点为孤子解,蓝线为依据(15)式获得;(b)束宽w随功率p的变化,其中红点为孤子解,蓝线为依据(14)式获得Fig.3.(color online)(a)Dependence of the propagation constant γ on the light power p,where red dots represent soliton solutions and the blue line is depicted according to Eq.(15);(b)dependence of the beam width w on the light power p,where red dots represent soliton solutions and the blue line is depicted according to Eq.(14).
4 孤子的相互作用
已有大量的研究表明,在对入射光具有热致非局域响应的铅玻璃中两束光的相互作用总是表现为相互吸引.这里,我们利用模型(5)和(6)对在过冷水中两束光的相互作用进行数值模拟研究.过冷水的非线性也是起源于对入射光的热致非局域响应,但与铅玻璃不同,后者的折射率扰动正比于温度的扰动,而前者的折射率扰动先随温度增大而增大,后随温度增大而减小.这对光束的相互作用产生了重大的影响.图4给出了入射功率均为p=5,束宽均为w=6.6的两束高斯光束在中心距离d=14的情况下同时入射到过冷水中,它们的相互作用在不同传播距离z下的图样.由图4可以看出,由于横截面坐标原点附近的温度最大,并且T>2,所以坐标原点附近区域为散焦区,而两光束的外侧为低温区,为聚焦区域,因此光能被吸引到(或被排斥到)外围的一个环带中,并且该环带的尺寸还随着传播而扩大.

图4 入射束宽均为6.6,中心距离为14的两束功率均为p=5的光束的相互作用图样Fig.4.Interaction patterns at di ff erent propagation distance z of two Gaussian beams initially separated by a distance of d=14,where the two Gaussian beam’s widthes are w=6.6 and their power is p=5.
5 总 结
本文建立了在过冷水溶液中传播的光束的非局域非线性模型.过冷水的热致折射率扰动在温度扰动较小的情况下随温度增大,但在温度扰动达到一定程度后随温度减小.在求出该模型的数值孤子解后,对孤子的性态进行了研究.研究表明,功率甚大的孤子的传播常数趋于饱和,而其束宽趋于随功率增大.这与过冷水在甚大功率光入射时高温区域表现为自散焦,而低温区域表现为自聚焦的特性有着直接的联系.过冷水的这种特性还强烈地影响着在其中传播的大功率光束之间的相互作用过程.
我院此次研究通过对比两组不同的护理服务措施,探讨分析了良肢位摆放在脑卒中偏瘫患者的治疗效果、患者的护理服务满意度和生活质量。通过对比常规护理服务措施和在执行常规护理服务措施的同时,额外在患者入院时采取良肢摆放的方法,发现采用增加采取良肢摆放的方法,不仅可以提高患者的治疗效果,改善患者的生活质量,而且可以增加患者的护理服务满意度。
参考文献
[1]She W L,Lee K K,Lee W K 1999Phys.Rev.Lett.83 3182
[2]Assanto G,Fratalocchi A,Peccianti M 2007Optics Express15 5248
[3]Rotschild C,Cohen O,Manela O,Segev M,Carmon T 2005Phys.Rev.Lett.95 213904
[4]Zhou L H,Gao X H,Yang Z J,Lu D Q,Guo Q,Cao W W,Hu W 2011Acta Phys.Sin.60 044208(in Chinese)[周罗红,高星辉,杨振军,陆大全,郭旗,曹伟文,胡巍 2011物理学报60 044208]
[5]Wang J,Zheng Y Z,Zhou L H,Yang Z J,Lu D Q,Guo Q,Hu W 2012Acta Phys.Sin.61 084210(in Chinese)[王婧,郑一红,周罗红,杨振军,陆大全,郭旗,胡巍2012物理学报61 084210]
[6]Vedamuthu M,Singh S,Robinson G W 1994J.Phys.Chem.98 2222
[7]Luten D B 1934Physical Review45 161
[8]Robinson G W,Cho C H,Gellene G I 2000J.Phys.Chem.B104 7179
[9]Cho C H,Urquidi J,Gellene G I,Robinson G W 2001J.Chem.Phys.114 3157
[10]Colcombe S M,Lowe R D,Snook R D 1997Analytica Chimca Acta356 277
[11]Pope R M,Fry E S 1997Applied Optics36 8710
[12]Benchikh O,Fournier D,Boccara A C,Teixeira J 1985J.Physique46 727
[13]Zhao K H,Chen X M 1997Electromagnetics(2nd Ed.)(Beijing:Pubishing House of Higher Education)pp45–69(in Chinese)[赵凯华,陈熙谋 1997电磁学 (第二版)(北京:高等教育出版社)第45—69页]
PACS:05.45.Yv,42.65.TgDOI:10.7498/aps.66.090505
Optical spatial solitons in supercooled aqueous solutions∗
Ouyang Shi-Gen1)2)†
1)(Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices,South China Normal University,Guangzhou 510006,China)2)(Guangzhou Key Laboratory for Special Fiber Photonic Devices,South China Normal University,Guangzhou 510006,China)
28 November 2016;revised manuscript
9 January 2017)
In recent years,nonlocal spatial solitons have attracted a great deal of attention.Optical spatial solitons result from the suppression of beam di ff raction by the light-induced perturbed refractive index.For spatial nonlocal solitons,the light-induced perturbed refractive index of medium depends on the light intensity nonlocally,namely,the perturbed refractive index at a point is determined not only by the light intensity at that point but also by the light intensity in its vicinity.Such a spatial nonlocality may originate from heat transfer,like the nonlocal bright solitons in lead glass and dark solitons in liquids or gases.The perturbed refractive index Δn of lead glass or liquid is direct proportional to the light-induced temperature perturbation Δt,i.e. Δn=β1Δt.The proportional coefficient β1is positive(negative)for lead glass(liquid),and the light-induced temperature perturbation Δt is determined by the Poisson equation∇2(Δt)=−DI,where I is the light intensity and D is a coefficient.In this paper,we investigate another type of thermal nonlinear e ff ect,in which the perturbed refractive index Δn depends on the light-induced temperature perturbation Δt in a new way that Δn=β1Δt+ β2(Δt)2.It has been indicated previously that the refractive index of a supercooled aqueous solution depends on the temperature,speci fi cally n(t)=n0−β2(t−t0)2,where n0=1.337733 for 501 nm light wave,t0=−0.1◦C and β2=3×10−6K−2.So for t< t0,the refractive index of aqueous solution increases with temperature rising,while t>t0,it decreases with temperature increasing.In this paper,we use the numerical simulation method to investigate the propagation and interaction properties of optical solitons propagating in a supercooled aqueous solution,whose temperature on boundary is maintained at some value below t0,with the aqueous solution placed in a thermostatic chamber.Obviously,the inner temperature of the solution rises,owing to absorbing some optical energies of the light beam propagating in it,and as a consequence the inner refractive index changes according to n(t)=n0−β2(t− t0)2.For a soliton with a low power,the inner temperature t of the solution is always kept below t0,so the refractive index at a point with a higher t is larger than that at another point with a lower t.In this case,the solution behaves as a self-focusing medium.A soliton with a higher power has a narrower beam width and a larger propagation constant,and the soliton takes a bell shape.However,for a soliton with a rather high power,the temperature in the core will be higher than t0while the temperature in the periphery is still below t0.Therefore,the part of the solution in the core behaves as a self-defocusing medium while the part in the periphery behaves as a self-focusing medium.For such a case,the higher the power of the soliton,the larger the radius of the core is and the larger the beam width of the soliton,so the soliton takes a crater shape with a saturated propagation constant.Finally we also investigate the interaction between two solitons in a supercooled aqueous solution.For two neighboring beams with a rather high total power,they cannot maintain their individualities any more during the interaction,but merge into an expanding crater.
Schrödinger equation,supercooled,self-focusing,self-defocusing
10.7498/aps.66.090505
∗国家自然科学基金(批准号:61008007)资助的课题.
†通信作者.E-mail:ouyang.shigen@163.com
*Project supported by the National Natural Science Foundation of China(Grant No.61008007).
†Corresponding author.E-mail:ouyang.shigen@163.com

