六面顶压机立方压腔内压强的定量测量及受力分析∗

王海阔 任瑛 贺端威 许超

1)(河南工业大学材料科学与工程学院,材料压处理研究所,郑州 450001)2)(四川大学原子与分子物理研究所,高压科学与技术实验室,成都 610065)3)(武汉科技大学理学院,武汉 430065)

六面顶压机立方压腔内压强的定量测量及受力分析∗

王海阔1)†任瑛1)贺端威2)许超3)

1)(河南工业大学材料科学与工程学院,材料压处理研究所,郑州 450001)2)(四川大学原子与分子物理研究所,高压科学与技术实验室,成都 610065)3)(武汉科技大学理学院,武汉 430065)

(2016年12月31日收到;2017年2月4日收到修改稿)

将六面顶压机立方压腔内置入电路,采用原位电阻测量确定Bi,Tl,Ba相变的方法,标定了压腔内不同位置的压力(强).通过标定立方压腔顶锤表面的压力并结合计算,分别得到了外部加载与压腔密封边受力以及合成腔体受力的对应关系.实验分析结果表明,随着外部加载的增加,当腔体压力达到5 GPa时,消耗在压腔密封边上的加载急剧上升,消耗在合成腔体的加载趋于不变,从而导致立方压腔压力达到上限.利用实验结果,分析了立方压腔在高压下的受力状态,解释了立方压腔的压力难以超过7 GPa的原因.结合立方压腔的几何结构,通过理论分析,提出了采用高体弹模量的物质作为传压介质,同时采用低体弹模量的物质作为密封边提高立方压腔压力上限的可行方案.通过定量标定叶腊石压腔轴向的压力梯度,给出了压腔内沿对称轴不同位置压力值的计算方法,此方法可为高压实验提供更精确的压力数据.

高压技术,立方压腔,压腔受力分析,压强定量测量

1 引 言

压力(强)类同于温度与化学组分,是决定物质存在状态与导致结构物性改变的基本热力学要素之一.高压科学与技术可广泛应用于物理学、材料学、化学、地学与行星科学等领域［1−9].高压实验技术是进行高压下材料合成及物性研究的物质基础.

高压实验技术分为静高压技术与动高压技术,其中静高压实验技术又分为大腔体(样品尺寸大于1 mm3)静高压技术与小腔体静高压技术(如:金刚石对顶砧).金刚石对顶砧可产生高于600 GPa的压力［10],并可与同步辐射光源等实验手段结合,对物质在极高压力条件下的结构和物性行为进行原位观测［8,11−14],但金刚石对顶砧装置的样品腔直径一般只有几个到几百微米.大腔体静高压装置一般可分为一级大腔体静高压装置与二级(或多级)大腔体静高压装置.应用最广的二级(或多级)大腔体静高压装置通常又称八面体压机,由八个二级顶锤和八面体传压介质组成的二级(末级)增压单元置于一级(前级)压腔内产生高压,若采用硬质合金二级顶锤,可产生的最高压强约为25 GPa［15],若采用多晶金刚石二级顶锤,压强极限可提高至80 GPa以上［16,17].一级大腔体静高压装置主要包括两面顶与多面顶压腔装置［18−20].两面顶压腔装置如:凹曲面压腔、年轮式压腔、柱塞式压腔所能产生的最高压强分别约为15,8,5 GPa［12−26],其中凹曲面压腔与柱塞式压腔多用于科学研究,年轮式压腔主要用于工业生产.一级多面顶压腔装置主要包括四面顶压机与六面顶压机.其中,四面顶压机已很少用于科研与生产;六面顶压机因具有操作方便、自对中性好、实验成本低等优点而被广泛应用于科研与生产领域,当六面顶压机顶锤作用面的面积大于20 mm× 20 mm时,其可产生的压强一般不超过7 GPa［27,28],采用叶腊石与氧化镁混合组装及顶锤-预密封边加压系统可将六面顶压腔的最高压力提升至约9 GPa［24,26].

在六面顶立方压腔产生高压的过程中,传压介质经历了塑性变形(密封边形成前)及弹性形变(密封边形成后)的过程.理论模拟表明,六面顶压机压腔的力学结构是限制其产生更高压力的主要制约因素［28],在不同外部加载下,实验测量六面顶压机压腔密封边及合成腔体的受力情况,对设计可产生更高压力的新型立方压腔具有指导意义,而采用常规的压力标定方法测量六面顶压机立方压腔密封边及合成腔体的受力情况比较困难.另外,六面顶压机多采用固体叶腊石作为传压介质,固体传压介质内的压力场分布导致同一外部加载下压腔内不同位置的压力不同,为了获得精确的实验数据,需对六面顶压机压腔内不同位置的压力进行精确测量.

本文将六面顶压机立方压腔内置入电路,通过标定压腔顶锤表面压力并结合计算,得到了六面顶立方压腔密封边、合成腔体的受力与外部加载的关系.利用这一实验结果,解释了六面顶压机常规压腔的压力难以超过7 GPa的原因,并给出了提高六面顶立方压腔压力的可行方案.另外,本文通过定量标定叶腊石立方压腔轴向的压力梯度,给出了立方压腔内沿对称轴不同位置压力值的计算方法,此方法可为高压实验提供更精确的压力标定数据.

2 压力标定实验的设计

2.1顶锤表面压力及压腔轴向压力梯度标定实验设计

图1所示为六面顶压机的压腔系统.实验采用模压叶腊石(密度:2.65 g/cm3,北京门头沟)为传压介质,加压前在300◦C的温度下烘烤12 h.立方体传压介质的边长为32.5 mm,硬质合金顶锤作用面的边长为23.5 mm.为了测量顶锤表面(叶腊石压腔表面)的压力及定量测量传压介质内的压力梯度,叶蜡石立方体被加工成三部分,如图2所示.细丝状(直径约0.01 mm,铜箔间的距离约0.1 mm)的标压物质Bi,Tl和Ba被放置在沿着立方体传压介质对称轴的片状传压介质表面中心(压标物质在不同位置受剪程度不同,剪应力对相变有影响,大压机压腔内的剪切力不大,忽略剪应力对相变压力的影响是大压机标压的常规做法).我们使用铜箔(厚度0.01 mm)作为导线与硬质合金顶锤相连(硬质合金顶锤与压机框架绝缘),电路连接如图2所示.固定电路后,三片传压介质组装成一个立方体(32.5 mm× 32.5 mm× 32.5 mm)放入六面顶压机压腔内.图2所示电路可同时监测压腔内不同位置的Bi,Tl或Ba的电阻变化,并由多通道记录仪的不同通道记录.当同一压腔内不同位置的Bi,Tl或Ba发生相变(电阻发生突变),对应的表压(外部加载力)同时也被多通道记录仪记录,这样,立方腔体表面及沿立方体压腔对称轴不同位置的压力与外部加载的关系就被确立.加压结束后使用千分尺测量标压物质两点间的距离,再算出相同外部加载下沿立方体传压介质对称轴不同位置的压力差,我们就可以得到叶腊石传压介质轴向的压力梯度,进而计算轴向各点的压力.

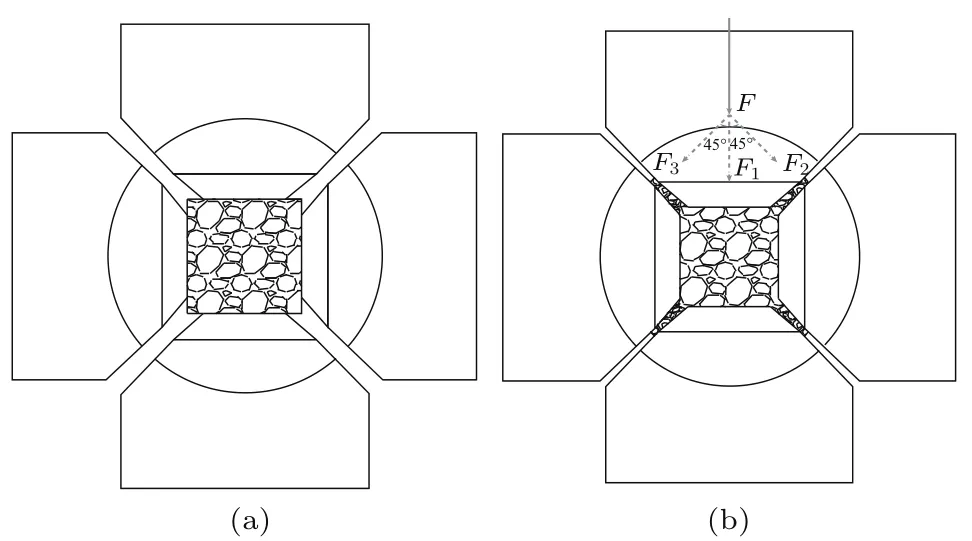
图1 六面顶压机压腔系统的剖面示意图 (a)为加压开始时;(b)为加压结束时Fig.1.High-pressure cell in large volume cubic press:Pressure media(a)at the beginning and(b)at the end of the pressurizing stroke.

图2 (网刊彩色)测量压腔表面压力及沿立方体传压介质对称轴的压力梯度的标压电路组装示意图Fig.2.(color online)Schematic illustration of the cell assembly used for measuring pressure at the face of the cubic cell and pressure gradient along the axis of symmetry of the cell.

2.2顶锤表面压力分布均匀性及压腔轴向压力梯度分布均匀性的测量实验设计

为了估算顶锤表面压力分布的不均匀性所引起的测量误差,我们把两个切成细丝状的铊放在叶腊石表面中心及与之相距8 mm的位置,以便测量高压下立方体叶腊石表面不同位置的压强是否相同(图3).

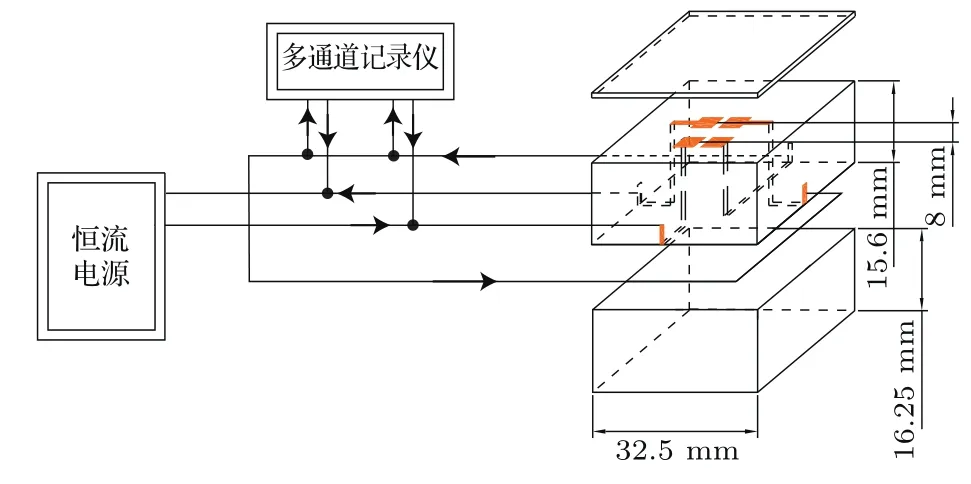
图3 (网刊彩色)测量立方体传压介质表面压力均匀性的标压电路组装示意图Fig.3.(color online)Schematic illustration of the cell assembly used for measuring the distribution of the pressure at the face of the cubic cell.

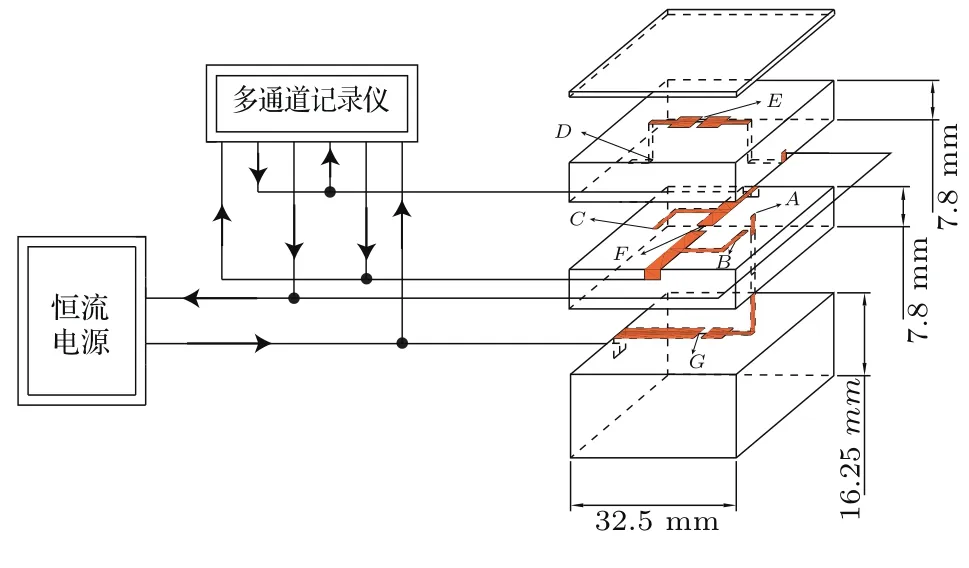
图4 (网刊彩色)测量沿立方体传压介质对称轴压力梯度均匀性的标压电路组装示意图Fig.4.(color online)Schematic illustration of the cell assembly used for measuring the distribution of the pressure gradient along the axis of symmetry of the cubic cell.

为了估算沿立方体传压介质对称轴压力梯度的不均匀性所引起的误差,我们把三个切成细丝状的铊放在沿立方体传压介质对称轴的三个不同位置,以便测量在相同加载下沿传压介质对称轴不同区域压力梯度的差别.如图4所示,标压物质铊分别置于E点(传压介质表面中心),G点(传压介质体中心)和F点(传压介质表面中心和体中心连线中点).4个叶腊石片可组装成一个传压介质立方体,组合后A点和B点连接,C点和D点连接,从而使得整个电路成为通路.压力标定过程中,我们可以同时监测E点、G点和F点的标压物质的电阻变化,从而建立传压介质压腔内三个不同点的压力与外部加载的关系.

3 压力标定实验结果

3.1顶锤表面压力及立方压腔体中心压力标定结果

实验采用金属Bi在2.55 GPa、Tl在3.67 GPa、Ba在5.5 GPa的高压相变(电阻突变)［29]对沿叶腊石立方传压介质对称轴的表面中心和体中心压力进行标定.图5、图6和图7分别为我们获得的沿叶腊石立方体传压介质对称轴的表面中心和体中心Bi,Tl,Ba的典型电阻与外部加载的关系.

图5 (网刊彩色)沿传压介质对称轴的表面中心和体中心Bi的电阻与外部加载的关系Fig.5.(color online)The resistances of two Bi wires at various positions versus the press load along the axis of symmetry of the cubic cell.

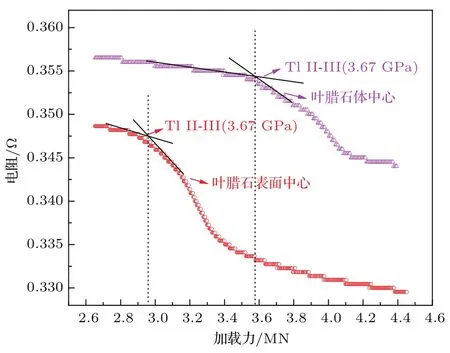
图6 (网刊彩色)沿传压介质对称轴的表面中心和体中心Tl的电阻与外部加载的关系Fig.6.(color online)The resistances of two Tl wires at various positions versus the press load along the axis of symmetry of the cubic cell.

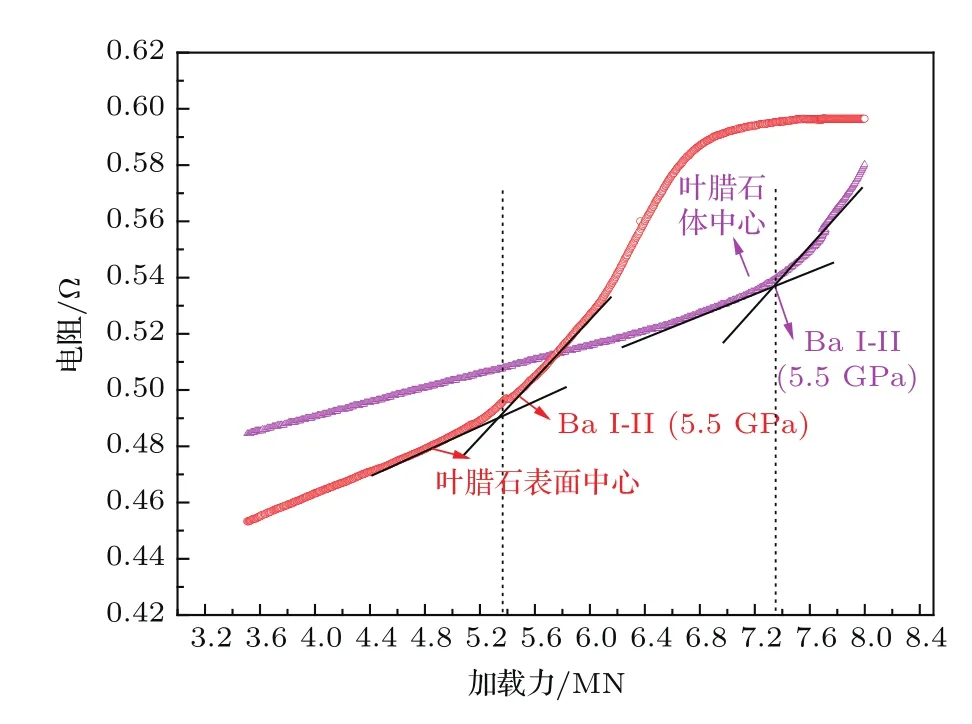
图7 (网刊彩色)沿传压介质对称轴的表面中心和体中心Ba的电阻变化与外部加载的关系Fig.7.(color online)The resistances of two Ba wires at various positions versus the press load along the axis of symmetry of the cubic cell.

表1列出了标压物质Bi,Tl,Ba沿着叶腊石立方体传压介质对称轴的表面中心和体中心的相变压力与外部加载的对应值.由表1可知,对于同一标压物质的相变点,置于表面中心的标压物质要早于置于体心的标压物质发生相变;随着腔体压力的增加,压腔内不同点相同标压物质发生相变的油压差也在增大,这表明压腔内的压力梯度随着腔体压力的增加而增大.

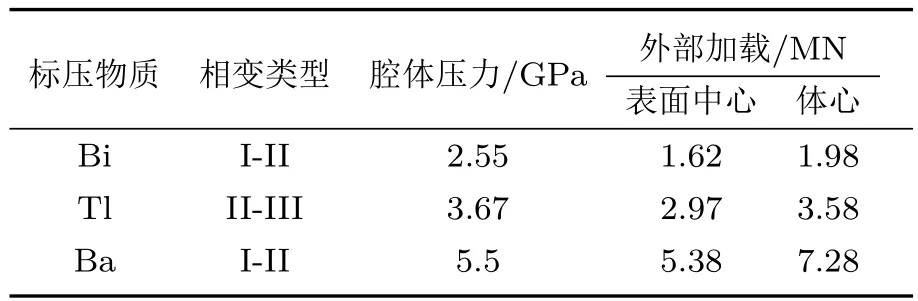
表1 标压物质Bi,Tl,Ba在传压介质表面中心和体心的相变压力与外部加载的对应值Table 1. Pressure calibration for the pyrophyllite pressure-transmitting medium at various positions.

3.2顶锤表面压力分布均匀性及压腔轴向压力梯度分布均匀性测量结果

图8所示为叶腊石立方体传压介质表面(忽略压腔表面叶腊石薄片的厚度)不同位置Tl的电阻与外部加载的关系.由图8可知,位于叶腊石立方体传压介质表面中心的Tl丝及与之相距8 mm(由于叶腊石的流动,卸压后两个Tl丝相距8.5 mm)的Tl丝发生相变时所对应的外部加载均为2.97 MN,表明在相同外部加载下,六面顶压腔系统顶锤表面不同位置的压力基本一致.

图9所示为沿叶腊石立方体传压介质对称轴不同位置Tl的电阻与外部加载的关系.由图9可知,位于叶腊石立方体传压介质表面中心(E点)与体心(G点)连线中点(F点)的Tl的相变(3.67 GPa II–III)发生时所对应的外部加载为3.25 MN,在这个加载下,E点和G点所对应的压力分别为3.94和3.43 GPa(见图11).由此我们可以得到E点和F点之间的平均压力梯度约为39.7 MPa/mm≈ [(3.94−3.67)×1000 MPa/6.8 mm],F点和G点之间的平均压力梯度约为35.3 MPa/mm≈[(3.67−3.43)×1000 MPa/6.8 mm].如图12所示,本文给出的叶腊石立方体沿对称轴的平均压力梯度是37.5 MPa/mm≈ [(3.94−3.43)×1000 MPa/13.6 mm].由以上分析可知,沿叶腊石传压介质立方体对称轴压力梯度的不均匀性所引起的实验误差约为6%.

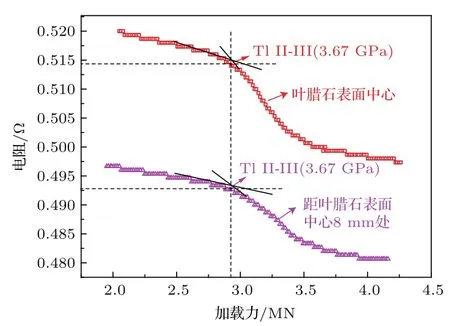
图8 (网刊彩色)传压介质表面不同位置Tl的电阻与外部加载的关系Fig.8.(color online)The resistances of two Tl wires at various positions versus the press load at the face of the cubic cell.

图9 (网刊彩色)传压介质对称轴不同位置Tl的电阻与外部加载的关系Fig.9.(color online)The resistances of three Tl wires at various positions versus the press load along the axis of symmetry of the cubic cell.

3.3加压后叶腊石表面中心与体心两点之间距离的测量

在7.3 MN的外部加载下,叶腊石体中心的压力约为5.5 GPa,卸压后立方体传压介质的边长为27.9 mm(实验均在低于7.3 MN的外部加载下进行).在2.0 MN的外部加载下,叶腊石体中心的压力约为2.55 GPa,卸压后测量叶腊石立方体的边长为28.1 mm(实验均在高于1.7 MN的外部加载下进行).由于测量压力梯度的试验中外部加载不会超过7.3 MN,所以叶蜡石立方体的边长在卸压后大于27.9 mm;由于实验过程中叶腊石腔体压力均超过了2.55 GPa(对应外部加载超过了2.0 MN),所以叶蜡石立方体的边长卸压后小于28.1 mm.如图2所示,为了保持顶锤与叶腊石压腔表面中心标压物质绝缘,将一厚约为0.6 mm的叶腊石薄片置于压腔表面,在2.0—7.3 MN的外部加载下,卸压后叶腊石薄片的厚度变为0.5 mm.结合以上测量数据,本文中加压后叶腊石表面中心到体心的距离可表示为(28/2−0.5)mm=13.5 mm.卸压后叶蜡石传压介质立方体的边长会有微小的增加,分析表明,由此而引起的实验误差小于1.1%［25].

4 实验结果讨论

六面顶压机加载过程中,六个顶锤挤压传压介质使部分传压介质分布到六个顶锤之间充当密封边,此过程传压介质及密封边区域均以塑性形变为主,这个过程末的腔体压力可达到约2 GPa,我们把这个过程称为阶段一.继续对压腔系统加压,密封边受到挤压且伴随少量流动而变薄,与此同时压腔体积也会变小,此过程只有少量传压介质流到顶锤之间充当密封边,压腔传压介质区域以弹性变形为主,密封边区域弹性变形与塑性形变同时存在,这个过程末的腔体压力可达到约5 GPa,我们把这个过程称为阶段二.之后,密封边停止流动,传压介质及密封边均以弹性变形为主,由于密封边已经很薄且基本不再流动,致使继续增加外部加载也难以推动顶锤继续前进对压腔区域施加压力,这个过程末的腔体压力最高可达到约6 GPa,我们把这个过程称为阶段三.如图1所示,六面顶压机加载过程中外部加载主要消耗在密封边与合成腔体两个区域,由于压腔表面的压强已经被标定且压腔表面的压力分布基本均匀(压力标定实验结果见图8),作用在压腔表面的加载力大小可用公式表示为

因在高压下作用在立方压腔的每个顶锤形成4个密封边(图1为剖面示意图,只给出了2个密封边),且作用在每个密封边上的力的大小相等,所以作用在密封边区域总的加载力大小可以用公式表示为

式中,F1为作用在合成腔区域的加载力,其中,P为立方压腔表面的压强,S为顶锤作用面面积(23.5 mm×23.5 mm);F2,F3为作用在单个密封边的加载力;Fs为作用在密封边区域总的加载力;F为外部总加载力.

图10为六面顶立方压腔密封边、合成腔体的受力与外部加载的关系.实验分析结果表明,随着外部加载的增加,消耗在立方压腔密封边上的加载急剧上升(曲线斜率变大),与此同时,消耗在合成腔体的加载增加缓慢(曲线斜率变小).腔体压力达到6 GPa之后,所增加的外部加载大部分都消耗在密封边区域,致使腔体压力增加缓慢,继续增加外部加载会达到硬质合金的屈服强度而使顶锤碎裂导致实验失败.我们的实验给出了六面顶压机立方压腔的压力难以超过7 GPa的原因.

图10 (网刊彩色)六面顶立方压腔密封边和合成腔体的受力与外部加载的关系Fig.10.(color online)Relation of the press load allocated to the anvil face and the gaskets versus the total press load.

为了提高立方压腔的压力,首先要找出提高腔体压力的途径,为此我们提出了六面顶压机立方压腔增压的理论模型［26],找到了提高六面顶压机立方压腔压力的途径.由上文分析可知,从阶段三开始,腔体传压介质区域以弹性形变为主,立方压腔的压力增加量可以表示为

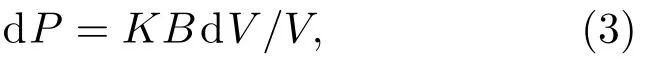
其中,dP为压腔区域的压力增加量;K为压腔系统常数,其大小与加压系统的顶锤硬度、几何尺寸等有关;B为传压介质的体弹模量;dV为压腔传压介质的体积在外部加载力作用下的减小量;V为压腔传压介质体积［30].

如图1所示,腔体传压介质可分为样品区域与密封边区域,样品区域的压力增加量可表示为

密封边区域的压力增加量可表示为

式中B1和B2分别为样品区域传压介质和密封边区域密封边的体弹模量,dV1为样品区域传压介质的体积在外部加载力作用下的减小量,V1为样品区域传压介质体积,dV2为密封边区域传压介质的体积在外部加载力作用下的减小量,V2为密封边区域传压介质的体积.由于六面顶压机的6个顶锤前进距离有限,导致立方压腔的体积变化量不大(见图1),无法通过一直压缩立方压腔的体积而产生更高的压力,从(3)—(5)式可知,除了通过减小传压介质的体积来提高腔体压力,还可得到提高立方压腔压力的另一有效途径,可选用体弹模量相对高的材料作为传压介质来提高样品腔区域的压力dP1;与此同时,可选用体弹模量相对低的材料作为密封边来降低dP2,另外,顶锤的硬度及压腔系统的几何尺寸也是影响样品腔体压力的关键因素(可以改变(3)—(5)式中系数K值),也可以通过选用硬度更高的顶锤和设计更佳的压腔几何尺寸来提高样品腔的压力.我们以此模型为基础,分别设计了叶腊石与氧化镁混合组装及顶锤-预密封边加压系统,将六面顶压腔的最高压力从6 GPa提升至约9 GPa［24,26].以上六面顶压机立方压腔增压的理论模型,可推广至正四面体压腔和正八面体压腔.

图11所示为立方压腔表面中心压力及腔体中心压力与外部加载的关系.由图11可知,在相同加载下叶腊石传压介质表面中心的压力要明显高于叶腊石传压介质体中心的压力,这种差距随着外部加载力的增加而增加.在相同加载下,由表面中心的压力(Ps)减去体中心的压力(Pc)和表面中心与体中心的距离(L)之比,可以得到传压介质内的压力梯度.用公式可表示为

(6)式中G表示沿传压介质对称轴的压力梯度.如果以传压介质表面中心的压力作为横坐标,以压力梯度作为纵坐标,可以得到腔体内对称轴压力梯度与腔体压力(样品腔表面中心的压力)的对应关系.

图11 (网刊彩色)腔体压力与外部加载的关系,a代表传压介质表面中心的压力与外部加载的关系,b代表传压介质体中心的压力与外部加载的关系Fig.11.(color online)Relation of the cell pressure versus the press load.The line a represents the values obtained from the wire at the center of the cube.The line b represents the values obtained from the wire on the face of the cube.

图12 沿着立方体叶腊石传压介质对称轴的压力梯度与腔体压力(样品腔表面的压力)的对应关系Fig.12.Relation of the pressure gradient along the axis of symmetry of the pyrophyllite cube versus cell pressure(pressure on the face of the cube).

图12所示为沿着立方压腔对称轴的压力梯度与腔体压力的对应关系.由图12可知,压腔内沿对称轴的压力梯度随着腔体压力的增加而增加.压腔内传压介质表面中心的压力已知(见图11),且沿压腔对称轴的压力梯度分布基本均匀(见压力标定实验结果图9),那么沿立方压腔对称轴在某一点的压强用公式可表示为

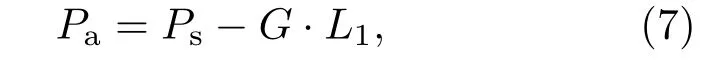
其中,Pa为沿立方叶腊石压腔对称轴在某一点的压强,Ps为立方压腔表面中心的压强,L1为卸压后该点距表面中心的距离.由于高压实验中样品合成腔体沿立方压腔的对称轴设计,该测量方法可为高压实验提供精确的压力数据.此方法不仅适用于叶腊石传压介质,还可推广至氧化镁、三氧化二铝等固体传压介质中.

5 结 论

本文通过标定六面顶立方压腔顶锤表面的压力并结合计算,得到了压腔密封边、合成腔体的受力与外部加载的关系.解释了六面顶压机立方压腔的压力难以超过7 GPa的原因,给出了提高六面顶立方压腔内压力的可行方案.通过定量标定叶腊石立方压腔轴向的压力梯度,给出了一级压腔内不同位置压力值的计算方法,此方法可为高压实验提供更精确的压力标定数据.

[1]Irifune T,Kurio A,Sakamoto S,Inoue T,Sumiya H 2003Nature421 599

[2]Qin J Q,He D W,Wang J H,Fang L M,Lei L,Li Y J,Hu J,Kou Z L,Bi Y 2008Adv.Mater.20 4780

[3]Tian Y J,Xu B,Yu D L,Ma Y M,Wang Y B,Jiang Y B,Hu W T,Tang C C,Gao Y F,Luo K,Zhao Z S,Wang L M,Wen B,He J L,Liu Z Y 2013Nature493 385

[4]Xu C,He D W,Wang H K,Guan J W,Liu C M,Peng F,Wang W D,Kou Z L,He K,Yan X Z,Bi Y,Liu L,Li F J,Hui B 2013Int.J.Refract.Met.Hard.Mater.36 232

[5]Oganov A R,Ono S 2004Nature430 445

[6]Ma Y M,Eremets M,Oganov A R,Xie Y,Trojan I,Medvedev S,Lyakhov A O,Valle M,Prakapenka V 2009Nature458 182

[7]Hemley R J,Soos Z G,Han fl and M,Mao H K 1994Nature369 384

[8]Wang H K,He D W,Xu C,Deng J R,He F,Wang Y K,Kou Z L 2013Acta Phys.Sin.62 180703(in Chinese)[王海阔,贺端威,许超,邓佶瑞,何飞,王永坤,寇自力 2013物理学报62 180703]

[9]Wang H K,He D W,Xu C,Guan J W,Wang W D,Kou Z L,Peng F 2013Chin.J.High Press.Phys.27 0633(in Chinese)[王海阔,贺端威,许超,管俊伟,王文丹,寇自力,彭放2013高压物理学报27 0633]

[10]Dubrovinsky L,Dubrovinskaia N,Prakapenka V B,Abakumov A M 2012Nat.Commun.3 1163

[11]Jayaraman A 1986Rev.Sci.Instrum.57 1013

[12]Andrault D,Fiquet G 2001Rev.Sci.Instrum.72 1283

[13]Klotz S,Besson J M,Hamel G,Nelmes R J,Loveday J S,Marshall W G,Wilson R M 1995Appl.Phys.Lett.66 1735

[14]Fan D W,Wei S Y,Xie H S 2013Chin.Phys.B22 010702

[15]Liebermann Robert C,Wang Y B 1992High-Pressure Research:Application to Earth and Planetary Sciences(Washington DC:AGU)p19

[16]Tange Y,Irifune T,Funakoshi K 2008High Press.Res.28 245

[17]Kunimoto T,Irifune T 2010J.Phys.:Conf.Ser.215 02190

[18]Sung C M 1997High Temp.High Press.29 253

[19]He D W,Wang H K,Tan N,Wang W D,Kou Z L,Peng F 2010Chinese Patent ZL201010142804.7(in Chinese)[贺端威,王海阔,谭宁,王文丹,寇自力,彭放 2010中国专利ZL 201010142804.7]

[20]WangHK,HeDW2011ChinesePatentZL201110091480.3(in Chinese)[王海阔,贺端威 2011中国专利ZL 201110091480.3]

[21]Li Z C,Jia X P,Huang G F,Hu M H,Li Y,Yan B M,Ma H A 2013Chin.Phys.B22 014701

[22]Yu G,Han Q G,Li M Z,Jia X P,Ma H A,Li Y F 2012Acta Phys.Sin.61 040702(in Chinese)[于歌,韩奇钢,李明哲,贾晓鹏,马红安,李月芬2012物理学报61 040702]

[23]Khvostantsev L G 1984High Temp.High Press.16 165

[24]Wang H K,He D W,Tan N,Wang W D,Wang J H,Dong H N,Ma H,Kou Z L,Peng F,Liu X,Li S C 2010Rev.Sci.Instrum81 116101

[25]Wang H K,He D W,Yan X Z,Xu C,Guan J W,Tan N,Wang W D 2011High Press.Res.31 581

[26]Wang H K,He D W 2012High Press.Res.32 186

[27]Fang L M,He D W,Chen C,Ding L Y,Luo X J 2007High Press.Res.27 367

[28]Han Q G,Ma H A,Zhou L,Zhang C,Tian Y,Jia X P 2007Rev.Sci.Instrum.78 113906

[29]Andersson G,Sundqvist B,Backstrom G 1989J.Appl.Phys.65 103943

[30]Daniels W B,Jones M T 1961Rev.Sci.Instrum.32 885

PACS:07.35.+kDOI:10.7498/aps.66.090702

Force analysis and pressure quantitative measurement for the high pressure cubic cell∗

Wang Hai-Kuo1)†Ren Ying1)He Duan-Wei2)Xu Chao3)

1)(Institute of Materials Pressure Treatment,School of Materials Science and Engineering,Henan University of Technology,

Zhengzhou 450001,China)2)(Laboratory of High Pressure Science and Technology,Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China)3)(College of Sciences,Wuhan University of Science and Technology,Wuhan 430065,China)

31 December 2016;revised manuscript

4 February 2017)

Large volume cubic press is one of the most popular high pressure devices which can produce pressures up to about 7 GPa.It is well known experimentally that the enhancing of the maximum pressure generated in the large volume cubic press has attracted wide attention among scientists and engineers because the higher pressure is capable of synthesizing some materials with interesting properties.In the large volume cubic press,pyrophyllite is typically used as a pressure-transmitting medium.A specimen immersed in such a solid experiences a generalized stress state.The pressure distribution in pyrophyllite is an important parameter for characterizing the sample environment and designing the experiments at high pressure.There is a need for the quantitative measurement of pressure gradients in the pyrophyllite pressure medium,so that the accurate experimental data under high pressure can be obtained.

In the large volume cubic apparatus(6×8 MN),we put a circuit into the high pressure cubic cell,so that the pressures at various positions can be measured by using the phase transitions in Bi,Tl and Ba.In the present work,the relationship between the total press load and the press load allocated to the anvil face,and the relationship between the total press load and the press load allocated to gaskets are established at room temperature.The results show that with the increase of the total press load,the load allocated to the gaskets is increased sharply,while the curve of load allocated to the anvil face versus total press load reaches a plateau,which results in the cell pressure reaching upper limit when the cell pressure reaches up to about 5 GPa.According to the experimental results,the stress state of the cubic cell under high pressure is analyzed and the reason why the pressure generated in the large volume cubic chamber is difficult to exceed 7 GPa is explained.Based on the geometrical structure of the cubic cell,the scheme to increase the upper pressure limit for cubic cell by using the material with high bulk modulus as the pressure transmitting medium and the material with low bulk modulus as the gasket,is proposed.Additionally,the method of calculating the pressure values at di ff erent positions along the axis of symmetry in the cubic cell is given through the quantitative calibration of the pressure gradient in the axial direction of the cubic cell.This method can provide more accurate pressure data for high pressure experiments.

high pressure technology,cubic cell,force analysis of the high pressure cell,pressure quantitative measurement

10.7498/aps.66.090702

∗国家自然科学基金青年基金(批准号:11504087,51502217)、河南省教育厅自然科学项目(批准号:14A430033)和河南工业大学科技创新人才项目(批准号:2014CXRC08)资助的课题.

†通信作者.E-mail:haikuo_wang@haut.edu.cn

*Project supported by the National Natural Science Foundation for the Youth Scholars of China(Grant Nos.11504087,51502217),the Natural Science Foundation for Education Department of Henan,China(Grant No.14A430033),and the Fundamental Research Fund for Henan University of Technology,China(Grant No.2014CXRC08).

†Corresponding author.E-mail:haikuo_wang@haut.edu.cn