解三角形的一般方法与策略分析

上海市世界外国语中学 方敏洁

解三角形的一般方法与策略分析

上海市世界外国语中学 方敏洁

笔者在长期的教学实践中发现，许多学生在解三角形这类问题的过程中缺乏系统的思考方法，有时对三角形的转化十分不合理，走了很多弯路。本文现将解三角形的各种情况做出梳理与归纳。

解三角形；合理作高

一、可解三角形的一般解法

一个三角形共有6个基本元素，分别是3条边和3个角，其中至少已知3个元素，且必须已知一条边，此三角形确定了形状大小，那么此三角形的另外三个元素可求，即称此三角形可解。下面举例说明每一种情况下，解三角形的一般方法和步骤：

1.AAS,两角及其对边…………………………………………

【分析】在△ABC中，若已知∠B、∠C是特殊角或其三角比和边AB，那么可过点A作AH⊥BC于H，先解Rt△AHB，再解Rt△AHC。

2.SAS,两边及其夹角

【分析】在△ABC中，若已知∠B是特殊角或其三角比，边AB和边BC，那么可过点A作AH⊥BC于H，先解Rt△AHB，再解Rt△AHC。

3.ASA,两角及其夹边…………………………………………

【分析】在△ABC中，若已知∠B、∠C是特殊角或其三角比和边BC，那么可过点A作AH⊥BC于H，可利用三角比设k表示边C，建立方程求解。

4.SSS,三边

【分析】在△ABC中，若已知边AB、边C和边AC，那么可过点A作AH⊥BC于H，由于AH是公共直角边，可利用勾股定理建立方程求解。

【点评】解斜三角形的本质是通过作高，转化为解两个直角三角形,而添高时要注意不分割已知角。

二、可解三角形的特殊情况的转化

1.在ASA和AAS这两种情况中，若已知的角非特殊角，就不适合过第三个角的顶点作高

【例1】（1）在△ABC中，已知∠B=30°，∠A=15°，边B=2，求边BC和边AC。

（2）在△ABC中，已知∠B=75°，∠A=45°，边AB=2，求边BC和边AC。

（1）ASA

【分析】已知两角及其夹边，但∠A=15°不知其三角比，过C作边AB的高，不可解。可发现30°与15°的和是45°，是特殊角，那么可过点A作AH⊥BC交延长线于H，解△AHB和△ACH。

（2）AAS

【解答】过A作AH⊥BC交延长线于H，

在Rt△ABH中，∠B=30°，AB=2，

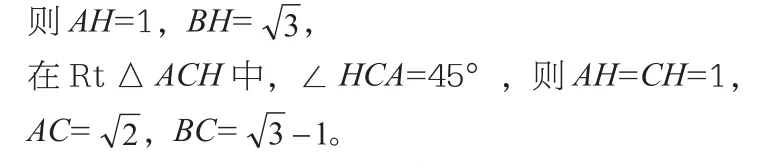
【分析】已知两角及其对边，但∠B=75°，不知其三角比，过A作边BC的高，不可解。可发现75°是30°和45°的和，那么可过B作BH⊥AC交于H，解△AHB和△BCH。

【解答】过B作BH⊥AC交于H，

在Rt△ABH中，∠ABH=30°，AB=2，

【点评】如遇非特殊角，可转换外角为特殊角或分割成两个特殊角。

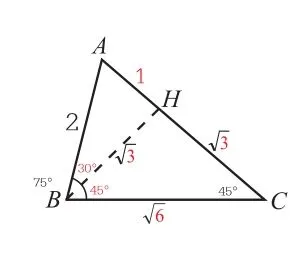
三、合理选择、合理计算

【作图】只需作点C的对应点即可，AC=AC′，且∠CAC′=60°，△ACC′是等边三角形。

【分析】图中有多个可解三角形，如等腰三角形BCC′，30°，75°，75°，腰（需利用75°，计算量大）;等腰三角形BGC′，30°，75°，75°，边未知，得C′B=BG（不可解）;△BGC，30°，，45°（ASA，需引进未知数，解方程）;△BAC′，30°，2，15°（外角45°，可作形外高，最优）。

【解答】将△BCC′孤立出来，如下图所示。

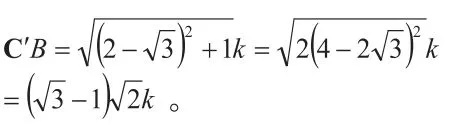
【点评】在复杂图形中，可利用的可解三角形较多，需要进行计算量的评估。一般地，尽可能使用SAS和AAS，因为SSS和AAS需引入未知数，利用公共高建立方程。