一道模考题的解法分析及教学启示

江苏省溧阳市竹箦中学 李华军

一道模考题的解法分析及教学启示

江苏省溧阳市竹箦中学 李华军

高考题、模考题是命题专家经过精心思考、认真打磨才命制出来的，很多试题具有很大的研究空间和教学价值。一道好的试题能充分考查学科的主要知识、常见的解题方法及蕴涵的重要数学思想，本文从一道模考题出发，通过试题各种解法的研究，谈谈对高三数学教学的启示。

一、试题呈现

小值为7。

多元变量求最值问题一直是高考的热点题型，试题形式丰富多变，难度较大，是学生的难点，考试中对此类问题的求解经常出现问题。

二、解法分析

本题解法很多，每一种解法以一个视角为抓手，这种思维的角度能让学生易于上手、顺利解决问题。

视角一：消元视角

“消元”法是处理多元最值问题的最基本方法，通过“消元”将“多元”转化为“一元”函数最值问题是常规的解题策略。需要特别提醒的是：要重视消元后保留元的范围，保留元的取值范围往往不是任意的，有时需要从已知中挖掘隐含条件。

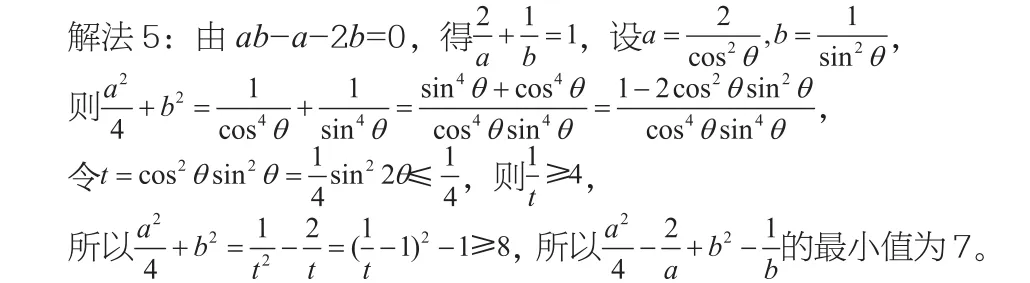
视角三：换元视角

三角代换是常用的一种换元方法，选用适当的三角函数进行换元，将代数问题转化为三角问题，利用三角函数的性质使问题易于解决。

视角二：基本不等式视角

利用基本不等式解决二元最值问题是基本方法，而且作为填空题的压轴题，学生也有意识利用基本不等式来求解，那么构造出符合基本不等式求最值问题的结构是关键。由题目所给条件可得

三、教学启示

1.解题教学要注重方法的提炼

高三数学教学，特别是后期的解题教学，应该注重方法的提炼与熟练。如本题的求解，看到二元变量求最值问题就要想到一般有三个视角可以考虑：一是消元视角，即利用已知方程消去一个未知量，得到单变量的函数形式；二是基本不等式视角，即通过对条件与结论的变形，构造出能运用基本不等式求最值的结构；三是换元视角，通过换元化生题为熟题。

2.解题教学要在思维障碍处引导学生思考

一道试题，学生解的不正确，往往不是对问题全部不理解，而是在某一点出现了思维障碍，如果能跳过这个障碍，很多学生还是能正确解决问题的。本题中很多学生都能想到解法4，但是他们熟悉的是“已知的最小值”题型，现在求的是的最小值，

解题是高中数学学习中的一项重要内容，是高三数学教学的主旋律，高考也是通过解题来考查学生的综合能力和核心素养的。解题教学是否到位，直接影响到学生知识与经验的积累、思维能力的提升、解题能力的培养。实现解题教学效果最大化，提升学生的核心素养是高三数学教学的重要课题。

[1]臧华.一道调研题的多解对二轮复习的启示[J].中学数学研究，2016（6）.

[2]蔡祖才.一道平面向量试题的解法探究与拓展[J].中学数学月刊，2017（5）.