大型冷库内温度场的数值模拟与优化

李艺哲 谢 晶

(上海海洋大学食品学院，上海 201306)



大型冷库内温度场的数值模拟与优化

李艺哲 谢 晶

(上海海洋大学食品学院，上海 201306)

以典型大型冷库作为研究对象，对冷库内外环境(包括空气幕在内)进行三维数值建模，并利用计算流体力学软件对冷库内温度场进行模拟研究，并将计算结果进行了实验验证。通过对结果分析可得：在稳态条件下，库内流场温度虽达到了要求的范围，但堆垛货物附近的温度场分布并不均匀，货物之间与库内其他区域存在着较明显的温差；在非稳态条件下，空气幕的送风速度对温度场的影响很大，当送风速度为8 m/s时，库内温度场的波动较小，空气幕性能较好。在该基础上提出了今后可进一步优化的建议：改变库内空气的流动方式，改变货物的堆垛方式，降低货物堆垛高度，对影响空气幕性能的其他参数进行研究优化。

冷库；温度场；数值模拟；空气幕

近年来，中国冷库在规模和数量上快速增长，但部分冷库内部存在气流分布不均匀的问题，导致了库内食品贮藏质量下降[1-3]。特别是在货物进出冷库时，库内外空气发生强烈热湿热质交换，在库门附近产生薄雾，影响操作人员视线，易引发安全事故[4]，同时还会造成库门处不同程度的结霜、库温升高、热负荷增加等诸多问题[1]。由此可见，冷库运行时库内温度的合理分布至关重要。为了解决上述问题，通常会选择在冷库入口处安装空气幕机来阻隔库内外气体流动交换，进而达到保持库内温度，降低冷库运行能耗的目的[5]，但在使用空气幕的过程中，往往会忽略其送风参数等关键因素，从而影响其封闭、阻隔效果。

计算流体力学(computational fluid dynamics，CFD)是流体力学的分支，常在求解流体流动和传热问题中使用[6]，将CFD软件及数值模拟技术运用在上述问题中，能够快速、直观地模拟出设备内温度场的分布情况，解决流场分布不均匀的问题，还能降低设备能耗；赵鑫鑫等[7]利用CFD软件对影响冷藏车内温度场分布均匀性的因素进行了研究分析；汤毅等[8]利用CFD技术，对3种不同的风机摆设形式进行模拟，分析了它们在运行时对冷库气流的影响，并提出相关节能建议。本研究拟利用计算流体力学(CFD)软件，以及数值模拟理论，对某带货物冷库库内温度场进行稳态模拟研究及实验验证；在此基础上，对库门开启过程中，空气幕在不同吹风速度下库内温度场的变化规律进行研究，从而预测出该冷库空气幕的最佳送风速度，为节约冷库能耗、提高空气幕的运行效率提供参考依据。

1 模型建立

1.1 物理模型

本研究选取上海市杨浦区东方国际水产市场中的典型大型冷库为研究对象，该库尺寸为42 m(长)×36 m(宽)×3.8 m(高)。冷库内使用吊顶排管式蒸发器进行降温，其尺寸为41.2 m(长)×35.2 m(宽)×0.08 m(高)。冷库门位于中间，尺寸为2.4 m(长)×1.8 m(高)。冷库壁面采用0.15 m厚的保温隔热层。库内货物分为四垛摆放，货物之间的通道宽度为4 m。库门外侧上方安装的是贯流空气幕机，距离墙面0.15 m。在计算过程中，库外环境也需要考虑在内，因此本试验将库外过道模拟为38 m(长)×26 m(宽)×4.8 m(高)的长方体。冷库内部、空气幕及库外环境的三维模型见图1。

图1 冷库模型

1.2 数学模型

首先建立合适的描述库内流动换热的数学模型，并在建模时作如下假设：① 库内为不可压缩空气，且符合Boussinesq假设；② 库内管道及铁架对流场的影响忽略不计。由于本模型流场雷诺数约为106，属于大空间紊流流动换热问题，因此可采有D.B.Spalding的紊流流场k-ε的数学模型[9]，在坐标系下，联立连续性方程、能量守恒方程、动量守恒方程、k方程以及ε方程作为计算方程组，5个控制方程表述[10]：

连续性方程：

(1)

能量守恒方程：

(2)

动量守恒方程：

(3)

(4)

(5)

标准的k-ε方程：

(6)

(7)

式中：

Gk——湍动能k的产生项；

Gb——由浮力引起的生成项；

C1ε——常数，1.44；

C2ε——常数，1.92。

2 模拟计算与实验验证

模拟中使用CAD和GAMBIT软件进行模型建立及网格划分，并在FLUENT软件中设定边界条件：对蒸发器采用恒温壁面，t=-24 ℃；对于冷库壁面采用第二类边界条件，壁面总热阻为5.193，库内外设计温度分别为-23，20 ℃，因此可求得壁面的热流密度q=7.68 W/；对货物采用多孔介质模型，货物要求达到的温度范围为-18 ℃左右；货物孔隙率设置为0.6。空气幕回风口采用outflow边界条件：在库门关闭时，采用SIMPLEC算法来求解压力、速度的耦合；当库门开启时，由于是一个瞬态过程，因此采用计算精度更高的PISO算法[11]。

实验验证过程中，温度数据的采集是基于有源RFID技术的库房温度监控系统(自主开发)，测温点的布置方式以排管蒸发器为基础，在其下方进行均匀布点，布点个数为42，按从左到右，从上到下的顺序依次编号，布点位置及部分编号见图2。在稳态测量过程中，为了全面地观测库内各处的温度，将采集全部点的温度进行分析。在非稳态测量过程中，由于靠近库门内侧区域的温度场受到的影响最大，因此仅对靠近库门中心位置点(即图2中编号点4)进行测量即可。

图2 测温点分布图

3 库内稳态温度场结果分析

模拟计算过程中，通过Tecplot360(2013)软件将模拟计算结果输出。图3为冷库的整体三维温度场分布图。从图3可以看出，冷库下部温度比上部温度略高，是由于蒸发器安装在靠近库顶侧，而下部货物有热量散发所致。图4为z=1.9 m截面温度场分布图，可以直观地反映出堆剁货物的截面温度分布：库内四堆货物的温度分布基本趋于一致，都能够达到-18 ℃的要求。图5是冷库堆垛货物间通道纵截面温度场分布图，与图4综合对比可发现，库内每堆货物间通道的温度要明显低于货物本身的温度，而库内其他空间的温度则更低，主要原因是货物在降温时也伴随着热量的散发，而库内的空气流动方式是自然对流，货物间的空气流动较慢，温度较高。图6为z=3.32 m的截面温度场分布图，由图6可知，货物上方的整体温度分布基本均匀。图7是通过CFD软件对截面进行后处理的冷库测温布点截面温度分布图，从图7可以清晰看出，各个测温点的模拟温度值基本一致，所有点都达到了-23 ℃左右。

试验过程中温度的测量是在冷库关门后温度稳定的情况下测得的。图8为模拟结果与试验结果测温点温度值的对比，通过对42个测温点温度值对比发现，模拟结果中各点温度分布基本一致，偏差几乎不存在，温度分布也较均匀，试验结果中则反映出各点之间存在着2～3 ℃的温差。将模拟与试验结果综合比较发现，模拟结果与试验结果仅存在10%以下的较小误差，因此可得模拟结果与试验结果基本相符，数值模拟结果较准确。

图3 冷库三维温度场分布图

图4 冷库z=1.9 m的截面温度场分布图

图5 冷库内通道截面温度场分布图

图6 冷库z=3.32 m的截面温度场分布图

图7 冷库测温布点截面温度分布图

图8 模拟与试验测温点温度对比图

4 空气幕送风速度的优化

在库门开启进出货物时，空气幕的送风速度大小直接影响其封闭效果，若送风速度过小，冷库库门得不到完全封闭，达不到阻隔库外热空气侵入的效果；若速度过大，则导致空气幕运行能耗大，造成不必要的浪费。库内外温度场的变化趋势直接反应了空气幕效果的好坏。因此，在非稳态模拟过程中，将冷库稳态温度场作为初始条件，研究空气幕以不同送风速度开启后，库内外温度场的变化情况，对空气幕的送风速度进行优化。

空气幕送风角度为0°时，送风速度分别为6，8，14 m/s时冷库内外温度场的模拟截面图见图9～11。

由图9可知，1～3 min时，库内温度场由库门向内不断变化，特别是在靠近库门区域受到的影响较大，门内侧附近区域温度高达10 ℃左右，门外侧下方环境温度也在不断变化，由此可见库门处的热量交换比较剧烈，主要原因是空气幕的送风速度过小，射流没有到达库门底部就被破坏，没有起到阻隔外界热量侵入的作用。

由图10可知：当送风速度为8 m/s时，虽然库内温度变化不断向库内部延伸，但库门处的温度有明显的下降，库门内侧上下区域的温度差也有所减小，空气幕的封闭效果得到显著改善，库内温度场基本达到运行要求。

由图11可知，当送风速度增大至14 m/s时，库门附近的温度又有明显的上升，而且库门附近区域温度差也在逐渐增大，空气幕的封闭性能有所下降，这是由于过大的送风速度会造成库内的冷空气与空气幕射流之间的热质交换增加，导致库外热空气大量向库内侵入。

图12为空气幕在3种不同送风速度下，库内测温点的变化趋势图。由图12可知，当空气幕的送风速度为8 m/s时，库内测温点的值达到最低，且与模拟结果完全一致。因此可得，此冷库空气幕的最佳送风速度为8 m/s。

图9 冷库内外温度场y轴中心截面图(6 m/s)

图10 冷库内外温度场y轴中心截面图(8 m/s)

图11 冷库内外温度场y轴中心截面图(14 m/s)

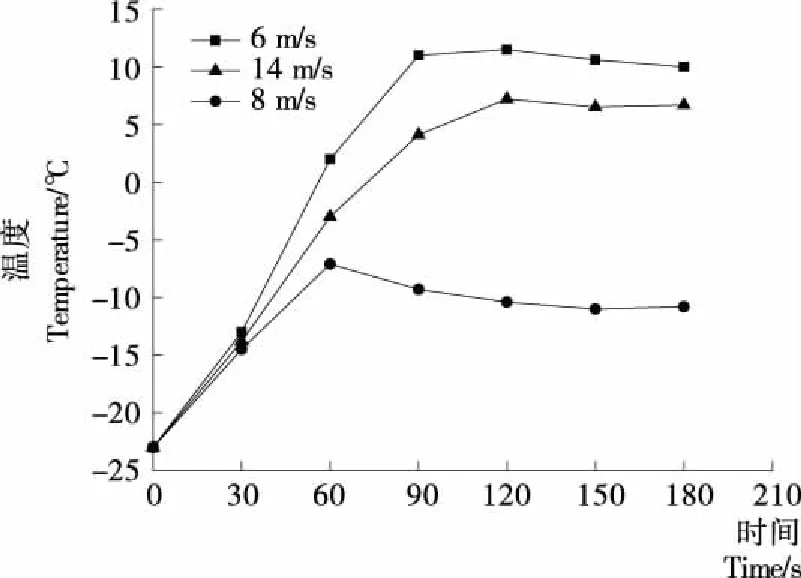
图12 冷库内测温点4温度变化图

5 结论

通过对堆垛货物冷库内部温度场实测发现：库内流场温度虽达到了要求，但堆垛货物附近局部温度场分布还有不足。本研究对象冷库面积较大，库内空气流动速度较慢，从而影响库内温度场的分布。在对空气幕参数优化的研究中，虽得到空气幕的最优送风速度，使空气幕的封闭性能得到增强，但在实际应用方面，空气幕的其他参数对其隔离效果也起着关键作用，不容忽视。因此，在今后的研究中可考虑以下几点建议：

(1) 改变库内空气的流动方式，在堆垛货物之间的通道尽头两端加装风机，加快库内及货物之间的空气流动，减小库内不同区域的温差。

(2) 改变货物的堆垛方式。由于货物的摆放形式对库内流场分布产生重要的影响，因此可以减小堆垛货物尺寸，增加货物堆垛数量，使货物之间有更多的间隙，从而使库内空气流动更均匀。

(3) 降低货物堆垛高度。适当降低货物堆垛高度，增加每层货物的间距，能够促进货物间空气的流动，使货物温度均匀。

(4) 还可以对影响空气幕封闭效果的其它参数(送风温度、送风角度、喷口宽度)进行优化，使空气幕的各项参数达到最优，进一步增强空气幕的性能、降低空气幕的运行能耗。

[1] 谢晶, 吴天. 小型冷库开关门过程温度场的数值模拟[J]. 上海海洋大学学报, 2006, 15(3): 333-339.

[2] 杨磊, 汪小旵. 冷藏库预冷降温过程中温度场的数值模拟与试验研究[J]. 西北农林科技大学学报: 自然科学版, 2008, 36(9): 219-223.

[3] 刘妍玲, 张岩, 王世清, 等. 果蔬摆放形式对冷库内气流场分布影响的研究[J]. 青岛农业大学学报: 自然科学版, 2008, 25(1): 24-27.

[4] 缪晨, 谢晶. 空气幕的研究进展[J]. 食品与机械, 2012, 28(4): 237-240, 262.

[5] 缪晨, 谢晶. 冷库空气幕流场的非稳态数值模拟及验证[J]. 农业工程学报, 2013, 29(7): 246-253.

[6] 谢晶, 瞿晓华, 施骏业. 计算流体力学在食品工业中的应用[J]. 上海海洋大学学报, 2004, 13(2): 170-175.

[7] 赵鑫鑫, 王家敏, 李丽娟, 等. 多温区冷藏车回风导轨对厢内温度场的影响分析[J]. 食品与机械, 2014, 30(1): 149-154.

[8] 汤毅, 谢晶, 王金锋, 等. CFD 预测风机摆设形式对冷库的影响[J]. 食品与机械, 2012, 28(1): 124-128.

[9] 张登春, 陈焕新, 舒信伟, 等. 空调车内三维紊流流动与传热的模拟研究[J]. 铁道学报, 2002, 24(6): 39-43.

[10] 吕全立, 林金庭, 陈效建, 等. 异质结构的流体动力学输运模型及其在HBT一维分析中的应用[J]. 固体电子学研究与进展, 1994(2): 108-115.

[11] 王彤, 谷传纲, 杨波, 等. 非定常流动计算的 PISO 算法[J]. 水动力学研究与进展, 2003, 18(2): 233-239.

Numerical simulation and optimization on temperature field in large cold store

LI Yi-zhe XIE Jing

(College of Food Science and Technology, Shanghai Ocean University, Shanghai 201306, China)

A three-dimensional numerical model included the inside and outside environment of the cold store, and air curtain of the big cold store was established in this study. The steady and unsteady simulations of the temperature field were performed by using numerical simulation software, and the relative results were used for experimental verification. It turned out that experimental verification was basically coincidence with the results of the simulations. Acquired from analyzing the results of simulations, although the temperature field in the cold store reached the required temperature range, the distribution of temperature field near stacking goods was not balance completely, due to the obvious temperature difference between goods and other areas in the cold store. When the supply velocity of the air curtain was 8 m/s under the unsteady condition, the temperature field of the cold store had the smallest fluctuation and the air curtain had the highest efficiency. We put forward suggestions that it could be optimized in future, including the change of air flow patterns in a cold store, the stacking ways and height of goods, and other parameters of the air curtain.

cold store; temperature field; numerical simulation; air curtain

国家“十三五”重点研发项目(编号：2016YFD0400303)；上海市科委平台能力提升项目(编号：16DZ2280300)

李艺哲，男，上海海洋大学在读硕士研究生。

谢晶(1968—)，女，上海海洋大学教授，博士。 E-mail：jxie@shou.edu.cn

2017—03—09

10.13652/j.issn.1003-5788.2017.06.028