基于密切值法的RV减速器传动受力影响分析

郑钰馨,奚 鹰,李梦如,卜王辉,华滨滨,柳先辉

(同济大学 a.机械与能源工程学院; b.电子与信息工程学院,上海 201804)



基于密切值法的RV减速器传动受力影响分析

郑钰馨a,奚 鹰a,李梦如a,卜王辉a,华滨滨a,柳先辉b

(同济大学 a.机械与能源工程学院; b.电子与信息工程学院,上海 201804)

在对RV减速器结构简化的基础上,根据齿轮啮合原理,采用相对运动法进行了减速比计算,详细阐述了摆线轮与无针齿套针齿啮合受力分析方法.在此基础上,使用密切值法,进行了多种参数对RV传动受力影响程度分析,确定了摆线轮厚度、曲柄轴偏心距以及针轮滚针半径为与受力密切相关的参数,在RV结构尺寸优化中首先考虑将这三者作为设计变量.

RV减速器; 减速比计算; 啮合受力分析; 密切值法

RV减速器是摆线针轮减速器的一种,具有二级减速机构,一级为渐开线圆柱直齿轮传动机构,二级为双摆线针轮传动,具有传动效率高、精度高、传递扭矩大、传动平稳、体积小、质量轻的特点,适用于精密和重载机器人.但是,其制造工艺复杂,关键技术严格保密,所以RV减速器的发展较为缓慢,成为制约工业智能化发展的关键因素.目前,在国外主要有两个研究小组,分别是美国的休斯飞机公司的Blanche[1]和日本山口大学的日高照晃[2-3].国内,李力行、何卫东、关天民等对RV减速器进行了详细研究,文献[4-5]提出了摆线轮修型方法和摆线轮修型后受力分析方法,文献[6]提出有效影响摆线针轮行星传动承载能力3参数为偏心距、针齿套半径以及针齿销半径,针对这3个变量提出了以输出轴的定额转矩T最大的目标函数.文献[7]对传动部分和行星架输出机构的误差影响因素进行了分析,得到传动误差综合公式.文献[8]对RV减速器整体施加角速度-ωh后,进行了减速比计算,提出了在力平衡和力矩平衡条件下的摆线轮、曲柄轴以及输出轴的受力方程,并计算了RV减速器传动效率,证明了RV传动效率大于单级无针齿套摆线传动效率.文献[9]指出了RV减速器和普通摆线针轮减速器在针齿结构上的不同,提出了适用于RV减速器摆线针轮受力的分析方法.这些理论研究为RV减速器的发展打下了结实的基础.

本文在此基础上,基于齿轮啮合原理,首先，根据几何关系,采用相对运动法对RV减速器减速比进行了计算,与文献[8]中反转法相比,此方法更加直观易于理解,但分析比较繁琐,可以作为反转法的对比验证方法;其次,详细阐述了无针齿套RV减速器摆线轮啮合受力计算方法,并对RV-40E型减速器进行了计算;最后,使用密切值法对多参数进行了啮合力影响程度排序,为RV减速器的优化设计提供设计变量选择依据.

1 RV-40E减速器传动分析

1.1 RV-40E减速器机构简化

RV-40E减速器结构简图如图1所示,两个相同的摆线轮互为180°布置,用来平衡摆线轮传动的偏心惯性力.两个相同的曲柄轴,以及曲柄轴一端固结的行星轮,用来均分曲柄轴承受的载荷.

图1 双曲柄轴RV-40E传动结构简图

1.2 RV-40E减速器的减速比分析

减速比就是输入轴1的转速ω1与输出轴5的转速ω5之比.图2中,摆线轮3与输出轴5之间的连接机构称为“W机构”,即摆线轮3的绝对角速度ω3与输出轴5的转速ω5相等.

由A点处的速度关系

有

(1)

式中:ω2r5为曲柄轴与行星轮固结件2相对于输出轴5的转动角速度.

由B点处的速度关系

有

(2)

图2 RV-40E减速比分析图

式中:R1，R2分别为输入轴中心轮1和行星轮2的半径.

由于ω3=ω5,得到

(3)

因为a+b+c=R6,b=R6-R3,其中R6和R3分别为针轮6和摆线轮3的半径,所以得到

(4)

根据齿轮啮合原理

有

(5)

式中：Z1和Z2分别为输入轴中心轮1和行星轮2的齿数.

(6)

式中：Z6和Z3分别为针轮6和摆线轮3的齿数.

有

(7)

这款RV-40E减速器的参数为Z6=40,Z1=10,Z2=26,Z3=39,因此得

(8)

即,这款RV-40E减速器的减速比为105.

2 RV-40E减速器摆线轮啮合受力分析

2.1 RV-40E减速器基本参数

RV-40E减速器相关具体参数如下:针齿中心圆半径rz=64 mm,针齿半径rrp=3 mm,针轮壳内径rp=70 mm,偏心距e=1.3,针轮齿数zp=40,摆线轮齿数zc=39,中心轮齿数z1=10,行星轮齿数z2=26,模数m=1.25,压力角α′=20°,中心轮转速v1=525r/min,单片摆线轮扭矩Tc=314.6N·m,输出转速为v2=5r/min,速比i=105,输出转矩为T=572N·m,摆线轮弹性模量E=2.07×105N/mm2,泊松比μ=0.254,针齿E=2.08 ×105N/mm2,泊松比μ=0.3,外壳弹性模量E=1.68 ×105N/mm2,泊松比μ=0.24,摆线轮厚度bc=8.86mm.

2.2 RV-40E摆线轮与针齿啮合受力分析

标准摆线轮以及只经过转角修型的摆线轮与标准针轮啮合,在理论上可以达到同时啮合的齿数为摆线轮齿数的一半,但摆线轮齿型经过等距、移距或等距加移距复合修形,如果不考虑零件弹性变形补偿作用,则只能存在一个齿啮合,其余的摆线轮轮齿与针齿之间都存在着大小各不相同的初始间隙,其啮合法线方向的初始间隙Δ(φi)根据文献[7-8]计算如下:

(9)

式中:φi为第i各针齿相对于转臂的转角(°),0≤φi≤180°;k为短幅系数,k=ezp/rz=0.812 5;a为移距修型量(mm),a=0.008;b为等距修型量(mm),b=-0.002;e为曲柄轴偏心距,e=1.3 mm.

由于RV-40E的针轮为40个齿,所以360/40=9,即每9°分布一个齿,如图3所示.

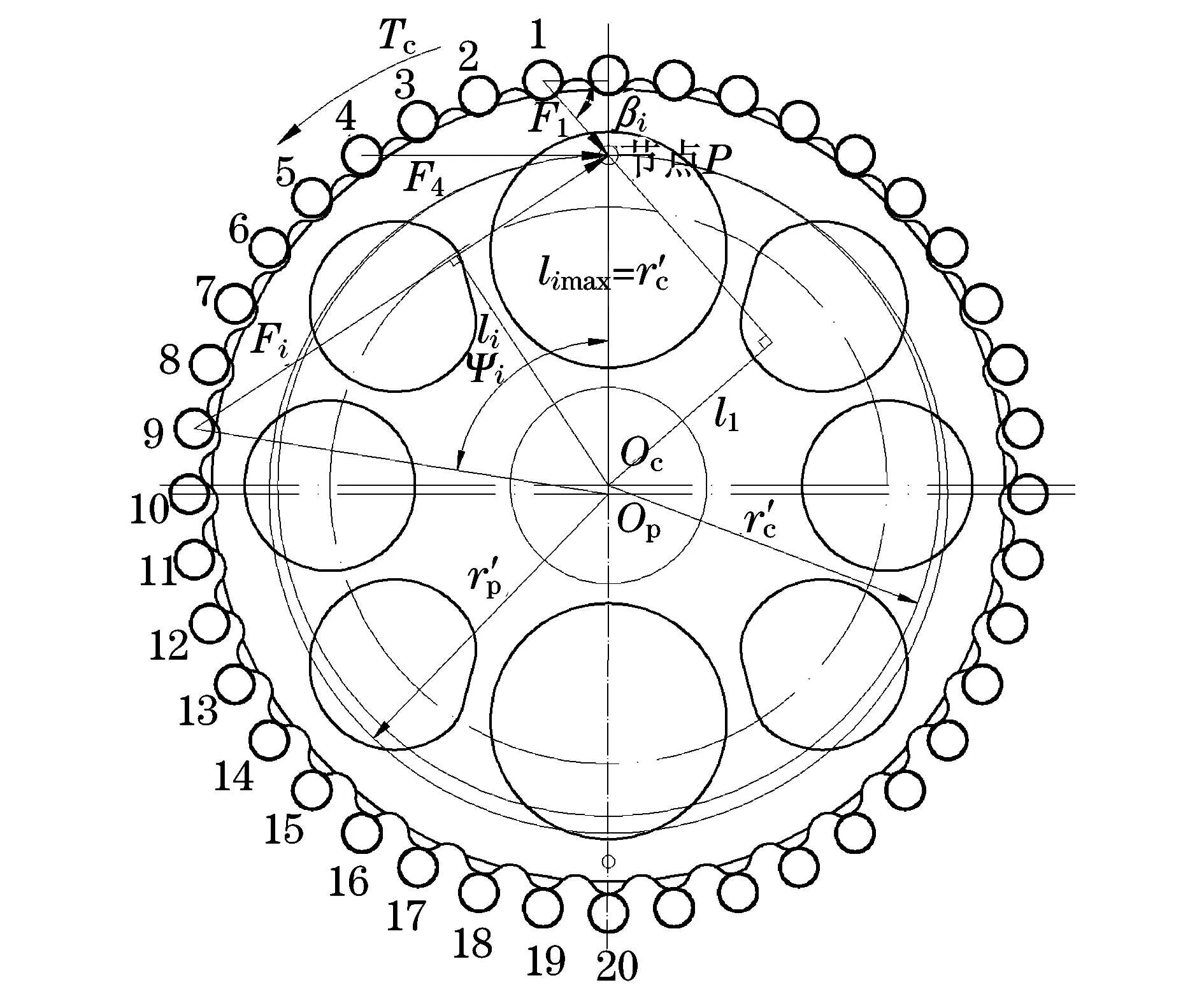
图3 摆线轮啮合受力图

但考虑弹性变形情况下,对摆线轮施加力矩时,摆线轮与针齿会产生接触变形,将接触变形分两部分：一是摆线轮轮齿与针齿啮合时的接触变形ω1;二是针齿与针轮壳之间的接触变形ω2.当这两种变形量大于初始间隙时,就会产生多齿啮合情况.根据RV传动装置的特点,知两者是在相同的啮合力作用下同时产生的,共同影响摆线轮的啮合力大小.根据赫兹公式,长以L(L=bc)的圆柱与圆柱接触时,其接触变形为

式中:F为两圆柱之间的作用力(N);E1,E2为两圆柱的弹性模量(N/mm2);R1,R2为两圆柱的半径(mm);μ1,μ2为圆柱的泊松比.

(11)

当圆柱与圆柱凸凸面接触时,当量曲率半径为

(12)

当圆柱与圆柱凸凹面接触时,当量曲率半径为

(13)

摆线轮实际齿廓曲线的曲率半径为

当摆线轮和针齿接触时,

(15)

当针齿和针轮壳接触时,

(16)

每一个啮合位置同时有两个变形量,所以,ω=ω1+ω2,在求得每个位置的变形量后,得到其中最大变形量ωmax.

在弹性变形条件下,啮合力法向上的位移为

式中:β为加载后由零件变形而引起的摆线轮的转角(°);li为第i个啮合点的公法线或待啮合点的法线至摆线轮中心Oc的距离(mm),如图3所示;r′c为摆线轮的节圆半径(mm),r′c=ezc;δmax为啮合处最大变形量(mm),δmax=ωmax.

当δi-Δ(φ)i>0时,相对应的齿数i啮合,并且其啮合力表达式如下:

式中:Tc为一片摆线轮传递的转矩(N·mm),Tc=0.55T;T为输出轴上阻力矩(N·mm).

最大啮合力的初始值描述如下:

在无间隙、啮合时,最大的啮合力为

(21)

有间隙时、啮合时,最大的啮合力为

(22)

而真正的啮合状态,处于这两者之间,所以,最大初始啮合力大小为

(23)

以式(23)为初值,带入式(9)～(20),得到按照Fmax,并按照下面判别式(24),通过迭代得到更加符合实际的初始值

(24)

通过Matlab编程计算得到,RV-40E减速器的啮合区间为2～11个齿,最大初始啮合力为Fmax=1 284.6N.通过迭代计算后,得到的最大啮合力为1 190.8N,出现在第4个针齿附近,并且,通过(arccsc0.812 5)/9=3.962,可知,最大啮合力的理论出现位置也是第4个齿.

摆线轮接触应力为

(25)

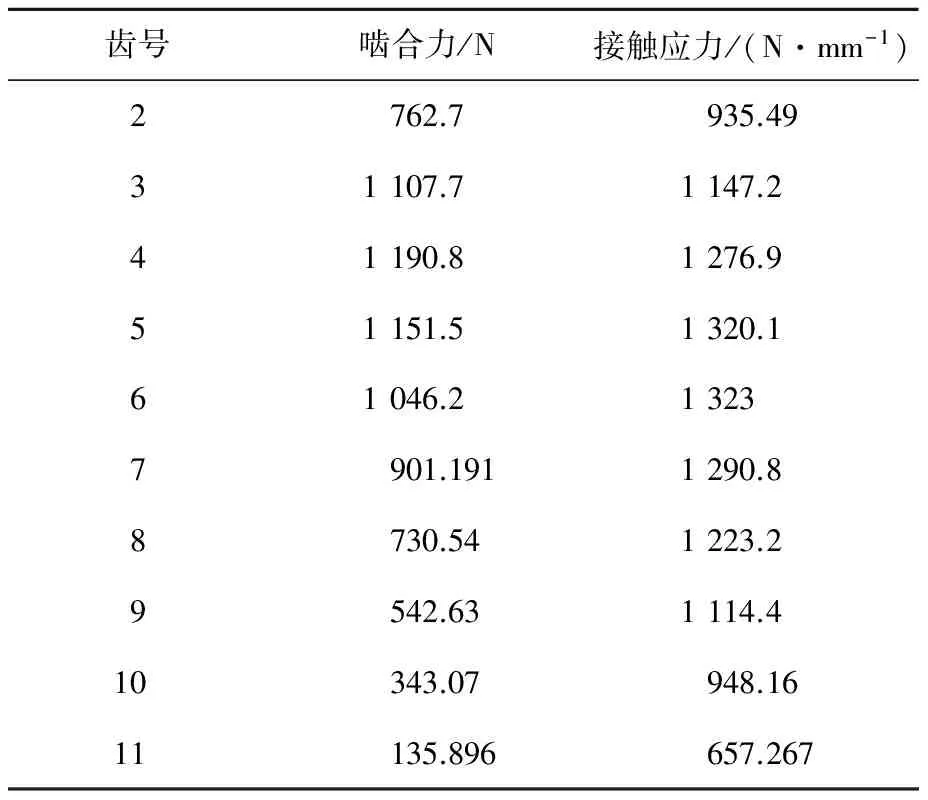
表1 理论计算啮合力和接触应力

2.3 RV-40E摆线轮与针齿啮合合力计算

当Fi与x轴的夹角为βi时,如图3所示,则有

(26)

(27)

(28)

通过计算,Fx=7 422.005 N,Fy=1 245.9 N,Fx,Fy为作用在一个摆线轮上的各针齿啮合力在X,Y方向上的合力.

3 基于密切值法的参数影响系数分析

从式(9)～(28)可知,针轮滚针半径、移距修型量、等距修型量、摆线轮厚度和曲柄轴偏心距是影响摆线轮啮合力大小的重要参数.根据密切值法,要建立n×m的原始指标矩阵,其中n为需要进行排序的参数,m为评价指标.当参数值变化相同数值0.001 mm时,最大啮合力的变化值并不能作为影响程度排序的单一指标,还需将原始值、材料的弹性模量、工艺实现难易程度作为衡量指标,如表2所示.

矩阵模型的规范化后为表3.则最优点集合为

G={0.467 6,0.448 5,0.938 2,0.448 9,0.545 5}

则最劣点集合为

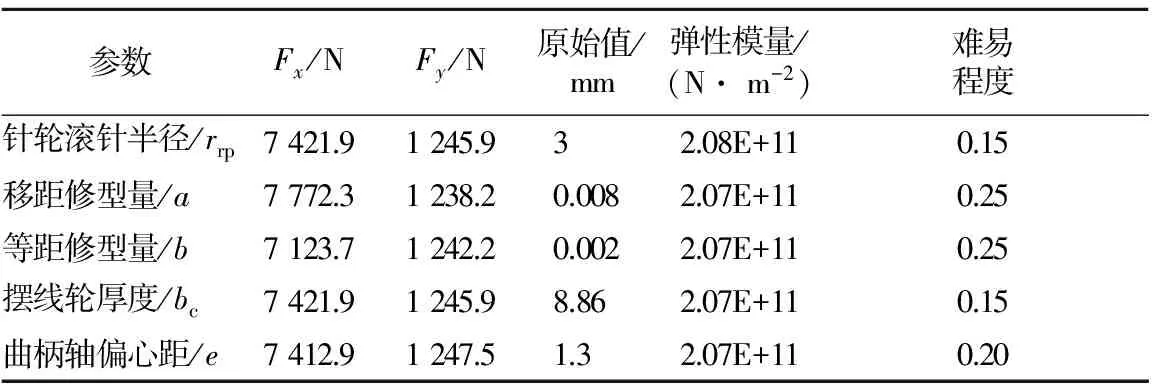
表2 原始指标矩阵

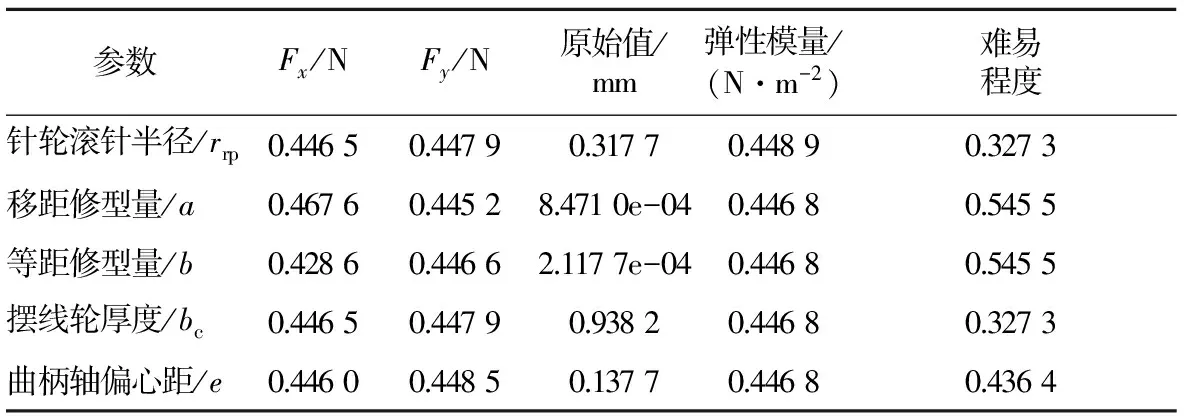
表3 规范化指标矩阵

则各评价单元与最优评价点和最劣评价点的密切系数为表4.

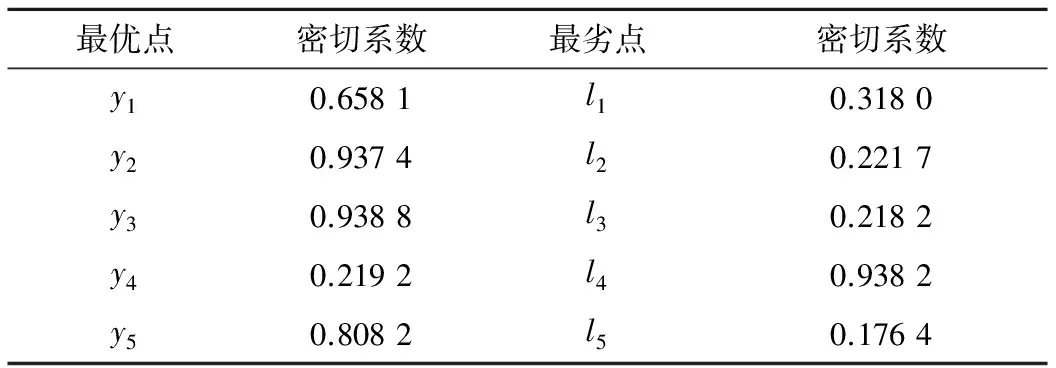
表4 评价单元的密切系数

密切值是无量纲值,以C表示,它以各评价单元与最优点的最小距离和与最劣点的最大距离作为参比,综合比较其隶属于最优点和最劣点亲疏程度.当C值越小,则被评单元与最优点关系越密切,与最劣点关系越疏远.当C=0,被评单元指标值在的所有参评单元中达到最优.通过表5可知,在综合考虑情况下,摆线轮厚度、曲柄轴偏心距以及针轮滚针半径三者对RV减速器受力影响较大,在RV优化设计中,优先考虑这3个参数.

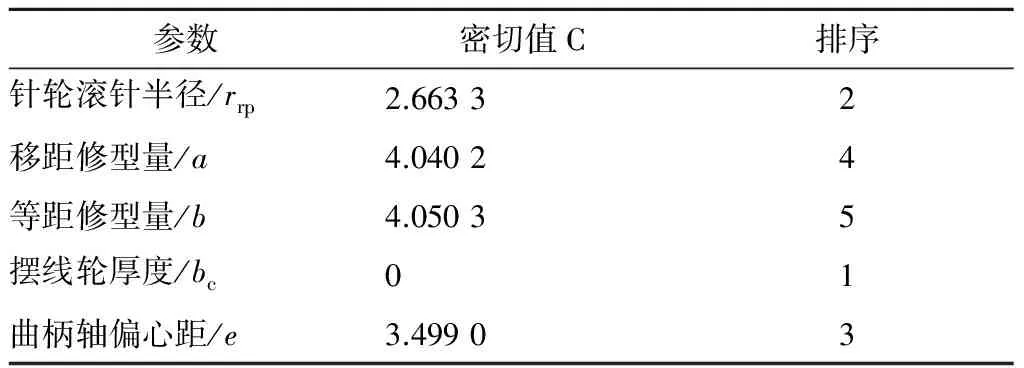
表5 评价单元的密切值及排序

4 结论

(1) 根据齿轮啮合传动原理,使用相对运动法对RV减速器的减速比进行了计算,所得结果与RV-40E实际减速比一致,此方法较为复杂,但相对于反转法更易于理解和掌握.

(2) 进行了摆线轮和无针齿套针齿的啮合受力分析,对RV-40E进行了详细计算,为动力学分析奠定了基础.

(3) 在啮合受力分析基础上,运用密切值法分析了各参数对啮合受力的影响,此方法采用统计学概念,对影响程度进行排序,简单方便可靠,所得结论可以用于RV优化设计中.

[1] BLANCHE J G,YANG D C H.Cycloid drives with machining tolerances[J].Journal of Mechanisms,Transmissions,and Automation in Design,1989,111(9):337-344.

[2] 石田武,王宏猷,日高照晃,ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車装置の回转传达误差に开する研究(第2报,各种加工误差、组立误差が回转传达误差に及ほす影响)[J].日本耭械学会论文集(C编),1994,60(578):278-285.

ISHIDA T,WANG Hongyou,HIDAKA T,et al.Rotational transmission error of K-H-V planetary gears with cycloid gear(2nd report,effects of manufacturing and assembly error)[J].JSME International Journal:Serises C,1994,60(578):278-285.

[3] 日高照晃,王宏猷,石田武,ほか.サィクロィド齿车を用ぃた K-H-V形游星齿车装置の回转连误差に开する研究(第1报:解析方法)[J].日本机械学会论文集(C编),1994,60(570):645-653.

HIDAKA T,WANG Hongyou,ISHIDA T,et al.Rotational transmission of K-H-V plantary gears with cycloid gear(1st report,analytical method of the rotational transmission error)[J].JSME International Journal:Serises C,1994,60(570):645-653.

[4] 李力行.摆线针轮行星传动的齿形修正及受力分析[J].大连铁道学院学报,1984,4:29-39.

LI Lixing.The modification manner for tooth profile and the analysis of forces on the cycloid disk of a cycloid speed reducer[J].Journal of Dalian Institute of Railway Technology,1984,4:29-39.

[5] 李力行,洪淳赫.摆线针轮行星传动中摆线轮齿形通用方程式的研究[J].大连铁道学院学报,1992,13(1):7-11.

LI Lixing,HONG Chunhe.The general equations for the teeth profile of cycloidal gear[J].Journal of Dalian Institute of Railway Technology,1992,13(1):7-11.

[6] 李力行,关天民,王子孚.摆线针轮行星传动的计算机辅助设计[J].大连铁道学院学报,1992,13(1):26-33.

LI Lixing,GUAN Tianming,WANG Zifu.The computer aided design of cycloid gearing[J].Journal of Dalian Institute of Railway Technology,1992,13(1):26-34.

[7] 李力行,何卫东,王秀琦.机器人用高精度RV传动的研究[J].大连铁道学院学报,1999,20(2):2-10.

LI Lixing,HE Weidong,WANG Xiuqi.The study on high-accuracy RV drive used in robot[J].Journal of Dalian Railway Institute,1999,20(2):2-10.

[8] 何卫东,李力行.RV传动的效率及其受力分析[J].大连铁道学院学报,1992,13(1):73-81.

HE Weidong,LI Lixing.Analysis on the forces and efficiency of RV reducer[J].Journal of Dalian Institute of Railway Technology,1992,13(1):73-81.

[9] 何卫东,李力行.机器人用RV传动中摆线轮受力分析[J].大连铁道学院学报,1999,20(2):49-53.

HE Weidong,LI Lixing.Force analysis on cycloidal gear of the RV drive used in robot[J].Journal of Dalian Railway Institute,1999,20(2):49-53.

Original error analysis on the second reduction part of RV reducer

ZHENG Yuxina,XI Yinga,LI Mengrua,BU Wanghuia,HUA Binbina,LIU Xianhuib

(a.School of Mechanical Engineering; b.School of Electronics and Information Engineering,Tongji University,Shanghai 201804,China)

On the basis of RV reducer structure simplification,according to the principle of gear meshing,a relative motion method is used for RV reducer reduction ratio calculation,a meshing force analysis method of cycloid gear with no sleeve pin gear is expounded,and on this basis,using osculating value method,an analysis of various parameters influence on RV transmission force is made,and get a conclusion that the thickness of cycloid gear,the eccentricity of crankshaft and the radius of roller are closely parameters related to the transmission force.In structural optimization,the three parameters are considered as design variables preferentially.

RV reducer; the reduction ratio calculation; meshing force analysis; osculating value method

国家自然科学基金资助项目(51475331);中央高校基本科研业务费专项基金资助项目(20153712);上海市科技创新计划资助项目(15111102702)

郑钰馨(1989—),女,博士生.E-mail:zhengyuxin1989@126.com

TP 242.2

A

1672-5581(2017)02-0153-05