平方s-凸函数的Hermite-Hadamard型不等式
时统业, 李 军
(海军指挥学院 信息系,江苏 南京 211800)
平方s-凸函数的Hermite-Hadamard型不等式
时统业, 李 军
(海军指挥学院 信息系,江苏 南京 211800)
利用s-凸函数与平方s-凸函数的关系,或者从平方s-凸函数的定义出发,建立了平方s-凸函数的Hermite-Hadamard型不等式.
平方s-凸函数;s-凸函数;Hermite-Hadamard 型不等式
0 引言
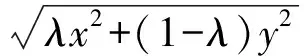
定义2[2]设I⊆[0,∞)为平方凸集,函数f是定义在I上的正值函数,若对任意x,y∈I,λ∈[0,1],有
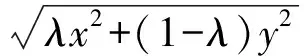
则称f是定义在I上的平方凸(凹)函数.
文献[1,3-4]研究了平方凸函数的性质.文献[5]给出平方凸函数的积分型Jensen不等式.文献[6]建立了平方凸函数的2次幂平均型Hadamard型不等式.
s-凸函数[7-9]、s-预不变凸函数[10]、GA-s-凸函数[11-12]、调和s-凸函数[13]、s-对数凸函数[14-15]、调和平方s-凸函数[16-17]、几何s-凸函数[18-19]、r次幂平均s-凸函数[20]分别是凸函数、预不变凸函数、GA凸函数、调和凸函数、对数凸函数、调和平方凸函数、几何凸函数、r次幂平均凸函数的推广.本文中所指s-凸函数均指第二种意义上的s-凸函数.作为平方凸函数的推广,文献[21]提出平方s-凸函数的概念.
定义3[21]设I⊆(0,∞),s∈(0,1],f:I→(0,∞).若对任意x1,x2∈I和任意t∈[0,1],有
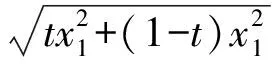
(1)
则称f为I上的平方s-凸函数.若式(1)中的不等号反向,则称f为I上的平方s-凹函数.
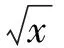
定理1[9]设f:[0,∞)→[0,∞)是第二种意义上的s-凸(凹)函数,s∈(0,1],a,b∈[0,∞),a 定理2[21]设[a,b]⊆(0,+∞),s∈(0,1],f为[a,b]上的平方s-凸(凹)函数,则有 由引理1和引理2立得引理3. 本文的目的是建立平方s-凸函数的Hermite-Hadamard型不等式. 定理3设[a,b]⊆(0,+∞),s∈(0,1],f为[a,b]上的平方s-凸(凹)函数.若f在[a,b]上勒贝格可积,则有 (2) 证明由引理3和定理1得 推论1若f(x)为[a,b]⊆(0,+∞)上的平方凸函数,则有 (3) 证明由平方s-凸函数定义,对任意x,y∈[a,b]有 (4) (5) 由平方s-凸函数定义,对任意x∈[a,b]有 (6) (7) 将式(6)和(7)相加得 (8) 将式(5)和式(8)乘以xp(x),然后对x在[a,b]上积分并注意到 则式(3)得证. 注1在定理4中取p(x)≡1,则得到定理2. 定理5设[a,b]⊆(0,+∞),s∈(0,1],f为[a,b]上的平方s-凸函数.若f在[a,b]上勒贝格可积,则有 (9) (10) 由平方s-凸函数定义,对任意x∈[a,b]有 (11) (12) 将式(11)和(12)相加得 (13) 则式(9)得证. 推论2若f(x)为[a,b]⊆(0,+∞)上的平方凸函数,则有 [1] 赵宇. 半连续函数的平方凸性[J]. 佳木斯大学学报(自然科学版), 2008, 26(6): 842-844. [2] 吴善和. 平方凸函数与琴生型不等式[J]. 首都师范大学学报(自然科学版), 2005, 26(1): 16-21. [3] 白淑萍, 李彦军, 谷桂花. 平方凸函数的几个性质[J]. 内蒙古民族大学学报(自然科学版), 2005, 20(4): 425-427. [4] 陈少元, 宋振云. 平方凸函数的两个充要条件及其应用[J]. 湖北师范学院学报(自然科学版), 2012, 32(2): 63-67. [5] 陈少元, 宋振云. 关于平方凸函数的积分型Jensen不等式[J]. 首都师范大学学报(自然科学版), 2012, 33(6): 1-4. [6] 宋振云, 涂琼霞. 平方凸函数的2次幂平均型Hadamard不等式[J]. 高师理科学刊, 2011, 31(3): 24-26. [7] BRECKNER W W.Stetigkeitsaussagen für eine klasse verallgemeinerter konvexer funktionen in topologischen linearen Räumen[J].Publ Inst Math,1978,23:13-20. [8] HUDZIK H,MALIGRANDA L.Some remarks ons-convex functions[J].Aequationes Math,1994,48:100-111. [9] DRAGOMIR S S,FITZPATRICK S.The Hadamard’s inequality fors-convex functions in the second sense[J].Demonstratio Math,1999,32(4):687-696. [10]李觉友.关于s-预不变凸函数的Hadamard型不等式[J]. 重庆师范大学学报(自然科学版),2010,27(4):5-8. [11]SHUANG YE,YIN HONGPING,QI FENG.Hermite-Hadamard type integral inequalities for geometric-arithmeticallys-convex functions[J].Analysis,2013,33(2):197-208. [12]ISSCAN I.Hermite-Hadamard type inequalities for GA-s-convex functions[J].Le Matematiche,2014,69(2):129-146. [13]NOOR M A,NOOR K I,AWAN M U,et al.Some integral inequalities for harmonicallyh-convex functions[J].University Politehnica of Bucharest Scientific Bulletin-Series A-Applied Mathematics and Physics,2015,77(1):5-16. [14]XI BOYAN,QI FENG.Some integral inequalities of Hermite-Hadamard type fors-logarithmically convex functions[J].Acta Mathematica Scientia,2015,35(3):515-524. [15]NOOR M A,QI FENG,AWAN M U.Some Hermite-Hadamard type inequalities for log-h-convex functions[J].Analysis,2013,33(4):367-375. [16]宋振云.调和平方s-凸函数及其Jensen型不等式[J].数学的实践与认识,2016,46(3):279-284. [17]时统业, 周国辉. 调和h-凸函数和调和平方s-凸函数的Fejér和Hermite-Hadamard型不等式[J]. 湖南理工学院学报(自然科学版), 2016, 29(2): 1-5+12. [18]宋振云.几何s-凸函数及其性质[J].山西师范大学学报(自然科学版),2016,30(1):1-5. [19]时统业, 周国辉. 几何s-凸函数的加权积分不等式[J]. 河南教育学院学报(自然科学版), 2016, 25(4): 1-6. [20]宋振云, 陈少元,胡付高.r次幂平均s-凸函数及其Jensen型不等式[J]. 东北师大学报(自然科学版), 2016, 48(4): 19-23. [21]宋振云. 平方s-凸函数及其性质[J]. 首都师范大学学报(自然科学版), 2017, 38(1): 9-13. Hermite-HadamardTypeInequalitiesforSquares-ConvexFunctions SHI Tongye, LI Jun Based on the relation betweens-convex functions and squares-convex functions, or by the definition of squares-convex functions, Hermite-Hadamard type inequalities for squares-convex functions are established. squares-convex function;s-convex function; Hermite-Hadamard type inequality 2017-03-05 海军指挥学院导师及研究生优质课程资助项目 时统业(1963—),男,河北张家口人,海军指挥学院信息系副教授,主要研究方向:基础数学教学. 10.3969/j.issn.1007-0834.2017.02.001 O178 :A :1007-0834(2017)02-0001-04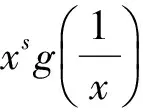
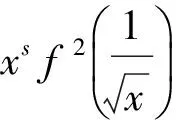
1 主要结果
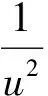
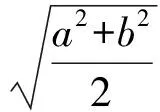
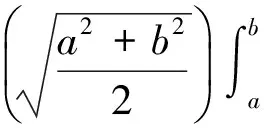
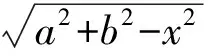
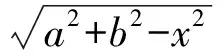
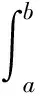
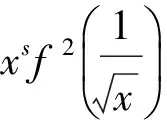
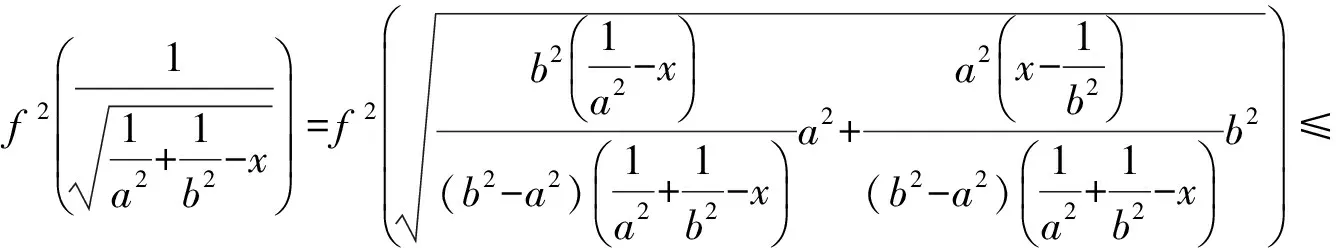
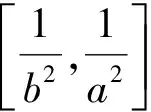
(DepartmentofInformation,PLANavalCommandCollege,Nanjing211800,China)

