极限求法的探讨

贺电鹏

(郑州工商学院 公共基础课教学部,河南 郑州 451400)

极限求法的探讨

贺电鹏

(郑州工商学院 公共基础课教学部,河南 郑州 451400)

探讨了求数列极限和函数极限的常用方法，如数列极限定义法、单调有界定理、洛必达法则、施笃兹定理、定积分定义、压缩性条件、函数极限的定义、两个重要极限、泰勒展式、利用微分中值定理等.给出求每种极限类型的方法、原理,并在其后进行举例说明.

数列极限；函数极限；洛必达法则；施笃兹定理；压缩性条件；泰勒展式；微分中值定理

0 引言

极限概念是高等数学的基本概念之一,高等数学中很多重要概念都是建立在极限概念的基础上的,它是高等数学教学的基础.求极限是高等数学的基本方法.

然而极限定义抽象繁琐,所以很多时候用极限定义本身很难解决所有极限问题;但极限及其运算涉及高等数学及数学分析的始终,并且许多重要的概念都涉及极限,所以极限运算是十分复杂但又不得不重点学习的知识.本文根据多年教学体会及相关参考文献,分别将数列极限的求法与函数极限的求法分为基础类、中等类、复杂类三方面进行探讨，并在每类的每种求法后面附以相关例题说明.

1 数列极限的求法

1.1 基础类

基础类数列极限是最简单的一类数列极限，针对此类数列极限可以利用简单的定义及法则进行求解.数列极限求法的基础类包括定义法、四则运算法等.

1.1.1 利用极限定义

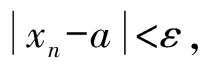
说明用定义法求数列极限有很大的局限性,并不是求极限的好办法,但它是求数列极限的基本方法, 因为在用定义法求数列极限的过程中,可以加深对数列极限概念的理解,并且一些最基本的数列的极限也是依靠它来证明的.求解过程中，首先根据数列的特征,观察出可能的极限值,然后再用定义验证,其关键是找出与ε对应的N(ε).

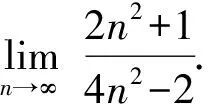
解因为

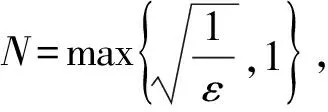
解由于

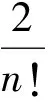
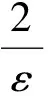
1.1.2 四则运算法则法

定理1[1]若{xn}与{yn}为收敛数列,则{xn+yn},{xn-yn},{xn·yn}也都是收敛数列,且有

特别地，当yn为常数c时有

说明四则运算法则有一定的适用条件，有限个数列加、减、乘、除的数列极限的四则运算法则可以用,对于某些无穷多项的数列,应先应用其他方法,再用四则运算法则求极限.

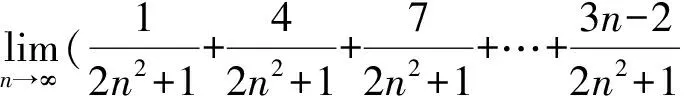
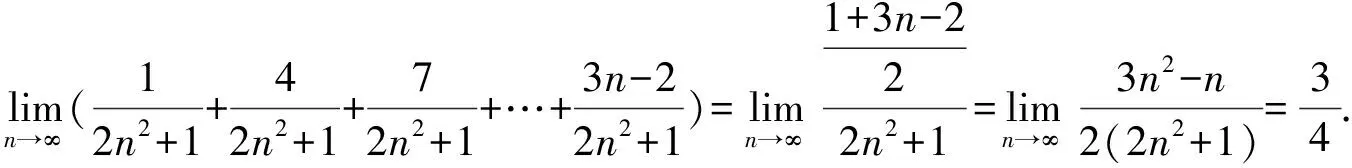
1.2 中等类

中等类数列极限是介于基础类与复杂类之间的一类数列极限，当然也没有明确地划分.此类数列极限可以利用相关的定理及公式进行求解.笔者认为数列极限求法的中等类包括利用单调有界定理、两边夹定理、两个重要极限求极限等.

1.2.1 利用单调有界定理

定理2(单调有界定理)[1-2]在实数系中,单调有界数列必有极限.

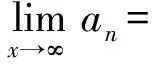
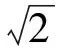
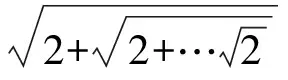
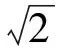
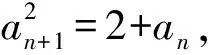
由数列极限的保不等式性知,a=-1是不可能的,所以,

1.2.2 利用两边夹定理(迫敛性)

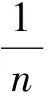
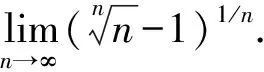
解由

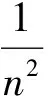
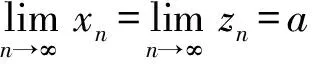
1.2.3 利用两个重要极限

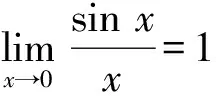
利用两个重要极限是求极限的一个重要手段,要根据题目中给出的条件灵活选择适当的形式,以使运算更加便捷.

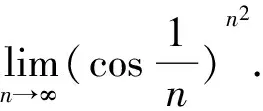
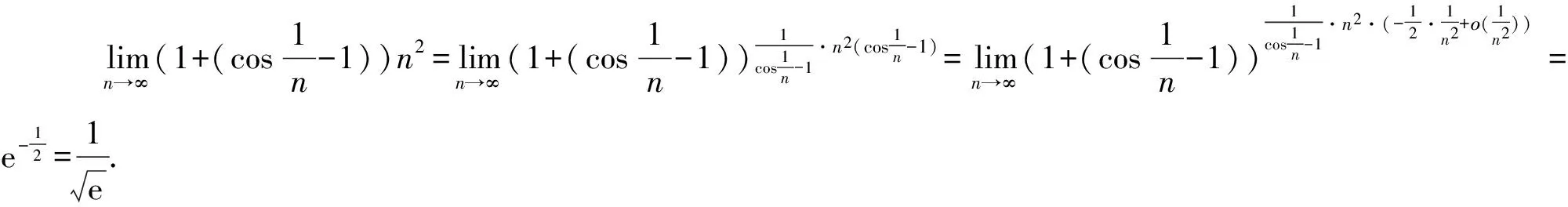
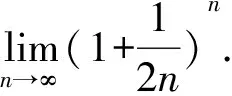
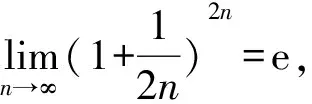
1.3 复杂类

复杂类数列极限是相对比较复杂的一类数列极限，针对此类数列极限可以利用一些定理、定义及公式进行求解.笔者认为数列极限求法的复杂类包括利用施笃兹定理求极限、利用定积分定义求极限、利用压缩性条件求极限等.

1.3.1 利用施笃兹定理

定理4[3-4]设{yn}是单调增加的正无穷大量,

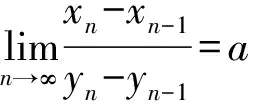
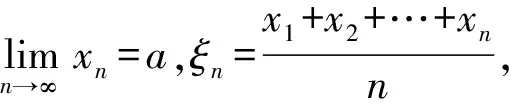
解由施笃兹公式

1.3.2 利用定积分定义

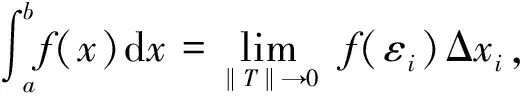
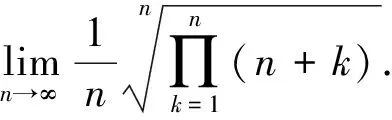
解记

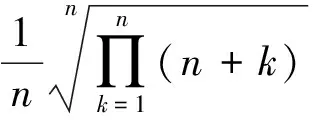
则

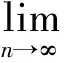
1.3.3 利用压缩性条件

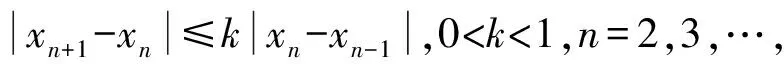
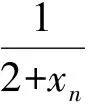
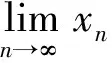
2 函数极限

2.1 基础类

基础类函数极限是最简单的一类函数极限，可以利用简单的定义及法则等进行求解.函数极限求法的基础类包括利用函数极限定义求极限、利用函数极限四则运算法则求极限等.

2.1.1 利用函数极限的定义

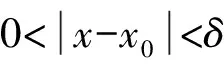
解由于当x≠2时,

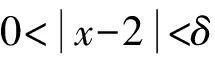
2.1.2 利用极限的四则运算性质

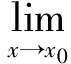
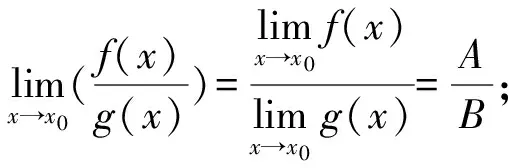
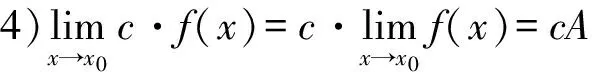
上述性质对于x→∞,x→+∞,x→-∞时也同样成立.

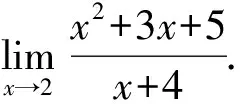
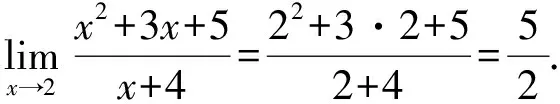
2.1.3 利用通分

对于∞-∞型的函数极限,利用通分将使分母没意义的项消去,进而求极限.

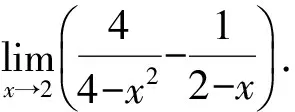
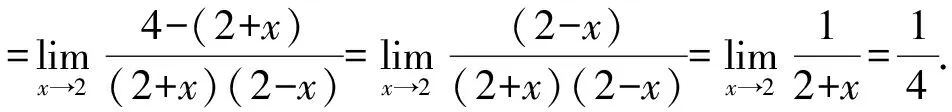
2.2 中等类

中等类函数极限是介于基础类与复杂类之间的一类数列极限，当然并没有明确的划分，可以利用相关的定理及公式进行求解.笔者认为函数极限求法的中等类包括利用无穷小量性质求极限，利用洛必达法则求极限，利用两个重要极限求极限等.

2.2.1 利用无穷小量性质

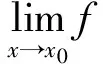
特别是利用无穷小量与有界量之乘积仍为无穷小量的性质.

2.2.2 利用洛必达法则

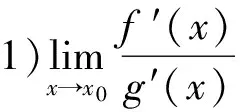
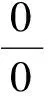
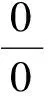
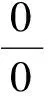
注2洛必达法则并不是万能的,有时使用它比不用它更复杂,不能千篇一律使用,具体题目要具体分析.如以下例17.

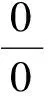
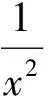
2.2.3 利用等价无穷小代换

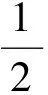
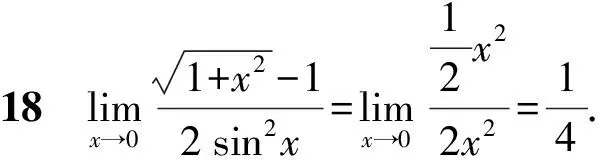
注1在等量代换计算极限时,一般都要强调限定对“乘积因式”的等量代换,对于非乘积因式,有反例表明这样的代换会导致错误的结果,是行不通的.

错解若考虑用“等量代换”由x～sinx,x～tanx将分子部分进行替换,便得出

正解事实上按照极限的运算法则,有

注2很显然,前一种计算方法是错误的.问题就在于当x→0时,sinx-tanx+x3并不是x3的等价无穷小.

2.2.4 利用两个重要极限

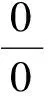
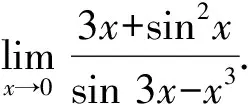
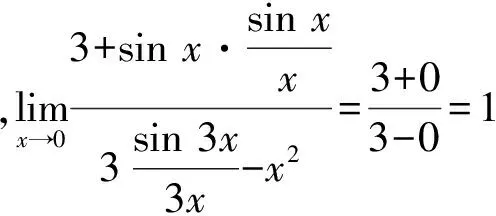
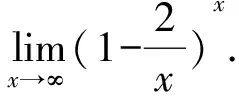
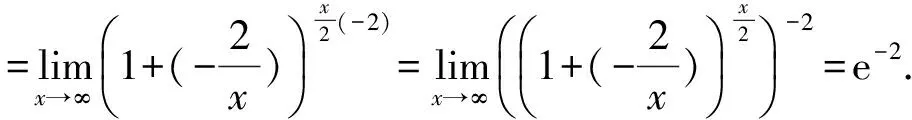
2.3 复杂类

复杂类函数极限是相对比较复杂的一类函数极限，可以利用一些定理及公式进行求解.笔者认为函数极限求法的复杂类包括利用泰勒公式求极限，利用Largange中值定理求极限等.

2.3.1 利用泰勒公式

定理9(泰勒定理)[3,7]若函数f(x)在[a,b]存在直至n阶的连续导函数,在(a,b)内存在(n+1)阶导函数,则对任意给定的x,x0∈[a,b],至少存在一点ξ∈(a,b),使得

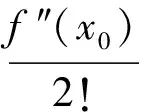
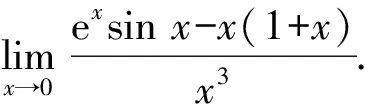
解据题意可知,分母为x3,故分子的泰勒展式不妨取其中的n=3,则

代入不定式中,则有

注1此例用洛必达法则也可以求出.

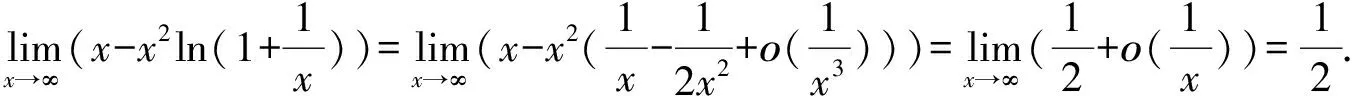
注2此例用前面几种方法很难求出,但是利用泰勒展式就很有效了.

注3考虑泰勒展式求极限时,先求出某个部分在x点的泰勒展式,根据需要取适当的值,并整理,最后求得不定式的极限.

2.3.2 利用Largange中值定理

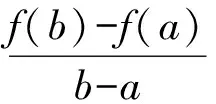
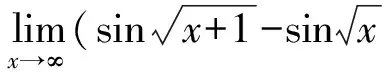
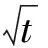
3 小结

求极限的方法应该灵活应用,根据不同的题目选择适当的方法.并在做题的过程中及时总结，力争领悟每种方法的要领，才能更好地掌握求极限的方法，更多地去理解极限求法的重点内涵.求极限的方法还有很多,且有许多方法尚待我们不断努力去研究和探索.

[1] 华东师范大学数学系.数学分析：上册[M].3版.北京：高等教育出版社,2001:24-146.

[2] 同济大学数学教研室.高等数学[M].6版.北京：高等教育出版社,2000:23-70.

[3] 斐礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社,1993:23-76.

[4] 钱吉林.数学分析题解精粹[M].北京：崇文书局，2003:31-102.

[5] 龚思德,刘序球,张广梵.微积分学习指导[M].北京：学苑出版社,1997:36-80.

[6] 周世新.关于函数极限求法的探讨[J].呼伦贝尔学院学报,2009(1):70-72.

[7] 朱永生,刘莉.基于泰勒公式应用的几个问题[J].长春师范学院学报,2006(8):4-25.

[8] 赵普军,孙青茹.例谈求极限的几种不常见方法[J].陕西教育(高教版),2008(4):99-100.

DiscussiononMethodofSolvingLimit

HE Dianpeng
(DepartmentofGeneralEducation,ZhengzhouTechnologyandBusinessUniversity,Zhengzhou451400,China)

Discusses the common method of sequence limit and function limit, including the sequence limit definition, monotone bounded theorem, the Hospital’s Rule, Studz theorem, the definition of definite integral, the compression conditions, the definition of function limit, the two important limits, Taylor expansion, the differential mean value theorem and so on. Give the methods to sovle each kind of limit, and list principles and examples following the methods.

sequence limit; function limit; Hospital’s Rule; Stoltz theorem; compression conditions; Taylor expansion; mean value theorem

2017-03-21

贺电鹏(1988—)，男，河南郑州人，郑州工商学院公共基础课教学部讲师.

10.3969/j.issn.1007-0834.2017.02.011

G642.0;O13

：A

：1007-0834(2017)02-0044-08