典型定积分的计算方法

王 静， 方晓峰， 刘素兵

(火箭军工程大学 理学院,陕西 西安 710025)

典型定积分的计算方法

王 静， 方晓峰， 刘素兵

(火箭军工程大学 理学院,陕西 西安 710025)

牛顿-莱布尼兹公式提供了计算定积分的简便方法，但很多时候原函数不易求出，需要结合其他知识和多种方法求解.介绍了计算定积分的一些方法和技巧，通过举一反三，可增强解决问题的能力.

定积分；变量代换；分部积分；级数

0 引言

定积分是微积分学中的一个重要组成部分，其计算方法除了牛顿-莱布尼兹公式、换元法和分部积分法[1]，还可以充分利用被积函数的奇偶性、周期性、积分区间的对称性等计算定积分[2].但尽管如此，大部分定积分还是很难计算，这里介绍一些典型的计算方法和技巧，以加强计算能力.

1 利用几何图形计算[3]

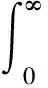
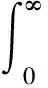
解f(x)=e-x2绕y轴旋转一周的体积为

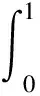
此外，可以视该立体为y=e-(x2+z2)与ZOX平面所围成，如图1所示.于是，体积的另一种表达式为

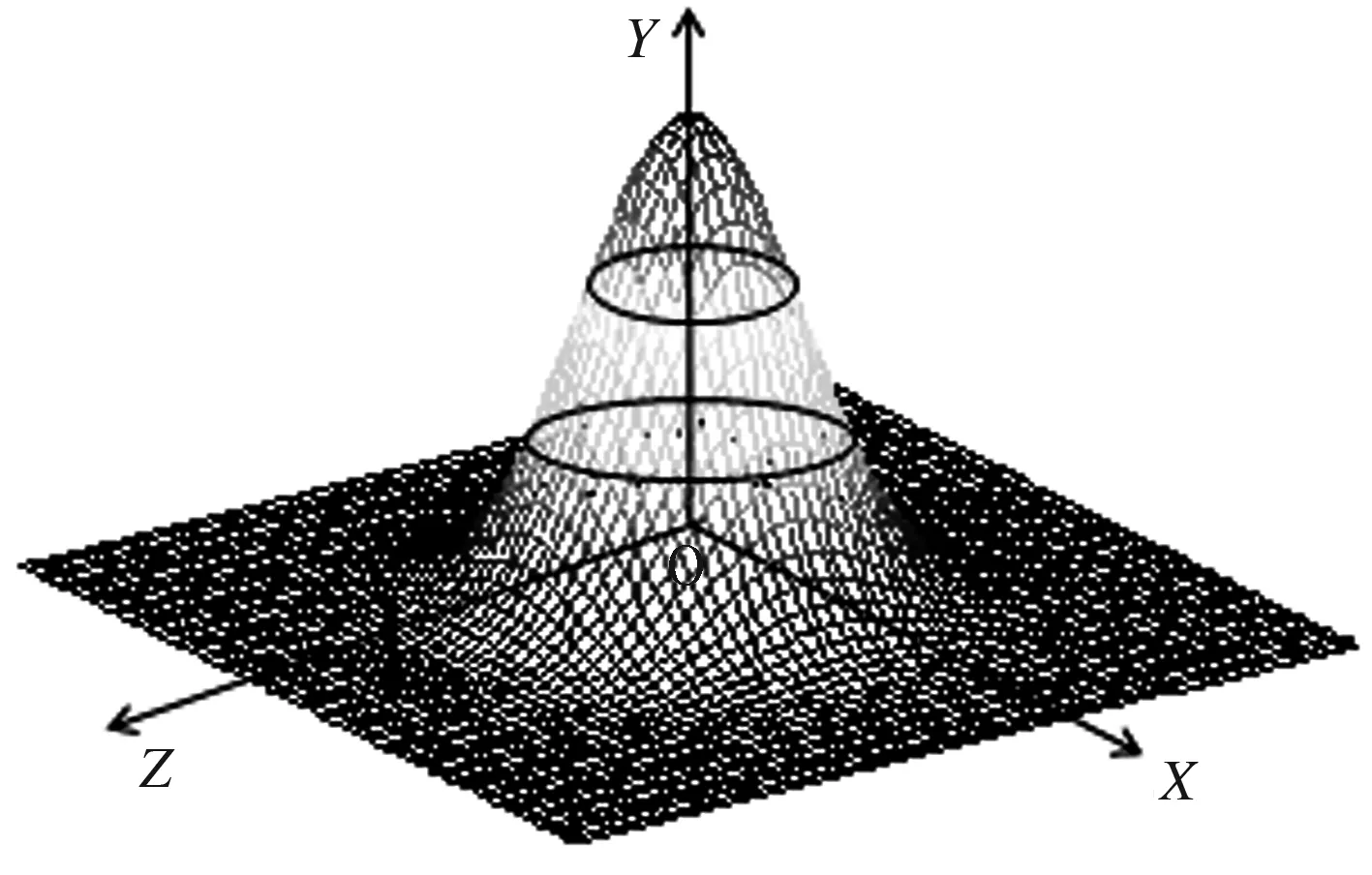
图1 例1图Fig.1 Figure of sample 1

2 巧用分部积分

下面的例子如果用变量代换会很困难.

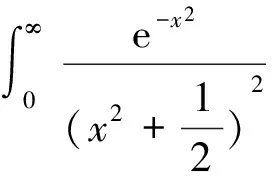
解由分部积分公式可得

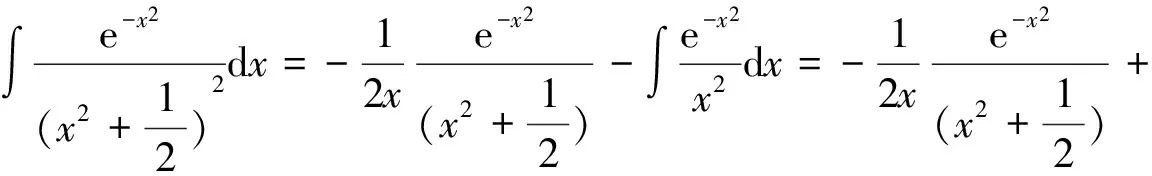
故有

3 根据函数的符号分区间计算

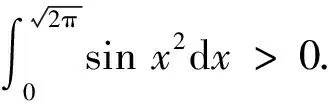
证明对积分作变量代换t=x2，得到

4 利用函数的特性作变量代换

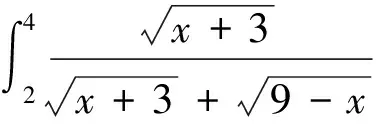
解作变量代换x+3=9-t，那么

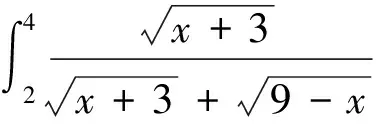
从而

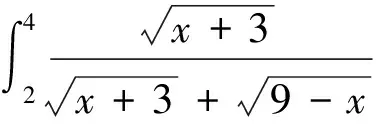
一般地，对于正连续函数f(x)，有

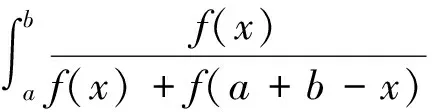
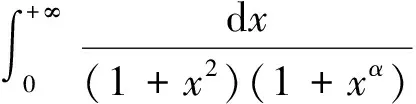
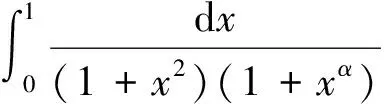
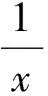
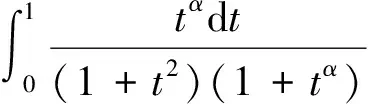
于是

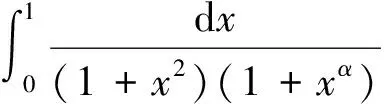
5 几种方法综合使用

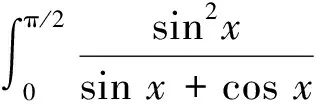
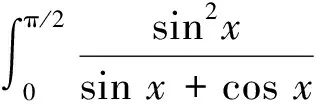
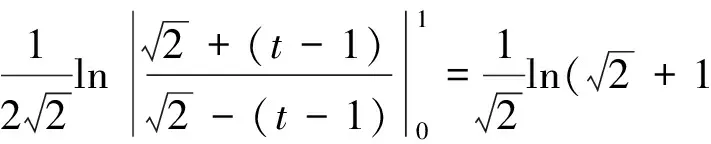
6 经典的方法

对于经典的定积分只有记住其做法.解这类题大多数是绝活，没有别的路好走.

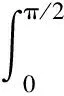
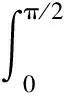
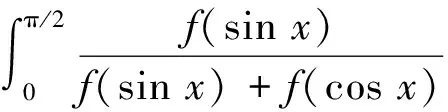
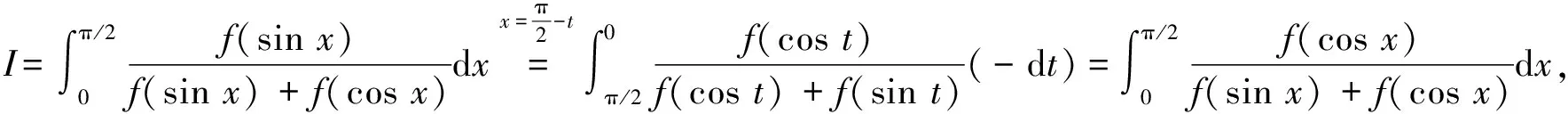
于是

7 利用幂级数的和

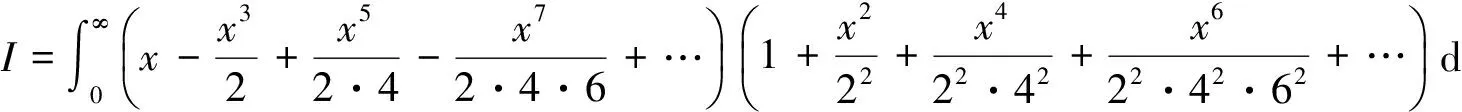
解积分号下第一个级数的和xe-x2/2，由

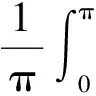
得第二个级数为

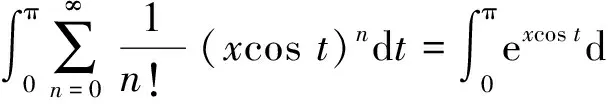
(1)

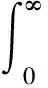
(2)

由于定积分与积分变量无关，故可将式(2)中极坐标形式返回到直角坐标系，仍用x,y表示，得到

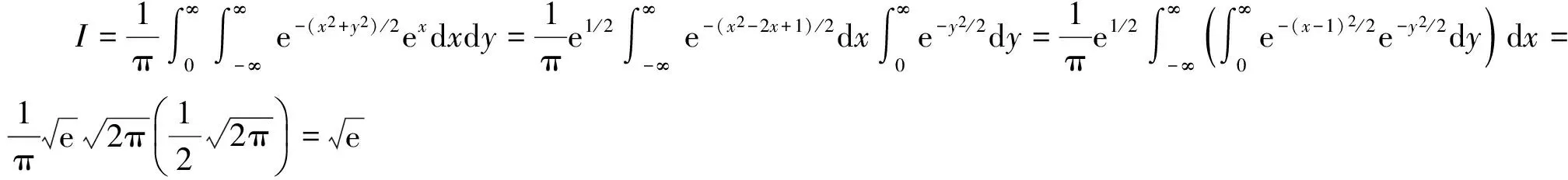
8 利用三角级数的和

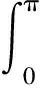
解首先证明

(3)

由

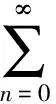
所以(3)式成立.由函数项级数(3)对a2<1时的一致收敛性，故可对级数逐项积分.于是对式(3)两边关于a从0到a逐项积分得到

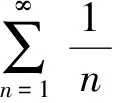
所以

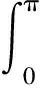
注：该例中m=0时，可以用递推的方法求解.

9 化为已知的积分结果

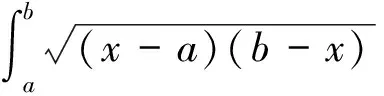
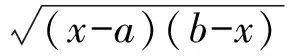
如图2所示.

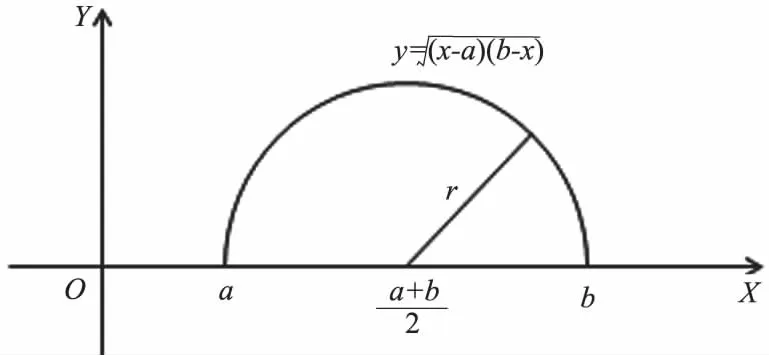
图2 例11图Fig.2 Figure of sample 11

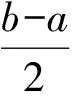
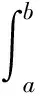
(4)

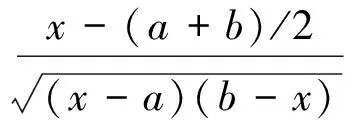
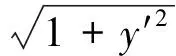
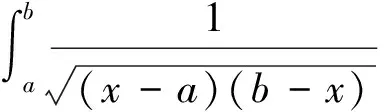
综上所述，本文介绍的计算定积分的方法虽不全面，但是掌握了这些方法，通过举一反三，无疑会大大增强解决问题的能力.

另外，分段函数的定积分需要分段计算，被积函数中带有绝对值或需要开根号时，也要分段处理[5].有些定积分其被积函数的原函数可能求不出来或很复杂，但利用变量代换可化为所求定积分的一个代数方程，便可求得该定积分.如果被积函数本身就是一个变上、下限的定积分，则可通过分部积分的方法化简该定积分，也可利用二重积分交换积分次序的方法计算.

[1] 同济大学数学系.高等数学[M].7版.北京：高等教育出版社，2015.

[2] 刘富.定积分的计算方法[J].山西师范大学学报(自然科学版)，2014(28)：11-14.

[3] 舒阳春.高等数学中若干问题解析[M].北京：科学出版社，2015.

[4] 同济大学数学教研室.高等数学典型题精解——解题思路·方法·技巧[M].北京：学苑出版社，2001.

[5] 屈俊.关于分段函数定积分的计算[J].高等数学研究，2011(14)：63-65.

CalculationMethodofTypicalDefiniteIntegral

WANG Jing， FANG Xiaofeng, LIU Subing
(CollegeofScience,RocketsArmyEngineeringCollege,Xi’an710025,China)

Newton-Leibniz formula provides a simple method to calculate the definite integral, but usually the function is not easy to calculate, it needs to be combined with other knowledge and a variety of methods. Introduces the calculation of the definite integral and some methods and skills, and by inferring the whole from a single instance, the students can strengthen their ability to solve the problem.

definite integral; variable substitution; branch points; series

2017-05-10

高等学校大学数学教学研究与发展中心教学改革项目(CMC20160405)

王 静(1981—), 女, 甘肃武威人，火箭军工程大学理学院副教授, 主要研究方向：代数学环模论和数学教育.

10.3969/j.issn.1007-0834.2017.02.010

O172.2

：A

：1007-0834(2017)02-0040-04