线性方程组的数值解法比较与分析

康玉洁，王亚子，王朝君

（周口师范学院数学与统计学院，河南周口466001）

线性方程组的数值解法比较与分析

康玉洁，王亚子，王朝君

（周口师范学院数学与统计学院，河南周口466001）

讨论求解线性方程组的Gauss直接消元法、Jacobi迭代法和Gauss－Seidel迭代法，并对迭代法的收敛性、收敛速度和误差估计进行比较，对上述两种方法的适用范围及优缺点进行了总结.

直接法；迭代法；Gauss消去法；Jacobi迭代法；Gauss－Seidel迭代

在实际生活中，大部分科学与工程问题最终都要归结为线性方程组的求解问题.目前线性方程组求解的数值方法主要有两类，即直接解法和迭代法.直接法特点是从方程组系数矩阵A和右端常数项b出发，经有限次的代数计算，在不考虑舍入误差的前提下，可获得方程组的精确解.而线性方程组的迭代法也与其他迭代法相似，首先将线性组改写成一种迭代格式，然后再给出初始解向量，经过迭代产生一组解向量的近似值，在收敛时，其序列的极限向量为线性方程组的解.

1 Gauss消去法

直接消去法即指在不考虑舍入误差的前提下，通过有限次迭代运算，可获得方程组的精确解.解线性方程组最常用的方法是Gauss消去法，即逐步消去变元的系数，把方程组化为等价而系数矩阵为三角形的线性方程组，再用回代过程解此等价的方程组.设n元线性代数方程组：

若记A＝（aij）n×n，x＝（x1，x2，…，xn）T，b＝（b1，b2，…，bn）T，则上述n元线性方程组可简记为Ax＝b.

采取顺序Gauss消去法［1－4］，其算法如下：记

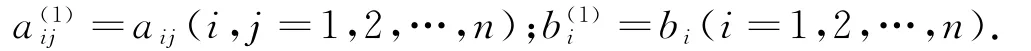
消元过程：对于k＝1，2，…，n－1执行

①若a（k）kk＝0，则算法失效，停止计算；否则转②

②对于i＝k＋1，k＋2，…，n计算

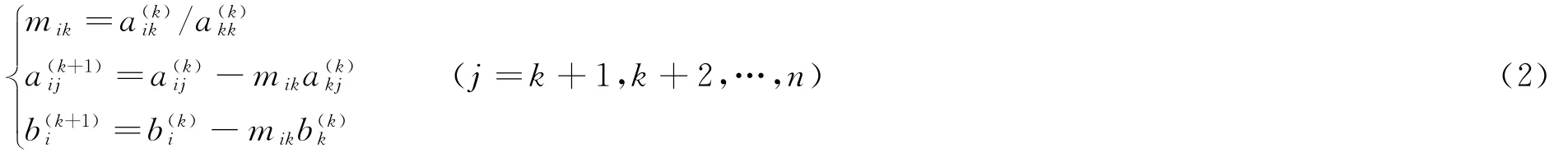
回代过程：

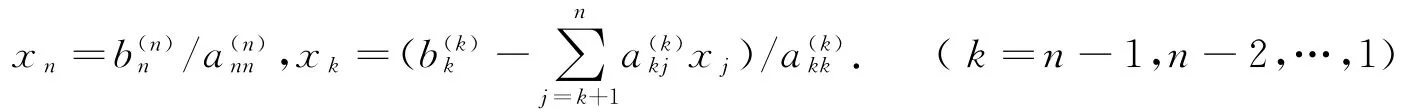
由上述算法可统计出顺序Gauss消元法求解n元线性方程组的乘除法运算总次数为n）.消元的过程与回代的过程一起组成了解线性方程组Gauss消去法的整个过程.

由于三角方程组简单易于求解，所以考虑当系数矩阵A的各阶顺序主子式均不为零时，对系数矩阵采用Doolittle分解［2－6］，即A＝LU，其中L为下三角单位矩阵，U为上三角矩阵，且分解结果唯一.

令

这时，方程组（1）就可以化为两个容易求解的三角形方程组

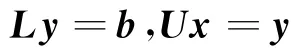
先由Ly＝b解出向量y，再由Ux＝y解出向量x，这就是原方程组（1）的解向量.有分解式（3）以及矩阵相乘法，可知

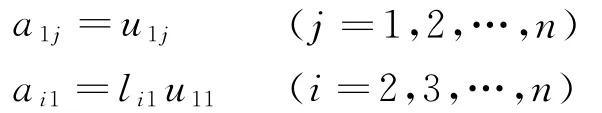
当k＝2，3，…，n时，有

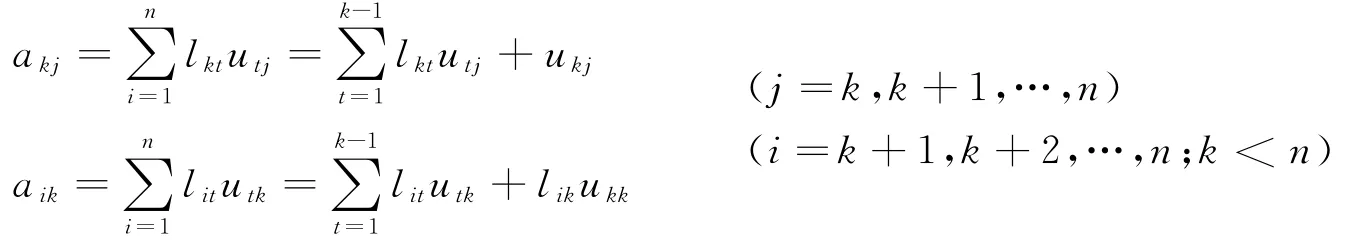
由上述各式得到矩阵A＝（aij）n×n的Doolittle分解计算公式：对于k＝1，2，…，n计算

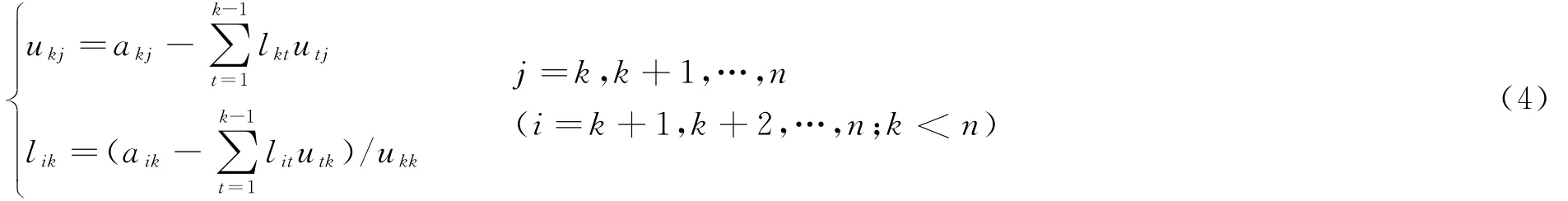
在计算机上计算时，可把ukj和lik的数值分别存放在原akj和aik的存放单元内.分解计算完后，原矩阵A就成为，求解下三角方程组Ly＝b和上三角方程组Ux＝y的计算公式为

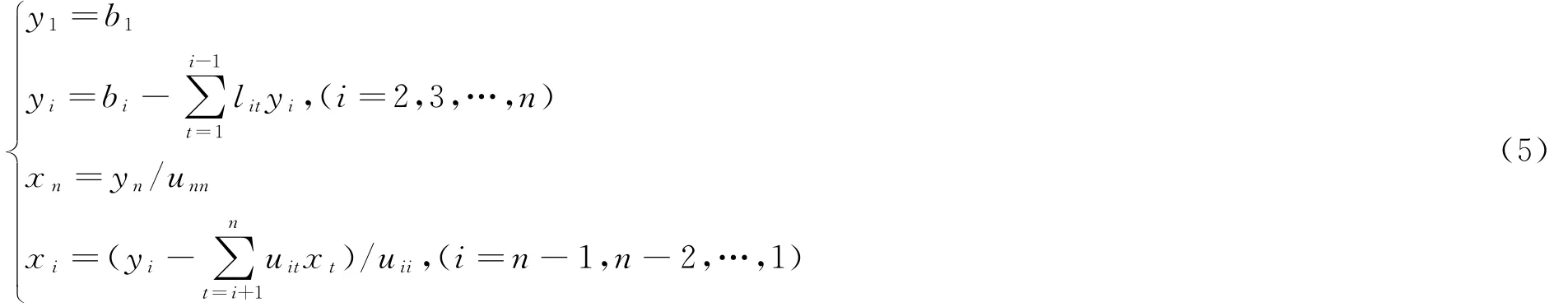
由（4）、（5）两式，就可求解方程组（1）的解向量.

例1 用Doolittle分解求解方程组

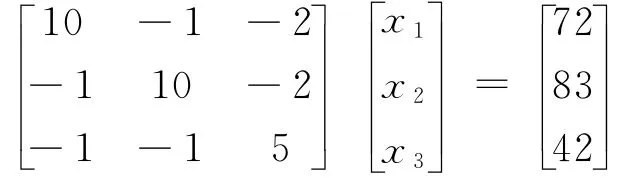
解 运用（4）、（5）两式，可编写程序对问题采取Doolittle分解进行求解，

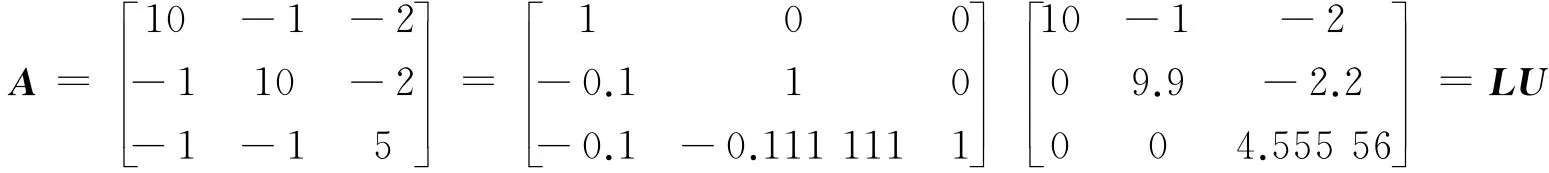
由Ly＝b和Ux＝y可分别解得：y＝（72，90.2，59.222 2）T，x＝（11，12，13）T

此时x＝（11，12，13）T为方程组的精确解.

2 Jacobi迭代和Gauss－Seidel迭代

所谓迭代法，就是根据所给的线性方程组设计一个迭代公式，由迭代公式构造一个向量序列.若此向量序列收敛，则它的收敛极限就是相应的线性方程组的解.其中Jacobi迭代法［3－4，7－10］是基本的迭代方法，下面就考虑其具体的迭代过程和收敛性.

2.1 Jacobi迭代

对非奇异线性代数方程组Ax＝b，设系数矩阵A＝（aij）n×n∈Rn×n满足条件aii≠0（i＝1，2，…，n），令

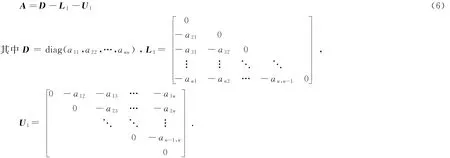
由已知条件，D－1存在，那么（1）可以写成

其中B＝D－1（L1＋U1），g＝D－1b.

若任意给定初始向量x0＝（x（0）1x（0）2…x（0）n）T，并代入（7）右端，就可以计算出一个新的向量x1，即x1＝Bx0＋g；再把x1代入（7）右端，又得到一个向量x2；依次类推有xk＝Bxk－1＋g，（k＝1，2，3，…），其分量形式是

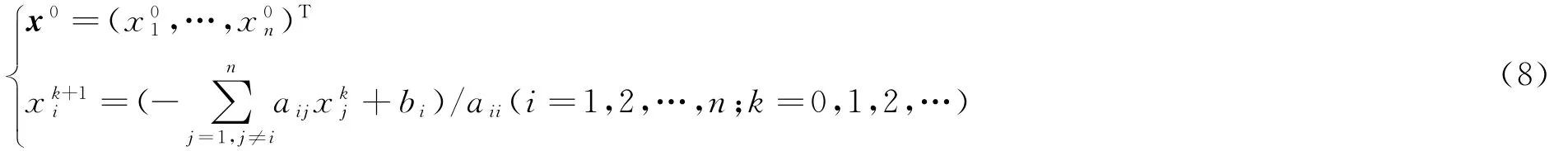
2.2 Gauss－Seidel迭代

在Jacobi迭代公式（8）的使用过程中，要同时保留两个近似解向量xk和xk＋1.如果把迭代公式改成

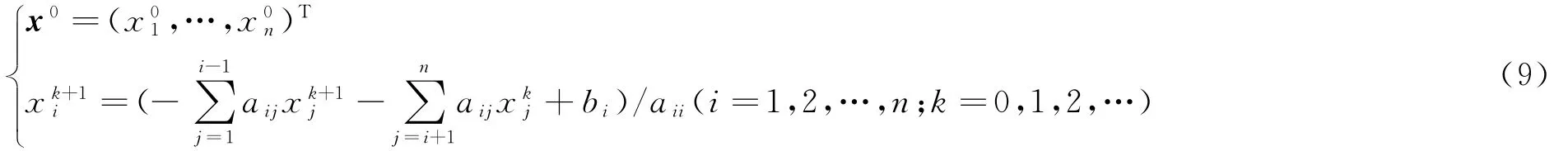
其中M＝（D－L1）－1U1，g＝（D－L1）－1b.

这样，在整个计算过程中，只需用n个单元存贮近似解的分量.而且通常认为，新近似解可能比老近似解更接近精确解，因此，可望这样迭代会更有效.

选取初始向量x0，用迭代公式（9）产生近似解序列xk｛｝，这种方法叫Gauss－Seidel迭代法，式（9）为Gauss－Seidel迭代法的运算公式.

2.3 Jacobi迭代和Gauss－Seidel迭代的收敛性

通过Jacobi迭代和Gauss－Seidel迭代的过程可以看出新得出的近似解xk＋1与已知近似解之间存在着线性关系，而且仅与xk有关，即可表示成如下形式

其中，对Jacobi迭代：M＝D－1（L1＋U1），g＝D－1b；对Gauss－Seidel迭代：M＝（D－L1）－1U1，g＝（D－L1）－1b.

定理1［3－4］解方程组（1）的单步线性迭代（11）收敛的充要条件是M的谱半径ρ（M）＜1.

定理2［3－4］若迭代矩阵M的范数‖M‖＝q＜1，并假定范数‖I‖＝1，则线性迭代法（11）的第k次近似和准确解x＊之差有估计式：

从近似解的误差估计式（12），根据事先给定的精度ε，可以计算要得到满足精度要求的近似解需要迭代的次数k：

例2 用Jacobi迭代求解例1，并且要求各个分量的误差绝对值不超过10－4.

则

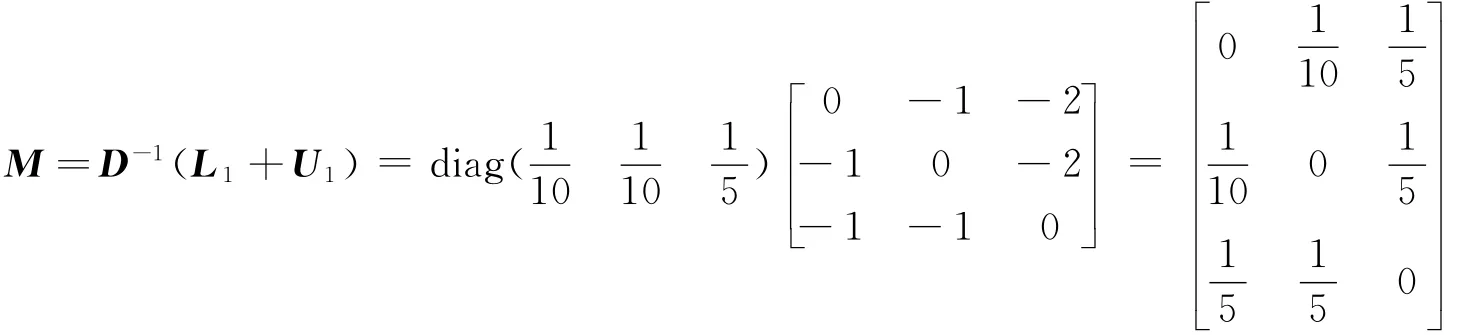
再用Jacobi迭代法求解线性方程组.由Jacobi迭代法的计算公式（8），有

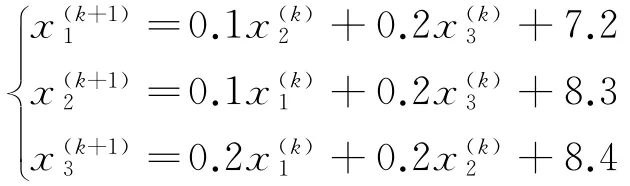
取x（0）＝（0，0，0）T，代人上式，得：

如此继续下去，运用程序，迭代结果见表1.

在Jacobi迭代法收敛的情况下，迭代9次，得近似解x（9）＝（10.999 4，11.999 4，12.999 2）T，由例1可得方程组的精确解为x＊＝（11，12，13）T，从表1可以看出，当迭代次数增加时，迭代结果逐步接近精确解.

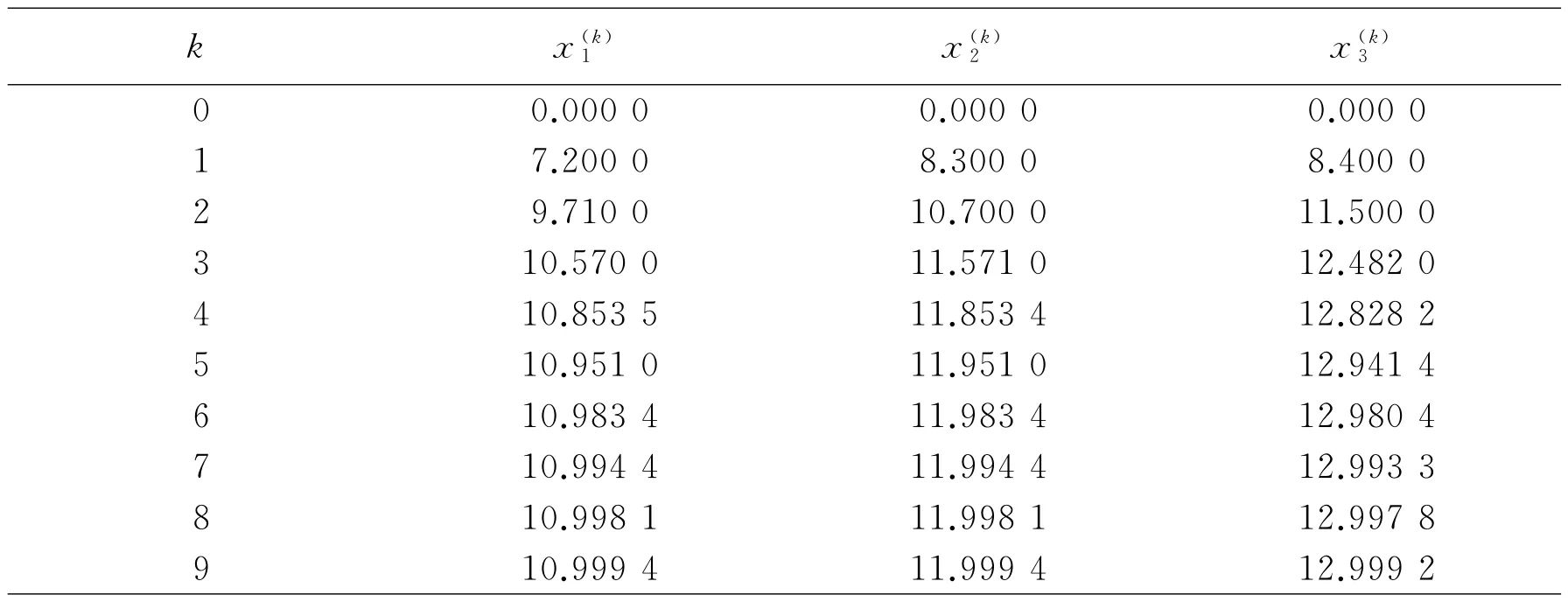
表1 Jacobi迭代所得解

近似解要求各分量的误差绝对值不超过10－4.若对上述方程组的近似解要求各分量的误差绝对值不超过10－4，则由

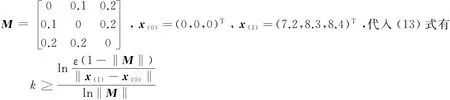
例3 用Gauss－Seidel迭代求解例1.

解 先判断Gauss－Seidel迭代法的收敛性

M的谱半径为ρ（M）＝0.073＜1，所以Gaus－Seidel迭代法收敛.

再用Gaus－Seidel迭代法求解线性方程组.由Gaus－Seidel迭代法的计算公式，有

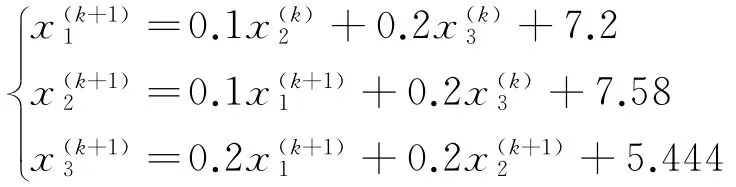
取x（0）＝（0，0，0）T，代人上式，得：如此继续下去，运用程序，迭代结果见表2.

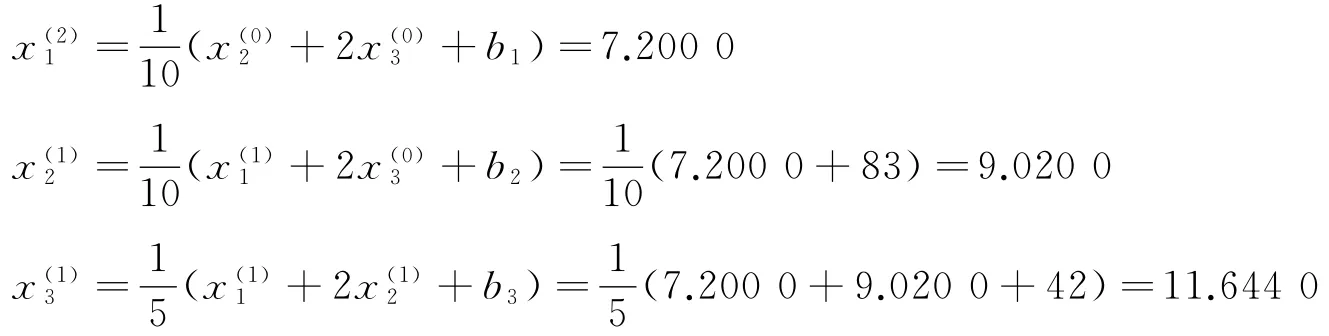
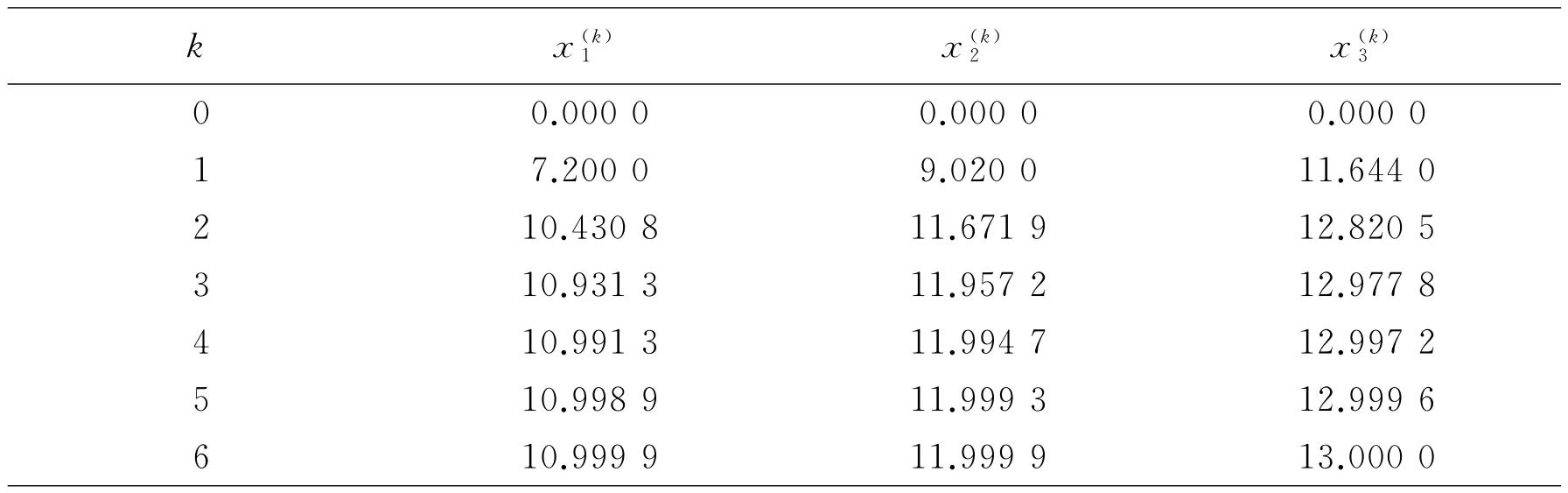
表2 Gaus－Seidel迭代所得解

2.4 高阶稀疏矩阵应用迭代法求解

对于高阶线性方程组，尤其是高阶稀疏矩阵应用迭代法求解一般有下面几个步骤：

（1）构造迭代序列；

（2）构造的迭代序列的收敛性；

（3）如果收敛，收敛的速度.在解题时应给出量的刻画，用以比较各种迭代方法收敛的快慢；

（4）在有限次计算过程中，要考虑和估计近似解的误差，以及处理迭代过程产生的中断等问题，这就需要分析舍入误差［5，10－12］.

根据题中所给系数矩阵，首先判断该迭代方法是否收敛；如果收敛，再根据求解所要求达到的精度，可以设计算法计算出要迭代的次数，采用Jacobi迭代、Gauss－Seidel迭代或其他迭代方法，经过有限步迭代，可求解出较为精确的近似解.

由以上对Jacobi迭代法和Gauss－Seidel迭代法的论述知，当向量序列收敛时，其极限就是方程组的解.当方程组的系数矩阵为高阶稀疏矩阵时，运用Jacobi迭代法即可以维持系数矩阵的稀疏特性，又容易计算和编写计算机程序，并且在很多问题中，具有较快的收敛速度，适用于大型线性方程组，尤其是稀疏线性方程的求解问题.Gauss－Seidel迭代法对Jacobi迭代法进行改进，在Jacobi迭代公式的使用过程中，要同时保留两个近似解向量xk和xk＋1.对于Gauss－Seidel迭代法每算出新近似解，在算下一个近似解时，用新近似解代替老近似解进行计算.这样，在整个计算过程中，只需用n个单元存储近似解的分量.而且通常认为，新近似解可能比老近似解更靠近精确解，因此，可望这样迭代会更有效.

3 结束语

在计算机存储量允许的情况下，直接法是求解中小型线性方程组的有效方法，其中Gauss直接消元法作为最基本的一种直接法，其运算量为.由此可见，对于中小规模线性方程组（即方程组的阶数不高，比如小于1 000），它具有运算量小，效率高等优点，但该方法用于高阶方程组时计算量太大而不实用.它一般用于线性方程组的系数矩阵稠密（即系数矩阵中，大部分数据均非零），且又没有任何特殊结构的线性方程组.

现今，随着运算技术的飞速发展，电子计算机的贮存量逐渐加大，所需计算时间急速减少.在计算机上，对于高阶的线性方程组，可运用直接法（如Gauss消去法）来进行求解，但是直接法往往需要对系数矩阵A进行Doolittle分解，因而大多数情况下丢失了系数矩阵A的稀疏性.但是在现实生活中，特别是求解偏微分方程的数值解时，常遇到的恰恰就是大型稀疏线性方程的求解问题.

对于高阶线性方程组，如果运用直接消元法进行求解，运算量过大，故采用迭代法.迭代法具有存储空间小，程序简单的优点，所以对于大型的线性方程组，迭代法更有优越性.线性方程组的迭代解法与直接消元法不同，其精确解不能经过有限次的计算而获得，而是通过迭代逐步逼近它.因此，凡是迭代解法都有一个收敛性问题，不收敛的方法是不能使用的.但迭代解法具有稀疏的系数矩阵，所需存储空间少，而且程序设计简单，适用于自主计算，用较少的运算量，就可以得到较合理的结果.因此，对于线性方程组，特别是系数矩阵是大型稀疏的线性方程组来说，一种非常重要方法就是运用迭代法求解.

Jacobi迭代法和Gauss－Seidel迭代法是两种最基本、最简单的方法，其中Jacobi迭代法具有很好的并行性，而Gauss－Seidel迭代法是典型的串行算法.对于同一个线性方程组，这两种方法可能同时收敛，也可能同时发散，也可能其一收敛，而另一发散.但当两者皆收敛时，一般来说Gauss－Seidel迭代法比Jacobi迭代法收敛的快.

［1］刘长安.数值分析教程［M］.西安：西北工业大学出版社，2005：98－101.

［2］颜庆津.数值分析［M］.北京：北京航空航天大学出版社，2006：73－75.

［3］徐树方，高立，张平文.数值线性代数［M］.北京：北京大学出版社，2004：104－105.

［4］A D Gunawardena，S K Jain，L Snyder.Modified iterative methods for consistentlin earsy stems［M］.1991：123－143.

［5］曹志浩.数值线性代数［M］.上海：复旦大学出版社，1996：125－127.

［6］丁丽娟，程杞元.数值计算方法（2版）［M］.北京：北京理工大学出版社，2005：63－65.

［7］冯有前，王国正，李炳杰，等.数值分析［M］.北京：清华大学出版社，北京交通大学出版社，2006：47－49.

［8］张耀仁.C＋＋程序设计［M］.北京：中国铁道出版社，2006：285－294.

［9］薛秋芳.解线性方程组的几种迭代法的收敛性分析［D］.西安：陕西师范大学，2005.

［10］S P Han.A lobally convergent method for nonlinear programming［J］.Journal of Optimization Theory and Applications，1977（22）：297－309.

［11］J V Burke，S P Han.A robust sequential quadratic programming method［J］.Mathematical Programming，1989（43）：277－303.

［12］M Delfour，M Fortin，G Payre.Finrte Difference Solution of a Non－linear Schrodinger［J］，Equation.J.Comput.Phys.，1981（3）：277－288.

Comparison and analysis of numerical methods for solving linear equations

KANG Yujie，WANG Yazi，WANG Chaojun
（School of Mathematics and Statistics，Zhoukou Normal University，Zhoukou 466001，China）

This paper researches the method for the linear algebra equations：the direct Gauss elimination method，the Jacobi iterative method and the Gauss－Seidel iterative method，compare the astringency，the convergent rate and the error estimation，then analyze the scope of application and the advantage and disadvantage of the two methods.

direct method；iterative method；Gauss elimination method；Jacobi iterative method；Gauss－Seidel iterative method

O241.6

A

1671-9476（2017）02-0036-07

10.13450／j.cnkij.zknu.2017.02.009

2016-08-09；

2016-12-22

河南省科技厅科技发展计划项目（No.162102310619）；河南省高等学校重点科研项目（No.17A110038）；周口师范学院教育教学改革研究项目（No.J2016006）

康玉洁（1986－），女，河南周口人，助教，硕士，主要从事不确定理论研究.