水陆两栖车摇臂式收放轮机构设计

孙荣哲

(大连浦州航空科技有限公司)

水陆两栖车摇臂式收放轮机构设计

孙荣哲

(大连浦州航空科技有限公司)

针对某型水陆两栖车收放轮要求，设计了一种结构简单，重量轻，性能可靠的收放轮机构，并根据该机构的力学特点进行了主要零件受力分析以及电机需用扭矩计算。

水路两栖车收放轮机构 电机需用扭矩 自锁

0 前言

水上航行速度是水陆两栖车的一项重要指标。相对于船艇，两栖车结构复杂，重量大吃水深；流线形车身被车轮以及车轮悬架破坏；造成航行阻力大。所以多数两栖车采用收放轮结构，在水中行驶时将车轮收起于水面之上，减小阻力。达到提高车速的目的。而收放轮装置设计的优劣直接影响陆地行驶性能以及水中航行阻力的大小。

目前比较成熟的两栖车产品有英国吉布斯公司的Humingda、Gibbs Humdinga和Gibbs Quadski，瑞士Rinspeed公司的Splash，美国watercar公司的两栖车，这些两栖车最高航行速度都可以达到70～80km/h。国内对两栖车的研制起步较晚，与国外相比有较大差距。收轮机构不成熟，水上航行速度一般不超过20km/h。水上航行速度低的一个重要原因是水中阻力过大，如果能够实现车轮收起至水面以上且对船体流线形体破坏较少，将会显著提高两栖车性能。

本文设计了一种外挂式轮边驱动系统的收放轮机构，其机构如图1、图2所示。

此收放轮机构的轮边完全悬挂在两栖车车体外侧，保持了车体底部的流线型低阻外形。当收放轮时，电机经减速箱驱动摇臂拉起减震器，减震器拉动传动臂使其绕着A点转动。摇臂旋转一周的过程中，在车轮下止点与上止点位置摇臂与减震器相互平行，此时减震器传给摇臂的力完全平行于摇臂，因此不会对摇臂产生扭矩，摇臂只受到拉力或压力。

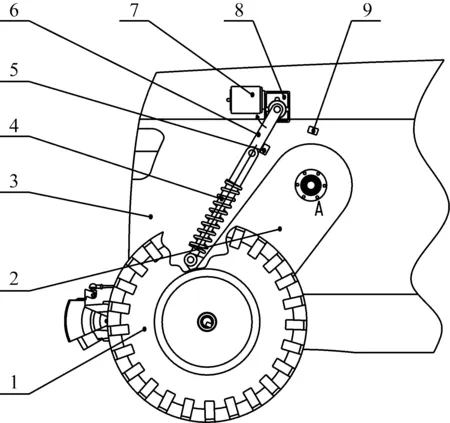
1.车轮；2.传动臂；3.车体；4.减震器；5.下限位块；6.摇臂；7.电机；8减速箱；9.上限位块

图1 收放轮机构简图(放下状态)

Fig.1 Wheel suspension folding mechanism(drop state)

本结构的力学简化模型如图3所示，传动臂、减震器、摇臂构成了一个曲柄摇杆机构。摇臂旋转一周，传动臂上下摇摆一次，摇摆过程中摇臂有两次与减震器相平行，形成死点。

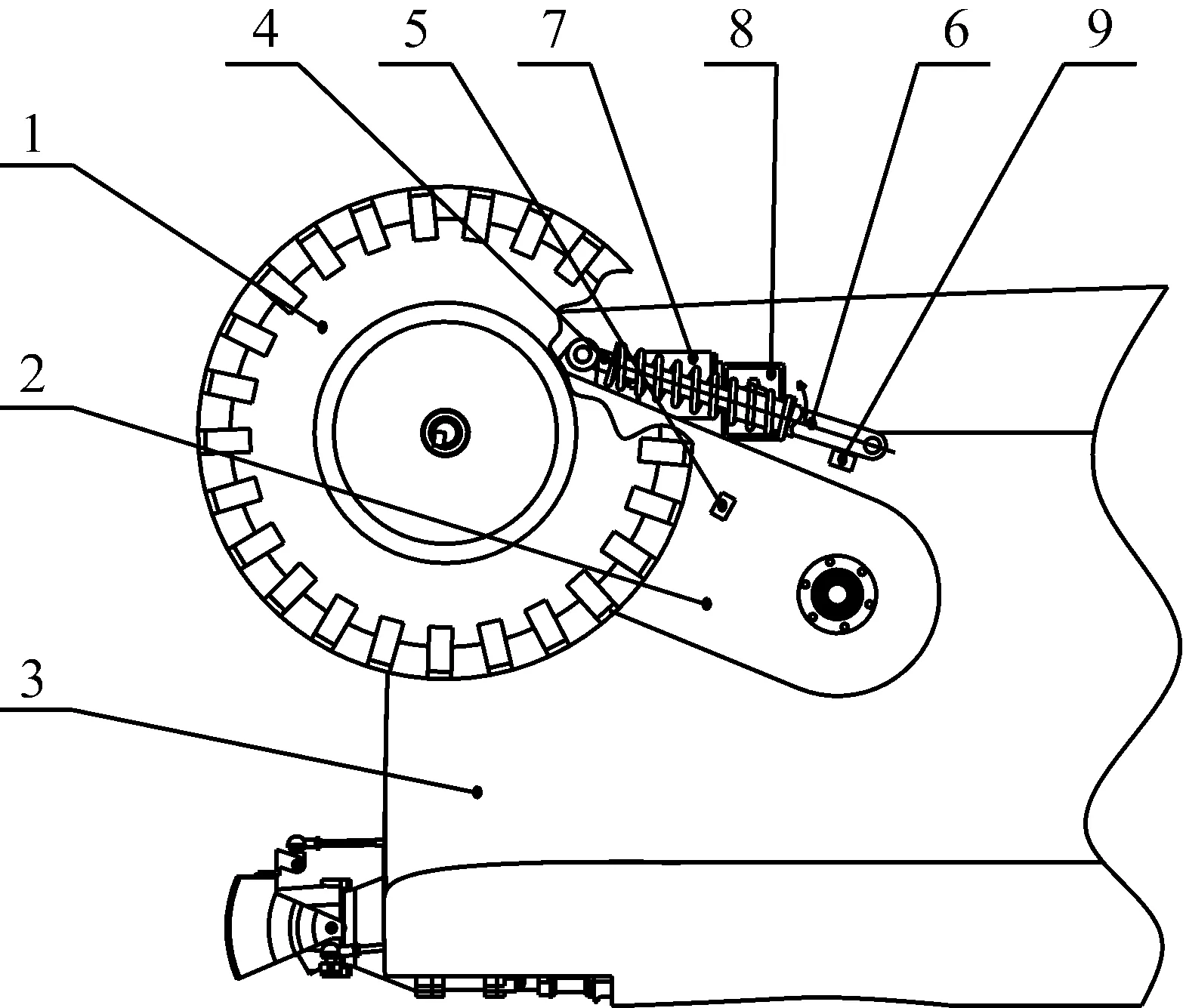
图2 收放轮机构简图(收起状态)

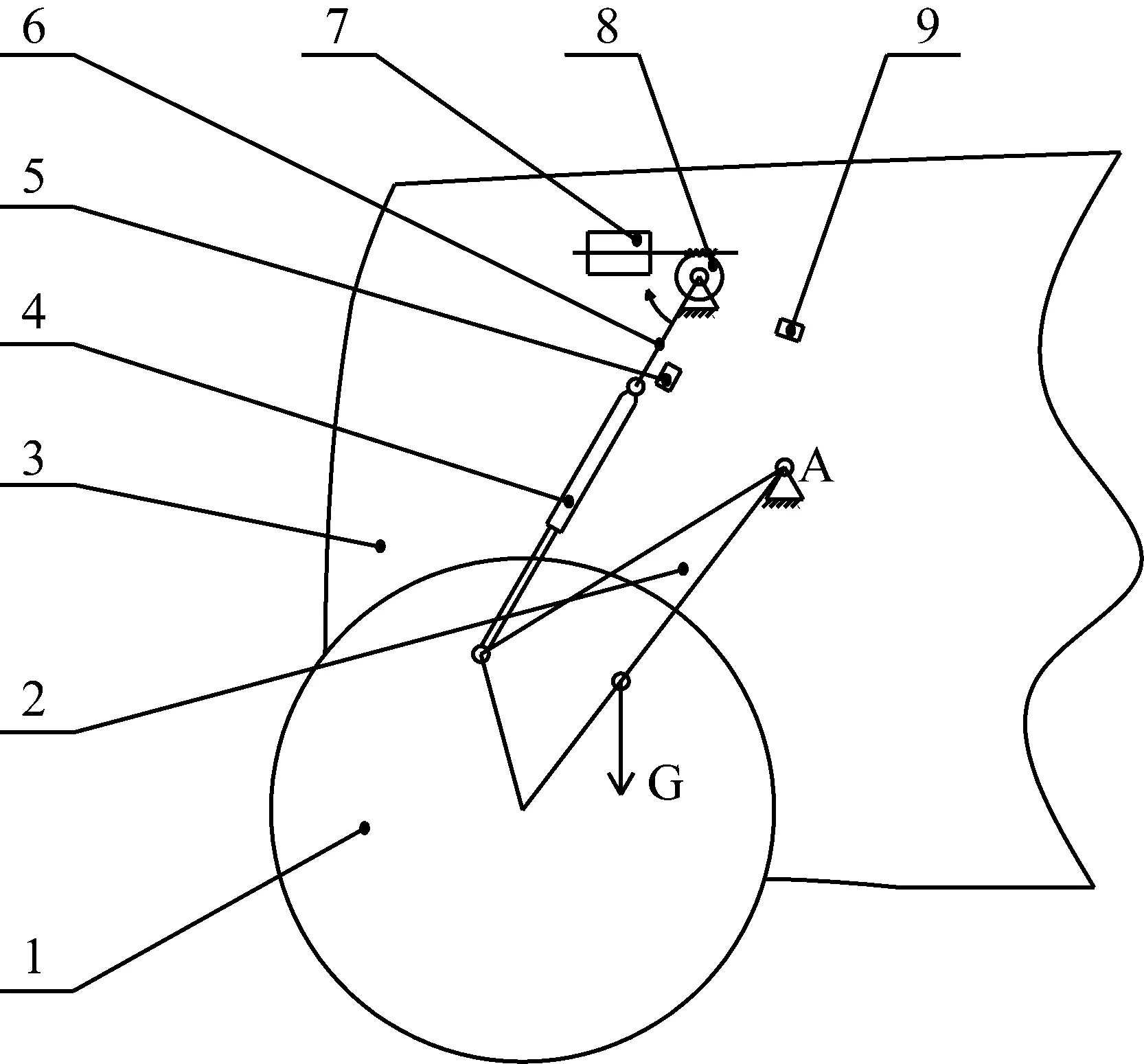
图3 力学简化模型

1 指标要求

根据该两栖车设计要求，收放轮机构要求如下：

2 机构受力分析

车轮收起过程中，机构中杆系受力情况如图4所示；件2传动臂上扭矩平衡，可得方程式：

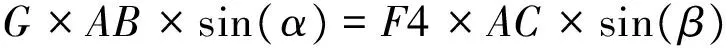
(1)

件4减震器为二力杆，所以件4施加给件6摇臂的力矩为：

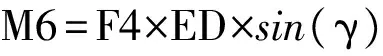
(2)

将(1)式带入@2)式可得

(3)

由(3)式可以看出，欲求电机需用扭矩必须求得γ、α、和β的角度，其余摇臂长度、传动臂等尺寸参数均为已知的设计值。在摇臂旋转一周的过程中G、AB、ED、AC值均保持不变，而γ、α、和β角均随着摇臂的转动而变化。以A点为原点建立坐标系如图4所示。图中，确定各角度值的关键在于确定D点、C点的位置，由于已知摇臂长度和摇臂初始角度与旋转角度，其中D点的位置可以很容易求得。而C点位置不容易求得，从几何关系上分析，它是两个圆的交点，一个圆是以D点为圆心，CD为半径的圆，另一个圆是以A点为圆心，AC为半径的圆。因此可得两个方程：

(4)

(5)

注：XC、YC为C点横纵坐标；XD、YD为D点横纵坐标。

此二元二次方程求解比较复杂且不是本论文重点，借助数学工具以摇臂旋转角度为变量计算D点位置，再以D点位置计算C点位置，迭代摇臂旋转角度得到摇臂旋转一周C点、D点轨迹如图5所示。图中D点绕E点旋转一周，减震器CD保持长度不变，拉动C点绕坐标原点A沿弧线轨迹运动一个反复。

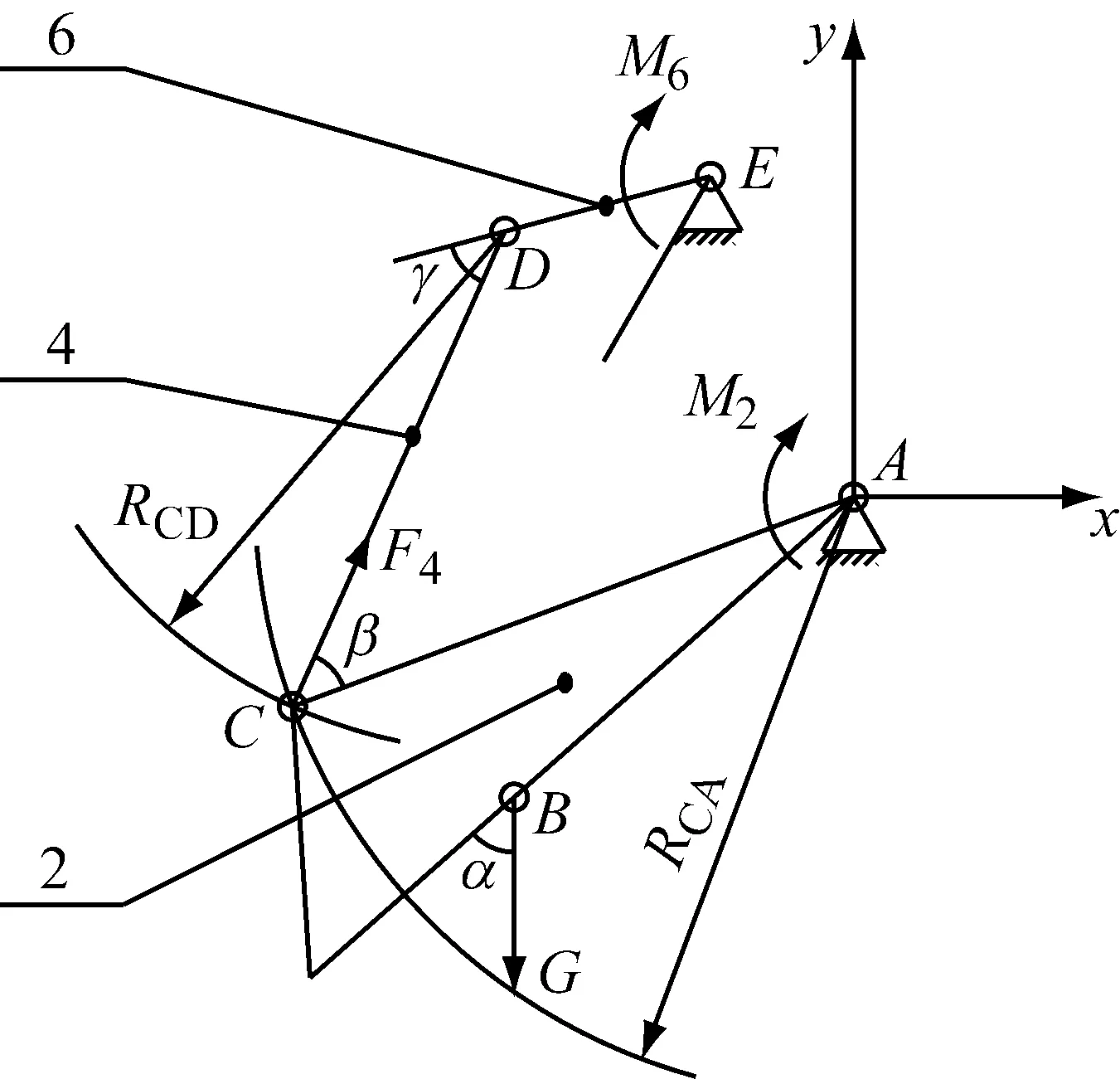
图4 杆系受力分析

根据C、D点坐标计算各杆角度以及杆系间夹角，其变化曲线如图6所示。图6中，以摇臂旋转角度为横轴，对应链盒角度α、链盒间夹角β、减振器与摇臂间夹角γ的角度为纵轴，绘制出α、β、γ的变化曲线。随着摇臂旋转角度的增加，链盒角度α由初始37°逐渐增大，当摇臂旋转258°时，α增加至最大值112.4°，此时车轮被收起至最高点，然后随着摇臂旋转角度的增加，再降回37°。减振器与链盒间夹角β由28°开始，在11°～60°之间波动，最终回到28°。减振器与摇臂间夹角γ由0°开始逐渐增大，在摇臂旋转258°时达到180°，此时摇臂与减振器折叠重合。摇臂继续旋转至360°时，γ角也旋转至360°回到初始位置，机构处于同样的图2位置，摇臂与减振器轴线重合。γ角为0°或180°时摇臂与减振器处于折叠重合或轴线重合，减震器对摇臂拉力产生的扭矩为F4×ED×sin(γ)，因sin0°或sin180°的值都为零，所以摇臂所受扭矩为0。

图5 C、D点运动轨迹

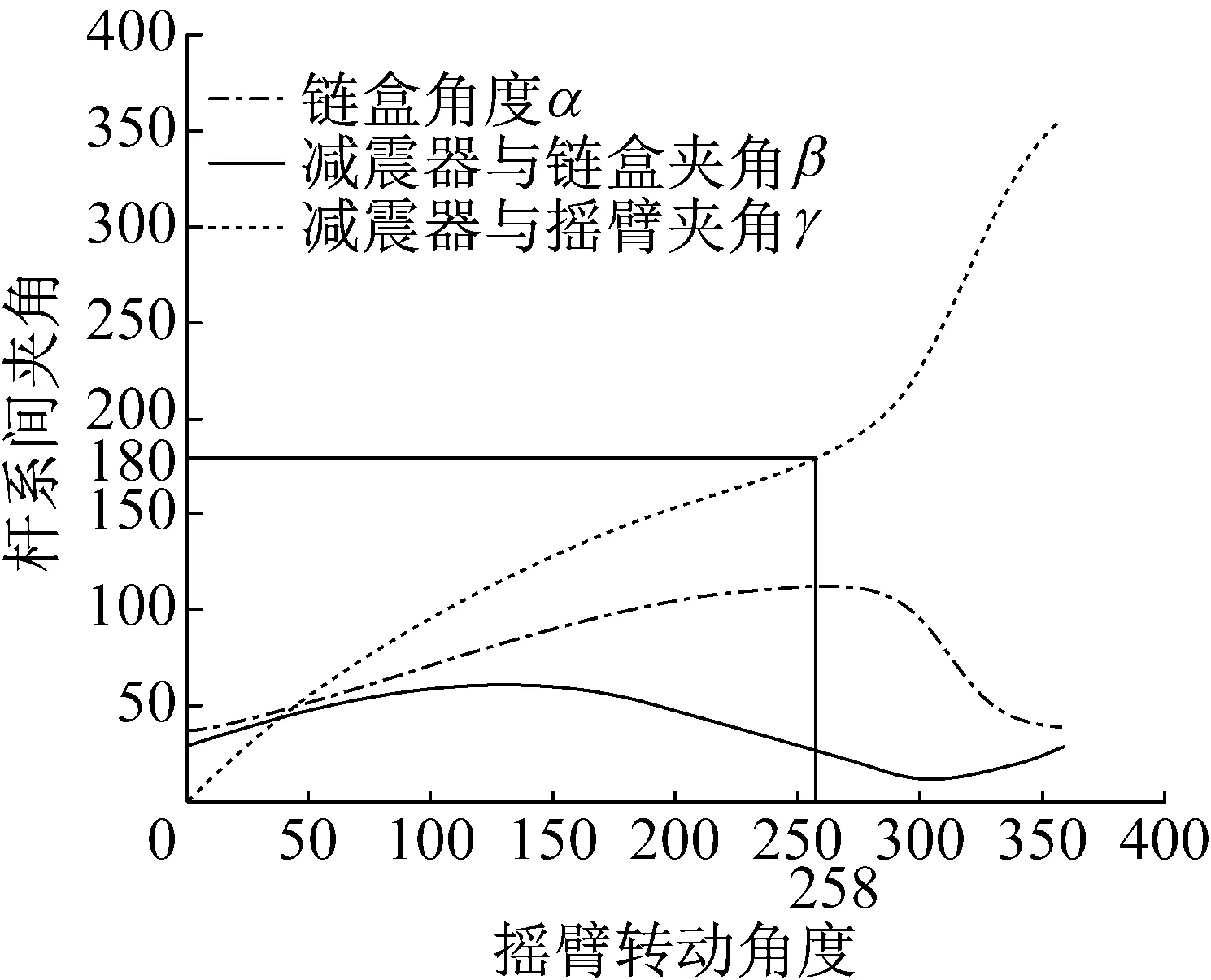
图6 杆系夹角变化曲线

摇臂需用扭矩如图7所示。图7中，摇臂由图2位置(下死点)开始顺时针旋转一周回到初始位置。可以看出，从初始位置至258度区间，摇臂受到逆时针方向扭矩，扭矩由0开始逐渐增大至54N.m(摇臂旋转100°时)。然后再逐渐降低至0(摇臂旋转258°时)，到达上死点。然后摇臂继续顺时针旋转，摇臂受到扭矩变为顺时针方向并迅速升高，最高达到225N.m(摇臂旋转312°时)。然后又迅速降低至0。回到下死点。由图7可以看出，摇臂旋转角度在0～258°区间时，摇臂扭矩变化比较平缓，最大扭矩只有54 N.m，而在后半段摇臂旋转的角度较小，只有102°，但是摇臂扭矩变化剧烈，需要的最大扭矩太大，不利于减小电机功率和结构尺寸，因此选择前半段0°～258°区间为本结构的工作区间，并在区间分隔点设置限位块以防止摇臂旋转过度。

图7 摇臂需用扭矩变化曲线

3 减速机与电机选择

根据需用扭矩为Nmax=54 N.m，选用减速比n为1:50的涡轮蜗杆减速机，查其机械效率η为79%，可计算得到需用电机扭矩为：

Nd=Nmax/n/η=54/50/0.79=1.37 N.m

电机选用额定扭矩2 N.m，扭矩裕度为1.46，电机转速转速900rpm。计算可得摇臂转速为18rpm。旋转258°收放车轮需用时间为2.4秒。

[1] 《基于车轮收放技术的两栖车悬架的运动学特性对比研究》，王重阳，吴志成，吴靖杰，机械设计与研究，2013.

[2] 《水陆两栖车辆减阻增速关键问题研究》，宋桂霞，博士学位论文，南京航空航天大学，2008.

[3] 《基于流体仿真的两栖车车轮收起前后阻力对比分析》，吴珂，宋桂霞，赵又群，系统仿真技术，2007.

[4] 《悬架变动对水陆两栖车辆性能的影响》，宋桂霞，赵又群，吴珂，机械科学与技术，2008.

[5] 《高速两栖车滑行车体阻力分析与可实现形式》，贾小平，邢俊文，于魁龙，车辆与动力技术，2001.

Design of Suspension for the Amphibious vehicle

SunRongzhe

(PANWOOAviationTechnologyCo.,Ltd)

In order to meet the demand of the Suspension System of Amphibious vehicle, I designed a wheel retracting suspension. Compared with other wheel retracting suspension, The structure has following advantage of simple structure, light-weight and Reliable performance. According to the characteristic of this structure, The stress analysis of the main components are conducted and the motor selected.

Wheel retracting suspension Structure of amphibious vehicle motor torque self locking

1006-8244(2017)02-038-03

U469.79

B