二阶奇摄动滞后型微分方程解的存在性

潘宇洋， 王晓云

(太原理工大学 数学学院， 山西 太原 030024)

二阶奇摄动滞后型微分方程解的存在性

潘宇洋， 王晓云

(太原理工大学 数学学院， 山西 太原 030024)

研究了一类二阶奇异摄动滞后型微分方程的边值问题. 首先利用摄动方法中展开的思想对滞后项进行处理, 将原系统转化为不含时滞项的近似系统. 然后在一定的假设条件下, 结合边界层位于t=1和t=0处这两种情形, 利用奇异摄动方法和微分不等式技巧等对于方程的解给出了相应的存在性定理: 在满足一定的条件下, 对于足够小的ε>0, 边值问题存在满足条件的解.

二阶微分方程; 奇异摄动; 时滞; 边界层; 微分不等式

0 引 言

众所周知, 在工程技术和科学问题的应用领域中, 很多系统都呈现奇异摄动现象[1], 如飞机和火箭系统[2], 厄尔尼诺现象[3]. 具有奇异摄动现象的系统可以用奇摄动微分方程来描述， 而研究该方程的理论就是摄动方法[4-5]. 近年来, 许多学者用微分不等式理论研究奇摄动微分方程(组)的问题, 取得丰硕的成果[6-7]. 此外, 许多系统(如控制系统)常常会建立带有时滞项的奇摄动微分方程, 即奇摄动滞后型泛函微分方程[8-10].

本文研究一类奇摄动滞后型泛函微分方程边值问题的解的存在性. 主要是采用展开方法处理时滞项, 再运用奇异摄动法及微分不等式技巧研究如下二阶时滞奇摄动微分方程的边值问题

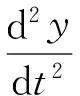
式中：ε是正的小参数(0<ε≪1)；r是一个很小的正数；B是常数； 函数f(t,y)在区间[0,1]×R上光滑.

1 预备知识

定义 1 函数α∈C2([a,b])为方程

的一个下解，如果

同样，函数β∈C2([a,b])是方程(3)的一个上解，如果

α(t)≤y(t)≤β(t).

2 存在性定理及证明

本文中的微分系统(1)～(2)是含有小参数ε的奇摄动滞后型微分系统. 本文利用文献[11-13]的思想(将滞后项展开转化为不含时滞项的等价系统)进行研究. 这里, 首先把式(1)中的y(t-r)项按r的幂展开, 即

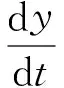
(6)

将式(6)代入式(1), 得到

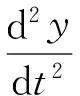
t∈[0,1].

由于r是一个非常小的正数, 而后面展开式中含有r2,r3, …的项是r的高阶无穷小, 在这里只保留到含r的一次幂这一项, 得到式(1)的近似系统, 即

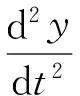
t∈[0,1].

(7)

相应的边值条件为

(8)

注： 由于r足够小(r>0), 那么在一定的范围内, 假设近似系统的解一致收敛于原问题的解. 这样, 研究问题(1)～(2)解的存在性转换为研究问题(7)～(8)的解的存在性. 即, 通过研究方程(7)～(8)的解的存在性对应得到方程(1)～(2)的解的存在性.

假设下面几个条件成立.

H1) 函数f(t,y)在区间 [0,1]×R上是C1-光滑的.

H2) 存在一个正数σ0满足f(t,y)≥σ0+r>0.

H2′) 存在一个正数σ0满足f(t,y)≤σ0-r<0.

H3) 方程(7)的退化问题

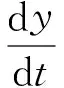
有一个解y=φ(t)∈C2([0,1]).

注: 由于f(t,y)在t=1或t=0处含有边界层, 因此, 分f(t,y)>0和f(t,y)<0两种情况讨论(对于每一个系统, 首先要确定边界层在x=0处还是x=1处, Mohan K. Kadalbajoo[14]给出了一个确定边界层位置的总结). 下面分别讨论.

2.1 边界层位于t=1处

假设f(t,y)≥σ0+r>0在区间[0,1]上均成立, 其中σ0是一个正数(根据文献[14], 该假设下边界层在t=1附近).

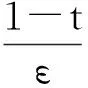
将y(t)=φ(t)+v(τ)代入式(7), 得到

φ(t)+v(τ)=0.

考虑边界层的零阶近似项, 有

相应的边界条件变成

由函数f(x,y)的连续性，有

σ1= max{f(1,φ(1)+v)+r∶-|B-φ(1)|≤

v≤|B-φ(1)|}.

为了方便证明主要结论, 先给出关于边界层问题(9)～(10)的估计解v0(t)的表达式和定义的引理.

引理 2 在假设H1)和H2)下, 对于足够小的ε>0, 边界层问题(9)～(10)有一个满足下面估计的解v0(τ).

且

|B-φ(1)|

其中

证明 首先选取辅助函数

易知

然后可得

α″(t)+f(1,φ(1)+α(τ))α′(τ)+rα′(τ)≥

(f(1,φ(1)+α(τ))+r))≥0.

同样可以得到

β″(t)+f(1,φ(1)+β(τ))β′(τ)+rβ′(τ)≤

(f(1,φ(1)+β(τ))+r))≤0.

根据引理1知, 方程(9)～(10)存在满足估计式(11)的解v0(τ).

下面证明式(12). 根据极限的定义和式(11), 得到下面的表达式

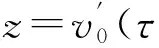
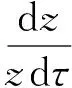
结合式(13), 并把上面的不等式从0到τ积分, 得到

|z(τ)|≤|B-φ(1)|

因此， 式(12)成立.

下面给出边界层在t=1处方程(7)～(8)的解的存在性定理.

定理 1 在条件H1),H2)和H3)成立的情况下, 对于足够小的ε>0, 边值问题(7)～(8)有满足下面条件的解

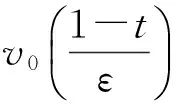
证明 由假设H1)和H3)知, 对足够小的ε>0, 存在一个正常数K, 使得

|φ′(t)|≤K, |φ″(t)|≤K,t∈[0,1],

|f(t,φ(t)+υ0(τ))-f(1,φ(1)+υ0(τ))≤

|fy(t,y)|≤K, (t,y)∈[0,1]×[A,B] .

首先根据渐近解的构造, 选取barrier函数

t∈[0,1],

t∈[0,1],

其中

以及

其中， 正常数L的取值会在下面的证明过程中给出.

容易得到以下几个命题:

i)

ii)

t∈[0,1],

t∈[0,1];

iii)v1(τ)是下面方程的解

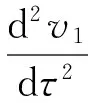
iv)γ(t)是下面方程的解

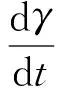
根据假设H1)～H3), 利用命题i)～iv), 得到下面的不等式

εα″(t)-f(t,α(t))α′(t)-rα′(t)+α(t)=

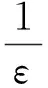
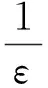
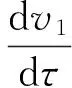
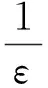
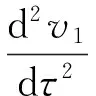
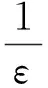
v0(τ) +[f(t,φ(t))-f(t,α(t))]φ′(t)+εφ″(t)+

(f(t,α(t))+r)γ′(t)ε-γ(t)ε-γ″(t)ε2-

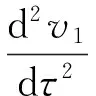
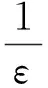
v0(τ)-fy(t,φ(t)+v0(τ)-εθ1v1(τ)-

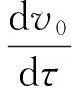
θ2v0(τ)-εθ2v1(τ)-εθ2γ(t))(v0(τ)-εv1(τ)-

εγ(t))φ′(t)+(f(t,α(t))+r)γ′(t)ε-γ(t)ε-

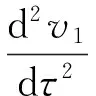
(K2-1)γ(t)ε-εK-γ″(t)ε2-

ε(K2-1)|v1(τ)|≥

选取

因此， 对足够小的ε>0, 有

εα″(t)-f(t,α(t))α′(t)-rα′(t)+α(t)≥0,

t∈[0,1].

同样, 对于足够小的ε>0, 用类似的方法得到

εβ″(t)-f(t,β(t))β′(t)-rβ′(t)+β(t)≤0,

t∈[0,1].

因此， 存在满足下面条件的解

显然有

α(t)≤β(t),t∈[0,1],α,β∈C1([0,1]),

α(0)≤A≤β(0),α(1)≤B≤β(1).

这样， 就证明了当边界层位于t=1处问题(7)～(8)解的存在性. 由于问题(7)～(8)是问题(1)～(2)的近似系统, 也就说明了问题(1)～(2)的解的存在性.下面给出边界层位于t=0时的情形.

2.2 边界层位于t=0处

首先假设f(t,y)≤σ0-r<0在区间[0,1]上均成立, 其中σ0是一个正数(根据文献[14], 这种假设下边界层在t=0附近).

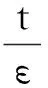
将y(t)=φ(t)+u(τ)代入式(7), 得到

φ(t)+u(τ)=0.

考虑边界层的零阶近似项, 有

相应的边界条件变成

下面给出边界层在t=0处方程(7)～(8)的解的存在性定理.

定理 2 在条件H1), H2′)和H3)成立的情况下, 对于足够小的ε>0, 边值问题(7)～(8)有满足下面条件的解

(19)

证明过程类似于定理1的证明, 此处略.

同样说明了问题(1)～(2)当边界层位于t=0处的解的存在性.

3 结 论

本文给出了一种研究奇摄动滞后型微分方程解的存在性方法, 用幂级数展开法把含有小参数ε的奇摄动滞后型微分方程边值问题(1)～(2)转换为不含时滞项的奇摄动微分方程边值问题(7)～(8), 通过研究问题(7)～(8)的解的存在性来研究(1)～(2)的解的存在性, 并根据边界层可能存在的位置(t=0或者t=1)分情形讨论. 在不同情形下, 给出解的存在性定理, 并利用微分不等式等技巧给出定理的证明.

[1]Roul P, Warbhe U. New approach for solving a class of singular boundary value problem arising in various physical models[J]. J Math Chem, 2016, 54: 1255-1285.

[2]Ardema M D. Singular perturbation in flight mechanics[M]. US: NASA, 1974.

[3]Du Z J, Lin W T, Mo J Q. Perturbation method of studying the EI Nio oscillation with two parameters by using the delay sea-air oscillator model[J]. Chin Phys B, 2012, 21(9): 090201.

[4]Holmes M H. Introduction to perturbation methods[M]. Singapore： World Scientific Publishing, 1999.

[5]Nayfeh A H. Introduction to perturbation techniques[M]. New York： John Wiley & Sons, 1981.

[6]Xie F. On a class of singular boundary value problems with singular perturbation[J]. J Differ Equations, 2012, 252(3): 2370-2387.

[7]周明儒, 杜增吉, 王广瓦. 奇异摄动中的微分不等式理论[M]. 北京： 科学出版社, 2012.

[8]Kudu M, Amirali I, Amiraliyev G M. A finite-difference method for a singularly perturbed delay integro-differential equation[J]. J Comput Appl Math, 2016, 308: 379-390.

[9]Humphries A R, Bernucci D A, Calleja R C. Periodic solutions of a singularly perturbed delay differential eqution with two state-dependent delays[J]. J Dyn Diff Equat, 2016, 28: 1215-1263.

[10]Chakravarthy P P, Kumar S D, Rao R N, et al. A fitted numerical scheme for second order singular perturbed delay differential equations via cubic spline in compression[J]. Adv Differ Equat, 2015, 2015(1): 1-14.

[11]Zhou X C, Shi L F, Mo J Q. A class of asymptotic solution for the time delay wind field model of an ocean[J]. Chin Phys B, 2014, 23(4): 040202.

[12]Wang W G, Lin W T, Shi L F, et al. Approximate solution of solitary wave for nonlinear-disturbed time delay long-wave system[J]. Acta Phys Sin, 2014, 63(11): 110204.

[13]Rao F, Wang W M, Li Z B. Hopf bifurcation analysis of a predator-prey system with delay and harvesting[J]. Journal of East China Normal University(Natural Science), 2010, 6: 186-198.

[14]Kadalbajoo M K, Patidar K C. A survey of numerical techniques for solving singularly perturbed ordinary differential equations[J]. Appl Math Comput, 2002, 130: 457-510.

Existence of Solutions of a Class of Singular Perturbation Second-Order Delay Differential Equation

PAN Yu-yang, WANG Xiao-yun

(College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)

The boundary value of a class of second-order singularly perturbed delaying differential equation is studied. First, by using the polynomial expansion in the perturbation method to the delayed terms, the original system is transformed into an equivalent system without delayed terms. Then, under certain hypothetic conditions, different existing theorems can be given according to the positions of the boundary layers which is located att=1 ort=0, through the singular perturbation method and the differential inequality technique. The theorem is: Under certain conditions, the boundary value has a solution to satisfy the condition ifε>0 is small enough.

second-order differential equations; singular perturbation; delay; boundary layer; differential inequality

1673-3193(2017)04-0404-05

2016-11-24

国家自然科学基金青年基金资助项目(11401420)； 山西省自然科学基金资助项目(201601D102002)； 太原理工大学2016年校专项/青年基金(2015MS033)； 太原理工大学引进人才基金资助项目(tyut-rc201317a)

潘宇洋(1991-)， 女， 硕士生， 主要从事摄动微分方程及应用的研究.

王晓云(1972-)， 女， 副教授， 博士， 主要从事摄动微分方程及应用的研究.

O175.8

A

10.3969/j.issn.1673-3193.2017.04.002