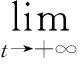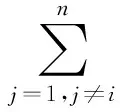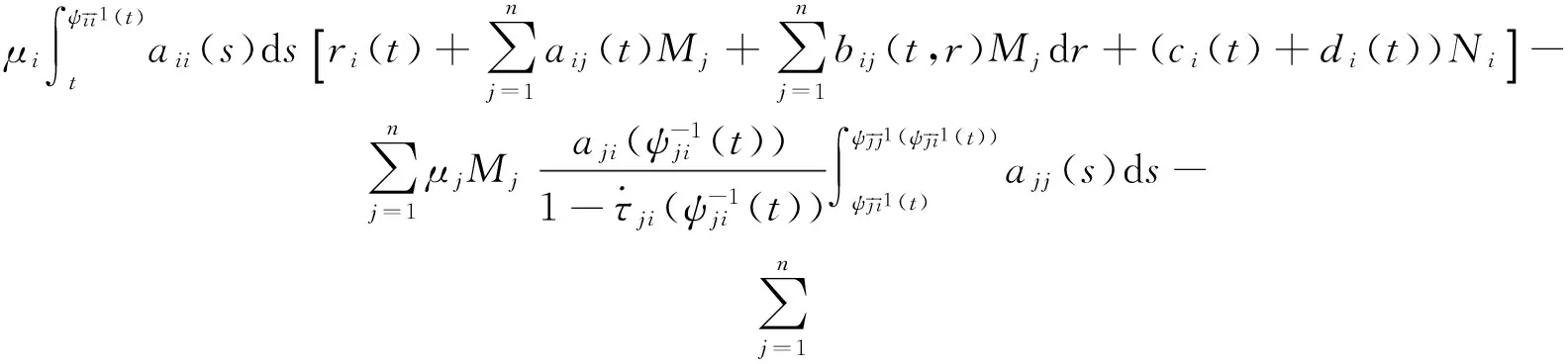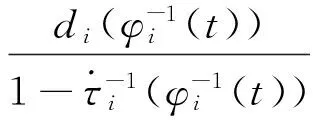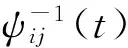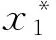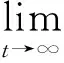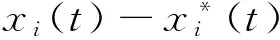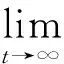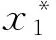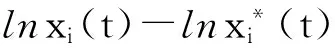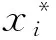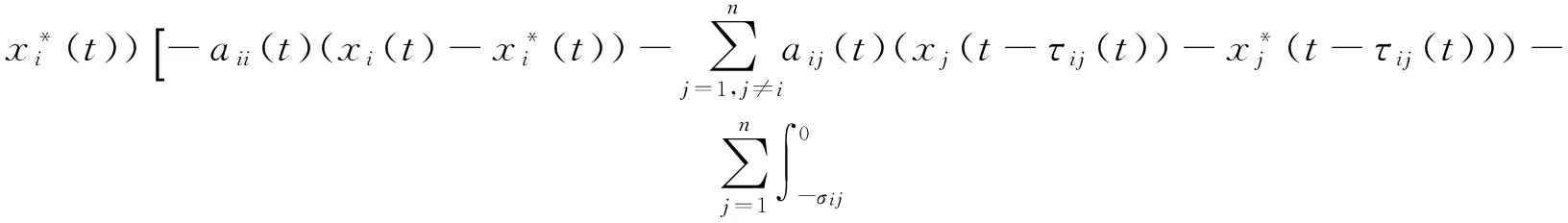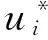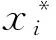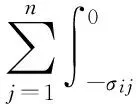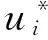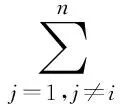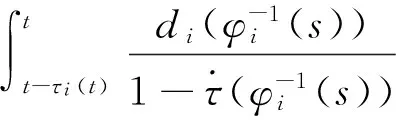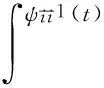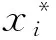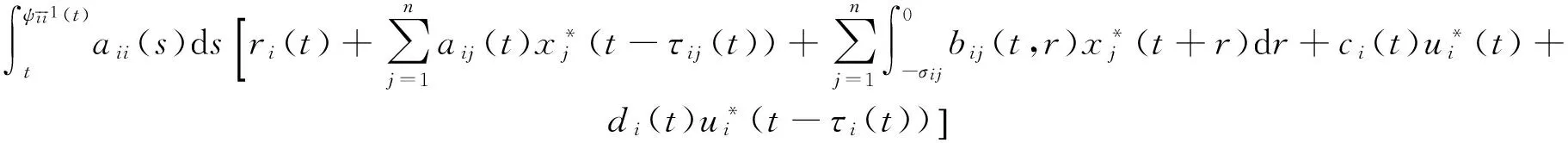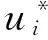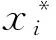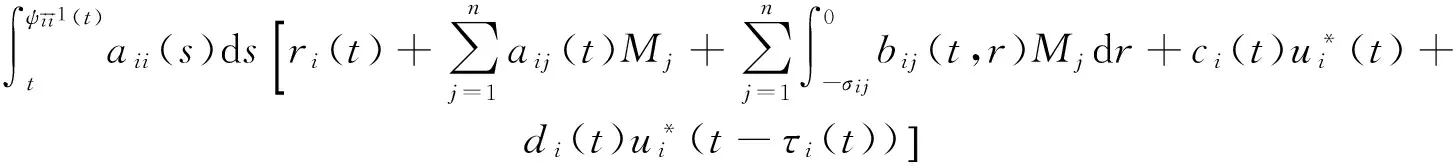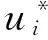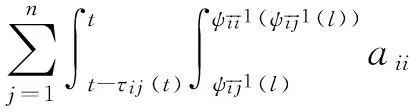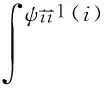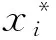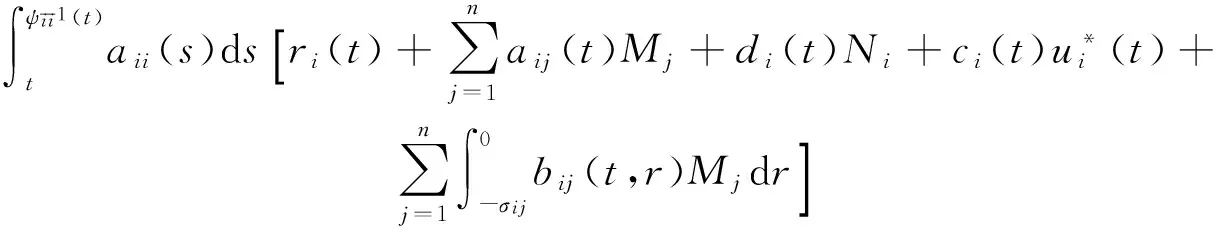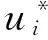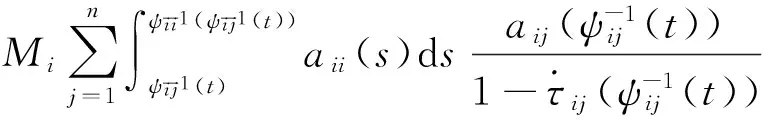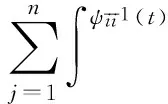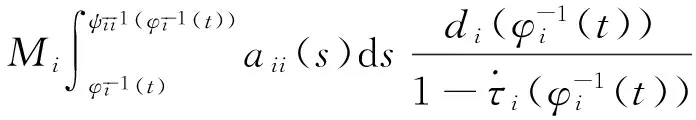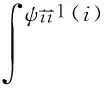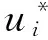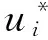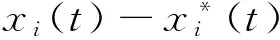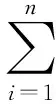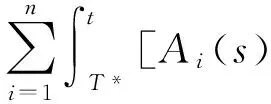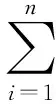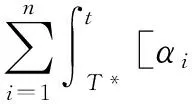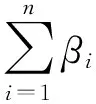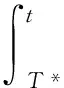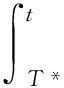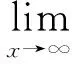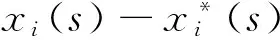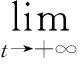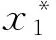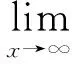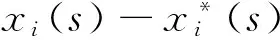具有反馈控制的Lotka-Volterra竞争系统的全局吸引性

程永玲， 王丽丽

(山西大学商务学院 基础教学部， 山西 太原 030031)

具有反馈控制的Lotka-Volterra竞争系统的全局吸引性

程永玲， 王丽丽

(山西大学商务学院 基础教学部， 山西 太原 030031)

研究了一类具有时滞和反馈控制的非自治n种群Lotka-Volterra竞争系统. 通过构造合适的Lyapunov泛函的方法， 得到了该系统的所有正解全局吸引的充分条件. 所得结论将已有文献的结果推广至时滞反馈控制系统， 具有一定的理论意义和较强的实际应用价值. 所得到的结果是新的.

非自治；反馈控制；全局吸引；Lyapunov泛函

0 引 言

经典的Lotka-Volterra系统是一类非常重要的生态系统， 已经有大量的研究结果[1-5]. 众所周知， 生态系统中的种群经常会受到来自外界各种因素的影响， 从而导致生态系统的各种参数的变化. 实验表明， 通过反馈控制的方法能够得到非常理想地消除外界干扰的效果. 因此， 反馈控制对于保护生物的种群多样性、维持生态环境的可持续发展有着重要的意义. 文献[4-5]研究了具有时滞和反馈控制的非自治Lotka-Volterra竞争系统， 利用Lyapunov泛函和新的分析方法， 分别得到了系统(1)持久和部分种群灭绝的充分条件.

文献[6]考虑了具有时滞和反馈控制的非自治多种群Lotka-Volterra系统， 通过构造合适的Lyapunov泛函得到了系统(2)全局吸引的充分条件.

文献[9]研究了Lotka-Volterra竞争系统的灭绝性， 文献[10]研究了捕食-被捕食系统. 文献[11-14]研究了具有时滞的Lotka-Volterra系统的稳定性. 受到这些文献的启发， 特别是文献[4-6]的启发， 本文将考虑具有反馈控制的Lotka-Volterra竞争系统(1)的全局吸引性. 通过改进文献[7-8]的方法， 得到系统(1)正解全局吸引性的充分条件.

1 预备知识

以下如不加特别说明则i,j=1,2,…,n.

本文对系统(1)假定：

H1：ri(t),aij(t),ci(t),di(t),ei(t),

fi(t),gi(t)为[0,+∞)上的有界连续函数， 且aij(t),ci(t),di(t),ei(t),fi(t),gi(t)为[0,+∞) 上的非负函数；

H3：bij(t,s)在[0,+∞)×[-σij,0]上关于t∈[0,+∞) 连续且关于s∈[-σij,0]可积， 对任意(t,s)∈[0,+∞)×[-σij,0]有

0≤bij(t,s)≤h0(s),

其中,h0(s)是某一给定的定义在[-τ,0]上的可积函数， 且

τ=sup{τij(t),τi(t),δi(t),σij∶t∈[0,+∞)}.

H4： 存在正常数ω和λ使得

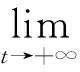
H5： 存在正常数β和γ使得

根据系统(1)代表的生态学背景,考虑系统(1)满足如下初始条件的解

式中：φi,ψi是给定的定义在θ∈[-τ,0]上非负有界连续函数, 并且φi(0)>0,ψi(0)>0. 由泛函微分方程的基本理论可知, 对任何初始函数

φ=(φ1,φ2,…,φn),ψ=(ψ1,ψ2,…,ψn),

系统(1)存在唯一的解满足初始条件,并且容易证明解是正的[3].

2 主要结论

与文献[5]引理2.2的证明类似， 可得

引理 1 假定H1～H5成立， 则对系统(1)的任意正解， 存在正常数Mi,Ni,T， 使得当t≥T时， 有

0

定理 1 假定H1～H5成立, 且存在正常数μi,ki， 使得

其中

(x1(t),…,xn(t),u1(t),…,un(t)),

有

证明 设

(x1(t),…,xn(t),u1(t),…,un(t))，

是系统(1)和(3)的任意两个正解. 由引理1知， 存在正常数Mi,Ni,T， 使得当t≥T时， 有

沿着系统(1)和(3)的解计算Vi1(t)的右上导数， 得

将方程(1)代入式(5)并整理， 可得

将系统(1)代入式(6)， 经计算， 有

放大式(7)， 可得

D+Vi1(t)≤

Vi2(t)=

结合式(8)， 由引理1， 有

定义Vi(t)=Vi1(t)+Vi2(t)+Vi3(t). 因此， 当t≥T+τ时，

进一步， 令

计算可得

构造Lyapunov泛函

由式(9)～式(11)可知， 当t≥T+τ时，

由条件(4)可知， 存在正常数αi,βi,T*≥T， 使得当t≥T*时，

在区间[T*,t]上积分式(12)， 可得

V(T*)≥V(t)+

由式(13)和式(14)， 可知

V(T*)≥V(t)+

因此， V(t)在[T*,∞)上有界， 且

由Barbalat’s[10]引理， 可得

证毕.

系统(1)退化为无时滞非自治Lotka-Volterra系统

推论 1 设条件H1， H4～H5成立， 且存在正常数μi, ki， 使得

其中

ki(fi(t)+gi(t)),

Bi(t)=kiei(t)-μidi(t).

则对系统(15)的任意两个正解

(x1(t),…,xn(t),u1(t),…,un(t)),

有

注 将推论1与[1]中定理2.1进行比较， 定理1可看成将[1]中定理2.1推广至时滞系统上.

[1]ChenFengde.ThepermanenceandglobalattractivityofLotka-Volterracompetetionsystemwithfeedbackcontrols[J] .NonlinearAnalRWA， 2006， 7(1)： 133-143.

[2]TengZhidong，YuYuanhong.SomenewresultsofnonautonomousLotka-Volterracompetitivesystemswithdelays[J].J.Math.Anal.Appl.， 2000， 241(2)： 254-275.

[3]滕志东. 具有时滞的非自治Lotka-Volterra竞争系统的持久与灭绝[J]. 数学学报， 2001， 44(2)： 293-306.TengZhidong.OnthepermanenceandextinctioninnonautonomousLotka-Volterracompetitivesystemswithdelays[J].ActaMathematicaSinica， 2001， 44(2)： 293-306. (inChinese)

[4]HuHongxiao，TengZhidong，JiangHaijun.OnthepermanenceinnonautonomousLotka-Voltrracompetitivesystemwithpure-delaysandfeedbackcontrols[J].NonlinearAnalRWA， 2009， 10(3)： 1803-1815.

[5]HuHongxiao，TengZhidong，GaoShujing.ExtinctioninnonautonomousLotka-Volterracompetitivesystemwithpure-delaysandfeedbackcontrols[J].NonlinearAnalRWA， 2009， 10(4)： 2508-2520.

[6]NieLinfei，PengJigen，TengZhidong.Peramnenceandstabilityinmulti-speciesnon-autonomousLotka-Volterracompetitivesystemswithdelaysandfeedbackcontrols[J].MathComputModelling， 2009， 49(1-2)： 295-306.

[7]QiWang，DaiBingxiang.Almostperiodicsolutionforn-speciesLotka-Voltrracompetitivesystemwithdelayandfeendbackcontrols[J].ApplMathComputer， 2008， 200(1)： 133-146.

[8]ChenFengde.PermanenceinNonautonomousmulti-speciespredator-preysystemwithfeedbackcontrols[J].ApplMathComput， 2006， 173(2)： 694-709.

[9]王丽丽. 一类时滞非自治Lotka-Volterra竞争系统的灭绝性[J]. 生物数学学报， 2009， 24(1)： 81-86.WangLili.ExtinctiononnonautonomousLotka-Volterratypecompetitivesystemswithdelay[J].JournalofBiomathematics， 2009， 24(1)： 81-86. (inChinese)

[10]ChenLiujuan，ChenFengde，WangYiqin.InfluenceofpredatormutualinterferenceandpreyrefugeonLotka-Volterrapredator-preydynamics[J].CommunicationsinNonlinearScienceandNumericalSimulation， 2013， 18(11)： 3174-3180.

[11]YuJuan,HuCheng,JiangHaijun,etal.Stabilizationofnonlinearsystemswithtime-varyingdelaysviaimpulsivecontrol[J].Neurocomputing， 2014， 125： 68-71.

[12]WeiZheng，SugieJitsuro.AnecessaryandsufficientconditionforglobalasymptoticstabilityoftimevaryingLotka-Volterrapredator-preysystems[J].NonlinearAnalysis， 2015， 127： 128-142.

[13]LiJinxian，ZhaoAimin.Stabilityanalysisofanon-autonomousLotka-Volterracompetitionmodelwithseasonalsuccession[J].AppliedMathematicalModelling， 2016， 40： 763-781.

[14]HouZhanyuan.PermanenceandextinctionincompetitiveLotka-Volterrasystemswithdelays[J].NonlinearAnalRWA， 2011， 12: 2130-2141.

[15]GopalsamyK.Stabilityandoscillationsindelaydifferentialequationsofpopulationdynamics[M].Dordrecht：KluwerAcademic， 1992.

Global Attractivity of Lotka-Volterra Competitive System with Feedback Controls

CHENG Yong-ling, WANG Li-li

(Basic Course Department, Business College of Shanxi University, Taiyuan 030031, China)

Annspecies Lotka-Volterra competitive systems with delays and feedback controls was considered. By constructing suitable Lyapunov functional, sufficient conditions for global stability of the system were obtained. The conclusion extends the results of the existing literature to delay and feedback control system and provide more theoretical significance and applicable value. The conclusion is new.

non-autonomous； feedback controls； global stability； Lyapunov function

1673-3193(2017)04-0414-06

2016-11-28

程永玲(1980-)， 女， 讲师， 硕士， 主要从事动力系统方面的研究.

O17514

A

10.3969/j.issn.1673-3193.2017.04.004