一类改进的人工蜂群算法

胡红萍， 崔霞霞， 续 婷， 白艳萍

(中北大学 理学院， 山西 太原 030051)

一类改进的人工蜂群算法

胡红萍， 崔霞霞， 续 婷， 白艳萍

(中北大学 理学院， 山西 太原 030051)

对2005年Karaboga提出的模仿蜜蜂觅食行为的人工蜂群算法进行了研究， 将粒子群算法中的惯性权重引入到人工蜂群算法中， 提出了带惯性权重的改进的人工蜂群算法(Improved artificial bee colony algorithm with inertia weight,ABCIW)的方法. 将ABCIW算法应用于求解基准函数的最小值问题， 进而应用于优化BP神经网络的参数， 对中国手足口病发病人数进行预测. 与基本人工蜂群算法、 快速人工蜂群算法和带记忆的人工蜂群算法相比较， ABCIW算法更适合解决函数的优化问题. 对中国手足口病发病人数的预测说明了ABCIW算法具有较好的预测结果和较高的稳定性.

人工蜂群算法； 基准函数； 手足口病； 预测

0 引 言

2005年由Karaboga[1]提出的人工蜂群算法(Artificial bee colony algorithm, ABC)是一种模拟蜜蜂觅食行为的群智能算法. ABC 算法的优点在于仅有三个可调节参数： 种群大小， 最大循环次数和搜索最大参数. 研究学者已经成功地将ABC算法应用于很多方面， 例如聚类[2], 函数优化问题[3-6]， 优化神经网络[7], 最优能量流[8], 无线传感网络[9]和医药科学[10].

根据功能性的不同， ABC算法包括雇佣蜂， 跟随蜂和侦查蜂三个阶段. 许多学者集中在雇佣蜂和跟随蜂的邻域搜索和侦查蜂的探索参数limit. 现在已经存在很多改进的ABC算法， 例如由GABC[4], qABC[11], FABC[5], MuABC[12], ABCM[3].In ABC和大多数改进的ABC， 在邻域搜索中采用轮盘赌选择策略.

在神经网络中， 好的权值和偏差能让神经网络运行得到好的结果. 因此， 许多研究人员提出许多优化算法， 例如正交最小二乘法[13-15]， 聚类算法[16]， 遗传算法(GA)[17-19]， 蚁群优化算法(ACO)[20-22]， 粒子群算法[23-26]和人工蜂群算法(ABC)算法[7]. BP神经网络是一种有效的反馈神经网络， 经常用于预测应用[26]. 一般BP神经网络包括输入层， 隐含层和输出层， 结构为r-h-s模型， 其中r表示输入层中输入节点的个数，h表示隐含层中节点的个数，s表示输出层中节点的个数.

本文将粒子群算法(Particle swarm optimization, PSO)中的惯性权重引入到ABC算法， 得到新的算法， 命名为ABCIW算法. 引入4种惯性权重： 线性递减惯性权重(LDIW)[27]， 非线性递减惯性权重(NDIW)[28]， Sugeno函数惯性权重(SFIW)[29]和指数递减惯性权重(EDIW)[30]， 相应的ABCIW算法为ABCLDIW,ABCNDIW,ABCSFIW,ABCEDIW算法. 进而将ABCIW算法用于优化BP神经网络的权值和偏差来实现手足口病(HFMD)的发病人数预测， 得到ABC-BP ,ABCLDIW,ABCNDIW,ABCSFIW和ABCEDIW模型.

1 基本人工蜂群算法(ABC)

ABC算法根据功能不同包括雇佣蜂， 非雇佣蜂和食物源， 其中雇佣蜂与食物源相对应， 非雇佣蜂包括跟随蜂和侦查蜂. 这样， 种群就由雇佣蜂、 跟随蜂和侦查蜂构成. 将一个食物源代表问题的一个可能解， 食物源的花蜜代表解对应的目标函数值. 这样在雇佣蜂和食物源之间存在一一对应关系. 每只雇佣蜂在其邻域内寻找新的食物源并利用轮盘赌方式选择食物源. 与雇佣蜂不同， 按照一定的概率， 跟随蜂根据花蜜质量选择较好的食物源， 选择的方式类似于雇佣蜂. 经过一定数量的选择(控制参数limit),食物源的花蜜保持不变， 这时将抛弃该食物源， 相应的雇佣蜂变为侦查蜂， 寻找新的食物源， 找到后此侦查蜂又变为雇佣蜂.

在ABC算法中， 雇佣蜂的数量或跟随蜂的数量等于食物源的个数, 因此ABC算法有3个参数： 食物源的个数SN， 最大迭代次数MCN， 控制参数limit. ABC算法具体描述如下.

1.1 初始化

ABC算法中， 第ith食物源是随机产生的D维向量xi=(xi1,xi2,…,xiD) (i=1,2,…,SN)， 其中

式中：rand(0,1)表示[0,1]中的随机数， 其下界和上界分别为

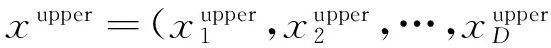
1.2 雇佣蜂

每只雇佣蜂xi(i=1,2,…,SN)利用式(2)进行邻域搜索产生新的食物源vi(i=1,2,…,SN).

式中：k是不同于i的任意数；φij是[-1,1]中的任意数.

若xi的花蜜优于vi的花蜜， 则第i只雇佣蜂保持当前的食物源xi， 否则第i只雇佣蜂选择新的食物源vi， 并抛弃旧的食物源xi.

1.3 概率计算

在所有的雇佣蜂完成邻域搜索后， 跟随蜂与雇佣蜂分享食物源. 跟随蜂与雇佣蜂根据轮盘赌选择食物源. 跟随蜂选择食物源xi的概率为

式中：fitness(i)表示第i个食物源的适应度值.

式中：fi是食物源xi的目标函数值.

1.4 跟随蜂

按照上述所提到的概率pi, 每只跟随蜂选择与雇佣蜂分享的食物源， 其邻域搜索的方式类似于雇佣蜂的搜索方式.

1.5 侦查蜂

当食物源被雇佣蜂和跟随蜂多次访问也没有发生改进， 就抛弃了该食物源， 相应的雇佣蜂变为侦查蜂. 新的食物源由式(1)产生代替旧的食物源. 这样侦查蜂变为雇佣蜂.

1.6 基本ABC算法

ABC算法的步骤：

1) 给出参数： 食物源的个数SN, 最大循环次数MCN和控制参数limit；

2) 初始化种群；

3) 对于每只雇佣蜂xj完成其邻域搜索， 由式(2)获得新的食物源vj， 由轮盘赌选择策略确定较好的雇佣蜂xj.

4) 根据式(3)计算食物源xi(i=1,2,…,SN)的概率pi， 根据概率从现有解的邻域中搜索新的解并按照轮盘赌选择策略进行选择；

5) 判断食物源的更新失败次数是否超过了预先设定的控制参数limit, 若是， 就抛弃该食物源， 用式(1)产生新的食物源代替它；

6) 判断循环是否达到MCN, 若是则终止， 否则返回步骤3.

2 本文的带有惯性权重的ABC算法

2.1 由反向学习初始化

最后根据初始解和反向解的适应度值选择前SN个解形成初始种群.

2.2 邻域搜索

本文中， 雇佣蜂和跟随蜂的邻域搜索方式是由

确定的， 其中k是不同于i的任意数，φij是[-1,1]中的任意数，ω∈[0,1]是惯性权重. 当ω=1, 式(6)就是式(2)， 当ω随着迭代变化时, ABC算法就是动态ABC算法.

本文采用PSO算法中的四种惯性权重为

式中：t是目前的迭代次数；T是最大迭代次数；ωinitial是初始惯性权重；ωfinal是最终惯性权重；n是非线性指数；s是大于-1的常数；c>0是控制惯性权重收敛的控制参数. 相应的ABCIW算法就分别为ABCLDIW 算法, ABCNDIW 算法, ABCSFIW 算法和ABCEDIW算法.

2.3 侦查蜂

本文中， 侦查蜂寻找新的食物源是由

2.4ABCIW算法

ABCIW算法的步骤：

1) 初始化参数： ωinitial, ωfinal, c, n, SN, MCN, limit；

2) 基于反向学习初始化种群；

3) 对于每只雇佣蜂xj完成其邻域搜索， 由式(6)获得新的食物源vj， 由轮盘赌选择策略确定较好的雇佣蜂xj；

4) 根据式(3)计算食物源xi(i=1,2,…,SN)的概率pi， 根据概率从现有解的邻域中搜索新的解并按照轮盘赌选择策略进行选择；

5) 判断食物源的更新失败次数是否超过了预先设定的控制参数limit,若是， 就抛弃该食物源， 用式(11)产生新的食物源代替它；

6) 判断循环是否达到MCN, 若是则终止， 否则返回步骤3).

3 ABCIW- BP模型

本文利用ABC算法和ABCIW算法优化BP神经网络的权值和偏差， 建立了基于ABC算法和ABCIW算法的BP神经网络模型， 即ABC-BP模型,ABCIW-BP模型. 根据惯性权重的不同，ABCIW算法又分为ABCLDIW,ABCNDIW,ABCSFIW和ABCEDIW算法. 相应地，ABCIW-BP模型又分为ABCLDIW-BP模型，ABCNDIW-BP模型,ABCSFIW-BP模型和ABCEDIW-BP模型.

上述模型的目标函数定义为

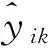
ABC-BP模型和ABCIW-BP模型的步骤:

1) 初始化参数: 非线性调节指数n, 控制参数c, 最初惯性权重ωinitial, 最终惯性权重ωfinal,limit和常数s, 最大迭代次数MCN, 和食物源的个数SN. 对于ABC-BP用式(4)， 对于ABCIW-BP用式(8)初始化每个食物源.

2) 将输入样本归一化.

3) 将每个食物源映射到BP神经网络的参数.

4) 由式(12)计算每只雇佣蜂的目标函数和由式(4)计算每只雇佣蜂的适应度值. 选择每只雇佣蜂的当前的适应度值作为其局部最优值. 整个蜂群的适应度值的最小值作为全局最优值.

5) 在ABC-BP模型中每只雇佣蜂利用式(2)实现邻域搜索， 运用轮盘赌选择策略产生新的食物源， 而在ABCIW-BP模型中每只雇佣蜂利用式(6)实现邻域搜索， 运用轮盘赌选择策略产生新的食物源. 将每个食物源映射到BP神经网络的参数. 重新计算雇佣蜂的局部最优质和全局最优值.

6) 对于每只跟随蜂， 在ABC-BP模型中利用式(2)实现邻域搜索， 运用轮盘赌选择策略产生新的食物源， 而在ABCIW-BP模型中利用式(6)实现邻域搜索， 运用轮盘赌选择策略产生新的食物源. 每个食物源映射到BP神经网络的参数. 重新计算雇佣蜂的局部最优质和全局最优值.

7) 判断食物源的更新失败次数是否超过了预先设定的控制参数limit， 若是， 就抛弃该食物源， 用式(1)或式(11)产生新的食物源代替.

8) 迭代次数低于MCN， 转步骤5).

4 实验结果

4.1 优化基准函数

本文选取表 1 中所示的4个基准函数验证所提出的ABCIW算法的有效性， 并与基本ABC算法、 带记忆的人工蜂群算法(ABCM算法)[3]和快速人工蜂群算法(qABC算法)[11]进行比较.

表 1 本文中所选取的4个基准函数

选择食物源的数量SN=25， 最大迭代次数MCN=10 000， 侦查蜂的控制参数

非线性调节参数n=1.2， 常数s=0.3， 控制参数c=6， 最初惯性权重和最终惯性权重分别为ωinitial=0.9,ωfinal=0.2. 对于每个函数， 对立运行30次， 取均值， 得到表 2 的结果.

由表 2 可以看出， ABCLDIW， ABCNDIW和ABCSFIW算法比ABC， ABCM和qABC算法更适合解决函数f1，f2，f3，f4的优化问题. 通过比较， ABCSFIW算法实现的函数f1和f4的最小值的平均值为3.23134e -16， ABC， ABCIW， ABCM和qABC算法实现的函数f2的最小值的平均值均为0， ABCNDIW和ABCSFIW算法实现的函数的最小值的平均值均为0. 因此 可以说明本文提出的ABCIW算法适合函数的优化问题.

表 2 ABCIW, ABC, ABCM和qABC的比较

4.2 手足口病预测

本文选取中国2010年2月到2016年3月的手足口病的发病人数进行实时预测. 取5天的发病人数预测第6天的发病人数， 这样建立了69组数据， 再取最后的8组数据作为测试数据， 其余数据作为训练数据. 首先将这69组数据进行归一化， 采用的方法为

式中：x为归一化之前的原始数据;xmin和xmax分别表示归一化之前原始数据的最小值和最大值;y为归一化之后的结果;ymin和ymax分别表示归一化后数据的最小值和最大值.

为了更准确地评估ABC-BP和ABCIW-BP模型的性能， 本文采用均方差(MSE)、 相对均方误差(RMSE)、 平均绝对百分比误差(MAPE)作为评价指标， 定义如下

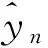
通过大量的实验和误差分析， 选择BP神经网络的结构为5-10-1预测手足口病的发病人数. 因此， 在ABC-BP模型和ABCIW-BP模型中， 每个食物源的维数是71. 在ABC-BP模型和ABCIW-BP模型中， 参数n,c,ωinitial,ωfinal,s的选取与 4.1节中一致.

ABC-BP和ABCIW-BP模型对手足口病发病人数的网络训练输出的 MSE、 RMSE和MAPE(%)3种评价指标结果如表 3 所示. 从表中可以看出， ABCNDIW-BP模型训练输出的3种评价指标 MSE(*e+9)、 RMSE和MAPE(%)的结果分别为4.015 7, 0.151 1, 0.318 8， 都是最小的.

表 3 ABC-BP和ABCIW-BP模型训练输出的手足口病发病人数的MSE， RMSE和MAPE(%)值

利用训练好的 BP神经网络对 2015年8月至2016年3月共8个月的中国手足口病发病人数进行预测， ABC-BP和ABCIW-BP模型的预测值如表 4 所示， 预测值与实际值之间的 MSE、 RMSE和 MAPE(%)这3种评价指标结果如表 5 所示.

由表 5 可以看出， ABCSFIW-BP模型的3种预测评价指标MSE、 RMSE和MAPE(%)的结果分别为 5.537 8， 0.327 8， 0.545 5， 都是最小的. 综合表 3 和表 5 可以看出， ABCIW-BP模型的3种训练和预测评价指标MSE、 RMSE和MAPE(%)均比ABC-BP模型小. 表明本文提出的ABCIW-BP模型适用于手足口病发病人数的预测.

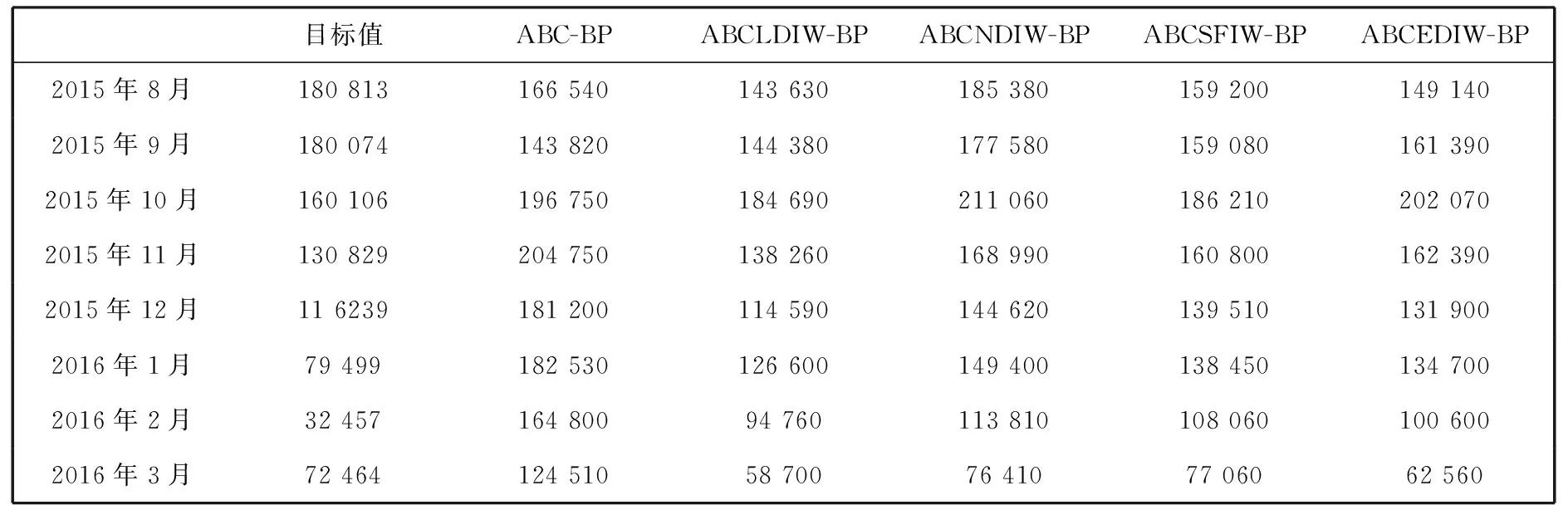
表 4 手足口病发病人数的ABC-BP和ABCIW-BP模型预测结果

表 5 ABC-BP和ABCIW-BP模型预测输出的手足口病发病人数的MSE， RMSE和MAPE(%)值

5 结 论

本文在ABC 算法基础上对人工蜂群算法进行了改进， 采用基于反向学习的群体初始化方案， 使初始解尽可能均匀分布在搜索空间， 增强了初始群体的多样性;在局部搜索中， 引入了4种递减的惯性权重， 不断增强了局部寻优能力， 这就是带有惯性权重的ABC算法——ABCIW算法， 并将其应用于优化4个基准函数和优化BP神经网络的连接权值与偏差来实现手足口病发病人数的预测. 结果表明， ABCIW算法更适合解决函数的优化问题， ABCIW-BP模型具有较好的预测结果和较高的稳定性.

[1]Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report-TR06, 2005.

[2]Forsati R, Keikha A, Shamsfard M. An improved bee colony optimization algorithm with an application to document clustering[J]. Neurocomputing, 2015， 159： 9-26.

[3]Li Xianneng， Yang Guangfei. Artificial bee colony algorithm with memory[J]. Applied Soft Computing， 2016， 41： 362-372.

[4]Zhu Guopu， Sam Kwong. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation. 2010， 217 (7)： 3166-3173.

[5]Phuc Nguyen Hong， Chang Wook Ahn. Fast artificial bee colony and its application to stereo correspondence[J]. Expert Systems with Applications， 2016， 45： 460-470.

[6]Anuar S， Selamat A， Sallehuddin R. A modified scout bee for artificial bee colony algorithm and its performance on optimization problems[J]. Journal of King Saud University-Computer and Information Sciences， 2016， 28(4)： 395-406.

[7]Karaboga D. Artificial bee colony algorithm[J].Scholarpedia， 2010， 5(3)： 6915.

[8]Jadhav H T， Bamane P D. Temperature dependent optimal power flow usingg-best guided artificial bee colony algorithm[J]. Electrical Power and Energy Systems， 2016， 77： 77-90.

[9]Hashim H A， Ayinde B O， Abido M A. Optimal placement of relay nodes in wireless sensor network using artificial bee colony algorithm[J]. Journal of Network and Computer Applications， 2016， 64： 239-248.

[10]JoséA.Delgado-Osuna， Manuel Lozano， Carlos García-Martínez. An alternative artificial bee colony algorithm with destructive -constructive neighborhood operator for the problem of composing medical crews[J]. Information Sciences， 2016， 326： 215-226.

[11]Karaboga D， Gorkemli B. A quick artificial bee colony (qABC) algorithm and its performance on optimization problems[J]. Applied Soft Computing， 2014， 23： 227-238.

[12]Gao Weifeng， Huang Lingling， Liu Sanyang， et al. Artificial bee colony algorithm with multiple search strategies[J]. Applied Mathematics and Computation， 2015， 271： 269-287.

[13]Chen S L， Cowan C N， Grant P M. Orthogonal least squares learning algorithm for radial basis function networks[J]. IEEE Transactions on Neural Networks， 1991， 2(3)： 302-309.

[14]Tianshi Chen， Lennart Ljung. Implementation of algorithms for tuning parameters in regularized least squares problems in system identification[J].Automatica， 2013， 49： 2213-2220.

[15]Zhu Q M. An implicit least squares algorithm for nonlinear rational model parameter estimation[J]. Applied Mathematical Modeling， 2005， 29： 673-689.

[16] Grabusts P S. A study of clustering algorithm application in RBF neural networks[J]. Scientific Proceedings of Riga Technical University, 2001： 50-57.

[17]Soltanali S， Halladj R， Tayyebi S, et al. Neural network and genetic algorithm for modeling and optimization of effective parameters on synthesized ZSM-5particlesize[J].Materials Letters， 2014， 136： 138-140

[18]Maria Beatriz Takahashi， José Celso Rocha， Eutimio Gustavo Fernández Núez. Optimization of artificial neural network by genetic algorithm for describing viral production from uniform design data[J]. Process Biochemistry， 2016， 51： 422-430.

[19]Billings S A， Zheng G L. Radial basis function network configuration using genetic algorithms[J]. Neural Networks， 1995， 8(6)： 877-890.

[20]Jie Zhang， Yiting Feng， Mahmood Hilal Al-Mahrouqi. Reliable optimal control of a fed-batch fermentation process using ant colony optimization and bootstrap aggregated neural network models[J]. Computer Aided Chemical Engineering， 2011， 29： 663-667.

[21]Lu Hungching， Liu Hsikuang. Ant colony fuzzy neural network controller for cruising vessel on river[J]. Applied Ocean Research， 2013， 42： 43-54.

[22]Man Chuntao， Li Xiaoxia， Zhang Liyong. Radial basis function neural network based on ant colony optimization[C]//Proceedings of the International Conference on Computational Intelligence and Security Workshops (CIS’07). Harbin, China, 2007： 59-62.

[23]Chen Sheng， Hong Xia， Bing Lam Luk， et al. Non-linear system identification using particle swarm optimization tuned radial basis function models[J]. International Journal of Bio-Inspired Computation， 2009， 1(4)： 246-258.

[24]Wu Defeng， Warwick K， Ma Zi， et al. Prediction of parkinson’s disease tremor onset using a radial basis function neural network based on particle swarm optimization[J]. International Journal of Neural Systems， 2010， 20(2)： 109-116.

[25]Ren Chao， An Ning， Wang Jianzhou， et al. Optimal parameters selection for BP neural network based on particle swarm optimization： a case study of wind speed forecasting[J]. Knowledge-Based Systems， 2014， 56： 226-239.

[26]Cheng Cheng， Cheng Xiaosheng， Dai Ning， et al. Prediction of facial deformation after complete denture prosthesis using BP neural network[J].Computers in Biology and Medicine， 2015， 66： 103-112.

[27]Shi Yuhui， Eberhart R. A modified particle swarm optimizer[C]. Proceedings of the 1998 IEEE International Conference on Evolutionary Computation (ICEC’98)， 1998： 69-73.

[28]Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers and Operations Research， 2006， 33(3)： 859-871.

[29]Lei K, Qiu Y, He Y. A new adaptive well-chosen inertia weight strategy to automatically harmonize global and local search ability in particle swarm optimization[C]. First International Symposium on Systems and Control in Aerospace and Astronautics. 2003. ISSCAA 2006. Harbin: IEEE, 2006： 7.

[30]Lu Jinna， Hu Hongping， Bai Yanping. Radial basis function neural network based on an improved exponential decreasing inertia weight-particle swarm optimization algorithm for AQI prediction[EB/OL]. (2014-01-12)[2016-09-30]. http:∥dx.doi.org/10.1155/2014/17813.

A Kind of Improved Artificial Bee Colony Algorithm

HU Hong-ping, CUI Xia-xia, XU Ting, BAI Yan-ping

(School of Science, North University of China, Taiyuan 030051, China)

Artificial bee colony algorithm presented by Karaboga in 2005 is researched, which imitates the foraging behavior of honeybees. An inertia weight in particle swarm optimization is introduced into artificial bee colony algorithm, and an improved artificial bee colony algorithm with inertia weight(ABCIW) is proposed. Apply ABCIW algorithm to solve the minimum problems of benchmark functions and further to optimize the parameters of BP neural network for predicting the onset number of hand-foot-mouth disease in China. By comparison with basic artificial bee colony algorithm, quick artificial bee colony algorithm and artificial bee colony algorithm with memory, ABCIW algorithm is more suitable for solving the optimization problems of functions. The prediction results of the onset number of hand-foot-mouth disease in China show that ABCIW algorithm has good prediction results and higher stability.

artificial bee colony algorithm; benchmark function; hand-foot-mouth disease; prediction

1673-3193(2017)04-0397-07

2016-09-30

国家自然科学基金资助项目(61275120)

胡红萍(1973-)， 女， 副教授， 硕士生导师， 主要从事工程中的数学问题的研究.

TP301.6

A

10.3969/j.issn.1673-3193.2017.04.001