带有脉冲的二阶多点微分方程的边值问题
李海艳, 郭宇恒, 李利玫
(1. 四川大学锦城学院 数学教研室, 四川 成都 611731; 2. 电子科技大学 通信学院, 四川 成都 611731; 3. 四川师范大学 数学与软件学院, 四川 成都 610068)
带有脉冲的二阶多点微分方程的边值问题
李海艳1, 郭宇恒2, 李利玫3
(1. 四川大学锦城学院 数学教研室, 四川 成都 611731; 2. 电子科技大学 通信学院, 四川 成都 611731; 3. 四川师范大学 数学与软件学院, 四川 成都 610068)
研究了一类带有脉冲的二阶多点微分方程的边值问题, 将以往所研究的方程的脉冲项和边界条件做了推广, 对其限制条件进行了修改, 并且在脉冲项都含有一阶导数的情形下运用Leray-Schauder不动点定理探讨了该类问题解的存在性. 对非线性项和脉冲项做了一些假设, 证明了方程的解集有一个不依赖于参数λ的先验界, 进而得到结论: 方程至少有一个解. 最后通过一个实例说明了结论的应用.
脉冲微分方程; Leray-Schauder不动点定理; 多点边值问题
0 引 言
微分方程边值问题是一个具有持久生命力的课题. 近年来, 随着微分方程理论的发展, 多点边值问题的研究日益活跃[1-12], 特别是对于含有脉冲项的微分方程的多点边值问题的可解性得到了广泛的关注[8-17]. 但是, 对于非线性项、 脉冲项都含有一阶导数的多点边值问题的解的存在性的研究却不多见[11-14].
文献[1]利用五泛函不动点定理讨论了如下m点边值问题多个正解的存在性:
其中,ki>0(i=1,2,…,m-2),0<ξ1<ξ2<…<ξm-2<1.
对于脉冲微分方程, 文献[9]研究了含有导数脉冲的三点边值问题:
其中,f∈C(J×R2,R),Ik∈C(R,R),Jk∈C(R×R,R),T∈R,Z∈(0,1), 0 受文献[1,8]的启发,本文讨论了如下的二阶脉冲微分方程的m-点边值问题(BVP): 文中对文献[8]所研究的方程的脉冲项和边界条件做了推广, 对其限制条件进行了修改, 并且在脉冲项都含有一阶导数的情形下运用Leray-Schauder不动点定理获得了该类问题解的存在性定理. 引入以下空间: 引理 1[18]集合H⊂PC1(J,R)是相对紧集的充分必要条件为H中的诸函数x(t)及其导函数x′(t)都在J上一致有界且在每个Jk(k=1,2,…,m)上等度连续. 引理 2 若x∈PC1(J,R)∩C2(J′,R) 是BVP(1) 的解, 当且仅当x∈PC1(J,R)是下面的脉冲积分方程的解. 式中:x′(0)由式(6)给出. 证明 设x是BVP(1)的解, 对式(1)两端积分, 得 对式(4)再次积分, 得 x(t)= 在式(4)中分别令t=1,t=ξi, 有 结合边界条件, 有 即 因此, 由式(4), 式(6)可得式(2). 反过来, 假定x∈PC1[J,R] 是脉冲微分方程(2)的解, 易知x(0)=0, △x|t=tk=Ik(x(tk)). 当t≠tk时, 直接对式(2)求导, 可得 对式(7)两边再求导, 得 [-x″(t)=f(s,x(s),x′(s)),t≠tk, 定义算子A:PC1[J,R]→PC1[J,R]时, 由引理1和引理2容易验证, 算子A是从PC1(J,R)到PC1(J,R)的全连续算子. 引理 3[18](Leray-Schauder定理) 设X为实Banach空间, 算子A∶X→X为全连续算子, 若集合{‖x‖|x∈X,x=λAx,0<λ<1}是有界的, 则方程x=Ax至少有一个解. 定理 1 假设H1)和H2)及下列条件成立: C1) 存在有界函数α(t),β(t),γ(t), 使得 |f(t,x,y)|≤α(t)‖x‖+β(t)‖y‖+γ(t). C2) 存在非负常数nk,mk,lk, 使得 C3) 存在常数ak> 0, 使得 k=1,2,…,n. 那么BVP(1.1) 至少有一个解. 证明 由引理3可知, 只需要证明方程 的解集在PC1(J,R)∩C2(J′)中有一个不依赖于λ∈(0,1)的先验界. 可得 则 由此可知, 只需验证‖x′‖有界即可. 为了方便, 令x(t)=λ[x0(t)+I0(t)], 其中 当0≤t≤ξ1时, 当ξr-1≤t≤ξr,2≤r≤m-2时, 当ξm-2≤t≤1时, 由以上结论可知, 当0≤t≤1,ξr-1≤s≤min{ξr,t}时, x0(t)= 当0≤t≤1,max{ξr-1,t}≤s≤ξr时, 综上可知, 当ξr-1≤s≤min{ξr,t}时, 由H1)可得, 当max{ξr-1,t}≤s≤ξr时, 同理, 由H1)可得, 又因为 故对∀t,s∈[0,1], 即 由C3)知, 存在Nk>0, k=1,2,…,n, 有 ∀t∈J, ‖x‖+‖y‖≥Nk. 从而 ∀x,y∈(R×R). 其中 所以, 结合条件C1), 可得 ‖x′‖≤ 记 由以上分析, 可得对于∀0<λ<1, 都有 因此, ‖x′‖有界, 从而‖x‖也有界. 由引理3, 故BVP(1)至少有一个解.定理得证. 考察如下二阶脉冲微分方程 易验证BVP(9)满足定理1的所有条件, 因此BVP(9)至少存在一个解. [1]JiangWeihua,GuoYanping.Multiplepositivesolutionsforsecond-orderm-pointboundaryvalueproblems[J].J.Math.Anal.Appl., 2007(327): 415-424. [2]ZhangGuowei,SunJingxian.Positivesolutionsofm-pointboundaryvalueproblems[J].J.Math.Anal.Appl., 2004(291): 406-418. [3]LiuXiujun,QiuJiqing,GuoYanping.Threepositivesolutionsforsecond-orderm-pointboundaryvalueproblems[J].AppliedMathematicsandComputation, 2004(156): 733-742. [4]陆心怡, 张兴秋, 王林. 一类分数阶微分方程m点边值问题正解的存在性[J].系统科学与数学, 2014, 34(2): 218-230.LuXinyi,ZhangXingqiu,WangLin.Existenceofpositivesolutionsforaclassoffractionaldifferentialequationswithm-pointboundaryvalueconditions[J].JournalofSystemsScienceandMathematicalSciences, 2014, 34(2): 218-230. (inChinese) [5]JiangWeihua.Theexistenceofpositivesolutionsforsecond-ordermulti-pointBVPswiththefirstderivative[J].Comput.Math.Appl., 2009(225): 387-392. [6]许洁, 赵微. 一类三阶常微分方程m点边值问题的正解存在性[J]. 数学的实践与认识, 2013, 43(20): 255-260.XuJie,ZhaoWei.Theexistenceofpositivesolutionsofm-pointboundaryvalueproblemsforonekindofthird-orderordinarydifferentialequations[J].MathematicsinPracticeandTheory, 2013,43(20): 255-260. (inChinese) [7]ZhangXuemei,FengMeiqiang,GeWeigao.Multiplepositivesolutionsforaclassofm-pointboundaryvalueproblems[J].Appl.Math.Let., 2009(22): 12-18. [8]SunYing,ZhuDeming.Existencetheoremsforasecondorderthree-pointboundaryvalueproblemwithimpulses[J].Appl.Math.J.ChineseUniv.Ser.B., 2005, 20(2): 165-174. [9]LiuBing,YuJianshe.Existenceofsolutionform-pointboundaryvalueproblemsofsecond-orderdifferentialsystemswithimpulses[J].Appl.Math.Comput., 2002(125): 155-175. [10]TianYan,JiangDaqing,GeWeigao.Multiplepositivesolutionsofperiodicboundaryvalueproblemsforsecondorderimpulsivedifferentialequations[J].Appl.Math.Comput., 2008(200): 123-132. [11]张学梅, 葛渭高. 奇异脉冲微分方程m点边值问题多个正解的存在性 [J]. 北京理工大学学报, 2009(12): 1122-1125.ZhangXuemei,GeWeigao.Existenceofmultiplepositivesolutionstom-pointboundaryvalueproblemsforsingularimpulsivedifferentialequations[J].TransactionsofBeijingInstituteofTechnology, 2009(12): 1122-1125. (inChinese) [12]田景霞. 无穷区间上二阶脉冲微分方程多点边值问题的正解[J]. 应用泛函分析学报, 2012(14): 315-320.TianJingxia.Positivesolutionsofmultiplepointboundaryvalueproblemsforsecond-orderimpulsivedifferentialequations[J].ActaAnalysisFunctionalisApplicata, 2012(14): 315-320. (inChinese) [13]FengMeiqiang,XieDongxiu.Multiplepositivesolutionsofmulti-pointboundaryvalueproblemforsecond-orderimpulsivedifferentialequations[J].J.Comput.Appl.Math., 2009(223): 438-448. [14]YaoMeiping,ZhaoAimin,YanJurang.Anti-periodicboundaryvalueproblemsofsecondorderimpulsivedifferentialequations[J].Comput.Math.Appl., 2010(59): 3617-3629. [15]YaoMeiping,ZhaoAimin,YanJurang.Periodicboundaryvalueproblemsofsecond-orderimpulsivedifferentialequations[J].NonlinearAnalysis, 2009(70): 262-273. [16]ZhangLingling,ZhaiChengbo.Existenceanduniquenessofpositivesolutionstononlinearsecondorderimpulsivedifferentialequationswithconcaveorconvexnonlinearities[J] .DiscreteDyn.Nat.Society, 2013, 259730: 1-11. [17]JiangWeihua,ZhangQiang,GuoWeiwei.Multiplepositivesolutionsforsecondorderimpulsivedifferentialequation[J].Electron.J.Qual.TheoryDiff.Equa., 2013(6): 1-11. [18]郭大均. 非线性泛函分析[M]. 济南: 山东科技出版社, 2001. 声 明 本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中,以数字化方式复制、汇编、发行、信息网络传播本刊全文。该社著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我编辑部上述声明。 Boundary Value Problems for Second Order Multi-Point Difference Equations with Impulses LI Hai-yan1, GUO Yu-heng2, LI Li-mei3 (1. Dept. of Mathematics, Jincheng College of Sichuan University, Chengdu 611731, China; 2. University of Electronic Science and Technology of China, Chengdu 611731, China; 3. College of Math and Software Science, Sichuan Normal University, Chengdu 610068, China) The existence of solutions for multi-point boundary value problem of second-order impulsive differential equations was investigated. The boundary value conditions and impulsive term were extended. In the case of the impulsive term with the first derivative, the new conclusions about the existence of the solution are obtained via Leray-Schauder fixed-point theorem. It is proved that when the nonlinear term and impulsive term with some assumptions, a priori bounds for the solutions set of the differential equation doesn't depend on the parametersλ. It draws the conclusion that the differential equation has one solution at least. At last, the material example shows the application of the results. impulsive differential equation; Leray-Schauder fixed point theorem; multi-point boundary value problem 1673-3193(2017)04-0425-08 2016-11-23 四川省教育厅青年基金资助项目(12ZB108) 李海艳(1983-), 女, 讲师, 硕士, 主要从事非线性泛函分析研究. O175.8 A 10.3969/j.issn.1673-3193.2017.04.006

1 主要引理及其证明


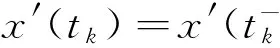


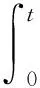
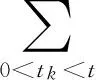

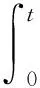

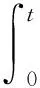
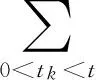
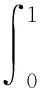


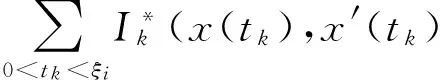
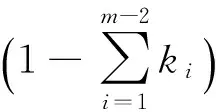









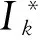
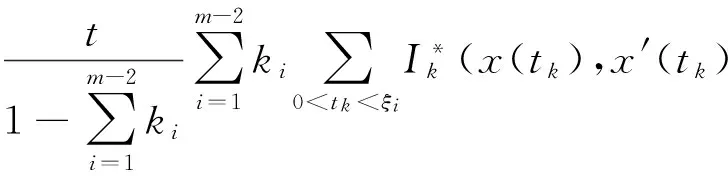
2 主要结论及证明
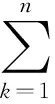
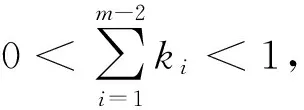



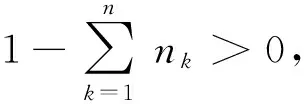



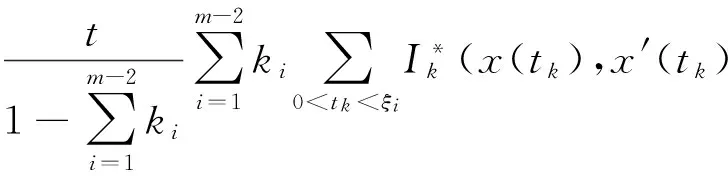
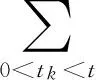



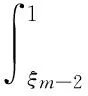

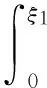
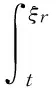
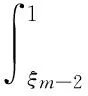

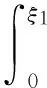
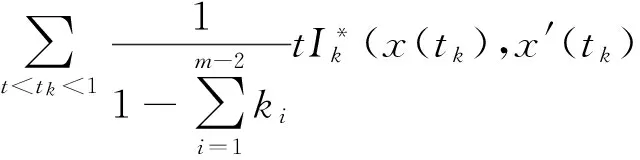

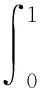
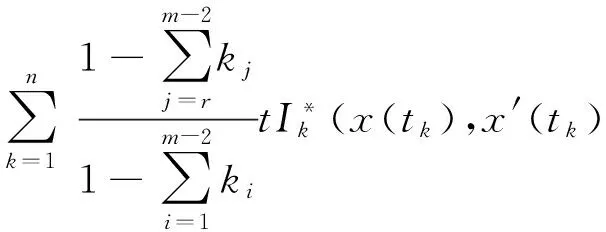

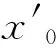
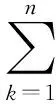

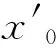
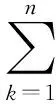
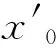
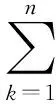

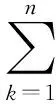

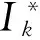


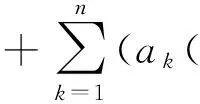

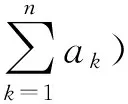

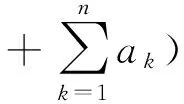


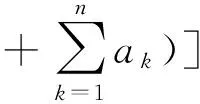






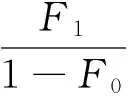
3 应用举例

