绝对差值排序的全变分低剂量CT重建算法
张鹏程, 张 权, 郝慧艳, 陈 燕, 桂志国,2
(1. 中北大学 电子测试技术国家重点实验室, 山西 太原 030051; 2. 中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051)
绝对差值排序的全变分低剂量CT重建算法
张鹏程1, 张 权1, 郝慧艳1, 陈 燕1, 桂志国1,2
(1. 中北大学 电子测试技术国家重点实验室, 山西 太原 030051; 2. 中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051)
针对传统全变分(Total Variation, TV)低剂量CT(Computed Tomography, CT)算法在重建图像时出现阶梯效应和模糊图像边缘的问题, 提出了基于绝对差值排序(Rank-Ordered Absolute Differences, ROAD)和中值先验(Median Prior, MP)模型的TV低剂量CT重建算法. 首先采用ROAD对传统TV模型中的扩散函数进行改进, 然后将改进后的TV模型与MP模型结合得到新的惩罚项, 最后将该惩罚项应用于基于惩罚加权最小二乘重建算法从而构造新的目标函数. 实验结果表明, 新算法不仅可以抑制阶梯伪影的产生, 还能够很好地保留图像边缘细节信息.
低剂量CT; 全变分; 阶梯效应; 中值先验; 绝对差值排序
计算机断层成像技术(Computed Tomography, CT)现已广泛应用于疾病预防、 临床诊疗等方面. 高辐射剂量会损害人体健康组织器官, 因此需要在降低辐射剂量的同时获取满足临床实际需求的解剖信息清晰、 密度分辨率高的CT图像. 辐射剂量的降低会导致从X射线源发出的光子数目急剧减少, 投影数据被噪声污染严重, CT图像中出现明显的条形伪影. 因此, 滤除低剂量CT图像中的噪声已成为众多学者研究的重点问题.
解决这一问题主要有3种方法: ① 对投影数据降噪处理反投影重建获取待求目标图像; ② 对低剂量CT含噪图像直接进行降噪的后处理算法; ③ 图象域统计迭代重建算法. 本文主要是针对低剂量CT的统计迭代重建算法进行研究. 针对加权最小二乘算法的不适定性, Wang等[1]采用逐次超松弛迭代算法[2]求解惩罚加权最小二乘(Penalized Weighted Least Square, PWLS)算法代价函数获得比较满意的图像效果, PWLS模型现已在低剂量CT图像的统计迭代重建算法中得到广泛应用. Zhang等[3]改进传统非局部均值先验模型中的滤波参数, 提出一种可以根据图像相似程度自动调节滤波强度的函数, 新算法在去除条形伪影的同时保留图像更多的边缘细节信息. 路利军等[4]通过利用解剖图像的区域信息进行自适应迭代估计来改进权值参数, 进而提出一种基于解剖自适应的非局部先验贝叶斯PET图像重建算法, 不仅对图像边缘有良好保持效果, 还能有效地提高病灶对比度. 王丽艳等[5]针对低剂量CT重建提出一种线性Bregrman迭代统计重建算法, 改善重建图像的质量且具有快的收敛速度. Sidky等[6]将全变分(TotalVariation, TV)最小化理论应用到锥束CT重建中, 并在视觉效果和定量分析方面都取得理想效果. 何琳等[7]提出一种自适应加权TV的低剂量CT统计迭代重建算法, 该算法中的边缘扩散函数基于图像的梯度和加权方差得到, 新函数可以对图像边缘细节邻域进行自动滤波处理, 因此, 重建图像边缘细小区域的噪声在得到有效抑制的同时没有模糊或牺牲细节特征.
TV最小化是目前最受欢迎的一种边缘保留的图像恢复方法. Tian等[8]将TV正则化先验模型引入到低剂量CT重建算法中, 获得的图像具有良好的边缘保持特性. TV正则化模型在去除图像噪声的同时会模糊图像的边缘, 使图像出现阶梯效应. Hsiao等[9]提出了一种具有优异的边缘保持能力的中值先验(Median Prior, MP)重建算法. 张芳等[10]提出一种基于小波和非局部的全变差MP重建算法, 在获得高质量图像的同时提高图像的抗噪声性能. Liu等[11]提出一种稀疏角度下的低剂量CT的MP约束的全变分算法, 可以得到高分辨率和高信噪比的CT重建图像. Shangguan等[12]提出一种联合正则的稀疏角度脑CT统计迭代图像重建, 通过MP和广义全变分来正则化传统PWLS的目标函数, 最终获得优质的高分辨率的脑CT图像. Garnett等[13]首次使用绝对差值排序检测法(Rank-Ordered Absolute Differences, ROAD)来去除图像噪声. 董婵婵等[14]将ROAD和小波收缩结合提出一种最大似然期望最大化的低剂量CT重建算法, 不仅可以抑制噪声, 还能较好地保持图像的边缘和细节信息. 受文献[9]和[13]的启发, 本文提出一种绝对差值排序的全变分低剂量CT重建算法, 首先使用可以区分图像光滑区域和边缘区域的ROAD改进扩散函数并将其运用到传统TV模型中, 然后将改进的TV模型与MP模型结合作为新的惩罚项, 再与PWLS重建算法构造出新目标函数. 通过视觉效果和量化指标分析, 新算法重建图像质量得到明显改善且边缘细节分辨率高.
1 投影数据噪声特性
图像噪声问题的实质就是一个随机过程的问题, 因此往往可以使用随机过程的概率分布函数和概率密度分布函数来描述噪声. 噪声按照统计学理论可分为两类: 一类是不随时间增长而变化的平稳噪声, 另一类是非平稳随机噪声, 其统计特性随时间而变. 如果依据噪声幅度分布的统计特性又可分为高斯噪声、 泊松噪声和瑞利噪声等. 高斯噪声服从正态分布且数学表达式简单易计算, 目前, 图像处理中常采用高斯噪声模型对理想图像进行噪声添加.
Wang[15]采用多层高速CT扫描机对仿真投影数据进行模拟实验, 通过计算投影数据的概率密度函数, 发现投影数据的噪声可以通过高斯分布进行准确的建模. Li等[16]得出低剂量CT投影近似地服从非平稳高斯分布, 其数学表达式为
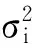
2 惩罚加权最小二乘重建算法
PWLS重建算法是在最小二乘估计(Least Squares, LS)算法中加入带有平滑约束的惩罚项得到. PWLS算法的目标函数为

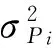
3 绝对差值排序的全变分低剂量CT统计迭代重建算法
3.1TV算法
TV算法是一种经典的图像去噪算法[6],TV的正则化模型为

3.2 中值先验
基于TV正则化约束的低剂量CT重建算法虽然取得很好的降噪效果, 但TV降噪算法往往会导致图像产生阶梯状伪影. 针对TV最小化先验存在的不足,Hsiao等[9]提出的MP先验在边缘保持能力方面表现优异, 因此本文惩罚项是由TV先验和MP先验共同决定.
MP可通过构造辅助向量得到, 其目标函数
φ
式中:m是f的辅助向量, 两者具有相同的维数;Nj是像素j的邻域;φ表示势能函数;fj和mk邻域像素间的相互关系用权值函数ωjk表示, 当k∈Nj时,ωjk的值为1, 当k∉Nj时,ωjk则为0.
势函数选取φ(z)=|z|, 则R(f,m)可改写为
|fj-mk|.
辅助向量邻域像素mk的大小为
mk=median{fj∶j∈Nk}.
3.3 绝对差值排序法
传统TV正则化算法, 对图像的平滑区域和边缘细节区域的滤波程度相同, 往往会造成平滑区域降噪不充分, 边缘区域滤波程度过强, 从而导致图像边缘模糊. 传统TV模型与MP的结合在一定程度上会抑制阶梯效应的产生, 但边缘细节依旧存在模糊不清的不足.
Garnett等[13]提出的ROAD可以有效地区分图像边缘和图像中含有的噪声, 因此, 将ROAD与偏微分方程中的扩散系数结合构成新边缘指示函数, 能够针对图像区域的不同而进行不同强度的去噪.ROAD的公式为
dx,y=|ux-uy|,
式中: 像素y表示以像素x为中心的邻域像素. 因此, ROAD是图像的一个局部统计特性, 本文是在3×3邻域中计算,dx,y是像素x和像素y的强度差的绝对值.
按升序排列dx,y的值, 则有
式中:ri(x)是第i小的dx,y; 2≤m≤7.
偏微分方程的扩散函数为
ct(x,y)=g(
图像边缘区域附近的邻域像素与中心像素的强度值相差较小,ROAD的值就较小, 滤波程度相对就小, 可以更好地保护图像的边缘区域; 图像中的噪声会使中心像素与周围大多数或所有邻域像素值相差很大, 表明ROAD的值较大, 边缘指示函数的值就越大, 就可以有效地去除图像中含有的大量噪声.
因此, 基于ROAD的新边缘指示函数可以表示为
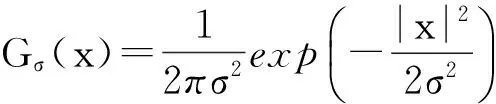
由上可知,ROAD可以很好地区分图像的边缘区域和噪声, 把ROAD引入到传统TV模型中是切实可行的, 可以有效地弥补传统TV正则化去噪算法模糊图像边缘, 产生阶梯效应的缺点.
3.4 绝对差值排序的全变分CT重建算法
基于ROAD的全变分模型表示为

绝对差值排序的全变分低剂量CT重建算法的目标函数可重写为
Φ(f)=(y-Gf)T∑-1(y-Gf)+
β1RMTV(u,f)+β2RMP(f,m).
采用可分离抛物面替代算法[17]求解式(12)为
采用梯度下降流和数值计算方法求解MTV模型, 则有

式中: ε是一个非常小的正参数, ε=10-8.
3.5 重建算法描述
算法描述如下:
1) 以FBP重建算法获取的重建图像作为初始化的CT重建图像, 记为f0;
2) 利用式(7)~(10)计算得到新边缘指示函数gROAD;
3) 将初始化图像f0和边缘指示函数函数gROAD代入式(13)~(15), 通过可分离抛物面法和梯度法求解新目标函数.
4) 重复2)和3)一定次数, 不断调整实验过程中涉及的所有参数, 选取高对比度、 高分辨率、 边缘清晰且与原图差距最小的图像作为所求图像.
4 实验结果与分析
采用Shepp-Logan大脑模型和数字胸腔模型[18]进行仿真实验来进一步验证本文所提算法的可行性、 有效性和可靠性. 算法的编程环境为MATLAB7.6.0(R2008a), 本文仿真实验是在操作系统为Windows7, 处理器为Intel(R)Core(TM)i7-4770KCPU@3.50GH, 内存为4G的计算机上进行. 图 1 展示的是Shepp-Logan大脑模型和数字胸腔模型, 两模型的尺寸均为256×256. 实验对比算法分别为惩罚加权最小二乘算法(PWLS)、 惩罚加权最小二乘全变分算法(PWLS-TV)、 惩罚加权最小二乘中指先验全变分算法(PWLS-MPTV).

图 1 实验模型Fig.1 Experimental model
同时, 采用式(1)中的非平稳高斯分布噪声模型向理想的投影数据中添加噪声, 其中ξi=200, η=22 000. 高斯滤波中的方差σ=15, 边缘指示函数中的扩散系数K=8, 控制保真项和惩罚项之间的平滑参数β1=8, β2=15.
图 2 给出的是大脑模型各算法恢复图像, 由图可知,PWLS算法获得的重建图像比较模糊, 不利于医生做出准确的诊疗判断.PWLS-TV算法在伪影抑制和噪声去除方面有明显提高, 由于TV只能逼近分片常数函数, 会出现阶跃响应, 表现在图像上就是阶梯效应, 恢复图像中引入了理想模型图像中没有的块状伪影.PWLS-MPTV算法能够去除PWLS-TV算法中的阶梯效应, 但由于该算法自适应能力较差, 会失去图像一小部分的特征结构. 本文算法几乎不会丢失图像的边缘细节纹理结构, 且重建图像清晰明亮、 分辨率高.
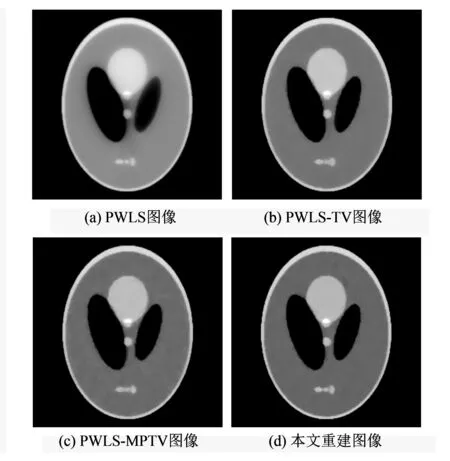
图 2 大脑模型各算法重建图像Fig.2 Reconstructed image processed by various algorithms for the brain model
为从视觉效果上更清晰明了地观察本文算法的优越性, 选取图2的4种算法重建图像的两个感兴趣区域(RegionofInterest,ROI)进行对比分析, 分别如图 3 和图 4 所示. 由图可知, 本文重建算法明显优于其他3种对比算法, 尤其在降噪能力、 伪影抑制、 边缘细节信息保留以及分辨率保持等方面表现优异.

图 3 图2各对比算法重建图像的ROI1放大图Fig.3 The ROI1 enlarged drawing of reconstructed image of Fig.2

图 4 图2各对比算法重建图像的ROI2放大图Fig.4 The ROI2 enlarged drawing of reconstructed image of Fig.2
为更直观地验证本文算法的优越性和有效性, 给出Shepp-Logan模型与4种算法重建图像在第125列的纵向剖面图的密度曲线, 如图 5 所示.PWLS算法与原始图像125列像素差异比较大,PWLS-TV算法与理想图像的差距减少但像素曲线波动较大不平稳. 本文算法不仅相比PWLS-MPTV算法更接近原图且波动最小, 表明本文所提算法有优异的边缘保持效果.

图 5 原图和各重建图第125列纵向剖面图Fig.5 Comparison of 125th column longitudinal profiles of reconstructed image processed by various algorithms
为保证本文所提算法更具普遍性, 接着采用数字胸腔模型做进一步深入的研究, 本文算法与3种对比算法的恢复图像分别如图 6 所示.PWLS算法虽在一定程度能抑制伪影和噪声, 但图像边缘模糊达不到理想的复原效果.PWLS-TV算法可以克服PWLS算法模糊图像的问题, 但却引入新的块状伪影.PWLS-MPTV算法在去除噪声方面有较大改善, 而且不会带来图像中未出现的伪影和噪声, 但该算法自适应能力不足, 会造成图像边缘细节纹理的损失. 本文算法在抑制大量噪声伪影的同时几乎不会过滤图像重要细节信息.

图 6 胸腔模型各算法重建图像Fig.6 Reconstructed image processed by various algorithms for the thoracic model
图 7 是图 6 中4种重建图像的局部放大图, 可以看出,PWLS算法复原图中残留噪声和伪影;PWLS-TV算法与PWLS算法相比, 滤除噪声和抑制伪影的能力有明显提高, 但代价是胸腔模型的局部区域出现块状伪影;PWLS-MPTV算法基本上可以满足临床应用需求, 但在滤除噪声的同时会过滤图像的边缘特征. 本文算法在去除噪声和边缘保留方面明显优于其他算法, 所得图像质量效果最佳.
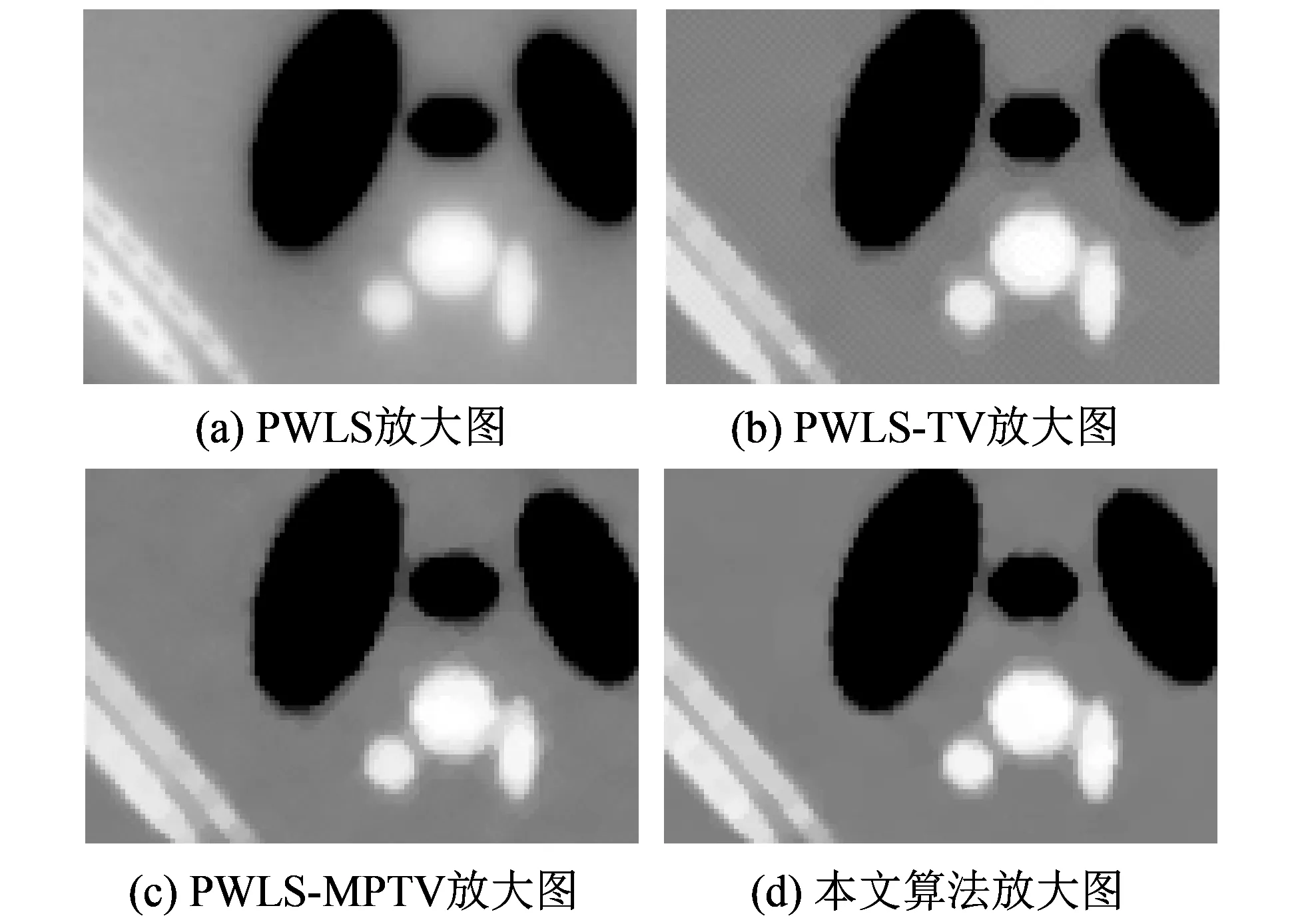
图 7 胸腔模型各算法局部放大图Fig.7 The local enlarged drawing of reconstructed image for the thoracic model
为定量评价本文算法的优越性, 则通过计算各重建图像与原图定量误差参数来评判重建效果的优劣性. 因此, 采用归一化平均绝对距离(NormalAverageAbsoluteDistance,NAAD)、 归一化均方距离(NormalizedMeanSquareDistance,NMSD)和信噪比(SignalNoiseRate,SNR)以及重建时间等定量评价指标, 其定义分别为
式中: M和N表示图像的行和列; Fi和qi表示重建图像与原图的像素灰度值; Mi和mi表示恢复图像与理想图像的均值. NAAD和NMSD的值表征重建图像与原始图像的差异程度, 其值越小表明越接近理想图像且算法复原效果佳. 信噪比SNR的值越大, 则反映图像失真程度越小, 重建图像质量越好.
表 1 和表 2 分别是Shepp-Logan模型和胸腔模型的各重建算法客观质量评价参数. 由表 1, 表 2 分析可知, 本文算法NMSD和NAAD值最小且有最高的SNR, 表明本文算法与原图差异最小, 信噪比高说明有用信息与噪声比值大, 可以重建出优质的图像.

表 1 大脑模型各算法质量评价参数
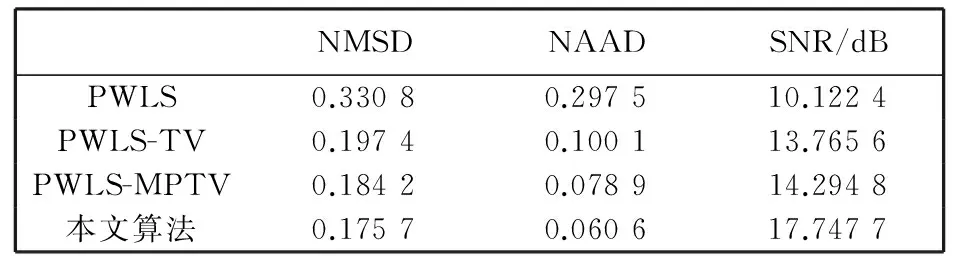
表 2 胸腔模型各算法质量评价参数
5 结束语
本文提出一种绝对差值排序的全变分低剂量CT重建算法, 首先采用基于ROAD的边缘指示函数改进传统TV模型, 接着将修改的TV模型、 MP模型和PWLS重建算法结合, 通过可分离抛物面法求解得到重建图像. 采用大脑和数字胸腔模型进行仿真实验, 主要从视觉效果(重建图像、 图像的ROI以及局部放大区域)、 像素曲线对比图以及定量评价参数等方面评估了算法的优越性.
[1]Wang J, Li T F, Lu H B, et al. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography[J]. IEEE Transactions on Medical Imaging, 2006, 25(10): 1272-1283.
[2]Fessler J A. Penalized weighted least-squares image reconstruction for positron emission tomography[J]. IEEE Transactions on Medical Imaging, 1994, 13(2): 290-300.
[3]Zhang Hao, Ma Jianhua, WANG Jing, et al. Statistical image reconstruction for low-dose CT using nonlocal means-based regularization. Part II: An adaptive approach[J]. Computerized Medical Imaging and Graphics, 2015, 43: 26-35.
[4] 路利军, 马建华, 黄静, 等. 基于解剖自适应的非局部先验贝叶斯PET图像重建[J]. 中国生物医学工程学报, 2011, 30(3): 326-332. Lu Lijun, Ma Jianhua, Huang Jing, et al. Bayesian PET image reconstruction with an anatomically adaptive nonlocal prior[J]. Chinese Journal of Biomedical Engineering, 2011, 30(3): 326-332. (in Chinese)
[5]王丽艳, 韦志辉.低剂量CT的线性Bregman迭代重建算法[J]. 电子与信息学报, 2013, 35(10): 2418-2424. Wang Liyan, Wei Zhihui. Linearized bregman iterations for low-dose CT reconstruction[J]. Journal of Electronics & Information Technology, 2013, 35(10): 2418-2424. (in Chinese)
[6]Sidky E Y, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine and Biology, 2008, 53: 4777-4807.
[7]何琳, 张权, 上官宏, 等. 自适应加权全变分的低剂量CT统计迭代算法[J]. 计算机应用, 2016, 36(10): 2916-2921. He Lin, Zhang Quan, Shangguan Hong, et al. Statistical iterative algorithm based on adaptive weighted total variation for low-dose CT[J]. Journal of Computer Applications, 2016, 36(10): 2916-2921. (in Chinese)
[8]Tian Z, Jia X, Yuan K H, et al. Low-dose CT reconstruction via edge-preserving total variation regularization[J]. Physics in Medicine and Biology, 2011, 56(18): 5949-5967.
[9]Hsiao I T, Rangarajan A, Gindi G. A new convex edge-preserving median prior with applications to tomography[J]. IEEE Transactions on Medical Imaging, 2003, 22(5): 580-585.
[10]张芳, 张权, 崔学英, 等. 基于小波和非局部的全变差中值先验重建算法[J]. 计算机工程与设计, 2015, 36(8): 2152-2156. Zhang Fang, Zhang Quan, Cui Xueying, et al. Total variation median prior reconstruction algorithm based on wavelet and nonlocal[J]. Computer Engineering and Design, 2015, 36(8): 2152-2156. (in Chinese)
[11]Liu Yi, Shangguan Hong, Zhang Quan, et al. Median prior constrained TV algorithm for sparse view low-dose CT reconstruction[J]. Computers in Biology and Medicine, 2015, 60: 117-131.
[12]Shangguan Hong, Liu Yi, Cui Xueing, et al. Sparse-view statistical iterative head CT image reconstruction via joint regularization[J]. International Journal of Imaging Systems and Technology, 2016, 26(1): 3-14.
[13]Garnett Roman, Huegerich Timothy, Chui Charles, et al. A universal noise removal algorithm with an impulse detector[J]. IEEE Transactions on Image Processing, 2005, 14(11): 1747-1754.
[14]董婵婵, 桂志国, 张权, 等. 基于ROAD和小波收缩的MLEM低剂量CT重建算法[J]. 计算机应用与软件, 2016, 33(2): 156-160, 178. Dong Chanchan, Gui Zhiguo, Zhang Quan, et al. MLEM low-dose CT reconstruction algorithm based on ROAD and wavelet shrinkage[J]. Computer Applications and Software, 2016, 33(2): 156-160, 178. (in Chinese)
[15]Wang Jing. Noise Reduction for low-dose X-ray computed tomography[D]. New York: Stony Brook University, 2006.
[16]Li T F, Li X, Wang J, et al. Nonlinear sinogram smoothing for low-dose X-ray CT[J]. IEEE Transactions on Nuclear Science, 2004, 51(5): 2505-2513.
[17]ElbakriiI, Fessler J. Statistical image reconstruction for polyenergetic X-ray computed tomography[J]. IEEE Transactions on Medical Imaging, 2002, 21: 89-99.
[18]Zhang Y K, Zhang J Y, Lu H B. Statistical sinogram smoothing for low-dose CT with segmentation based adaptive filtering[J]. IEEE Transactions on Nuclear Science, 2010, 57(5): 2587-2598.
Total Variation Algorithm Based on Rank-Ordered Absolute Differences for Low-lose CT Reconstruction
ZHANG Peng-cheng1, ZHANG Quan1, HAO Hui-yan1, CHEN Yan1, GUI Zhi-guo1,2
(1. National Key Laboratory for Electronic Measurement Technology, North University of China, Taiyuan 030051, China; 2. Key Laboratory of Instrumentation Science & Dynamic Measurement, North University of China, Taiyuan 030051, China)
A new total variation algorithm based on the rank-ordered absolute differences (ROAD) method and the median prior (MP) model for low-lose CT reconstruction was proposed to overcome the drawback of the traditional total variation (TV) algorithm, which can result in the staircase effect and blur the image edge for the low-dose computed tomography (CT). The ROAD was applied to improve the diffusion function of the traditional TV model at first. Then, combining with this TV model, a new penalty item was formulated with the improved MP model. At last, this new item was applied to establish the new objective function based on the penalized weighted least square reconstruction algorithm. The experiment results illustrate that the new algorithm can reducing staircase artifacts, while can well preserve image details and edges.
low-dose computed tomography; total variation; staircase effect; median prior; rank-ordered absolute differences
1673-3193(2017)04-0498-07
2017-02-27
国家自然科学基金资助项目(61271357); 山西省自然科学基金资助项目(2015011046); 中北大学2013年校科学基金资助项目
张鹏程(1984-), 男, 讲师, 博士, 主要从事图像处理与重建, 剂量计算与方案优化的研究.
TP391
A
10.3969/j.issn.1673-3193.2017.04.017

