强制性与半强制性减速带效用模型拟合及验证
林培群,雷永巍,顾玉牧
(华南理工大学 土木与交通学院,广东 广州 510640)
强制性与半强制性减速带效用模型拟合及验证
林培群,雷永巍,顾玉牧
(华南理工大学 土木与交通学院,广东 广州 510640)
观测并定量分析了车辆通过强制性减速带与半强制性减速带的速度;建立了双车道橡胶减速带速度与距离二次多项式模型,及双向八车道半强制性减速带速度与距离指数型函数模型,描述了速度控制设施的减速效用;并对模型的可靠性和有效性进行了验证。结果表明:研究的强制性和半强制性减速带均适合于同等路况及同类型减速带设置的情况。
交通工程;强制性减速带;半强制性减速带;效用模型;模型拟合
0 引 言
目前,强制性与半强制性减速设施正被广泛使用于各种场合[1-2],其种类主要有热塑振动标线、减速丘、路面凹形槽减速带、道钉减速带和驼峰式橡胶减速带等,在实际应用中都取得了一定的效果[3]。国内外学者主要集中于对减速带尺寸及对车辆通过减速带时引起的振动问题两方面进行研究。邱望标等[4]通过研究减速带形状对车辆振动的影响,得出了最为理想的减速带形状是抛物线;B.J.KATZ等[5]通过仿真实验,得出了视错觉减速标线能够有效地降低车辆行驶速度的结论;E.KHORSHID等[6]对车辆通过减速带时振动特性进行了分析并建立了模型;侯臣元等[7]建立汽车通过减速带的振动模型,对车辆进行模型简化,找出了车速和减速带截面尺寸与最大振动加速度之间的关系。
目前我国针对减速设施设置的具体理论研究还比较缺乏,为了更好地了解各种速度控制设施在实际应用中的效果,笔者针对我国半强制性减速带和强制性减速带的速度控制效用进行定量分析。选取山东省威海市城区设置的强制性减速带和半强制性减速带进行实地调查、采集数据,并建立拟合模型深入分析减速带的控速效用。技术路线如图1。
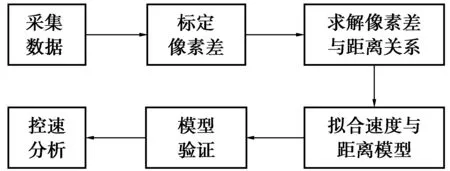
图1 技术路线Fig. 1 Technology road map
1 实证地点选择及数据采集
1.1 采集地点的确定
笔者选择半强制性减速带和强制性减速带分别进行研究。半强制性减速带为横向振动减速标线,其表面的突起可使道路车辆产生轻微的振动,提醒驾驶员需减速行驶;强制性减速带为驼峰式橡胶减速带,主要由特殊橡胶制成,其截面多为圆弧状或梯形,具有较好的减震抗压性。
我国JT/T 713—2008《橡胶减速带标准》规定:橡胶减速带截面形状应近似梯形,表面应带有增大抗滑力的凹凸结构,地面宽度300~400 mm,高度30~60 mm。我国GB5768.3—2009《道路交通标志和标线 第三部分:道路交通标线》规定:车行道减速标线可以用振动标线形式。但标准中对振动减速标线的具体设置方式未作特殊规定。
笔者选择了威海市两处具有代表性的路段进行数据采集:①威海市仁泰花园路段上强制性减速带,双车道,两侧无非机动车道,橡胶减速带宽350mm,高40mm,如图2(a);②威海市文化西路路段上半强制性减速带,双向八车道,有中央分隔带,有非机动车道,如图2(b)。

图2 减速带示意Fig. 2 Speed humps schematic
1.2 采集指标及方法
1.2.1 采集指标
车辆运行状态的主要指标有速度、流量、密度、车头时距、车头间距和延误。为了研究减速装置对车辆运行状态的影响,选取了速度这一最能连续且直接反应车辆运行状态变化的指标[8]。采集数据时,为了排除极端条件对车速的影响,选取了道路通畅时车辆样本。路段通畅时道路上所行驶车辆的速度是比较相近的。
1.2.2 采集方法
传统人工量测法、录像法及雷达测速法这3种方法可获得车辆通过减速设施时完整的速度变化曲线。传统人工量测法测速得到的是在一段行驶距离的平均车速,与速度的实际变化情况相差很大;录像法需要在路面上做大量较小间隔的标记,将会对驾驶员造成视觉干扰,影响实验真实性;雷达测速法需要测量人员尽可能快地对车辆进行连续测速,方能得到连续的瞬时车速,在实践过程中由于人工操作容易导致精度下降[9]。
笔者基于改进的录像法,将测速问题转化为测距离与时间问题,解决了传统录像法需在路面上做大量标记且容易对驾驶员造成视觉干扰的问题。
在实验中,借用一个已知距离的实物,如图3的参照杆,可以测得参照杆在行进中与减速带的距离以及录像截取图片中上下两个参照点的像素差。
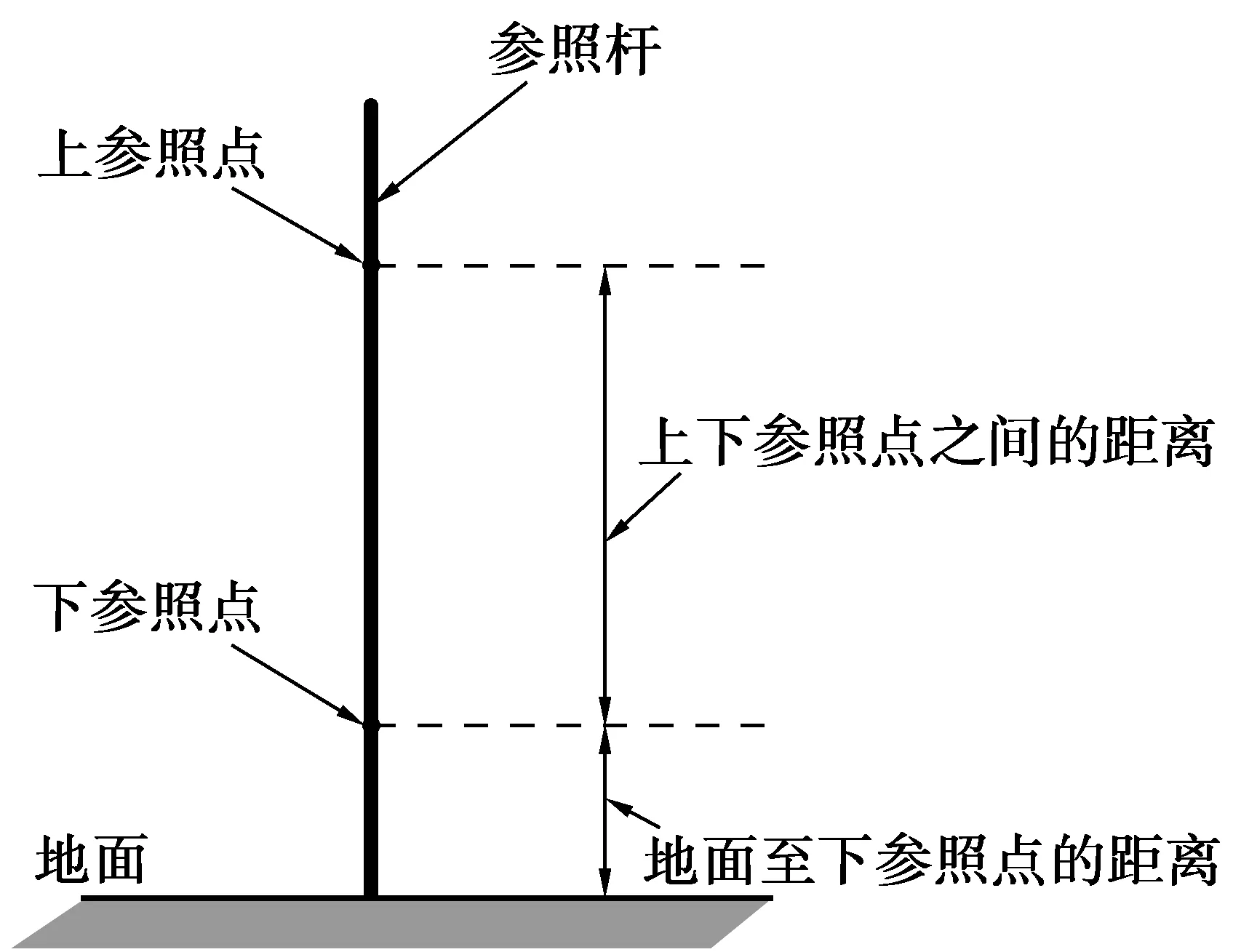
图3 参照杆示意Fig. 3 Referring rod schematic
利用测量参照杆到减速设施的距离值与参照杆对应点像素差之间的关系,获取录像截取的图片中标杆与车辆的共同高度像素差,得到函数关系,从而得出车辆到减速带的实际距离[10-12]。图4为目标比例变化示意。

图4 目标比例变化示意Fig. 4 Variation schematic of target ratio
录像中第k帧可以表示为
f(x,y,k)=M(x,y,k)+B(x,y,k)+n(x,y,k)
(1)
式中:M(x,y,k)为运动目标;B(x,y,k)为背景部分;n(x,y,k)为噪声部分。
同理,第k+1帧表示为
f(x,y,k+1)=M(x+Δx,y+Δy,k+1)+B(x,y,k+1)+n(x,y,k+1)
(2)
将式(1)与式(2)相减,得到相邻两帧图像的差分图像
Diff(x,y,k)=f(x,y,k+1)-f(x,y,k)=
[M(x+Δx,y+Δy,k+1)-M(x,y,k)]+[B(x,y,k+1)-B(x,y,k)]+[n(x,y,k+1)-n(x,y,k)]
(3)
式中:[M(x+Δx,y+Δy,k+1)-M(x,y,k)]为由目标运动而引起的图像变化区域;[B(x,y,k+1)-B(x,y,k)]为相邻帧间的背景差;[n(x,y,k+1)-n(x,y,k)]为相邻帧间残留的噪声。
1.2.3 具体方法
将两台摄像机设置于减速设施的两侧,分别拍摄车辆进入减速设施与驶离减速设施的情况,如图5。摄像机A距离减速带0.70 m,参照杆高1.30 m。
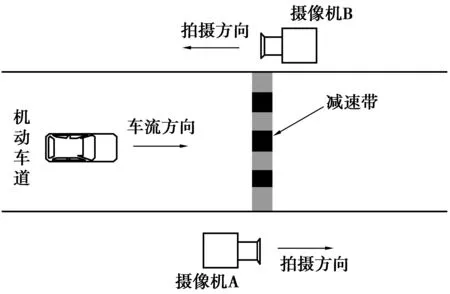
图5 减速带调查实验Fig. 5 Survey experiment of deceleration zone
2 模型拟合
2.1 强制性减速带效用模型拟合
在对摄像机A标定过程中,共标定了27段,由于直接读取像素差值较大,故采用1/10像素差作为参数进行运算。根据数据,得出1/10像素差与距离之间的关系,如图6。

图6 摄像机A参照杆1/10像素差与距离的关系Fig. 6 Relationship between the lever 1/10 pixel difference of camera A and distance
分析图6拟合趋势线,得到参照杆到摄像机位置的距离与其1/10像素差值的关系
y=29.417x-0.626
(4)
式中:x为参照杆1/10像素差值;y为参照杆与摄像机A的实际距离。
参照杆到摄像机位置的距离与其1/10像素差值的关系符合乘幂运算,相关系数R2=0.971 5,拟合效果较好。
同理,摄像机B与参照杆1/10像素差值之间距离关系
y=42.230x-0.635
(5)
相关系数为R2= 0.969 1,拟合效果较好。
2.2 强制性减速带对车辆运行影响效果
通过对摄像机中记录的车辆像素差组进行统计,将每组值代入式(4)、式(5)中,即可计算出车辆在通过减速设施过程中其与摄像机的相对位置。为了得到每辆车通过减速带过程中的速度值变化曲线(以2帧0.08 s计),只需将得到的距离变化值与行驶的时间做比值。
2.2.1 分析方法说明
由于行驶在被测路段的车型大多为小汽车,因此选择减速设施对小汽车的控速效果进行研究。定义车辆行驶方向为正方向,减速设施所在位置为0点,以0.5 m作为计数间隔,对在0.5 m间隔内的所有车速值求平均作为该点的速度值。并且由于摄像机距离减速设施还有0.7 m,所以在计算得到车辆与摄像机之间的距离后应减去0.7 m。
2.2.2 空间效果分析
选择离减速设施距离-12.0 ~ 6.5 m的路段作为分析对象,共获得了156个有效样本。数据处理后绘制距离与平均速度的关系如图7。
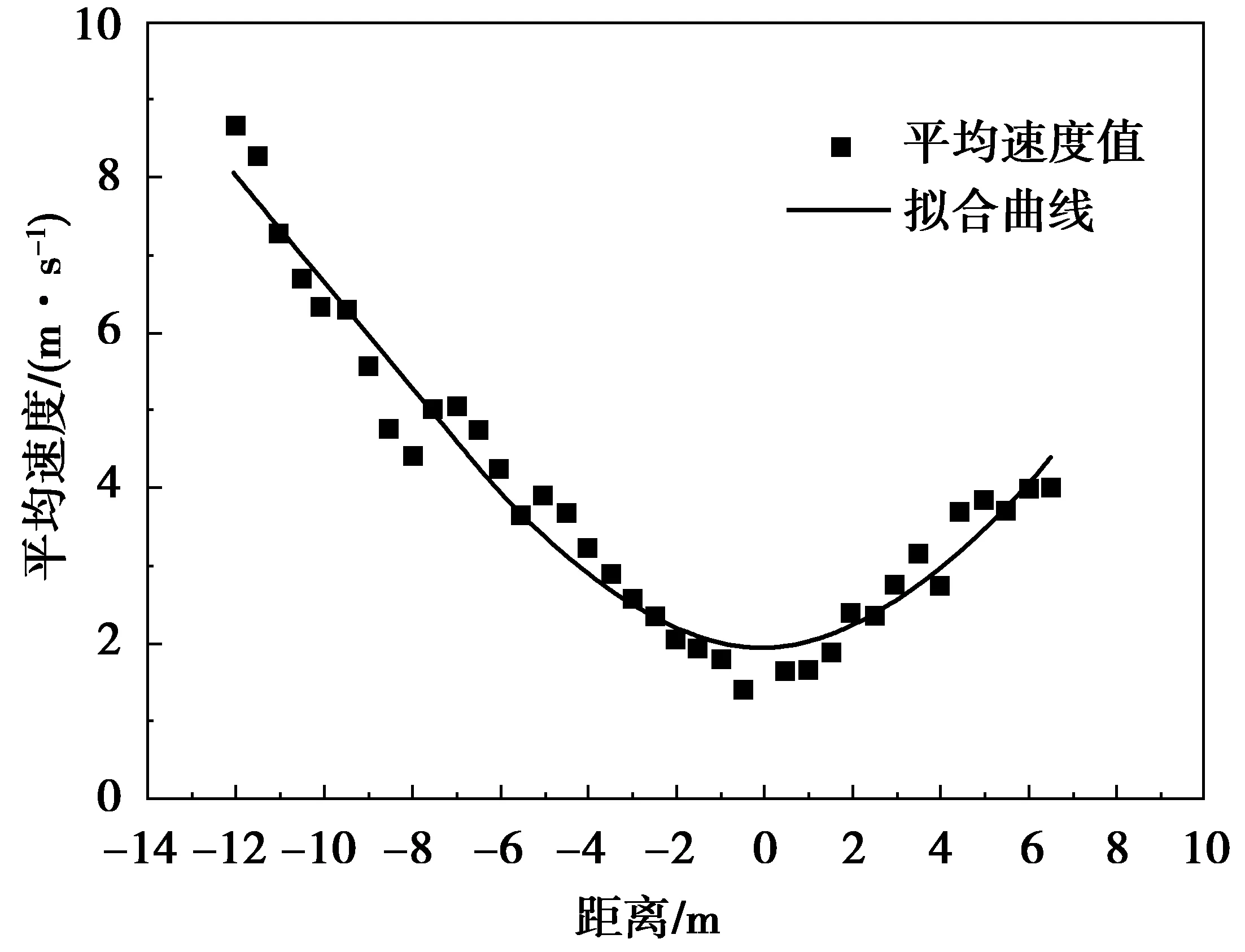
图7 强制性减速带效用拟合Fig. 7 Utility fitting of mandatory speed humps
从图7中可以看出:车辆自西向东方向行驶过程中,由于减速设施的存在,在距离减速设施-8 m处速度值有一个波动;此后车速继续下降,在距离减速设施还有0.5 m左右时速度最低;车辆通过减速设施之后速度呈较缓的趋势上升。
对图7进行拟合,获得车辆到减速带实际距离与速度之间的函数关系式
y=0.045 5x2+0.010 8x+2.181 9
(6)
s.t. -12.0≤x≤6.5
式中:x为车辆到减速带实际距离;y为车辆速度。
由式(6)可知,车辆到减速带实际距离与速度之间的关系符合多项式运算。运用SPSS软件进行拟合,分析得到相关系数R2= 0.951 9,说明拟和效果很好,可以使用这一模型进行数据分析。对所收集的数据进行统计分析得表1。
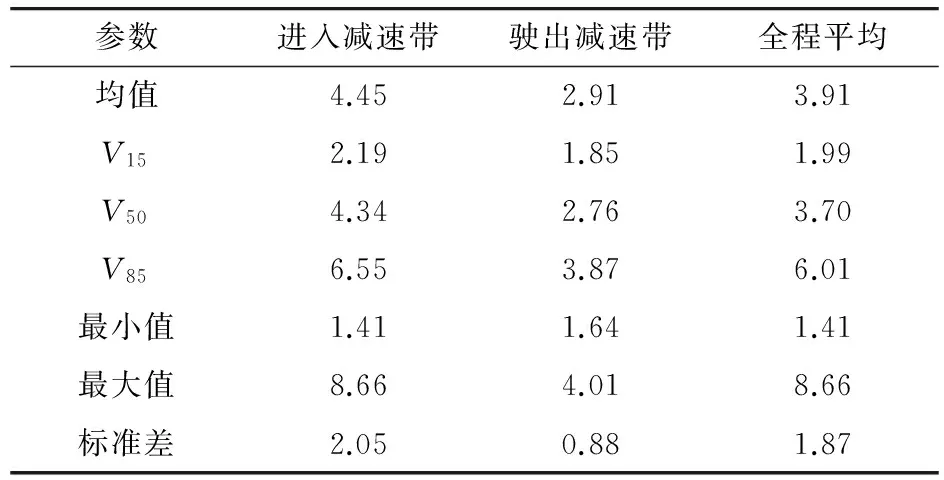
表1 强制性减速带车辆运行速度统计结果
注:V15为第15%位车速;V50为第50%位车速;V85为第85%位车速。(下同)
从表1可以看出,车辆到达减速带前速度变化较大,车辆运行速度最大为8.66 m/s,最小为1.41 m/s,减少了7.25 m/s。当车辆通过强制性减速带后速度开始提升,加速度值约为1.2 m/s2,整个过程速度变化呈现出先下降后回升的特点。
2.3 半强制性减速带效用模型拟合
同样的方法,可得到在半强制性减速带下1/10像素差与距离之间的关系,如图8。
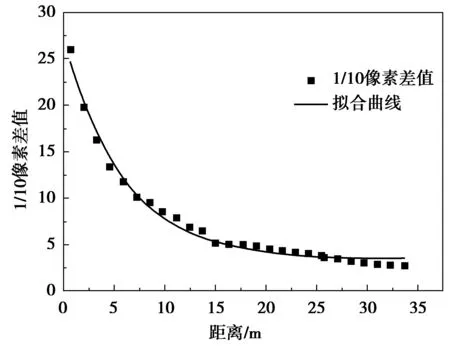
图8 摄像机A参照杆1/10像素差与距离的关系Fig. 8 Relationship between the lever 1/10 pixel difference of camera A and distance
分析图8拟合趋势线,得到参照杆到摄像机A位置的距离与其1/10像素差值的关系
y=32.041x-0.655
(7)
式中:x为参照杆像素差值的1/10;y为参照杆与摄像机A的实际距离。
参照杆到摄像机位置的距离与其1/10像素差值的关系符合乘幂运算,相关系数R2=0.950 3,拟和效果较好。
同理,得到摄像机B与参照杆1/10像素差与距离关系
y=39.784x-0.635
(8)
相关系数为R2=0.958 2,拟合效果较好。
2.4 半强制性减速带对车辆运行影响效果
选择距离减速带-14.5~9.5 m路段作为分析对象,共获得163个有效样本。绘制出距离与平均速度的关系,如图9。
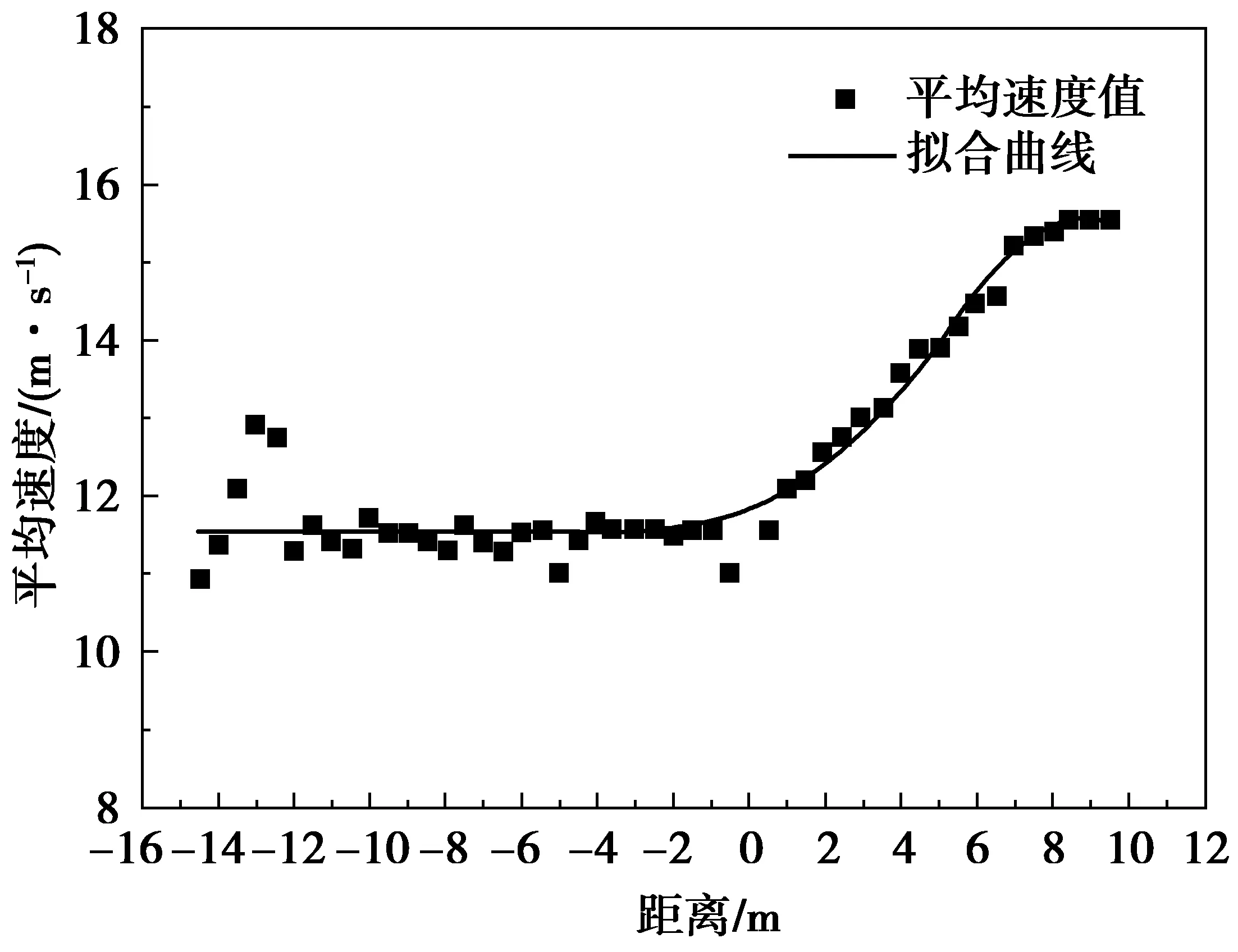
图9 半强制性减速带效用拟合 Fig. 9 Utility fitting of semi-mandatory speed humps
由图9可得:车辆自西向东方向行驶过程中,在距离减速带-13 m处有一个跳动,然后车速呈平稳趋势,在通过减速带前整体是匀速的;驶过减速带后车速呈较缓的趋势逐渐加速,在7 m附近达到速度的稳定值,此后又开始匀速行驶。
通过对图9进行拟合,获得车辆到减速带实际距离与速度之间的函数关系式
y=11.536+3.987e0.034(x-8.813)2
(9)
s.t. -14.5≤x≤9.5
式中:x为车辆到减速带实际距离;y为车辆速度。
由式(9)可知,车辆到减速带实际距离与速度之间的关系符合多项式运算。运用SPSS软件进行拟合,分析得到相关系数R2= 0.939 5,拟和效果较好,可以使用这一模型进行数据分析。
对所收集的数据进行统计分析得到表2。
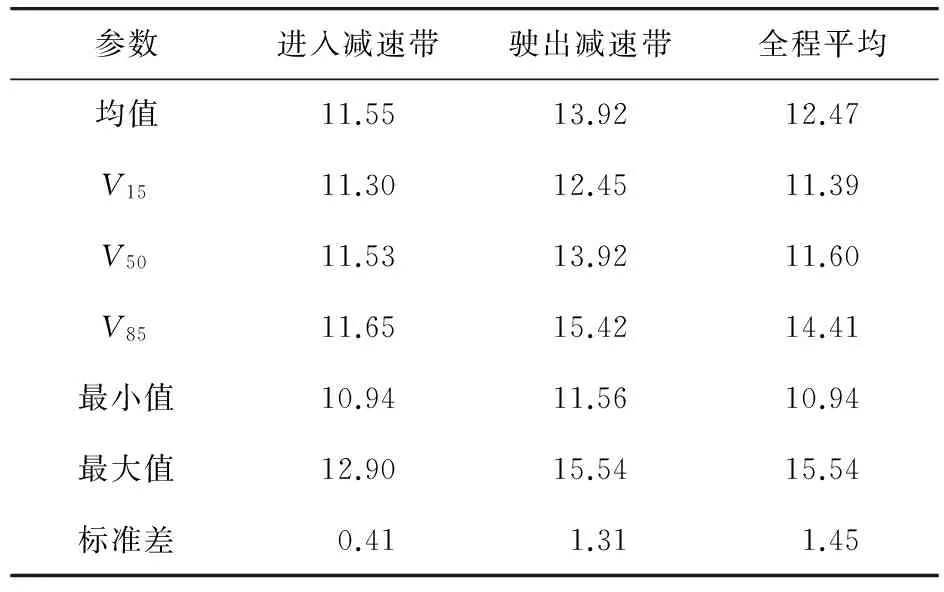
表2 半强制性减速带车辆运行速度统计表
从表2可以看出,车辆到达减速带前速度比较高,车辆的85%分位运行速度达到了11.65 m/s。当车辆的速度未超过路段限制速度时,经过3个连续的半强制性减数带,车辆的速度基本保持不变;当车辆通过减速带后,速度开始小幅度提升,在车辆达到一个接近限速值后,速度值保持稳定,整个过程速度值变化不大。
分析可知,车辆通过强制性减速带时,车速与距离符合二次多项式模型;通过半强制性减速带时车速与距离符合指数型函数模型。
3 模型验证与分析
3.1 模型验证
笔者采用雷达测速法进行地点速度的测量,并对测得的地点速度与用模型计算出的速度进行比较,从而对模型进行验证。
实验所用仪器为手持式雷达测速仪。速度测量选择在6个断面进行,断面设置位置如图10,图中,x为距减速带中心的距离,以车流方向为正。
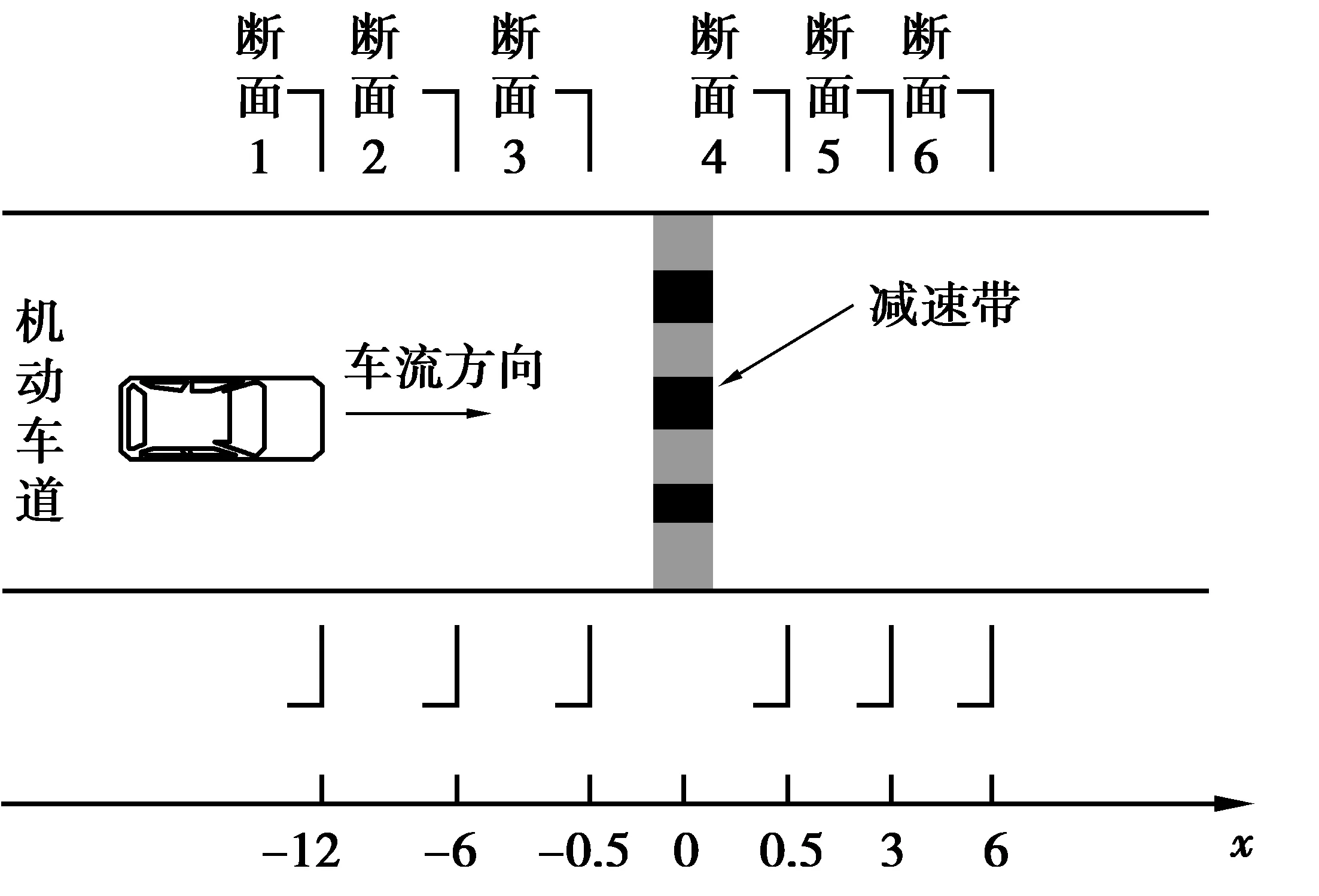
图10 速度观测断面示意(单位:m)Fig. 10 Schematic of speed observing section
同时,为了验证的合理性,采集数据的值分为2类:相同位置减速带速度值及同类型减速带值。本次调查得到的数据经过统计如图11。
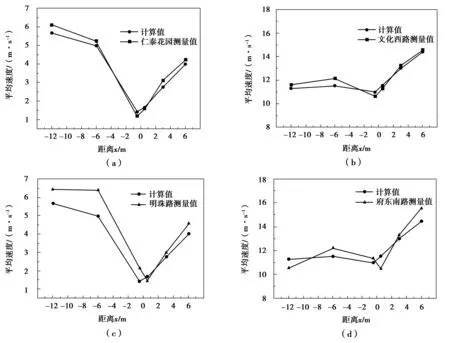
图11 强制性、半强制性减速带效用模型检验Fig. 11 Check of utility fitting model of mandatory and semi-mandatory speed humps
由图11(a)、(c)可见,计算值与测量值之间的差距较小。图11(a)中,检验的6个断面误差最小为0.03 m/s,最大为0.45 m/s;图11(c)中,检验的6个断面误差最小为0.08 m/s,最大为0.62 m/s。
由图11(b)、(d)可见,由于所在路段上的坡度、周围环境、交通量等不同而导致减速值不尽相同,但它们的减速趋势是相同的。
综上,可以得出文中所拟合出的强制性减速带模型比较合理,对于该类减数带设置具有一定的参考价值。
3.2 减速带效用对比分析
将2种不同类型的减速带对车辆速度的影响综合起来分析,根据数据建立图12。
由图12可以明显地发现,强制性减速带的减速效果最为明显,它使车辆在靠近减速带设置位置之前速度呈下降趋势,在到达设置位置时通常速度达到最小值,通过之后速度呈现出缓慢上升。半强制性减速带对车辆的影响很微弱,驾驶员在看清这类减速带时通常不会采取过多的减速,往往是保持速度行驶而过。
4 结 论
1)通过对录像法采集车辆数据进行改进,采集数据时避免了路面标记对驾驶员的影响,增加了数据的准确程度;建立了车辆通过强制性减速带和半强制性减速带时速度与距离关系的模型。同时通过雷达测速计采集同一位置和同种类型减速带的数据对建立的模型进行了有效验证,结果证明了模型的适用性。
2)对强制性减速设施和半强制性减速设施进行实地研究,分析了其减速效果。当车辆通过强制性减速带时速度会明显下降,通过半强制性减速带时速度基本稳定,单独依靠半强制性减速带是不能起到控制速度的作用。发现了1/10像素差与距离符合指数模型;车辆通过强制性减速带时车速与距离符合二次多项式模型,通过半强制性减速带时车速与距离符合指数型函数模型。
3)笔者拟合的强制性减速带和半强制性减速带模型可为今后在相同路况下设置减速带时提供参考,便于减速带设置人员对减速带安全性、实用性进行评估。
4)由于数据采集是在夏季进行,没有考虑雨雪雾等天气情况,研究具有一定季节局限性。恶劣天气状况下的情况需要进一步研究。
[1] 郭延永,刘攀,梁启宇.视觉减速标线控速效果评价[J].交通信息与安全,2014,32(6):106-112. GUO Yanyong, LIU Pan, LIANG Qiyu. Evaluation of the speed-control effects of illusionary pavement markings [J].JournalofTransportationInformationandSafety, 2014, 32(6):106-112.
[2] 胡斌,袁黎,吴文路.橡胶减速带几何设计优化研究[J].公路交通技术,2014,30(3):152-154. HU Bin, YUAN Li, WU Wenlu. Research on geometrically optimized design of rubber deceleration strips [J].TechnologyofHighwayandTransport, 2014, 30(3): 152-154.
[3] 陈瑜,杨秀峰,翟宁群,等.减速丘的速度控制效果研究[J].中外公路,2012,32(3):348-350. CHEN Yu, YANG Xiufeng, ZHAI Ningqun, et al. Study on speed control effect of reducing hill [J].JournalofChina&ForeignHighway, 2012, 32(3):348-350.
[4] 邱望标,黄克,黎熊,等.减速带形状对汽车振动的影响分析[J].橡胶工业,2008,55(11):657-659. QIU Wangbiao, HUANG Ke, LI Xiong, et al. Effect of the shape of decelerating belt on automobile vibration [J].ChinaRubberIndustry, 2008, 55(11):657-659.
[5] KATZ B J, DUKE D E. Design and evaluation of peripheral transverse bars to reduce vehicle speeds [C/OL] // Washington, D. C.:TransportationResearchBoard85thAnnualMeeting, 2006 [2015-08-12].http://xueshu.baidu.com/s?wd=paperuri%3A%285fa23e5d3c66c669c25050b81acb3eef%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Ftrid.trb.org%2Fview.aspx%3Fid%3D776411&ie=utf-8&sc_us=11409341028562483848.
[6] KHORSHID E, ALKALBY F, KAMAL H. Measurement of whole-body vibration exposure from speed control humps [J].JournalofSound&Vibration, 2007,304 (3/4/5):640-659.
[7] 侯臣元,彭为,靳晓雄,等.汽车通过减速带动力学响应分析[J].机械设计与研究,2010,26(2):95-98. HOU Chenyuan, PENG Wei, JIN Xiaoxiong, et al. Dynamic response analysis of vehicles passing over speed control humps [J].MachineDesignandResearch, 2010, 26(2): 95-98.
[8] 占劲松,闵强,汤乾斌.国省干线公路减速设施设置技术研究[J].公路与汽运,2015(1):73-77. ZHAN Jinsong, MIN Qiang, TANG Qianbin. Research on deceleration facilities in national and provincial roads [J].Highways&AutomotiveApplications, 2015(1): 73-77.
[9] 褚端峰,李浩然,张存保,等.振动减速带对行车安全的影响及控速效果分析[J].中国安全科学学报,2014,24(6):86-91. CHU Duanfeng, LI Haoran, ZHANG Cunbao, et al. Analysis of effects of vibrating deceleration bump on driving safety and its speed control effectiveness [J].ChinaSafetyScienceJournal, 2014, 24(6): 86-91.
[10] 毛育佼,陈苒君,唐莉萍.视频图像中运动目标检测算法的提高[J].计算机系统应用,2014,23(4):107-111. MAO Yujiao, CHEN Ranjun, TANG Liping. Optimization of the moving target detection algorithm in video images [J].ComputerSystems&Applications, 2014, 23(4): 107-111.
[11] 郑芳. 道路控速设施的设计及应用研究[D].长春:吉林大学,2008. ZHENG Fang.ResearchonDesignandApplicationofRoadSpeedControlFacilities[D]. Changchun: Jilin University, 2008.
[12] 孙毅刚,李鸿,张红颖.基于改进混合高斯模型的运动目标检测算法[J].计算机工程,2012,38(18):166-170. SUN Yigang, LI Hong, ZHANG Hongying. Moving object detection algorithm based on improved Gaussian mixture model [J].ComputerEngineering, 2012, 38(18): 166-170.
(责任编辑:田文玉)
Fitting and Verification of Utility Model of Mandatory and Semi-mandatory Speed Humps
LIN Peiqun, LEI Yongwei, GU Yumu
(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, P. R. China)
Observation and quantitative analysis on the vehicles’ speed decelerating by mandatory and semi-mandatory speed humps were carried out, and a quadratic polynomial model of dual carriageway rubber speed humps speed and distance was established. The exponential function model of two-way eight-lane semi-mandatory speed humps speed and distance was also established. The decelerating utility of speed control facilities was described. The reliability and validity of the proposed model were checked. Results show that the studied mandatory and semi-mandatory speed humps are suitable for the same type of roads and the same type of deceleration zone settings.
traffic engineering; mandatory speed humps; semi-mandatory speed humps; utility model; model fit
10.3969/j.issn.1674-0696.2017.07.19
2015-10-20;
2017-04-01
国家自然科学基金项目(61573149,61572233);广东省交通运输厅科技项目(2015-02-062);中央高校基本科研业务费资助项目(SCUT-2015ZZ008)
林培群(1980—),男,广东饶平人,教授,博士,主要从事车联网、智能交通方面的研究。E-mail: pqlin@scut.edu.cn。
U491
A
1674-0696(2017)07-111-06

