青藏高原双车道事故严重程度预测模型的建立

孙小端，侯洋洋，贺玉龙，冯丙丙

(北京工业大学 交通工程北京市重点实验室，北京 100124)



青藏高原双车道事故严重程度预测模型的建立

孙小端，侯洋洋，贺玉龙，冯丙丙

(北京工业大学 交通工程北京市重点实验室，北京 100124)

分析了青藏高原地区的交通事故数据，发现大部分交通事故都是死伤人数较高的事故，即死伤事故占比较大。将事故严重程度作为因变量，选取海拔、氧含量、天气、事故地点的线形、事故地点的环境、肇事车辆的类型、交通量、大车比例、大小车的速度差等9个因素作为自变量，建立了累积Logistic回归预测模型，研究了影响高原地区交通事故严重程度的因素。结果表明：海拔、大车比例、交通量、肇事车辆类型和大小车的速度差与交通事故严重程度有显著的相关性。预测模型的建立能够为相关公路管理部门制定安全措施提供理论依据。

交通工程；累积Logistic模型；青藏高原；事故严重程度预测

0 引 言

青藏高原地区因其特殊的地理位置、低压缺氧的气候、恶劣的自然条件、复杂的地质条件和脆弱的生态环境，使得道路行车安全性极差，极易发生重特大事故。高原地区人烟稀少，交通安全保障设施不足，导致发生交通事故后常常得不到及时的救援，造成人员伤亡，加剧交通事故的严重程度；高原无人区的部分路段线形差，路侧多山峰也易造成严重交通事故的发生；高原地区海拔高，驾驶员容易缺氧，易疲劳，也成为影响交通安全的重要因素。

近年来，我国交通安全形势比较严峻，突出表现为交通事故较严重。据2013年道路交通事故统计年报[1]，根据2009—2013年各省市一次性死亡10人以上的重、特大道路交通事故数据整理出东部地区、中部地区和西部地区的事故数及伤亡人数，发现西部地区无论事故数量还是伤亡人数均高于中、东部地区(图1)。

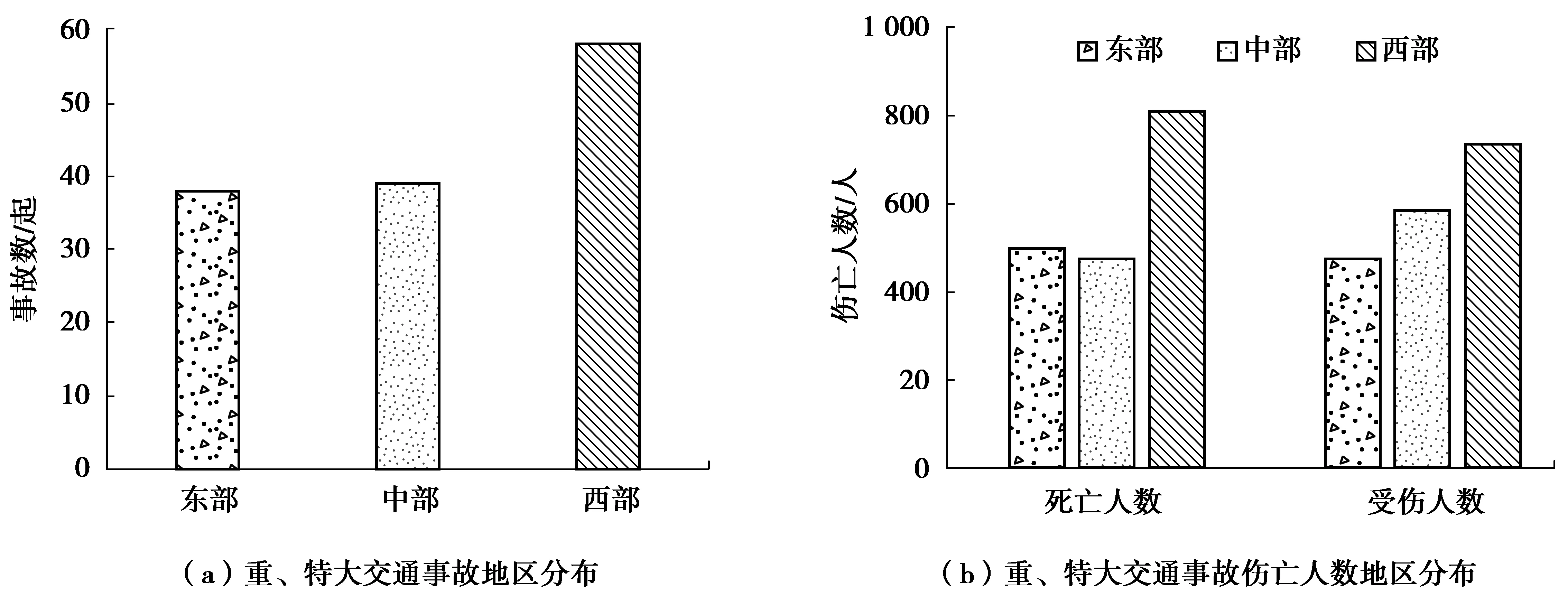
图1 2009—2013年一次死亡10人以上的重、特大交通故数及伤亡人数地区分布Fig. 1 The number of major traffic accidents with more than 10 people death and the area distribution of deaths/injuries in 2009-2013

国内外关于高海拔的公路交通安全预测模型的相关研究较少，多集中在非高原条件下的交通安全预测模型的研究。王谦等[2]通过对高原地区1 894起交通伤亡事故的分析，得出高原交通事故地点、事故车型、事故形态、事故原因等分布规律及特性。

在非高原条件下，常常采用Logistic回归模型来分析交通事故严重程度与交通环境等的关系。如K.KIM等[3]采用对数线性模型和Logistic回归模型两种方法研究了事故类型与交通事故严重程度之间的关系；C.R.MERCIER等[4]采用Logistic回归模型分析了事故严重程度与性别、年龄和乡村公路上发生的正面碰撞之间的关系；K.K.W.YAU等[5]利用Logistic回归模型分析了单车碰撞事故和多车碰撞事故的影响因素；马壮林等[6]利用Logistic 回归模型对公路交通事故严重程度影响因素进行了分析。

上述研究都只是基于平原和山区道路交通事故，较少涉及高原低氧环境下的交通事故。笔者基于青藏高原的交通事故数据，分析了高原低氧环境下交通事故严重程度的影响因素。以交通事故严重程度为因变量，选择海拔、氧含量、天气、事故地点的线形、事故地点环境、肇事车辆的类型、交通量、大车比例、大小车的速度差等9个因素为自变量，分析交通事故严重程度与这9个因素的关系，并采用Logistic回归分析建立预测模型。

1 数据收集与分析

1.1 数据收集

笔者主要采集并处理了青海省境内双车道公路的交通安全数据。青海省境内以高原地形为主，高海拔特征明显。根据研究需要，所采集的数据内容包括交通流、交通环境、交通事故、道路及路侧相关数据等。交通流数据通过对所研究的各个路段铺设MetroCount获取；交通环境数据主要包括海拔和氧含量，由手持检测设备获取；交通事故数据从当地交警部门获得，采用的完整交通事故信息为661条，其中每一条的交通事故信息包括事故发生的地点、肇事车辆的类型、肇事车辆司机的年龄、天气和事故形态等，基于交通事故信息及调研数据来探究交通事故严重程度与影响因素之间的关系；道路及路侧相关数据通过道路设计线形资料、现场调研及调研时拍摄的视频录像资料获取。

1.2 数据分析

通过对所采集的交通事故数据进行分析，笔者研究了交通事故严重程度及伤亡人数的影响因素。表1是海拔高度、大车比例、交通量、大小车速度差与平均每起事故伤亡人数的关系。由表1可见：

1)不同的海拔高度下平均每起交通事故的受伤人数和死亡人数是不同的，整体趋势上，伤亡人数随着海拔的上升而增加。说明随着海拔的增加，交通事故的严重程度也加剧。因为随着海拔的升高，含氧量降低，一方面会对驾驶员的身体状况产生影响，降低人的反应能力，造成事故的发生；另一方面会降低汽车的动力性能。

2)在道路交通中随着大车交通量所占比例的上升，交通事故严重程度明显地增大，伤亡人数明显上升。大车比例这一因素是影响重大交通事故发生的重要因素。

3)不同的交通量平均每起交通事故的受伤人数和死亡人数是不同的。整体趋势上，平均每起事故的受伤人数是随着交通量的增加而降低；平均死亡人数在交通量为4 000～6 000(含6 000)pcu/d时达到最高，在交通量>6 000 pcu/d时，则随着交通量的增加而降低。说明随着交通量的增加，公路上车辆速度相应减慢，发生交通事故的概率也会减少。

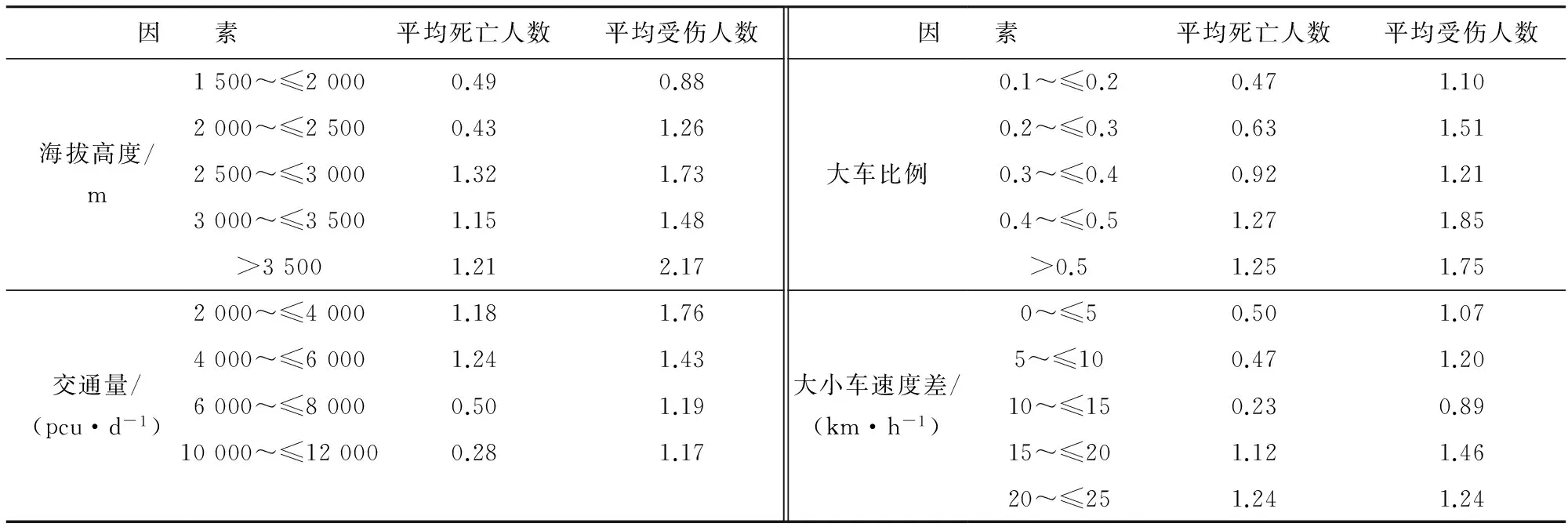
表1 海拔高度、大车比例、交通量、大小车速度差与平均每起事故伤亡人数关系

4)随着大小车速度差的增加，平均每起交通事故的受伤人数和死亡人数整体上是增加的，在速度差为15～20 km/h范围时，平均死亡人数的增长趋势较快；而平均受伤人数是有起伏的增加。

2 累积Logistic模型原理

根据因变量不同，Logistic回归模型可分为2种类型：①因变量为二分类的Logistic回归；②因变量为多分类的Logistic回归，当因变量为有序变量时，为有序多分类Logistic回归，也称之为累积Logistic回归，例如疾病的严重程度是高、中、低等；当因变量为无序多分类时，为无序多分类Logistic回归，比如倾向于选择哪种产品。笔者研究的内容为事故的严重程度，所以选用累积Logistic回归模型。

累积Logistic回归模型其实就是二分类Logistic回归模型的拓展，模型定义[7]如下：

设有序变量Y有j个等级，按顺序取值，Y取1，2，…，j，则累积Logistic回归模型可表示为

(1)

则累积Logistic回归模型可以表示为

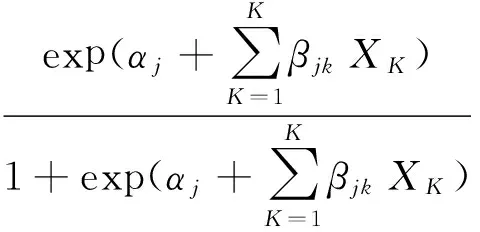
j= 1，2，…，j-1

(2)

3 变量选取及分析

3.1 因变量选取

交通事故严重程度因变量是根据每起事故的伤亡情况进行划分的。公安部于1991年发布了《关于修订道路交通事故等级划分标准的通知》，将交通事故分为轻微事故、受伤事故、重大事故和特大事故等4个等级；2004年，又发布了《交通事故统计暂行规定》，将交通事故严重程度划分为死亡事故、重伤事故、轻伤事故和财产损失事故等4个等级。

笔者参照1991年公安部的标准，结合实际调查的交通事故数据，将事故严重程度分为严重事故、受伤事故、仅财损事故3类，见表2。

表2 交通事故严重程度划分

3.2 自变量选取

根据在青海调研收集到的道路线形信息、交通流信息和交通事故信息，考虑高原特性，选出9个自变量，即海拔、氧含量、交通量、大车比例、大小车的速度差、天气、事故地点的线形、事故地点的环境、肇事车辆的类型。

3.3 变量分析

以交通事故严重程度作为因变量，其赋值及自变量的划分标准见表3。

在选定的9个因素中同时存在着定性变量和定量变量，这两类变量的赋值不尽相同。

定量变量的赋值或输入采用实际的变量值即可。研究的定量变量包括海拔、氧含量、交通量、大车比例、大小车的速度差。其中大车比例是大车数量占交通量的比例。

对于定性变量，需要引入虚拟变量。研究的定性变量包括天气、事故地点的线形、肇事车辆的类型和事故地点的环境。

1)天气。根据收集到天气信息，将天气分为晴天和非晴天，晴天赋值为0，非晴天为1。

2)事故地点的线形。根据道路全线的线形，事故发生地点线形分为在直线或平曲线上，事故地点发生在直线上赋值为0，在平曲线上为1。

3)肇事车辆的类型。交通事故信息中肇事车车辆的类型较多，笔者只分小型车和大型车2类，小型车赋值为0，大型车赋值为1。

4)事故地点的环境。笔者的研究，除穿越村镇的路段外，大量存在于山区、戈壁等无人区地带，所以根据高原地区的特殊地理环境，研究的事故地点环境分为无人区和非无人区，非无人区赋值为0，无人区赋值为1。

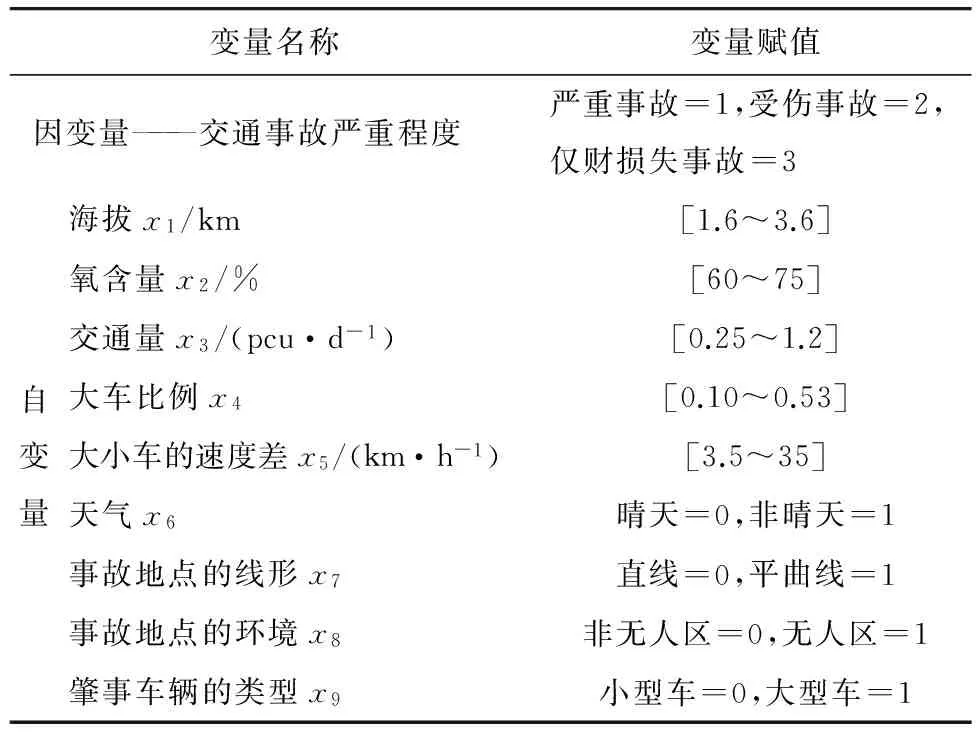
表3 变量描述

4 建立模型

根据青藏高原交通事故数据，9个因素对交通事故严重程度影响的显著性是不同的。笔者采用逐步混合选法，选择显著性高的因素进入模型。取显著性水平0.05，得到海拔、大车比例、交通量、肇事车辆和大小车的速度差这5个自变量与交通事故严重程度显著相关，见表4。

表4 参数估计值

由表4可以得到严重事故对受伤事故和仅财损事故的对数发生比，以及严重事故和受伤事故对仅财损事故的对数发生比。

由于因变量水平为3，可建立两个回归方程，故有两个常数项。而因变量为有序多分类Logistic回归的前提假设之一是，各自变量对因变量的影响是在两个回归方程中相同，所以各自变量的偏回归系数只有一个。因此，得到以下模型：

-7.10-1.41x1-2.20×10-4x3-18.23x4+0.11x5+0.89x9

(3)

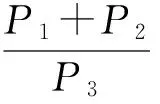
(4)

式中：P1、P2、P3为发生严重事故、受伤事故、仅财损事故的预测概率。

可以得到死亡事故和伤亡事故的累积Logistic概率预测模型：

P(Y≤1)=

(5)

P(Y≤2)=

(6)

5 模型检验

5.1 平行性检验

有序Logistic回归分析的前提是必须满足平行性检验，平行性检验即检验各自变量对于因变量的影响在各个回归方程中是否相同。进行似然比检验，若被拒绝，说明有序Logistic模型是不合适的。

表5是对模型进行平行性检验的结果，可知显著性>0.05，说明各回归方程互相平行，所有Logistic 函数都成立，累积Logistic回归模型是合适的。

表5 平行性检验

注：零假设规定位置参数(斜率系数)在各响应类别中都是相同的。

5.2 拟合度检验

表6为对模型中所有自变量偏回归系数是否全为0进行似然比检验，结果显著性<0.001,说明至少有一个自变量的偏回归系数≠0，即包含的海拔高度、大车比例、交通量、大小车的速度差、肇事车辆的类型等5个自变量的模型，其拟合效果好于仅包含常数项的无效模型。

表6 拟合度检验

5.3 准确度检验

对因变量结果预测的准确度也可以反应模型的效果。根据软件输出结果的预测类别项，输出结果计算得到的准确率为77.41%，说明模型的准确度较高。

6 结 论

基于青藏高原双车道公路实地调研数据，结合交通事故数据和交通流数据进行了分析，得到以下结论：

1)以海拔、氧含量、天气、事故地点的线形、事故地点环境、肇事车辆的类型、交通量、大车比例、大小车的速度差等为自变量，交通事故严重程度为因变量，分析了自变量与因变量之间显著相关关系。研究发现：海拔、大车比例、交通量、肇事车辆的类型和大小车的速度差这5个自变量与交通事故严重程度显著相关。

2)以交通事故严重程度为因变量，海拔、大车比例、交通量、肇事车辆和大小车的速度差这5个为自变量，采用累积Logistic回归模型建立交通事故严重程度的预测模型。通过对模型验证，其准确性和拟合度的检验效果都比较高。

[1] 公安部交通管理局.中华人民共和国道路交通事故统计年报(2013年度)[R].无锡:公安部交通管理科学研究所,2014:139. Traffic Management Bureau of Ministry of Public Security.ChineseAnnualReportonRoadTrafficAccidentStatistics: 2013 [R]. Wuxi: Traffic Management Research Institute of the Ministry of Public Security, 2014: 139.

[2] 王谦,俞祥海,胡湘林,等.1894例青藏高原道路交通伤分析[J].中华创伤杂志,2004,20(3):136-138. WANG Qian, YU Xianghai, HU Xianglin, et al. Analysis on 1894 cases of road traffic injuries in the Qinghai-Tibet plateau [J].ChineseJournalofTrauma, 2004, 20(3):136-138.

[3] KIM K, NITZ L, RICHARDSON J, et al. Analyzing the relationship between crash types and injuries in motor vehicle collisions in Hawaii [J/OL].TransportationResearchRecord,1994,1467:9-13[2016-07-21]. http://onlinepubs.trb.org/Onlinepubs/trr/1994/1467/1467-002.pdf.

[4] MERCIER C R, SHELLEY L M C, ADKINS G H, et al. Age and gender as predictors of injury severity in head-on highway vehicular collisions[J/OL].TransportationResearchRecordJournaloftheTransportationResearchBoard, 1997, 1581 (1): 37-46 [2016-07- 21].http://trrjournalonline.trb.org/doi/pdf/10.3141/1693-09.

[5] YAU K K W, LO H P, FUNG S H. Multiple-vehicle traffic accidents in Hong Kong [J/OL].AccidentAnalysis&Prevention, 2006, 38 (6): 1157 -1161[2016-07-21].http://ac.els-cdn.com/S0001457506000807/1-s2.0-S0001457506000807-main.pdf?_tid=1a163c4a-57c2-11e7-bceb-00000aacb361&acdnat=1498187863_4e467bc07603b17e4bd21ffad7473a56.

[6] 马壮林,邵春福,李霞.基于Logistic模型的公路隧道交通事故严重程度的影响因素[J].吉林大学学报(工学版), 2010, 40(2): 423- 426. MA Zhuanglin, SHAO Chunfu, LI Xia. Analysis of factors affecting accident severity in highway tunnels based on Logistic model [J].JournalofJilinUniversity:EngineeringandTechnologyEdition, 2010, 40 (2): 423-426.

[7] 王济川,郭志刚.Logistic 回归模型——方法与应用[M].北京:高等教育出版社,2001:237-239. WANG Jichuan, GUO Zhigang.LogisticRegressionModel:MethodsandApplications[M].Beijing:Higher Education Press,2001: 237-239.

(责任编辑：田文玉)

Establishment of Accident Severity Prediction Model of Two-Lane Highway on Qinghai-Tibet Plateau

SUN Xiaoduan, HOU Yangyang, HE Yulong, FENG Bingbing

(Beijing Key Laboratory of Traffic Engineering, Beijing University of Technology, Beijing 100124, P. R. China)

Based on the analysis of traffic accident data of Qinghai-Tibetan plateau, it is found that most of the traffic accidents are of high casualties, which means the proportion of accidents with deaths and injuries is relatively larger. The cumulative Logistic regression was used to research the factors which affected the severity of traffic accidents in plateau area. The collected accident severity was selected as the dependent variable. The altitude of the environment, the oxygen content, the weather, the linear and environment of the accident site, the type of the vehicle, the traffic volume, carts ratio, the speed difference between cart and car were selected as independent variables. Therefore, the cumulative Logistic regression model was established. The results show that five independent variables including altitude, carts ratio, the vehicle type and the speed difference between the cart and the car are significantly correlated with the severity of accident. This prediction model can provide theoretical basis for the related highway management departments to make safety measures.

traffic engineering; cumulative Logistic model; Qinghai-Tibet plateau; accident severity prediction

10.3969/j.issn.1674-0696.2017.07.18

2016-08-27；

2017-03-30

国家科技支撑计划课题(2014BAG05B02)

孙小端(1956—)，女，美籍华人，教授，博士生导师，主要从事交通安全方面的研究。E-mail：bjut2003@gmail.com。

U491.31

A

1674-0696(2017)07-106-05