基于模糊信息粒与SVM的道路交通状态波动分析

陆百川,李晓璐,郭桂林,黄梨力

(1. 重庆交通大学 交通运输学院，重庆 400074；2. 重庆交通大学 重庆山地城市交通系统与安全实验室，重庆 400074)



基于模糊信息粒与SVM的道路交通状态波动分析

陆百川1,2,李晓璐1,郭桂林1,黄梨力1

(1. 重庆交通大学 交通运输学院，重庆 400074；2. 重庆交通大学 重庆山地城市交通系统与安全实验室，重庆 400074)

为分析道路交通状态波动范围，提出了一种基于模糊信息粒化与支持向量机组合预测的建模方法。分析了道路交通状态波动特点和交通参数选择原则，以模糊理论和时间序列预测为基础，通过模糊信息粒以15 min时间窗将样本数据模糊化，得到Low、R、Up这3组时间序列；并利用支持向量机模型分别对其进行预测，获得道路交通状态的波动范围与变化趋势。实例分析时，在验证数据采集路段属性相近的前提下，用该组合模型对早、晚高峰和平峰等3个时段的交通波动状态进行验证，验证结果有较高精度，能有效预测交通状态波动情况。

交通工程；交通状态；波动范围；模糊信息粒化；支持向量机

0 引 言

对交通状态的波动进行准确估计与分析能够为相关部门有针对性地制定交通管控措施提供可靠依据，提高路网的利用率，保障道路交通更加通畅；同时也将为出行者提供路段交通状态变化趋势，从而合理规划出行路线。随着信息技术的发展，通过对海量的道路交通数据挖掘，分析道路交通状态波动范围成为当前的研究热点之一。

刘晓玲等[1]在对多维时空参数进行分析的基础上，提出利用支持向量机(SVM)对不同维数的路段交通状态进行短时预测；董宏辉等[2]通过提取对道路交通状态有显著影响的时空特征，利用最大熵模型训练获得不同影响特征的权重，从而对路段交通状态等级进行直接预测；刘擎超等[3]通过构建神经网络分类器的能力区域，通过计算样本数据与交通状态类簇之间的空间距离，对道路交通状态进行预测；钱民等[4]提出了一种从系统的角度出发，通过定性动态概率网络方法对交通状态进行预测及改进；康海贵等[5]提出基于混沌Logistic映射和云自适应机制对标准的遗传算法进行改进，建立了基于混沌云自适应遗传算法进行SVR参数优选CCLGA-SVR城市主干道短时交通流量预测模型。上述研究多以提高状态预测的准确性为主，若可对交通状态变化范围进行有效预测，则能提前评估其对路网造成的影响，从而使交通管理部门采取有效措施分担路网交通压力。

目前对道路交通状态的研究只是停留在点时间的预测，而忽视了交通状态的波动情况，笔者提出了基于模糊信息粒化和SVM的预测模型对交通状态波动进行分析。首先，以15min为操作窗口，利用三角型模糊信息粒将样本数据模糊化，得到Low、R、Up等3组时间序列；然后分别以Low、R、Up作为输入，通过支持向量机模型分别对其进行预测，从而获得路段交通状况的波动范围及其变化趋势；最后，经重庆市龙腾大道部分路段实测数据仿真分析，证明了笔者提出模型的有效性。

1 交通状态波动特征与参数选择

1.1 交通状态波动特征

交通状态波动是指在一定时间内交通状态变化的范围，交通状态波动分析可从不同层次、不同维度定量地分析交通流运行的状况，能够有效的识别交通流运行中的薄弱环节，掌握交通流演变的规律，为交通管理部门制定合理的交通管控措施提供可靠依据。

交通状态波动反映的是某路段整个交通流运行的情况，通常交通状态波动变化具有以下几个特征：

1)时间属性。交通状态波动是交通流在一段时间内运行变化的客观反映，在相同路段，不同时间交通状态波动也不尽相同，具有时间属性。

2)空间属性。交通状态波动随空间变化而变化，在相同时间，不同路段交通状态波动也不尽相同，具有空间属性。

3)对象属性。交通状态波动是从宏观层面分析交通情况，是以路段中所有交通流为一个整体而言。

4)条件属性。交通状态波动反映的是交通流的运行情况，只有交通流行为改变才能产生新的交通状态波动。

5)结果属性。交通状态波动是衡量交通流运行优劣的定量指标，可以根据交通流行为预测波动范围，具有可预测性。

1.2 交通参数选择原则

选择合理且可靠的交通参数进行路段交通状态的预测，不仅减少了前期数据处理的工作量，同时能够提高后续预测模型的精度。笔者通过以下几个原则进行交通参数的选取：

1)直观性。即交通参数的变化容易被觉察和理解。如：车速，当行驶路段畅通时，车辆能够以较快的速度通行；反之，车辆行驶缓慢；

2)便捷性。即所选交通参数能够直接获取。如：密度，该参数直观性较好，然而，目前的检测技术，只能通过计算间接得到该参数。这样不仅增加数据准备的工作量，还使实时性大打折扣；

3)灵敏性。即所选的交通参数对当下的交通状态反映迅速，大体上能实时响应道路交通状态的波动变化。

考虑上述3个原则的分析，交通流速度参数能够及时、直观地反映交通状态的变化情况。故而，笔者以交通流速度为研究对象，对交通状态的波动及其变化趋势进行分析。

2 交通状态波动需求

交通状态波动分析是以交通流理论为基础，研究交通流的时空变化特征。通过对交通状态波动分析，可以发现交通流运行模式及变化规律，以便建立相应模型深入研究。

从需求者角度而言，交通状态波动分析主要服务于两类需求者，一类是交通出行者，如乘客和驾驶员；另一类是交通管理者，如交通管理部门、公交公司，道路建设部门等。两类需求者对交通状态波动分析功能需求如表1。

表1 不同对象交通信息需求分析

交通管理者通过对交通流运行情况进行分析、判断及预测，从而采取相应措施，影响出行者的交通行为。同时，出行者通过获取的交通状态波动情况，选择合适的出行路线、出行时间及出行方式，以致于又影响了交通流运行状况。因此，两者相互联系，又相互影响。由表1中两者需求目的可以看出：交通出行者更关注个体的出行成本，通过对交通状态波动情况分析，选择适当的出行路线，使得自身的出行延误最小；而交通管理者更注重整个路网的运行情况，通过分析交通状态波动情况，及时、科学地制定交通管控措施，最大限度的提高路网的利用率。

同时，对交通状态波动情况的分析，将道路交通状态识别由点扩展到了面。一般地，预测道路交通状态都是通过分析历史交通数据，建立数学模型，然后对点时间的预测。然而，出行者的出行时间通常是模糊的，是在一个时间段内。因此，精确时间点交通状态预测的应用就受到了很大的限制。而分析交通状态波动情况，则可将交通状态的判断由点时间拓展到一个时间段内，通过分析一定时间段的交通状态波动范围，从而为交通出行者和管理者的决策提供依据，提高了交通状态预测的价值。

3 模糊信息粒化和SVM原理

3.1 模糊信息粒化

L．A．ZADEH[6]提出了信息粒化的概念，其核心思想为：通过分析事物内部特征，将属性相似，功能相同的部分视为一个个体，从而将整体划分为多个个体，这些个体称为信息粒。其本质就是将事物整体划分为独立的个体进行研究。

在实际采集的交通数据中通常存在不同的数据类型，表征的属性也不同，往往很难用特定的模型对其进行表示。模糊信息粒化用模糊集的形式表达信息粒，通过模糊集的方法对时间序列进行信息粒化，主要分为两个过程：窗口划分和模糊化。所谓窗口划分，即将给定的一段完整的时间序列按实际需求的时间间隔划分为若干子序列，作为操作窗口；模糊化处理，即将操作窗口中的数据进行模糊处理，生成相应模糊集，结合上述两个过程就是模糊信息粒化[7]。

目前实际分析中常用的模糊信息粒形式有：三角型、梯形、高斯型和抛物线型等，不同模糊信息粒形式如图1。

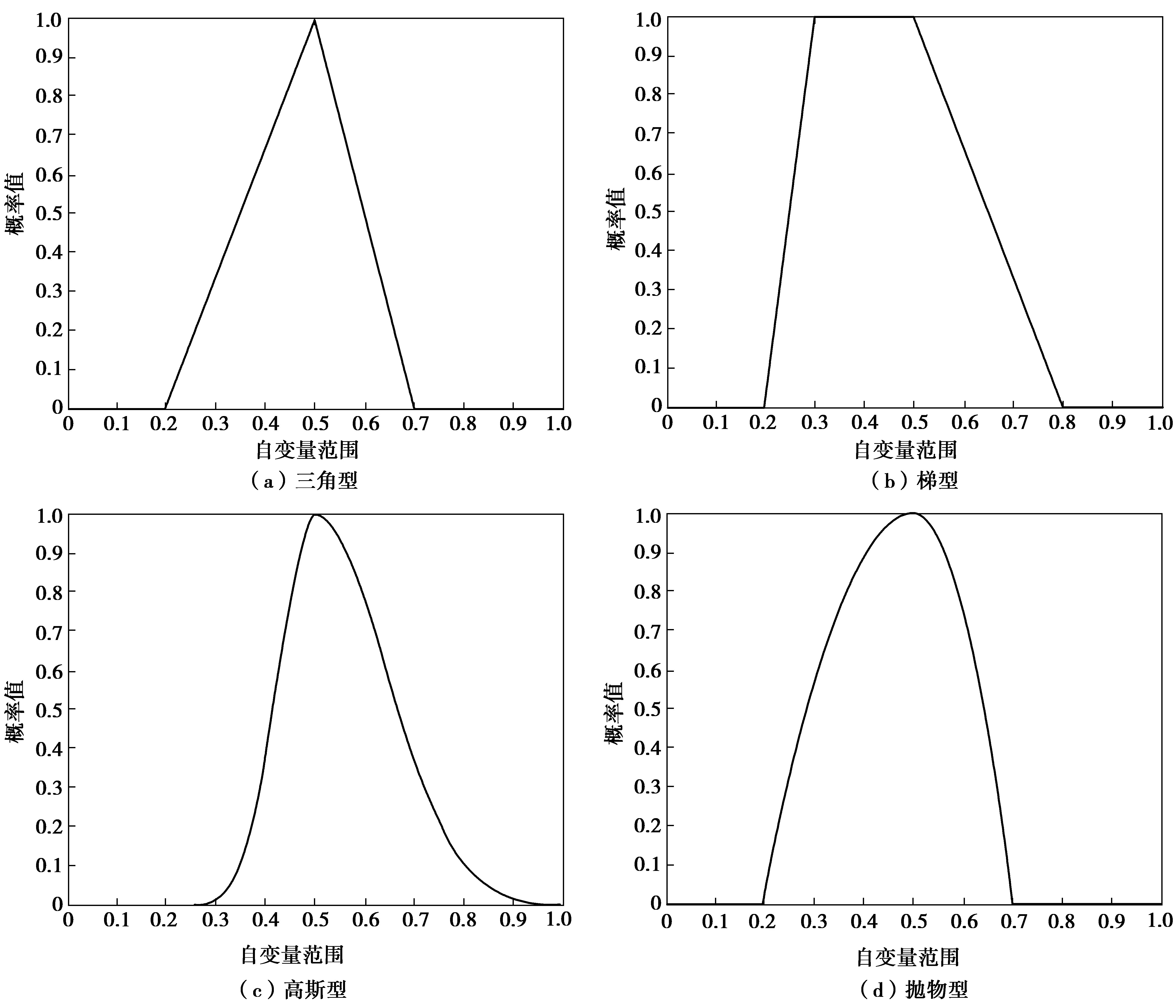
图1 不同模糊信息粒隶属度函数Fig. 1 Different membership functions of fuzzy information granules

3.2 支持向量机

交通流速度序列具有高度的非线性、复杂性和随机性，若以传统的数学方法来对其进行趋势预测，往往难以满足后续应用的要求。支持向量机(support vector machines，SVM)具有以下几个方面优势：

1)理论基础完善。以统计学为理论基础，具有较强的学习能力。

2)能够获得全局最优解。该方法将传统优化问题转化成对凸二次规划的求解问题，其中，二次规划问题的解通常是唯一的全局最优解，避免了局部最优解的困扰。

3)结构风险最小原则。该原则提高了模型的泛化能力，在各领域有广泛的应用。

4)克服了维数灾难。通过核函数学习机制，在分析非线性、高维模式识别问题时很大程度上克服了“维数灾难”和“过学习”等问题。

4 交通状态波动范围预测模型

模糊信息粒化是将一个整体中属性相似、功能相近的个体划分在同一操作窗口内，利用个体间的信息共享和相互协作找出最优解[8]；支持向量机以结构风险最小化原则，在小样本、随机性较强的时间序列预测中有突出的表现，结合两者的优势，针对交通状态波动范围分析，建立基于模糊信息粒化与支持向量机的组合预测模型。

4.1 交通流速度数据模糊化

4.1.1 窗口划分

在构建模糊信息粒子之前，需要选择一定长度的窗口，将原始时间序列划分为多个小的子序列，由于窗口长度的确定存在一定的主观性，不同的划分方式对实际的预测也会产生不同的影响。根据交通状态波动特征，以15 min时间窗将样本数据进行分割，设置操作窗口的长度为3，即每个粒化窗口中包含3个周期的数据，那么，原数据长度除以3后取整为最终粒化窗口个数。

4.1.2 数据模糊化处理

在每个子序列窗口建立模糊粒子是模型中的关键。由于笔者要对道路交通状态波动范围进行分析预测，通过窗口内的最大值和最小值信息能够获得波动区间。故而笔者选取三角型模糊信息粒对数据进行处理，其隶属度函数表示为：

(1)

式中：x为论域中的变量；a、m、b分别为各窗口进行模糊信息粒化处理后所得3个变量Rlow、Raverage和Rup参数，其中RLow表示交通状态波动的最小值，Raverage表示交通状态波动的平均值，Rup表示交通状态波动的最大值。

采用三角型模糊信息粒计算参数Rlow，得到交通状态波动最小值。

(2)

采用三角型模糊信息粒计算参数Raverage，得到交通状态波动平均值。

(3)

采用三角型模糊信息粒计算参数Rup，得到交通状态波动最大值。

(4)

4.2 支持向量机预测过程

4.2.1 样本数据预处理

为避免数值较大的数据覆盖数值较小的数据情况的发生，使得数据之间具有可比性，需要对训练数据进行预处理。首先分别对模糊信息粒化后得到的交通状态波动最小值Rlow、平均值Raverage和最大值Rup进行归一化处理[9]，如式(5)：

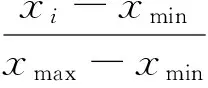
(5)

式中：xmin为原始数据最小值；xmax为原始数据最大值；xi为原始数据；pi为归一化后的数据。

4.2.2 模型参数确定

由于SVM属于“黑箱操作”模式，难以直接求得最优解，因此，采用模式搜索算法，训练SVM，并确定最优参数C和g，构建交通状态波动预测模型。

4.2.3 模型预测

利用最优参数C和g建立SVM预测模型，以预测数据为输入，预测下一个时间窗口内交通状态波动的最小值Rlow、平均值Raverage和最大值Rup。

4.2.4 检验模型预测效果

对SVM的预测结果进行分析，分析预测值与真实值的误差情况，评估预测模型的优劣。

4.3 分析交通状态波动范围

由SVM回归模型分别对模糊粒子参数Rlow，Raverage和Rup进行预测，从而得到交通状态波动的最小值、平均值和最大值，分析3者之间的关系，进而确定交通状态波动范围。

基于模糊信息粒化的SVM组合预测模型预测过程如图2。模糊信息粒化以粒子为单位处理信息，通过对交通流速度数据进行有效挖掘，并以挖掘得到的有效数据建立交通状态波动预测模型。

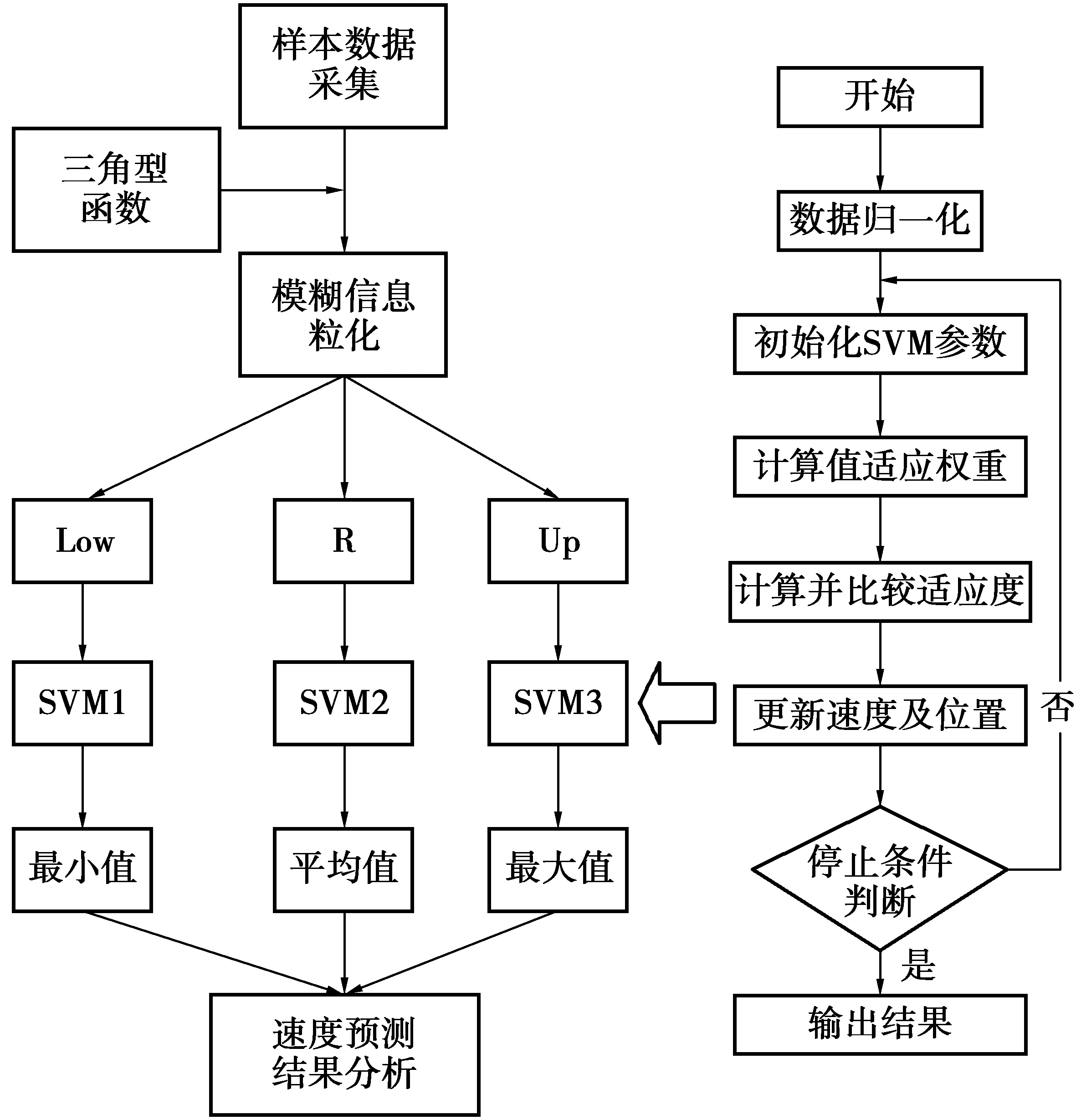
图2 基于模糊信息粒化的SVM组合模型流程Fig.2 Flow chart of the combined model based on fuzzy information granulation and SVM

5 案例分析

5.1 路段属性相似性分析

笔者选取了重庆市龙腾大道，它是重庆市主干道之一，约为4 km，途经陈家坪立交、大公馆立交、谢家湾立交和多个交叉口，双向6车道。首先以交叉口为节点简单将干道分为5段： 陈家坪立交—科园四路—科园六路—大公馆立交—谢家湾立交—鹅公岩大桥。然而，简单的以交叉口为节点的分段方式并不合理，这里文章选取了道路固有属性，如路段长度、路面情况、坡度、车道数和路段动态影响因素，如路段平均行驶速度，道路的交通管控措施等，进一步将各路段以属性相似性为依据进行重新聚类。具体步骤为：①对选取的各影响因素进行归一化处理，如表2；②构建5个行向量，向量分别为各路段影响因素归一化后的数据；③计算各向量间距离同时进行聚类，并绘制聚类谱系图。

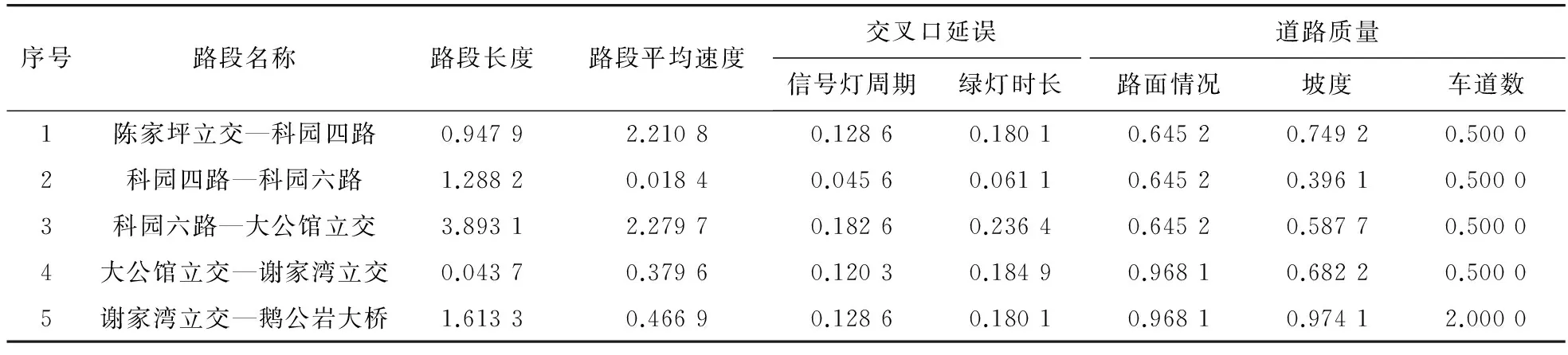
表2 各影响因素数据归一化结果

在SPSS统计软件中，将5组行向量以组间联接的方式进行系统聚类，用平方Euclidean距离作为度量标准，根据路段各不同影响因素进行聚类分析，得到聚类谱系数图，如图3。由路段间各属性相似性为依据，将龙腾大道各路段分为3类：路段2、4、5；路段1；路段3。

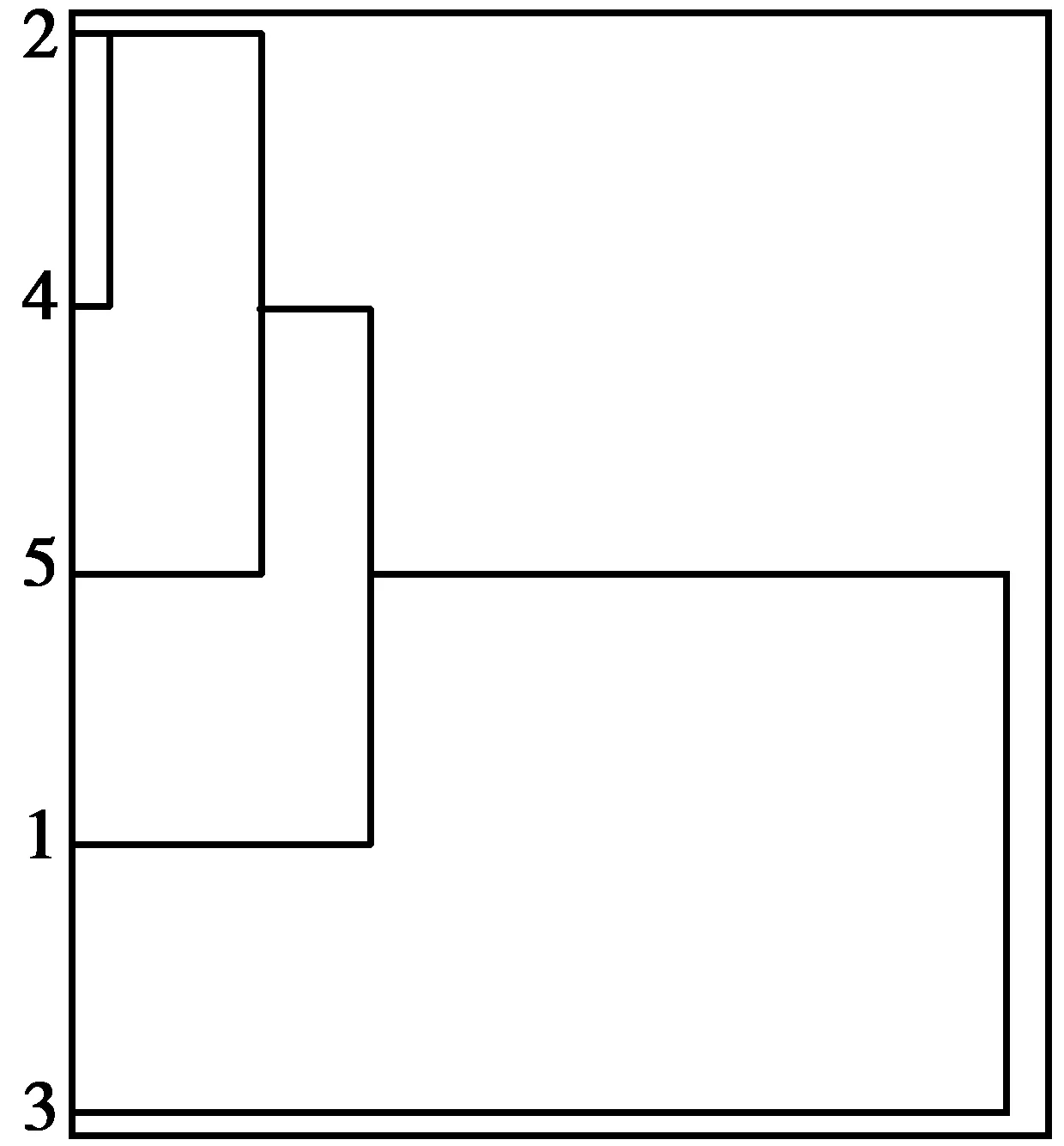
图3 路段聚类谱系图Fig. 3 Cluster spectrum diagram of road segment

显然，考虑多因素后将龙腾大道以相似性分为3类的路段分类方式比单一的以交叉口为节点分段方式减少了计算量，同时，由于聚类时考虑了路段上的动静态因素，因此在理论上更具有可信度。所以笔者选取聚类后的分段结果来对所提出的模型进行验证。

5.2 数据准备与结果分析

笔者进一步选择3段中的一段，科园六路—大公馆立交，2014年12月15日—19日的出租车GPS数据为基础。由于所采集数据的时间属性有较大变化，分为3个时段“早高峰时段—平峰时段—晚高峰时段”进行分析，数据以5 min为周期，以前4 d的3个时段的数据作为训练样本，19日的数据作为预测样本。模糊信息粒化以3为数据窗口长度，即以3个周期为一个操作窗口。前4 d每个时段的数据均被分成了96个时间窗口，分别对每个时段时间窗口的数据进行验证。限于篇幅，在每个时间段内，笔者分别随机抽取两个时间窗口记为win_num1，win_num2。通过三角型模糊粒子对交通流速度序列进行信息粒化处理，得到3组时间序列Rlow、Raverage和Rup，如图4。

图4 交通流速度曲线与速度值模糊信息粒化Fig. 4 Traffic flow velocity curve and fuzzy information granulation of traffic flow velocity

图4中：当车辆在路段上匀速行驶时，将其进行模糊信息粒化处理后，获得的Rlow、Raverage和Rup这3个参数的值高度吻合，表明该时段内交通运行稳定，交通流速度没有明显波动。而当道路上交通流速度明显变化时，其模糊信息粒化后所得的Rlow、Raverage和Rup这3参数值也有明显波动。

依次分别将3个时段速度值进行模糊信息粒化处理后得到的Rlow、Raverage和Rup三序列分别作为SVM的输入，同时，对SVM模型进行参数寻优，最后利用此模型对路段交通状态短时变化趋势进行预测。限于篇幅，笔者选择早晚高峰对所提模型进行验证，同时为了说明文中提出模型的有效性，在使用同样的样本数据条件下，在模糊信息粒化后使用Elman神经网络进行相应的回归预测，其预测结果见表3。

根据表3可知，基于模糊信息粒的SVM模型能够准确地描述速度波动范围。就晚高峰时段，将时间窗口win_num1和win_num2中实际数据由小到大排列，分别为[50.290 1 54.496 4 56.995 3]、[45.062 3 49.112 3 49.803 0]。参数Rlow、Raverage和Rup准确地对实际交通流速度波动范围进行了描述，窗口win_num1的预测结果中下限溢出即路段交通状态有恶化趋势，而窗口win_num2的预测结果中上限溢出，说明路段交通状态未达到最佳状态，仍有较大的改善空间。在时间窗口win_num1内，交通状态波动范围为9.33 km/h；而在时间窗口win_num2内，交通状态波动范围为10.49 km/h。在这两个时间窗口内，道路交通运行稳定，波动较小。同理可以分析早高峰时段和平峰时段的交通状态波动情况。

通过对比SVM和Elman预测结果可知，在早高峰两个时间窗口内SVM对Rlow、Raverage和Rup预测其平均误差分别为0.497%、2.541%、0.875%；而Elman预测结果平均误差分别为1.621%、3.184%、2.064%。

在晚高峰两个时间窗口内SVM对Rlow、Raverage和Rup预测其平均误差分别为1.715%、2.189%、3.744%，而Elman预测结果平均误差分别为4.029%、5.096%、2.319%。由此可见，笔者提出的模型具有更高的精度。

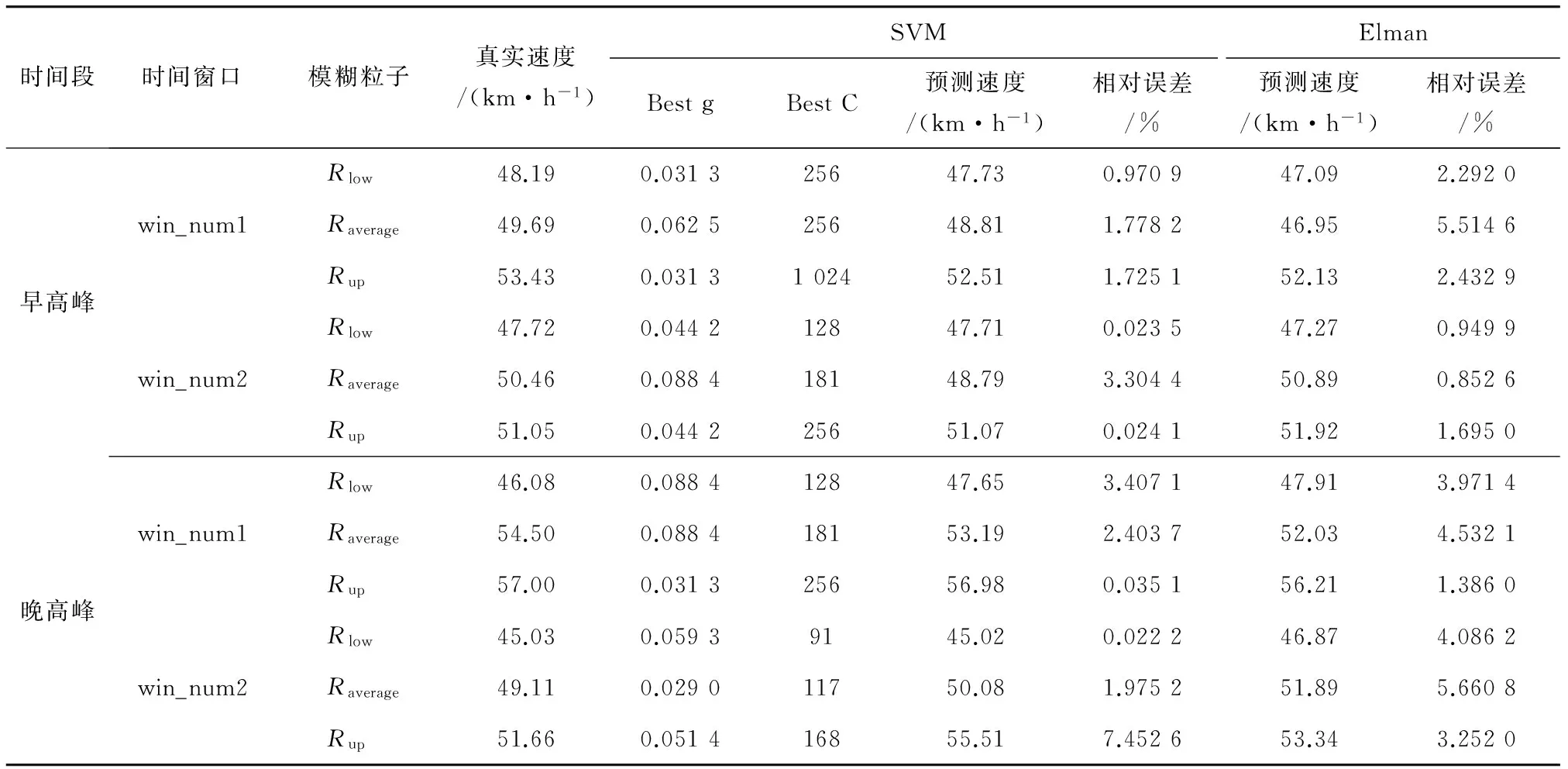
表3 SVM和Elman预测结果对比

6 结 论

笔者对道路交通状态波动情况进行了研究，分3个时段“早高峰时段—平峰时段—晚高峰时段”进行分析。

首先，以模糊集理论为基础，以3个周期数据为操作窗口，利用三角型模糊信息粒将样本数据模型化，得到分别表示交通状态变化的最小值Rlow、平均值Raverage和最大值Rup；之后将Rlow、Raverage和Rup作为SVM模型和Elman神经网络的输入，并对SVM进行参数寻优，得到交通状态波动情况；最后经实例分析，比较SVM模型和Elman神经网络预测结果可知：笔者所提出的模型具有更高的预测精度，能够有效预测交通状态波动范围。

[1] 刘晓玲，贾鹏，邬珊华，等．基于多维时空参数的道路短期交通状态预测[J]．交通运输系统工程与信息，2011，11(4)：140-146． LIU Xiaoling, JIA Peng, WU Shanhua, et al. Short-term traffic flow forecasting based on multi-dimensional parameters [J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2011, 11(4): 140-146.

[2] 董宏辉，贾利民，孙晓亮，等．基于最大熵模型的城市快速路交通状态预测方法研究[J]．交通运输系统工程与信息，2010，10(2)：112-116． DONG Honghui, JIA Limin, SUN Xiaoliang, et al. Traffic state forecasting towards urban freeway based on the maximum entropy model [J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2010, 10(2): 112-116.

[3] 刘擎超，陆建，陈淑燕．基于能力区域的交通状态预测方法[J]．物理学报，2014，63(14)：94-101． LIU Qingchao, LU Jian, CHEN Shuyan. Traffic state prediction based on competence region [J].ActaPhysicaSinica, 2014, 63(14): 94-101.

[4] 钱民，唐克生．基于定性动态概率网络的交通状态预测及改进[J]．云南大学学报(自然科学版)，2012，34(2)：165-168． QIAN Min, TANG Kesheng. Traffic state prediction and improvement based on qualitative dynamic probabilistic networks [J].JournalofYunnanUniversity(NaturalSciencesEdition), 2012, 34(2): 165-168.

[5] 康海贵，莫仁杰，李明伟，等．基于云遗传算法优选的SVR交通量预测模型[J]．武汉理工大学学报(交通科学与工程版)，2013，37(2)：225-229． KANG Haigui, MO Renjie, LI Mingwei. Urban traffic flow forecasting base on CCLGA algorithm optimizes parameters of SVR [J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering), 2013, 37(2): 225-229.

[6] ZADEH L A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic [J].FuzzySetsandSystem, 1997, 90(2): 111-127.

[7] PEDRYCY W.GranularComputing:AnIntroduction[M].Dodrecht: Kluwer Academic Publishers, 2003.

[8] 彭勇，陈俞强．基于信息粒化的SVM时序回归预测[J]．计算机系统应用，2013，22(5)：163-167． PENG Yong, CHEN Yuqiang. Time series regression and prediction based on information granulation and SVM [J].ComputerSystems&Applications, 2013, 22(5): 163-167.

[9] 黄艳国，许伦辉，邝先验．基于模糊C均值聚类的城市道路交通状态判别[J]．重庆交通大学学报(自然科学版)，2015，34(2)：102-107． HUANG Yanguo, XU Lunhui, KUANG Xianyan. Urban road traffic state identification based on fuzzy C-mean clustering [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34(2): 102-107.

[10] 史峰，王辉，胡斐，等．MATLAB智能算法30个案例分析[M]．北京：北京航空航天大学出版社，2011． SHI Feng, WANG Hui, HU Fei, et al. 30IntelligentAlgorithmCaseAnalysisBasedonMATLAB[M]. Beijing: Beihang University Press, 2011.

[11] 田保慧，郭彬．基于时空特征分析的短时交通流预测模型[J]．重庆交通大学学报(自然科学版)，2016，35(3)：105-109． TIAN Baohui, GUO Bin. A short-term traffic flow prediction model based on spatio-temporal characteristics analysis [J].JournalofChongqingJiaotongUniversity(NatureScience), 2016, 35(3): 105-109.

(责任编辑：刘 韬)

Fluctuation Analysis on Road Traffic State Based on Fuzzy InformationGranulation and Support Vector Machine

LU Baichuan1, 2, LI Xiaolu1, GUO Guilin1, HUANG Lili1

(1. School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, P. R. China;2. Key Lab of Traffic System & Safety in Mountain Cities, Chongqing Jiaotong University, Chongqing 400074, P. R. China)

In order to analyze the range of traffic state fluctuation, a combined modeling method of forecasting the range of traffic state fluctuation based on fuzzy information granulation and support vector machine was put forward. The fluctuation characteristics of road traffic state and the selection principles of traffic parameters were analyzed on the basis of fuzzy theory and time series prediction. The sample data were fuzzed by 15 min time window through the fuzzy information granules, and three sets of time series, including Low, R and Up, were obtained. The support vector machine was used to forecast each set of time series, and the traffic state fluctuation range and variation tendency were obtained. In case studies, in the premise of verification data acquisition segment with similar attributes, the proposed model was used to analyze the fluctuation of traffic state in morning, evening peak periods and peace period, whose results were of high accuracy and could effectively predict the fluctuation of traffic state.

traffic engineering; traffic state; fluctuation range; fuzzy information granulation; support vector machine

10.3969/j.issn.1674-0696.2017.07.14

2016-05-02；

2016-09-07

陆百川(1961—)，男，江苏南通人，教授，博士生导师，主要从事交通信息工程及控制方面的研究。E-mail：baichuan@cqjtu.edu.cn。

李晓璐(1992—)，女，新疆乌鲁木齐人，硕士研究生，主要从事交通信息工程及控制方面的研究。E-mail：rolista1120@163.com。

U491.1+23

A

1674-0696(2017)07-083-07