忆感器文氏电桥振荡器∗
许碧荣 王光义
1)(杭州电子科技大学,现代电路与智能信息研究所,杭州 310018)
2)(武夷学院机电工程学院,武夷山 354300)
忆感器文氏电桥振荡器∗
许碧荣1)2)王光义1)†
1)(杭州电子科技大学,现代电路与智能信息研究所,杭州 310018)
2)(武夷学院机电工程学院,武夷山 354300)
(2016年7月29日收到;2016年11月5日收到修改稿)
为了探索新型忆感器的特性,提出了一种新的忆感器模型,该模型考虑了内部变量的影响,更符合未来实际忆感器的性能.建立了其等效电路,分析了其特性.利用该忆感器模型,设计了一种忆感器文氏电桥混沌振荡器,分析了系统的稳定性和动力学行为.研究发现,此系统不仅存在周期、拟周期和混沌等多种状态,还发现了一些重要的动力学现象,如恒Lyapunov指数谱、非线性调幅、共存分岔模式和吸引子共存等复杂非线性现象,说明了这些特殊现象的基本机理和潜在应用.最后进行电路实验验证,验证了该振荡器的混沌特性.
忆感器,文氏电桥,混沌,吸引子共存
1 引 言
Chua(蔡少棠)在1971年提出忆阻器模型[1],2008年,HP实验室实现了纳米级忆阻器[2,3].由于忆阻器在存储、神经网络和电路设计等多方面具有潜在的应用价值,因此引起了学术界的广泛兴趣[4-9].2008年,Di Ventra等[10]将忆阻器概念进行拓展,提出了忆感器和忆容器.但是,相对于忆阻器而言,对忆感器和忆容器的研究相对较少,有必要开展忆感器和忆容器物理特性及其应用的预先研究.
忆容器和忆感器的概念最早出现在1978年的欧洲电路理论与设计会议(ECCTD)上,由Chua[11]在其特邀报告中作为两种新型电路元件而提出,2003年Chua[12]正式定义了此两种记忆元件,尤其给出了电路元件的(α,β)阶分类,把忆阻器、忆感器和忆容器分别定义为(-1,-1)阶、(-2,-1)阶和 (-1,-2)阶电路元件.2008年,Di Ventra等[10]在伯克利举行的忆阻器研讨会上正式提出了忆感器和忆容器的定义与电路符号.2009年Chua[13]在IEEE专家短训班上的辅导报告可帮助读者进一步理解忆感器的概念.
虽然还未报道物理实现的忆感器元件,但已经发现或预测了忆感现象的存在.可以设想,一个简单的实际忆感器可用某种磁芯材料来实现,其忆感效应依赖于磁场的历史[10].实际上已经发现某些绝缘材料具有忆感器效应[14],也出现了利用自旋霍尔磁电阻实现忆感器的报道[15].
忆感器建模是忆感器特性和应用研究的基础.因此,自忆感器提出之后,出现了一些接地和浮地的忆感器模拟器[16-20]和SPICE模型[21,22],用以仿真忆感器的物理特性.文献[15]提出了忆感器的一种物理实现的方法,文献[19,23]分析了忆感器串并联的规律.由于忆感器与忆阻器一样也具有非线性记忆特性,也可利用它来设计混沌振荡器,近来出现了少量对忆感器混沌振荡器的研究[24,25].然而文献[24,25]采用了较理想的忆感器模型,未考虑忆感器内部变量的影响,其忆感器振荡器基于Chua电路来设计,含有线性电感元件,体积大难以集成化,难以产生低频信号,且其实验电路为基于数学模型的等效运算电路,而非基于实际元件建立的实际电路.而文氏电桥混沌振荡器[26,27]具有振荡稳定、波形良好和振荡频率宽等优点.然而,到目前为止未出现任何形式的忆感器文氏电桥混沌振荡器,因此,有必要开展这方面的研究,探索忆感器文氏电桥振荡器的特性.
本文将忆感器模型进行拓展,提出了一种新的模型,该模型考虑了忆感器内部变量的影响,建立其等效电路,分析其特性,并在此基础上,设计了一种基于忆感器的文氏电桥混沌振荡器,分析了其动力学特性,并进行电路实验验证.与文献[24]等相比,该振荡器还出现了一些重要的特殊现象,如恒定Lyapuno指数与恒定混沌振荡、非线性调幅、共存吸引子和共存分岔等.
2 忆感器模型及其等效电路
文献[10]提出了忆感器的一般概念与一般模型,时不变忆感器可定义为

式中L-1是电感的倒数,iM是流过忆感器的电流,φ是忆感器的磁通量,ρ是忆感器的内部状态量.
从(1)式看出,一般情况下状态变量的变化率dρ/dt与磁通和该变量自身相关.但为了简便,对忆阻器、忆容器和忆感器的建模大都采用一种特例下的简化模型,即忽略内部变量ρ对dρ/dt的影响.如在HP忆阻器中仅考虑电荷的影响[3], 即 dρ/dt=f(ρ,q)=aq, 其中a为系数;在忆感器模型中仅考虑磁通φ的影响[10],即dρ/dt=f(ρ,φ)=Aφ,其中A为系数,这些模型可认为是理想模型.
而实际器件的内部情况要复杂得多,往往要考虑内部状态变量ρ对其导数的影响(这个导数可能是粒子的漂移速率,如HP忆阻器;或是磁性材料中引起电感变化的磁性材料某种参数的变化率).例如,文献[3]在提出忆阻器简化的理想模型之后,为考虑实际器件内部变量的影响,在内部变量w的导数dw/dt中增加了一个关于变量w函数的乘积项;从已实现的忆阻器看,许多忆阻器并不是理想的忆阻器模型,而是广义的忆阻器模型或忆阻系统[2,3,28,29].忆感器较忆阻器难以实现,但从文献[15]利用自旋霍尔磁电阻实现的一种忆感器看,其模型并不是理想模型.因此,从一般意义考虑并着眼于未来可实现的实际忆感器,其内部状态量ρ对时间t的导数,一般情况下会受内部状态量自身的影响.考虑了这个因素后,本文提出如下忆感器模型:

其中A,B,C,D为系数,ρ为忆感器内部状态变量(对应(1)式的x)f(ρ,φ)=Aφ-Bρ中的第一项Aφ为磁通对dρ/dt的贡献,第二项Bρ反映了忆感器内部状态变量对其变化率的影响.(2)式与(1)式相比,忆感倒数为L-1(ρ,φ)=Cρ/φ-Dρφ.该忆感倒数反映了在一个实际的忆感器中,其忆感值(或忆感倒数值)一方面与磁通量φ有关,另一方面还与其内部变量ρ有关,两者交互影响.例如,一个简单的实际忆感器可用某种磁芯材料来实现,其忆感效应依赖于磁场的历史,即与磁通有关[10];除此之外还依赖于这种材料的某个参数,如磁场变化率、磁化率等.再如某些绝缘材料也有忆感器的效应[14].另外忆感效应还可通过改变电感的匝数和形状来实现,如文献[30]引入了一个类似滑动变阻器的忆感器模型,此模型中忆感器的中间滑动头到任一端的距离即是一个内部状态变量,显然其忆感或忆感倒数值与这个变量相关.
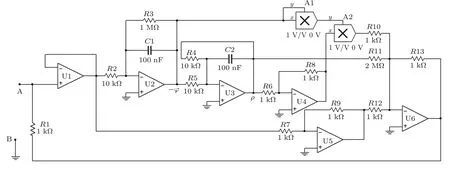
图1 忆感器的等效电路Fig.1.Equivalent circuit of the meminductor.
为了进一步研究此忆感器,利用Multisim软件建立了如图1所示的等效电路.若输入端AB接输入电压v,由等效电路可得:
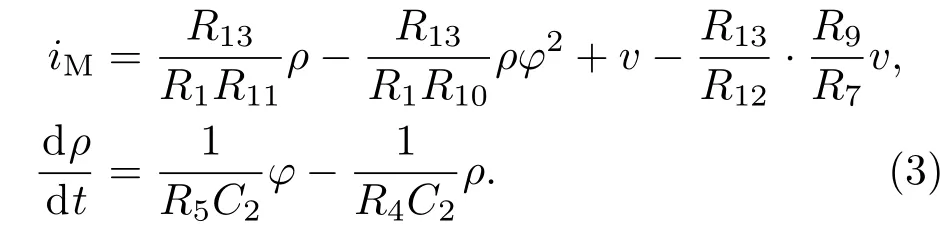
由于电路中的R7=R9,R12=R13,则(3)式简化为

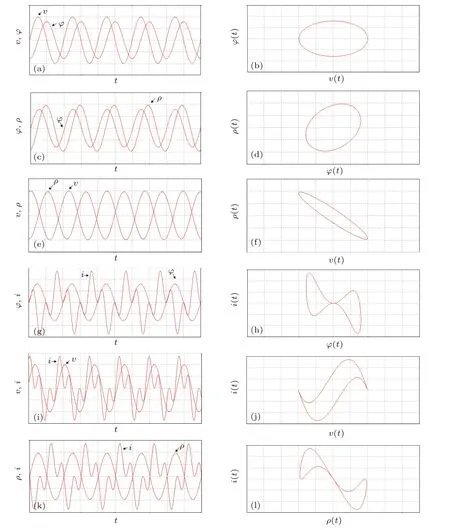
图2 电路的电压、电流、磁通量、状态变量测试结果 (a)v(t)和φ(t)的波形;(b)v-φ特性曲线;(c)φ(t)和ρ(t)的波形;(d)φ-ρ特性曲线;(e)v(t)和ρ(t)的波形;(f)v-ρ特性曲线;(g)φ(t)和i(t)的波形;(h)φ-i特性曲线;(i)v(t)和i(t)的波形;(j)v-i特性曲线;(k)ρ(t)和i(t)的波形;(l)ρ-i特性曲线Fig.2.Test results of voltage,current,magnetic flux and state variable of the circuit:(a)Time-domain waveforms ofv(t)andφ(t);(b)characteristic curve ofv-φ;(c)time-domain waveforms ofφ(t)andρ(t);(d)characteristic curve ofφ-ρ;(e)time-domain waveforms ofv(t)andρ(t);(f)characteristic curve ofv-ρ;(g)time-domain waveforms ofφ(t)andi(t);(h)characteristic curve ofφ-i;(i)time-domain waveforms ofv(t)andi(t);(j)characteristic curve ofv-i;(k)time-domain waveforms ofρ(t)andi(t);(l)characteristic curve ofρ-i.

图3 忆感器的φ-i特性图 (a)f=500 Hz;(b)f=600 Hz;(c)f=700 Hz;(d)f=800 HzFig.3.φ-ihysteresis loop of the meminductor in conditions of(a)f=500 Hz;(b)f=600 Hz;(c)f=700 Hz;(d)f=800 Hz.
3 忆感器文氏电桥混沌系统
3.1 忆感器文氏电桥混沌系统模型
下面利用(2)式所述的忆感器,建立如图4所示的忆感器文氏电桥混沌振荡器.根据基尔霍夫定律、电桥特性和元件特性关系,可得如下的电路的动态方程:


则方程(5)可变换为:
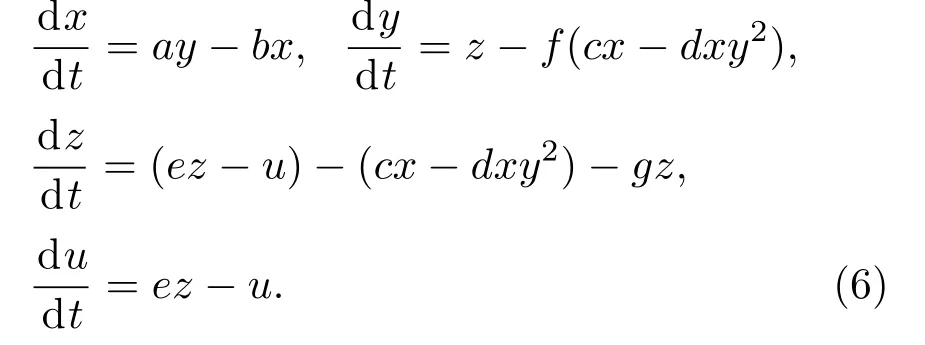
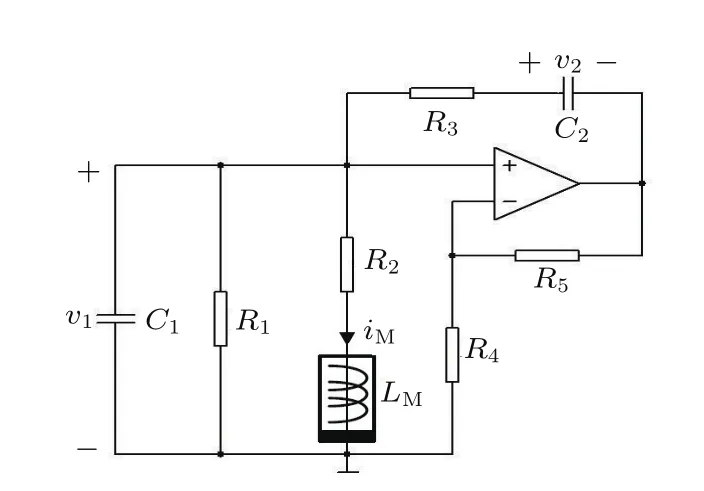
图4 忆感器文氏电桥混沌系统模型Fig.4. Model of the meminductive Wein-bridge chaotic system.

图5 忆感器文氏电桥混沌系统的时域波形Fig.5.Time-domain waveforms of the meminductive Wein-bridge chaotic system.

图6 忆感器文氏电桥混沌系统的混沌吸引子 (a)x-y平面相图;(b)y-z平面相图;(c)z-u平面相图;(d)u-x平面相图Fig.6.Chaotic attractors of the meminductive Wein-bridge chaotic system:(a)x-yphase diagram;(b)y-zphase diagram;(c)z-uphase diagram;(d)u-xphase diagram.
当参数选择为a=1.55,b=1,c=0.25,d=0.05,e=1,f=1,g=0.5时,在初始条件为(1,0,0.5,-0.5)的情况下,通过计算,可得Lyapunov指数为LE1=0.066,LE2=0,LE3=-0.531,LE4=-0.737,Lyapunov维数为DL=2.124,说明了系统处于混沌状态.此时,系统的时域波形如图5所示,系统的相平面上的投影如图6所示,在z=0截面上做的Poincaré映射如图7所示,这些结果可进一步说明此时系统的动力学行为是混沌的.

图7 忆感器文氏电桥混沌系统在z=0截面上的Poincaré 映射Fig.7.Poincaré mapping of the meminductive Weinbridge chaotic system onz=0 section.
3.2 系统的特性分析
3.2.1 平衡特性
若系统(6)是混沌系统,必须满足

因此,系统(6)在满足xy<(1+b-e)/2df的条件下为混沌系统.
由于系统(6)满足在(x,y,z,u)→(-x,-y,-z,-u)的变换下保持不变,因此,系统关于原点对称.
由(6)式的左边为零,可得

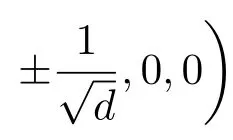

将参数a=1.55,b=1,c=0.25,d=0.05,e=1,f=1,g=0.5,代入(9)式,求得平衡点S0处的特征值为λ1,2=0.044±j0.851,λ3,4=-0.794±j0.414,故平衡点S0是不稳定的焦点.两个对称非零平衡点S±处的特征值为λ1=4.182,λ2=-1.252,λ3,4=0.665±j0.883,故平衡点S±是不稳定的鞍焦点.
3.2.2 系统参数对系统动力学的影响分析
随着系统参数的改变,系统的平衡点会发生变化,系统的稳定性将会发生变化,系统的状态也会发生变化.在初始条件(1,0,0.5,-0.5)下,固定参数b=1,c=0.25,d=0.05,e=1,f=1,g=0.5,改变a.当a在[1.52,1.5549]范围内变化时,系统Lyapunov的指数谱和分岔图如图8所示,为了更好地观察,图中将最小的Lyapunov指数忽略(下面的Lyapunov指数谱也进行同样处理).由图8可见,系统的Lyapunov指数谱与分岔图基本一致.系统的分岔形式为倍周期分岔,系统刚开始LE1=0,处于周期态或拟周期态,随着a的增大,系统的状态发生了变化,当LE1>0,系统的状态为混沌态,但是在混沌态的区域又有周期窗,系统状态呈现了复杂的变化过程.
同样,参数b也会影响系统状态.在同样的初始条件下,让参数a=1.55,c=0.25,d=0.05,e=1,f=1,g=0.5不变,让b在[0.998,1.02]范围内变化,得到的Lyapunov指数的系统Lyapunov指数谱和分岔图如图9(a)和图9(b)所示,两者基本符合.从图9可以看到,系统参数b变化过程中也存在周期、倍周期分岔、混沌和周期窗等复杂的非线性变化过程.
为了进一步认识参数a,b同时对系统状态影响的情况,让a在[1.535,1.558]范围和b在[0.995,1.008]范围内变化,绘制出如图10所示的动力学地图,图中黄色区域表示系统处于周期或准周期状态;蓝色区域表示系统处于混沌状态,褐色区域表示系统发散.由图10可见,随着a的增加和b的减少,系统的状态由周期态转变为混沌态,最后为发散状态.

图8 (网刊彩色)参数a变化的Lyapunov指数谱和分岔图 (a)参数a变化的Lyapunov指数谱;(b)参数a变化的分岔图Fig.8.(color online)Lyapunov spectrum and bifurcation diagram with respect toa:(a)Lyapunov spectrum;(b)bifurcation diagram.

图9 (网刊彩色)参数b变化的Lyapunov指数谱和分岔图 (a)参数b变化的Lyapunov指数谱;(b)参数b变化的分岔图Fig.9.(color online)Lyapunov spectrum and bifurcation diagram with respect tob:(a)Lyapunov spectrum and(b)bifurcation diagram.

图10 (网刊彩色)参数a和b的动力学地图Fig.10.(color online)Dynamical map withaandb.
3.2.3 恒Lyapunov指数谱特性
在初始条件(1,0,0.5,-0.5)下,固定参数a=1.55,b=1,c=0.25,e=1,f=1,g=0.5,改变d.当d在[0.005,0.1372]范围内变化时,系统Lyapunov指数谱和分岔图如图11所示.
在此区间系统处于恒定混沌状态,且呈现恒定Lyapunov指数现象.与其他忆阻器或忆感器振荡器相比,这是该忆感器文氏电桥振荡器非常重要的一种特性.适合作为秘钥进行信息加密的混沌系统应是鲁棒混沌或至少是结构稳定的混沌,该忆感器系统在参数扰动下具有恒定混沌与恒定Lyapunov指数特性,意味着其具有强鲁棒性和结构稳定性,因而适合于作为随机信号源,产生性能良好的伪随机序列.其他混沌系统一般在其混沌区间都存在周期窗口,当系统参数存在扰动驱使系统运动到周期轨道时,扰动下的映射与原混沌映射不是拓扑等价的,因而不是鲁棒的混沌映射.而该忆感器系统在其混沌参数区间无论参数d如何变化,始终维持恒定Lyapunov指数的恒定混沌振荡,这说明系统不因参数d的扰动或微小变化而使其由原来的混沌态进入到非拓扑等价的周期态.

图11 (网刊彩色)参数d变化的Lyapunov指数谱和分岔图 (a)参数d变化的Lyapunov指数谱;(b)Xmax-d分岔图Fig.11.(color online)Lyapunov spectrum and bifurcation diagram with respect tod:(a)Lyapunov spectrum;(b)bifurcation diagram.
全局非线性调幅是该忆感器文氏电桥振荡器的另一重要特性.从图11(b)看出,随着参数d的增加,混沌振荡信号x(或y,z,u)的幅值随参数d非线性变化,即幅值是参数的非线性函数.这种特性对混沌密码设计的最大优势在于大大提高了依据混沌振荡幅度预测系统参数从而重构混沌系统的安全性.一些著名的混沌系统如Logistic映射,在其混沌区间不但存在众多周期窗口,且其迭代幅值随参数线性变化,这大大降低了其作为密码的鲁棒性和安全性.
3.2.4 共存分岔模式
对于系统(6),在a=0.48,b=1,d=4,e=1,f=2.7,g=0.2不变的情况下,让参数c从1.45变化到1.66,对于不同初值(0.03,0,0.01,-0.01)和(-0.01,0.02,0.01,0.01),得到的Lyapunov指数谱和分岔图如图12所示,其中图12(a)和图12(b)是初值为(0.03,0,0.01,-0.01)的Lyapunov指数谱和分岔图,而图12(c)和图12(d)是初值为(-0.01,0.02,0.01,0.01)的Lyapunov指数谱和分岔图,图12(e)是两个不同初值的分岔图.由图12(a)-图12(d)可以看到,在相同初值情况下Lyapunov指数谱和分岔图一致.但是,从图12(a)和图12(c)看到,不同初值的情况下,系统的Lyapunov指数谱不完全一致,参数c∈[0.1601,0.1602]期间,初值为(0.03,0,0.01,-0.01)情况下LE1>0,而初值为(-0.01,0.02,0.01,0.01)情况下LE1<0.
同样地,在不同初值的情况下,系统的分岔图不一致,从图12(b)和图12(d)看到,初值为(0.03,0,0.01,-0.01)情况下的分岔图有一次跳跃,而初值为(-0.01,0.02,0.01,0.01)情况下的分岔图有两次跳跃.从图12(e)清楚地看到,存在共存分岔模式现象,随着参数c的增加,从一个稳定的周期轨道演变成上下两条稳定的周期轨道;经一次倍周期后,两者合在一起进行二次倍周期、多次倍周期分岔道路进入混沌轨道,共存分岔模式现象第一次消失;这之后,又分开为两条独立的混沌带;然后,随着混沌带的扩展,合并成一个大的混沌带,共存分岔模式现象最终彻底消失,在这个大的混沌带里存在着多个大小不一的多个周期窗.
3.2.5 吸引子的共存与重合
系统在取a=0.48,b=1,d=4,e=1,f=2.7,g=0.2,初值为(0.03,0,0.01,-0.01)和(-0.01,0.02,0.01,0.01)时,让c从0.145到0.166之间变化,会出现吸引子共存的现象.为了便于观察,初值为(0.03,0,0.01,-0.01)和(-0.01,0.02,0.01,0.01)的吸引子分别用红色和蓝色表示.当c在[0.1491,0.1592]区间内,出现了吸引子共存,吸引子为周期或拟周期的吸引子;在c=0.15时,共存的拟周期吸引子如图13(b)所示;在c=0.158时,共存的周期吸引子如图13(d)所示;并且,随着c的变化,两个吸引子的距离会发生变化.在c取值在[0.1608,0.1612]区间,出现了混沌吸引子共存,在c=0.1608时,共存的混沌吸引子如图13(e)所示.c为其他值时,吸引子共存现象消失,当c=0.146时,一般的周期吸引子如图13(a)所示;在c=0.16时,一般的拟周期吸引子如图13(d)所示;在c=0.164时,一般的混沌吸引子如图13(f)所示.当c≥0.1662时,系统发生发散现象.若将吸引子共存视为两个吸引子分开,吸引子共存消失视为两个吸引子重合,实际上,此期间是两个吸引子重合、分开、重合、分开、重合的过程.并且,吸引子的共存与重合与图12的共存分岔相符合.

图12 (网刊彩色)不同初值下的参数c的Lyapunov指数谱和分岔图 (a)初值为(0.03,0,0.01,-0.01)的Lyapunov指数谱;(b)初值为(0.03,0,0.01,-0.01)的分岔图;(c)初值为(-0.01,0.02,0.01,0.01)的Lyapunov指数谱;(d)初值为(-0.01,0.02,0.01,0.01)的分岔图;(e)两个不同初值的分岔图Fig.12.(color online)Bifurcation diagram and Lyapunov spectrum with respect tocunder different initial conditions:(a)Lyapunov spectrum and(b)bifurcation diagram under the initial conditions of(0.03,0,0.01,-0.01);(c)Lyapunov spectrum and(d)bifurcation diagram under the initial conditions of(-0.01,0.02,0.01,0.01);(e)bifurcation diagram of two different initial conditions.
通过以上共存分岔和共存吸引子的分析,可得如下结论.
1)所谓共存分岔或共存吸引子,实际是一种共存振荡,是指系统参数不变而仅初值变化时所引起的不同振荡状态变化的特性.即系统参数恒定时,初值变化可使其转换到不同的运动状态,可从一混沌吸引子转换到另一拓扑结构不同的混沌吸引子,即多个混沌吸引子共存.类似可有周期吸引子共存、混沌-周期吸引子共存等.
2)共存振荡反映了系统更高的初值敏感性.一般的混沌初值敏感性是指混沌运动轨迹(或混沌振荡信号)对不同的初值具有高度敏感性,即系统参数不变时,不同的初值产生完全不同的混沌轨迹.此时尽管混沌轨迹不同,但大都存在于一个相同拓扑结构的混沌吸引子之中,或运动轨迹随初值在同一吸引子之中跳跃.而在共存振荡中,不但运动轨迹在同一结构的混沌吸引子之中对初值敏感,对不同结构的混沌吸引子,不同结构的周期吸引子也极其敏感.即初值变化时,其运动轨迹不但在同一吸引子中跳跃,可从一个混沌吸引子跳跃到另一混沌吸引子,还可从周期吸引子跳跃到混沌吸引子,也可从一周期吸引子跳到另一周期吸引子.
3)共存振荡现象可存在多种实际应用.例如,根据共存混沌吸引子现象,可以把一个混沌系统设计为多个伪随机信号源,每个信号源对应于一个不同初值的混沌吸引子;再如,根据混沌-周期吸引子共存或周期-混沌吸引子共存现象进行混沌控制与反控制,混沌控制可以消除系统的混沌振荡,使其工作于非混沌状态,而混沌反控制可使系统由周期转换为混沌.

图13 (网刊彩色)共存吸引子与常规吸引子 (a)c=0.146;(b)c=0.1495;(c)c=0.158;(d)c=0.16;(e)c=0.1608;(f)c=0.164Fig.13.(color online)Coexisting attractor or conventional attractor of the system when(a)c=0.146;(b)c=0.1495;(c)c=0.158;(d)c=0.16;(e)c=0.1608;(f)c=0.164.
4 电路设计与实验验证
混沌系统可由电路来物理实现,电路实现时需要考虑时间常数的选择.时间常数会影响混沌信号在时域变化的快慢以及混沌信号频谱的分布范围,常被称为时间尺度变化因子,为了便于观察,选择合适的时间尺度变换因子尤为重要.因此,对(6)式引入时间尺度变换因子K,若取a=1.55,b=1,c=0.25,d=0.05,e=1,f=1,g=0.5,则(6)式改写为:
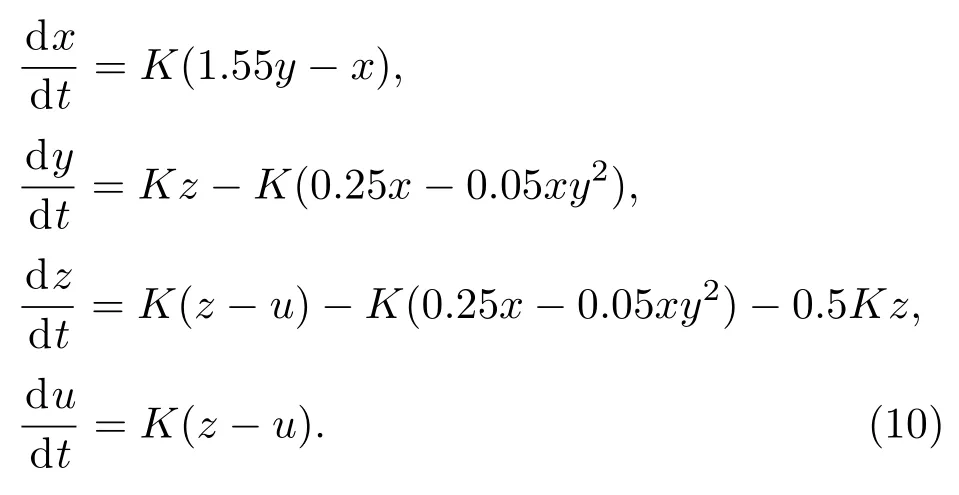
若用等效电路替代图4中的忆感器,将时间尺度变换因子取为K=10000,所有电容取为10 nF,根据(10)式便可建立如图14所示的忆感器文氏电桥混沌系统的电路,电路中的乘法器A1和A2由集成电路AD633来实现,其他元件的取值如图14所示.电路的实验结果如图15所示,其结果与图6中数值仿真的结果基本一致,证实了理论分析的正确性.

图14 忆感器文氏电桥混沌系统实现的电路原理图Fig.14.The circuit schematic of realizing the meminductive Wein-bridge chaotic system.
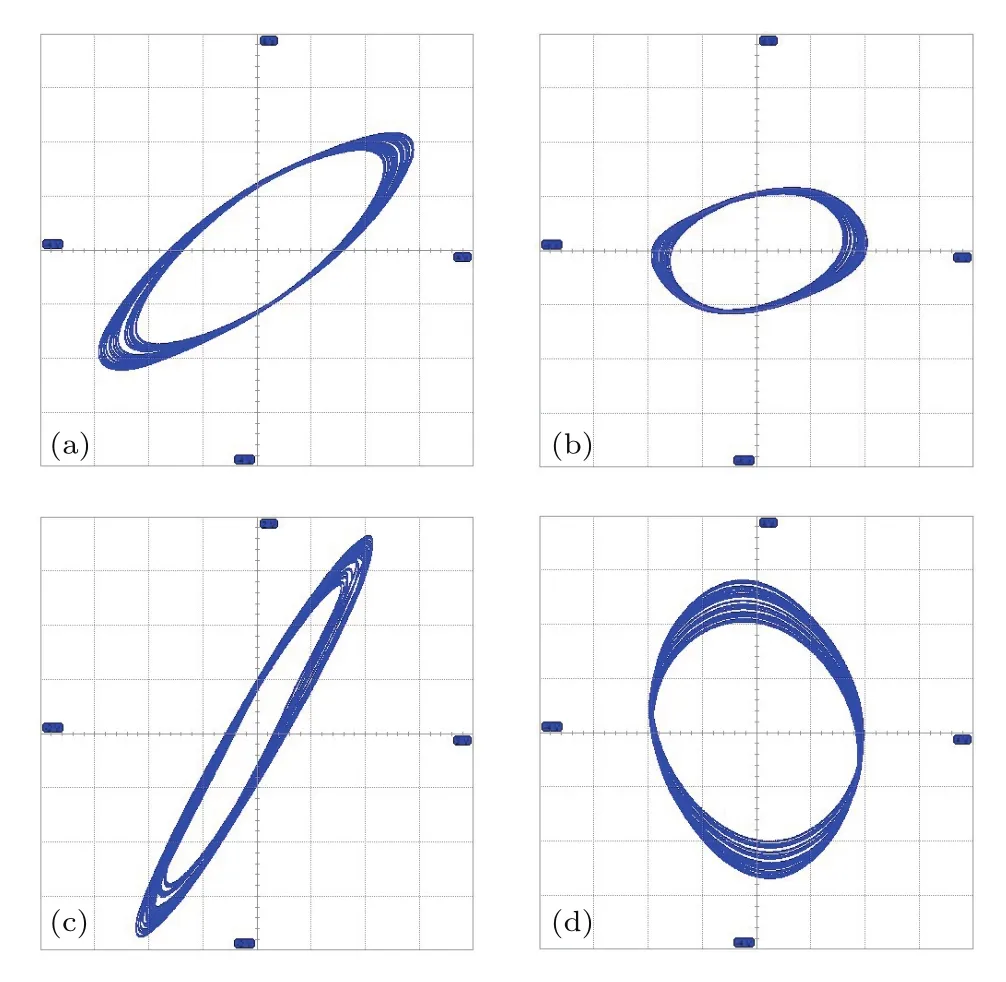
图15 实验中由示波器测量得到的混沌吸引子 (a)x-y平面相图;(b)y-z平面相图;(c)z-u平面相图;(d)u-x平面相图Fig.15.Experiment results of chaotic oscillator:(a)xyphase diagram;(b)y-zphase diagram;(c)z-uphase diagram;(d)u-xphase diagram.
5 结 论
本文针对目前忆感器内部状态量对时间的导数是磁通量的情况,拓展其物理概念,提出了一种新的忆感器数学模型,建立了等效电路,检测了电路的电压、电流、磁通量、状态变量的关系,分析其φ-i特性,发现与常见的忆感器模型一样,呈现紧致的滞回曲线.在此忆感器模型基础上,构造了忆感器文氏电桥混沌系统,并分析其非线性特性,分析发现此系统与其他混沌系统相比,不仅具有体现很好鲁棒性的恒Lyapunov指数谱、全局非线性调幅,还有极强初值敏感性的共存分岔模式和吸引子共存等复杂的非线性现象,这是少见的现象.文献[26,31]中混沌系统虽然出现了共存分岔模式和吸引子共存,但没出现恒Lyapunov指数谱、全局非线性调幅;文献[32,33]中混沌系统虽然出现了恒Lyapunov指数谱、全局非线性调幅,但没出现共存分岔模式和吸引子共存现象.电路实验验证了混沌现象的存在,证实了理论分析的正确性.由于此文氏电桥忆感器混沌系统不含电感元件,便于集成,并且兼具恒Lyapunov指数、全局非线性调幅、共存分岔模式和吸引子共存等现象,因此该系统具有良好的潜在应用价值,可作为多码源伪随数发生器,同时产生多路强鲁棒性的伪随机序列而应用于混沌密码和保密通信之中.
[1]Chua L O 1971IEEE Trans.Circuit Theory18 507
[2]Tour J M,He T 2008Nature453 42
[3]Strukov D B,Snider G S,Stewart D R,Williams R S 2008Nature453 80
[4]Mostafa H,Ismail Y 2016IEEE Trans.Semicond.Manuf.29 145
[5]Bass O,Fish A,Naveh D 2015Radioengineering24 425
[6]Duan S K,Hu X F,Dong Z K,Wang L D,Mazumder P 2015IEEE Trans.Neural Networks Learn.Syst.26 1202
[7]Wang L D,Duan M T,Duan S K,Hu X F 2014Sci.China:Inform.Sci.44 920(in Chinese)[王丽丹,段美涛,段书凯,胡小方2014中国科学:信息科学44 920]
[8]Semary M S,Malek H L A,Hassan H N,Radwan A G 2016Microelectron.J.51 58
[9]Yang X,Adeyemo A A,Jabir A,Mathew J 2016Electron.Lett.52 906
[10]Di Ventra M,Pershin Y V,Chua L O 2009Proc.IEEE97 1717
[11]Chua L O 1978Guest Lectures of the 1978 European Conference on Circuit Theory and Designp81
[12]Chua L O 2003Proc.IEEE91 1830
[13]Chua L O 2009 http://ieeexplore.ieee.org/xpl/modules abstract.jsp?mdnumber=EW1091[2016-08-01]
[14]Matsuo T,Okumura K,Kishima A 1999IEE Proc.-Circuits Devices Syst.146 176
[15]Han J H,Song C,Gao S,Wang Y Y,Chen C,Pan F 2014ACS Nano8 10043
[16]Pershin Y V,Di Ventra M 2010Electron.Lett.46 517
[17]Pershin Y V,Di Ventra M 2011Electron.Lett.47 243
[18]Liang Y,Yu D S,Chen H 2013Acta Phys.Sin.62 158501(in Chinese)[梁燕,于东升,陈昊 2013物理学报62 158501]
[19]Sah M P,Budhathoki R K,Yang C,Kim H 2014Circ.Syst.Signal Pr.33 2363
[20]Liang Y,Chen H,Yu D S 2014IEEE Trans.Circuits Syst.II61 299
[21]Biolek D,Biolek Z,Biolková V 2011Analog Integr.Circ.S.66 129
[22]Wang H,Wang X,Li C D,Chen L 2013Abstr.Appl.Anal.2013 281675
[23]Zheng C Y,Yu D S,Liang Y,Chen M K 2015Chin.Phys.B24 110701
[24]Yuan F,Wang G Y,Jin P P 2015Acta Phys.Sin.64 210504(in Chinese)[袁方,王光义,靳培培2015物理学报64 210504]
[25]Wang G Y,Jin P P,Wang X W,Shen Y R,Yuan F,Wang X Y 2016Chin.Phys.B25 090502
[26]Yu Q,Bao B C,Xu Q,Chen M,Hu W 2015Acta Phys.Sin.64 170503(in Chinese)[俞清,包伯成,徐权,陈墨,胡文2015物理学报64 170503]
[27]Li Z J,Zeng Y C 2014J.Electron.Inform.Technol.36 88(in Chinese)[李志军,曾以成2014电子与信息学报36 88]
[28]Yu J T,Li Y,Mu X M,Zhang J J,Miao X S,Wang S N 2015Radioengineering24 808
[29]Xu Z T,Jin K J,Gu L,Jin Y L,Ge C,Wang C,Guo H Z,Lu H B,Zhao R Q,Yang G Z 2012Small8 1279
[30]Shevchenko S N,van der Ploeg S H W,Grajcar M,Il’ichev E,Omelyanchouk A N,Meyer H G 2008Phys.Rev.B78 174527
[31]Chen M,Yu J J,Yu Q,Li C D,Bao B C 2014Entropy16 6464
[32]Deng W,Fang J,Wu Z J 2015Optik126 5468
[33]Li C B,Wang J,Hu W 2012Nonlinear Dyn.68 575
PACS:05.45.-a,05.45.Jn,05.45.Pq DOI:10.7498/aps.66.020502
Meminductive Wein-bridge chaotic oscillator∗
Xu Bi-Rong1)2)Wang Guang-Yi1)†
1)(Institute of Modern Circuits and Intelligent Information,Hangzhou Dianzi University,Hangzhou 310018,China)
2)(School of Mechanical and Electrical Engineering,Wuyi University,Wuyishan 354300,China)
29 July 2016;revised manuscript
5 November 2016)
A meminductor is a new type of memory device.It is of importance to study meminductor model and its application in nonlinear circuit prospectively.For this purpose,we present a novel mathematical model of meminductor,which considers the effects of internal state variable and therefore will be more consistent with future actual meminductor device.By using several operational amplifiers,multipliers,capacitors and resistors,the equivalent circuit of the model is designed for exploring its characteristics.This equivalent circuit can be employed to design meminductor-based application circuits as a meminductor emulator.By employing simulation experiment,we investigate the characteristics of this meminductor driven by sinusoidal excitation.The characteristic curves of current-flux(i-φ),voltage-flux(v-φ),v-ρ(internal variable of meminductor)andφ-ρfor the meminductor model are given by theoretical analyses and simulations.The curve of current-flux(i-φ)is a pinched hysteretic loop passing through the origin.The area bounding each sub-loop deforms as the frequency varies,and with the increase of frequency,the shape of the pinched hysteretic loop tends to be a straight line,indicating a dependence on frequency for the meminductor.Based on the meminductor model,a meminductive Wien-bridge chaotic oscillator is designed and analyzed.Some dynamical properties,including equilibrium points and the stability,bifurcation and Lyapunov exponent of the oscillator,are investigated in detail by theoretical analyses and simulations.By utilizing Lyapunov spectrum,bifurcation diagram and dynamical map,it is found that the system has periodic,quasi-periodic and chaotic states.Furthermore,there exist some complicated nonlinear phenomena for the system,such as constant Lyapunov exponent spectrum and nonlinear amplitude modulation of chaotic signals.Moreover,we also find the nonlinear phenomena of coexisting bifurcation and coexisting attractors,including coexistence of two different chaotic attractors and coexistence of two different periodic attractors.The phenomenon shows that the state of this oscilator is highly sensitive to its initial valuse,not only for chaotic state but also for periodic state,which is called coexistent oscillation in this paper.The basic mechanism and potential applications of the existing attractors are illustrated,which can be used to generate robust pseudo random sequence,or multiplexed pseudo random sequence.Finally,by using the equivalent circuit of the proposed meminducive model,we realize an analog electronic circuit of the meminductive Wien-bridge chaotic system.The results of circuit experiment are displayed by the oscilloscope,which can verify the chaotic characteristics of the oscillator.The oscillator,as a pseudo random signal source,can be used to generate chaotic signals for the applications in chaotic cryptography and secret communications.
meminductor,Wien bridge,chaos,coexisting attractor
:05.45.-a,05.45.Jn,05.45.Pq
10.7498/aps.66.020502
∗国家自然科学基金 (批准号:61271064,60971046,61401134)、浙江省自然科学基金 (批准号:LZ12F01001,LQ14F010008)、福建省自然科学基金(批准号:2016J01761)和浙江省重点科技创新团队(批准号:2010R50010)资助的课题.
†通信作者.E-mail:wanggyi@163.com
*Project supported by the National Natural Science Foundation of China(Grant Nos.61271064,60971046,61401134),the Natural Science Foundations of Zhejiang Province,China(Grant Nos.LZ12F01001,LQ14F010008),the Natural Science Foundations of Fujian Province,China(Grant No.2016J01761),and the Program for Zhejiang Leading Team of S&T Innovation,China(Grant No.2010R50010).
†Corresponding author.E-mail:wanggyi@163.com

