余维-1非光滑分岔下的簇发振荡及其机理∗
张正娣 刘杨 张苏珍 毕勤胜
(江苏大学理学院,镇江 212013)
余维-1非光滑分岔下的簇发振荡及其机理∗
张正娣 刘杨 张苏珍 毕勤胜†
(江苏大学理学院,镇江 212013)
(2016年8月15日收到;2016年11月2日收到修改稿)
不同尺度耦合会导致一些特殊的振荡行为,通常表现为大幅振荡与微幅振荡的组合,也即所谓的簇发振荡.迄今为止,相关工作大都是围绕光滑系统开展的,而非光滑系统中由于存在着各种形式的非常规分岔,从而可能会导致更为复杂的簇发振荡模式.本文旨在揭示存在非光滑分岔时动力系统的不同尺度耦合效应.以典型的含两个非光滑分界面的广义蔡氏电路为例,通过引入周期变化的电流源以及一个用于控制的电容,选取适当的参数使得周期频率与系统频率之间存在量级差距,建立了含不同尺度的四维分段线性动力系统模型.基于快子系统在不同区域中的平衡点及其稳定性分析,以及系统轨迹穿越非光滑分界面时的分岔分析,得到了不同余维非光滑分岔的存在条件及其分岔行为.重点探讨了余维-1非光滑分岔下的簇发振荡的吸引子结构及其产生机理,揭示了非光滑分岔下系统复杂振荡行为的本质.
非光滑电路系统,不同尺度,簇发振荡,非常规分岔
1 引 言
在实际工程系统中往往存在大量非光滑因素,如碰撞[1]、干摩擦[2]、开关[3]、脉冲控制[4]等.根据所建立的数学模型中的非光滑度的不同,非光滑系统大致可以分为以下三类:1)非光滑连续系统,系统的向量场连续,而其Jacobi矩阵不连续,如蔡氏电路系统[5];2)Filippov系统,系统的向量场和其Jacobi矩阵均不连续,但其状态空间连续,如干摩擦系统[6];3)非光滑脉冲系统,系统的向量场、Jacobi矩阵及其状态空间均不连续,如碰撞系统[7].
与光滑系统相比,非光滑动力系统存在许多特殊的动力学现象,如丰富的运动形式、分岔行为及通向混沌路径的多样性[8].同时,由于系统的非光滑性,传统的分析分岔及复杂性的方法对非光滑系统不再适用,需要探索一些新的方法和手段[9],因此,非光滑系统动力学的理论分析、数值计算和应用研究具有一定的挑战性.
针对非光滑动力系统,国内外许多学者开展了一系列研究.例如,Shaw和Holmes[10]对低维情形下的冲击振子和分段线性振子系统展开了一系列研究,发现该类系统存在着次谐响应、倍周期分岔等非线性特征;Nordmark等[11]通过建立Poincaré-Nordmark映射,分析了冲击振子发生碰撞时的运动形式,发现其中存在着一种被称作擦边碰撞的现象,且在周期运动状态下的振子,通过擦边分岔可以直接进入混沌运动;Hu[12]针对分段光滑的系统,分析了向量场的非光滑性对Poincaré映射可微性的影响;Xu[13]探究了该类系统复杂动力学行为的产生机理;陆启韶和金俐[14]研究分析了在刚性约束下的n维非线性系统的动力学行为,建立了这一类型的系统在刚性约束附近具有的局部映射关系,给出了该系统局部映射Jacobi矩阵的计算方法;姜海波等[15]对脉冲作用下Chen系统进行了非光滑分岔分析,运用了Floquet理论揭示了系统周期解的分岔机理.
由于缺乏有效的分析手段,相关研究大都是围绕着平衡点或周期轨道展开的[16],并通过不同的数值方法建立其相应的分岔图,例如强制法,仅能给出稳定的周期轨道,又如轨道跟踪法,虽然能够给出相关的不稳定轨道,但仅能展现常规分岔模式.为解释非光滑分岔机理,以Leine为代表的学者引入微分包含理论来分析系统在非光滑分界面上的分岔特性[17],通过分析广义Jacobi矩阵的特征值随辅助参数的退化情况,揭示各种非光滑分岔的动力特性及其相应的产生机理.
迄今为止,相关工作大都是针对同一尺度下的非光滑系统的分岔展开的,基本上没有涉及不同尺度耦合下的非光滑动力系统的研究,而事实上,不同尺度耦合系统,涉及到科学和工程技术的各个领域.例如,飞行器中存在着快速的旋转运动与相对较慢的平动之间的耦合[18],绳系卫星中系绳的纵横向振动与卫星姿态动力学之间的耦合[19],催化反应中存在着不同量级的反应速率[20],而几乎所有的神经元模型几乎都包含不同尺度之间的耦合[21].
不同尺度耦合系统的研究最早可以追溯到Poincaré研究行星轨道时提出的奇异摄动方程,但是直到诺贝尔奖获得者Hodgkin和Huxley[22]建立了快慢两尺度神经元放电模型(H-H模型),成功地再现了其中的簇发放电行为,不同尺度耦合系统的复杂性才引起了学术界的高度重视.由于传统的非线性理论无法解决不同尺度之间的相互作用,早期相关工作大都局限在近似求解、数值仿真和实验分析.直到2000年,Izhikevich[23]引入了Rinzel的快慢分析法才将相关研究上升到机理分析的层次.虽然近年来在不同尺度耦合领域取得了一定的进展,但绝大部分结果均是针对光滑系统取得的,而非光滑系统由于存在着非光滑分岔,不仅会导致一些特殊的簇发振荡现象,也会使得相应的簇发振荡结果更加复杂.同时,针对时域上不同尺度耦合的工作开展较多,而频域上不同尺度耦合由于不存在明显的快慢子系统,相关工作开展较少.
自Chua和Lin[24]构建了存在混沌现象的蔡氏电路以来,其动力特性引起了国内外学者的广泛关注并开展了大量的研究[25,26].以原始的具有分段线性特性的蔡氏电路为基础,通过引起其他元器件或改变其中非线性阻尼的伏安特性,得到了各种形式的蔡氏电路,给出了许多典型的非线性现象,如倍周期分岔的混沌道路、多涡卷混沌吸引子等等[27,28].但是,相关工作均是在同一尺度上开展的,同时,很少考虑其中的非光滑分岔特性.本文旨在揭示存在非光滑分岔时系统频域上的不同尺度效应.以典型的含两个非光滑分界面的广义蔡氏电路为例,通过引入周期变化的电流源以及用于控制的电容,适当选择参数,使得激励频率远小于系统的固有频率,建立了含频域两尺度耦合的四维分段线性非光滑动力系统.讨论了非光滑分界面上的非常规分岔条件,分析了余维-1非光滑分岔下的簇发振荡及其产生机理.
2 数学模型
具有分段线性特性的蔡氏电路不仅在实验室容易搭建,而且存在着诸如概周期振荡、混沌振荡等复杂动力学行为,因此常被作为基础模型来研究各种非线性现象.本文在典型的非光滑广义蔡氏电路的基础上,引入控制电容C1和周期变化的电流源iG,如图1所示,其中包含两个电感L1和L2,两个电容C1和C2以及一个分段线性的非线性电阻RG,同时并联一个周期变化的电流源iG,其相应的动力学模型可以表示为

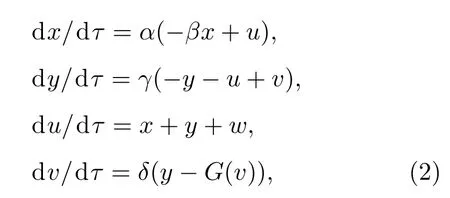

图1 电路原理图Fig.1.Circuit schematic diagram.
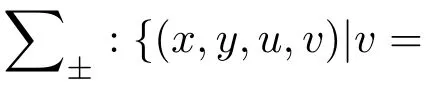
3 快子系统分岔分析
取定参数Ω=0.01,α=0.001,而其他参数为常规量,也即考虑在弱控制下系统激励频率与系统固有频率ω之间存在量级差距时其动力学行为. 显然,在固有频率对应的任一周期T∈[τ0,τ0+2π/ω]内, 外激励项w将在WA=Asin(Ωτ0)和WB=Asin(Ωτ0+2πΩ/ω)之间变化,由于Ω≪ω,WA≈WB,也即虽然外激励项会在±A之间变化,但在任一固有频率所对应的周期内,w变化非常缓慢,因此,整个外激励项w可视为慢变参数.因此快子系统可以表示为

而慢子系统则为

在区域D0中,快子系统具有如下惟一的平衡点E0:

而在区域D±中,快子系统分别存在惟一的平衡点E±:
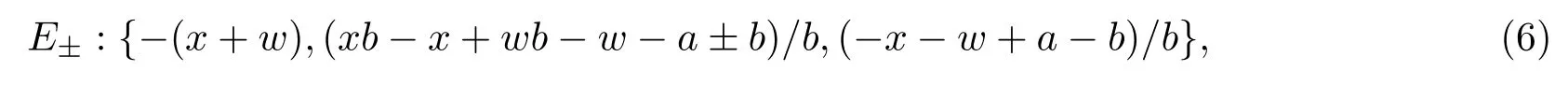


其中k1=γ+δb-qδb+qδa,k2=γ-δγ+δγbqδγb+qδγa,k3=-qδγb+qδγa+δγb. 系统中可能会产生两种不同形式的非光滑分岔,一是在分界面处发生fold分岔,其产生条件为

另一是在分界面处发生Hopf分岔,其产生条件为

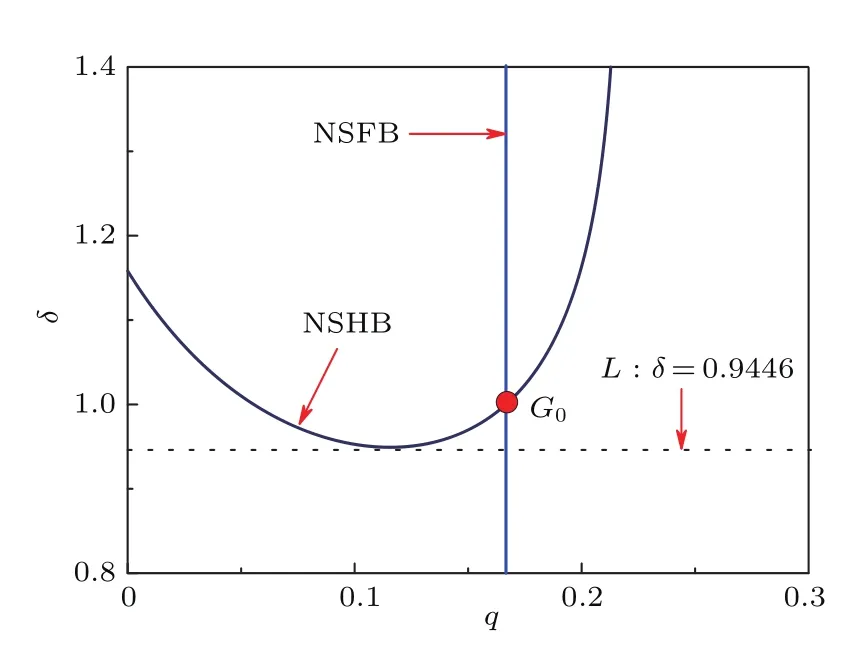
图2 (q,δ)平面上的非光滑分岔集Fig.2.The non-smooth bifurcation sets on the(q,δ)plane.
取定参数β=1.2,γ=0.6,a=-3.0,b=0.6,A=3.0,图2给出了(q,δ)平面上的非光滑分岔图,显然当δ<0.9446时,随着q在[0,1]之间变化,广义Jacobi矩阵存在零特征值,因此会产生余维-1非光滑fold分岔,而当δ>0.9446时,不仅会存在零特征值,也会存在一对纯虚根,因此存在二次穿越现象,导致余维-2非光滑fold-Hopf分岔.
4 非光滑余维-1周期簇发振荡
4.1 周期簇发振荡运动过程
由图2可知,当δ=0.9时,在分界面上仅会产生余维-1非光滑fold分岔,此时快子系统在三个不同区域中分别存在着三个不同的平衡点,计算可知,E0为不稳定鞍点,其相应的特征值为λ1=2.8476,λ2,3=-0.3738±0.6551I;E±为稳定焦点,其相应的特征值为λ1=-1.0651,λ2,3=-0.0375±0.5503I.图3给出了δ=0.9时系统在(y,v)和(u,v)平面上的相图.

图3δ=0.9时的相图 (a)(y,v)平面的相图;(b)(u,v)平面的相图Fig.3.Phase portraits forδ=0.9:(a)On the(y,v)plane;(b)on the(u,v)plane.
我们以(y,v)平面上的相图为例来说明轨迹的运动情况.假设轨迹从非光滑分界面v=+1上的A1点出发,由于在D+域内存在惟一的稳定焦点E+,此时轨迹将大致按照E+的特性,逐渐振荡趋于E+.在此过程中,由于外激励是一个慢变过程,因此系统轨迹主要由快子系统决定.当轨迹逼近于E+时,由于E+是稳定的焦点,快子系统只会使得系统轨迹驻留在E+点,因此慢变的外激励的影响将会体现出来.在外激励的作用下,其相应的平衡点E+的位置会发生变化,大致沿着E+A3向分界面移动,从而导致系统轨迹缓慢地由A2点运动到A3点.当轨迹到达分界面上的A3点,由于在D0域内存在惟一的不稳定鞍点,在慢变外激励驱动下,系统轨迹快速地穿越D0域,到达分界面v=-1上的A4点,并从A4点出发,逐渐振荡趋于D-区域中惟一稳定的焦点E-.经过与D+区域内相对称的过程,抵达分界面v=-1上的A6点,并快速穿越区域D0,到达起始点A1,完成一个周期的簇发振荡.
4.2 周期簇发振荡的结构
为进一步说明周期簇发振荡的结构,图4给出了其相应的时间历程.
从图3(a)中可以看出,在簇发振荡对称的半个周期内,大致包含三个部分:1)从分界面上A1点逐渐趋于E+的逼近过程;2)从E+附近向分界面上A3点的运动过程;3)从A3穿越区域D0到A4的过程.其中第二过程占据了主要部分.
第一过程对应于从A1到E+的逼近过程(见图4(c)),振荡频率主要受E+所对应的共轭复根的虚部的影响,通过计算,其振荡周期的理论值为TS=2π/0.5503=11.4177,这与图4(c)中的数值模拟值TP=11.4272相符合,其振荡幅值的变化主要受该对共轭复根的实部影响,其在v方向上的变化可以用曲线AP来描述,近似为VP=VP0exp[-0.0375(t-tP0)],其中VP0和tP0分别对应于在A1处围绕E+振荡在方向上的幅值和时间.从图4(c)可以看出曲线AP大致与从A1点到E+的振荡幅值符合,因此,按照振幅衰减到起始振幅的1%为标准,从A1点到E+时间的理论值可以计算为T1=122.80,这与图4(c)中的数值模拟值TP1=141.45也较为符合.
第二过程主要对应于随慢变量x的变化平衡点向分界面移动的过程,由于受外激励的影响,该过程从E+振荡趋于A3点,其振荡周期为TE=2π/Ω,这与图4(b)中的数值模拟结果一致,而振荡幅值主要受(3)式中的第一式所对应的特征值λT=0.0001(-β-1)=-0.00022的控制,其在v方向上随时间的变化大致可以用曲线AT来描述,其相应的表达式为VE=V0exp[-0.00022(t-t0)],其中v0和t0对应于轨迹在E+处的v值及所对应的时间,因此,可以从理论上计算从E+到A3点的时间为T2=ln(10.8761)/0.00022=10848.0.
第三过程对应于穿越区域D0的过程,由于时间非常短,可以忽略不计,通过计算可以得到簇发振荡周期的理论解为TJ=2(10848.0+122.80)=21941.6,与数值模拟结果T0=23140符合良好(见图4(a)).
4.3 簇发振荡机理分析
为揭示该簇发振荡的机理,在此采用包络分析法. 其主要思想是,分别考察外激励项w=Asin(Ωt)在w=±A极值处的平衡态及其分岔模式,并结合系统的相图,得到不同簇发振荡的产生机理.图5给出了在(x,v)平面上系统簇发振荡的相图与快子系统的包络平衡线的叠加图.

图5 (x,v)平面上簇发振荡相图与快子系统(x,v)平衡曲线的叠加图Fig.5.The overlap diagram between the phase portrait and the equilibrium branches of the fast subsystem on the(x,v)plane.
图5中B±分别对应于w=±A=±0.5时三个不同区域的快子系统的平衡线.假设系统轨迹从分界面v=+1上的A1点(见图3(a))出发,轨迹受D+区域内的系统控制,逐渐趋于D+区域内快子系统惟一稳定焦点E+,由于A1点与E+之间存在较大的距离,使得逼近过程存在大幅振荡特性,也即处于激发态并大致按照E+的特性,振幅逐渐减小,振荡趋于E+,进入沉寂态虽然此时快子系统的轨迹将稳定于E+,但耦合系统的轨迹由于受第二个尺度也即慢变周期激励的影响,将按照外激励周期做小幅周期振荡,也即开始激发态振荡.在该过程中,由于整个外激励值在±A之间周期变化,导致耦合系统在该阶段周期振荡的轨迹在分别取w=±A所得到的快子系统的两条平衡线之间来回变化,并受两条平衡线的制约,使得轨迹逐渐振荡趋于分界面v=+1.
当轨迹到达分界面v=+1上的A3点时,受平衡线的制约,轨迹将穿越分界面,而由于在D0域内存在惟一的不稳定鞍点,所以在慢变外激励驱动下,系统轨迹快速地穿越D0域,到达分界面v=-1上的A4点,形成沉寂态并从A4点出发,逐渐振荡趋于D-区域中惟一稳定的焦点E-.同样,由于A4点和E-之间存在着较大的距离,使得该逼近过程存在着较大幅值的振荡,导致激发态由于慢变激励项w按照外激励频率Ω在w=±A之间周期变化,导致轨迹也按照频率Ω在w=±A所对应的两条平衡线之间周期来回变化,直至轨迹到达分界面v=-1上的A6点,并快速穿越区域D0,到达起始点A1,完成一个周期的簇发振荡.
需要指出的是,由于D0区域中不稳定鞍点所对应的实特征值较大,使得轨迹会快速穿越D0区域,分别趋于D±中的稳定焦点,同时,当轨迹抵达D+或D-区域中w=±A时快子系统的两条平衡线之间时,振荡轨迹会在这两条平衡线之间来回周期振荡,也即轨迹为w=±A时快子系统的两条平衡线包络.
5 结 论
对于周期激励下含两非光滑分界面的广义蔡氏电路,选取适当的参数使得周期频率与系统频率之间存在量级差,建立了一个含频域两时间尺度的四维分段线性系统.通过对快子系统进行平衡点以及非光滑分岔分析可知,在具体参数下,当系统轨迹穿越非光滑分界面时,会产生余维-1非常规fold分岔,从而导致了簇发振荡现象的产生.这与光滑系统中的簇发振荡现象不同,光滑系统中轨迹是在系统同时存在的不同稳定平衡点之间跳跃,而在该非光滑系统中,轨迹是在不同区域中惟一的平衡点之间的跳跃,从而揭示了非光滑因素下非常规fold分岔对系统簇发振荡行为的影响机理.本文仅探讨了非光滑系统中的余维-1非常规fold分岔导致的簇发振荡,对于系统的更复杂的簇发振荡还有待进一步研究.
[1]Siefert A,Henkel F O 2014Nucl.Eng.Des.269 130
[2]Duan C,Singh R 2005J.Sound Vib.285 1223
[3]Zhusubaliyev Z H,Mosekilde E 2008Phys.Lett.A372 2237
[4]Jiang H B,Li T,Zeng X L,Zhang L P 2013Acta Phys.Sin.62 120508(in Chinese)[姜海波,李涛,曾小亮,张丽萍2013物理学报62 120508]
[5]Galvenetto U 2001J.Sound Vib.248 653
[6]Carmona V,Fernández-García S,Freire E 2012Physica D241 623
[7]Dercole F,Gragnani A,Rinaldi S 2007Theor.Popul.Biol.72 197
[8]Zhusubaliyev Z T,Mosekilde E 2008Physica D237 930
[9]Rene O,Baptista M S,Caldas I L 2003Physica D186 133
[10]Shaw S W,Holmes P A 1983J.Sound Vib.90 129
[11]Nordmark A,Dankowicz H,Champneys A 2009Int.J.Non-Linear Mech.44 1011
[12]Hu H Y 1995Chaos,Solitons Fractals5 2201
[13]Xu H D 2008Ph.D.Dissertation(Sichuan:Southwest Jiaotong University)(in Chinese)[徐慧东2008博士学位论文(四川:西南交通大学)]
[14]Lu Q S,Jin L 2005Acta Mech.Sol.Sin.26 132(in Chinese)[陆启韶,金俐 2005固体力学学报 26 132]
[15]Jiang H B,Zhang L P,Chen Z Y,Bi Q S 2012Acta Phys.Sin.61 080505(in Chinese)[姜海波,张丽萍,陈章耀,毕勤胜2012物理学报61 080505]
[16]Stavrinides S G,Deliolanis N C 2008Chaos,Solitons Fractals36 1055
[17]Leine R I 2006Physica D223 121
[18]Jia Z,Leimkuhler B 2003Future Gener.Comp.Syst.19 415
[19]Leimkuhler B 2002Appl.Numer.Math.43 175
[20]Gyorgy L,Field R J 1992Nature355 808
[21]Duan L X,Lu Q S,Wang Q Y 2008Neurocomputing72 341
[22]Hodgkin A L,Huxley A F 1952J.Physiol.117 500
[23]Izhikevich E M 2000Int.J.Bifurcation Chaos6 1171
[24]Chua L O,Lin G N 1990IEEE Trans.Circuits Syst.37 885
[25]Mkaouar H,Boubaker O 2012Commun.Nonlinear Sci.Numer.Simul.17 1292
[26]Kahan S,Sicardi-Schifino A C 1999Physica A262 144
[27]Baptist M S,Caldas I L 1999Physica D132 325
[28]Stavrinides S G,Deliolanis N C,Miliou A N,Laopoulos T,Anagnostopoulos A N 2008Chaos,Solitons Fractals36 1055
PACS:05.45.-a,05.45.Pq DOI:10.7498/aps.66.020501
Bursting oscillations as well as the mechanism with codimension-1 non-smooth bifurcation∗
Zhang Zheng-DiLiu Yang Zhang Su-Zhen Bi Qin-Sheng†
(Faculty of Science,Jiangsu University,Zhenjiang 212013,China)
15 August 2016;revised manuscript
2 November 2016)
The coupling of different scales in nonlinear systems may lead to some special dynamical phenomena,which always behaves in the combination between large-amplitude oscillations and small-amplitude oscillations,namely bursting oscillations.Up to now,most of therelevant reports have focused on the smooth dynamical systems.However,the coupling of different scales in non-smooth systems may lead to more complicated forms of bursting oscillations because of the existences of different types of non-conventional bifurcations in non-smooth systems.The main purpose of the paper is to explore the coupling effects of multiple scales in non-smooth dynamical systems with non-conventional bifurcations which may occur at the non-smooth boundaries.According to the typical generalized Chua’s electrical circuit which contains two non-smooth boundaries,we establish a four-dimensional piecewise-linear dynamical model with different scales in frequency domain.In the model,we introduce a periodically changed current source as well as a capacity for controlling.We select suitable parameter values such that an order gap exists between the exciting frequency and the natural frequency.The state space is divided into several regions in which different types of equilibrium points of the fast sub-system can be observed.By employing the generalized Clarke derivative,different forms of non-smooth bifurcations as well as the conditions are derived when the trajectory passes across the non-smooth boundaries.The case of codimension-1 non-conventional bifurcation is taken for example to investigate the effects of multiple scales on the dynamics of the system.Periodic bursting oscillations can be observed in which codimension-1 bifurcation causes the transitions between the quiescent states and the spiking states.The structure analysis of the attractor points out that the trajectory can be divided into three segments located in different regions.The theoretical period of the movement as well as the amplitudes of the spiking oscillations is derived accordingly,which agrees well with the numerical result.Based on the envelope analysis,the mechanism of the bursting oscillations is presented,which reveals the characteristics of the quiescent states and the repetitive spiking oscillations.Furthermore,unlike the fold bifurcations which may lead to jumping phenomena between two different equilibrium points of the system,the non-smooth fold bifurcation may cause the jumping phenomenon between two equilibrium points located in two regions divided by the non-smooth boundaries.When the trajectory of the system passes across the non-smooth boundaries,non-smooth fold bifurcations may cause the system to tend to different equilibrium points,corresponding to the transitions between quiescent states and spiking states,which may lead to the bursting oscillations.
non-smooth circuit system,multiple scales,bursting oscillations,non-conventional bifurcation
:05.45.-a,05.45.Pq
10.7498/aps.66.020501
∗国家自然科学基金(批准号:11472115,11472116)和江苏省青蓝工程资助的课题.
†通信作者.E-mail:qbi@ujs.edu.cn.
*Project supported by the National Natural Science Foundation of China(Grant Nos.11472115,11472116)and the Qinglan Project of Jiangsu Province,China.
†Corresponding author.E-mail:qbi@ujs.edu.cn.

