三次型蔡氏电路的设计及应用*

吕恩胜

(河南应用技术职业学院机电工程学院，河南 郑州 450042)

Chua L O 于1983 年提出了著名的经典蔡氏电路(Chua’s circuit)，其动力学行为丰富，取得了广泛的应用，成为混沌科学研究的热点对象[1-2]。蔡氏电路最核心之处是蔡氏二极管，其结构复杂，因此物理实现存在着较多的困难。诸多学者对蔡氏二极管的硬件电路设计给予了研究:文献[3]采用标度化技术[4]设计了两类无感蔡氏电路；文献[5]对蔡氏二极管的设计提出了用分段线性正电阻的设计方法；文献[6-8]采用忆阻器替代蔡氏二极管的方法设计了蔡氏电路；文献[9]设计了分数阶蔡氏电路。上述采用标度化技术的方法符合工程规范，但不遵循蔡氏电路方程；分段线性电阻设计方法，改进后的电路还保留电感，这对集成电路大规模实现还存在挑战；忆阻器、分数阶蔡氏电路，还只是在理论层面上的设计，目前还没有实际可行的硬件电路。尽管蔡氏电路经过近40 年的研究，设计出的各种电路仍然不够完善，还存在各种问题。

针对上述的改进方法和出现的问题，在遵循电路方程和参数的基础上，设计易于用普通电子元件实现大规模集成的蔡氏电路方案。本文在研究蔡氏电路方程后，对非线性单元函数的元素重新归类，根据新的非线性函数特性曲线，提出3 类三次型非线性函数，设计了功能全同和拓扑等效的两类蔡氏电路，方程简练，硬件调试方便，适用于混沌保密通信，为大规模集成实现提供了理论及技术基础。

1 蔡氏电路方程

蔡氏电路是混沌领域工作者取得的第一个物理成果，它开创了混沌电路的新纪元，得到了广泛的研究，归一化方程为

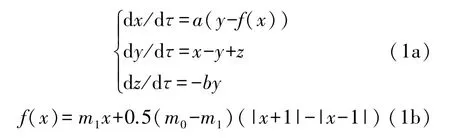
f(x)为系统函数的非线性单元，即蔡氏二极管，其中m0=-1/7、m1=2/7，a、b为参数，典型值分别为:10、15。

2 三次型非线性函数设计

2.1 饱和特性函数的设计

蔡氏电路的实现，关键是非线性单元的电路设计，将式(1b)的m1x部分归为线性项，式(1a)改为dx/dτ=a(y-m1x-f′(x))，改进的式(1b)为

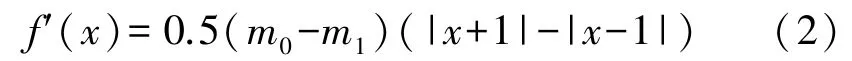
不考虑m0、m1情况下，式(2)表示的蔡氏二极管的核心部分写为: 0.5(｜x+1 ｜-｜x-1 ｜)，是一种具有饱和特性的函数，也可写为式(3)，f′(x)=(m1-m0)h(x)，式(3)的波形是分段线性的三折曲线，如图1 所示。

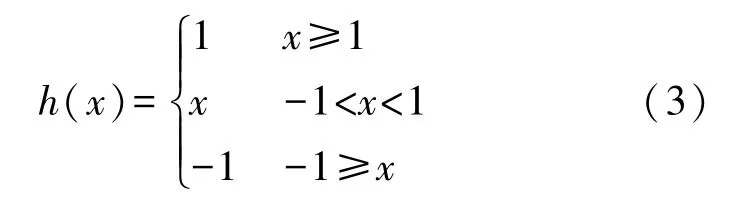
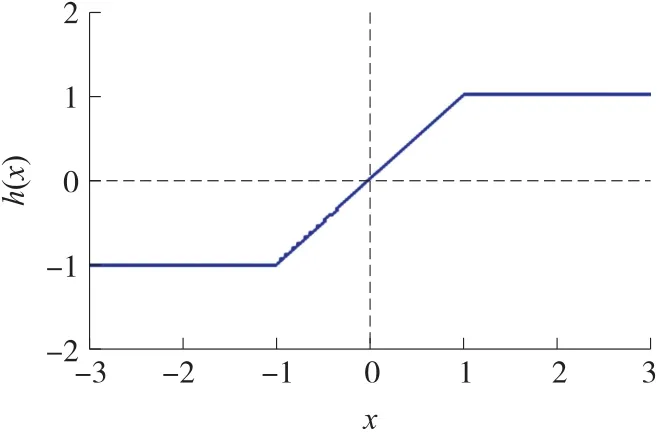
图1 饱和函数特性曲线

2.2 三次型函数的设计与分析

图1 所示的h(x)曲线，与最高次为x3的多项式函数曲线局部相似，中斜外平，这类函数统称为三次型，文献[10]利用集成运放的限幅特性来实现，本文提出的与图1 近似的三次型曲线有:三次方函数曲线、Logistic 函数曲线、反向并联二极管伏安曲线，如图2 所示，与之对应的函数为式(4)、(5)、(7)。

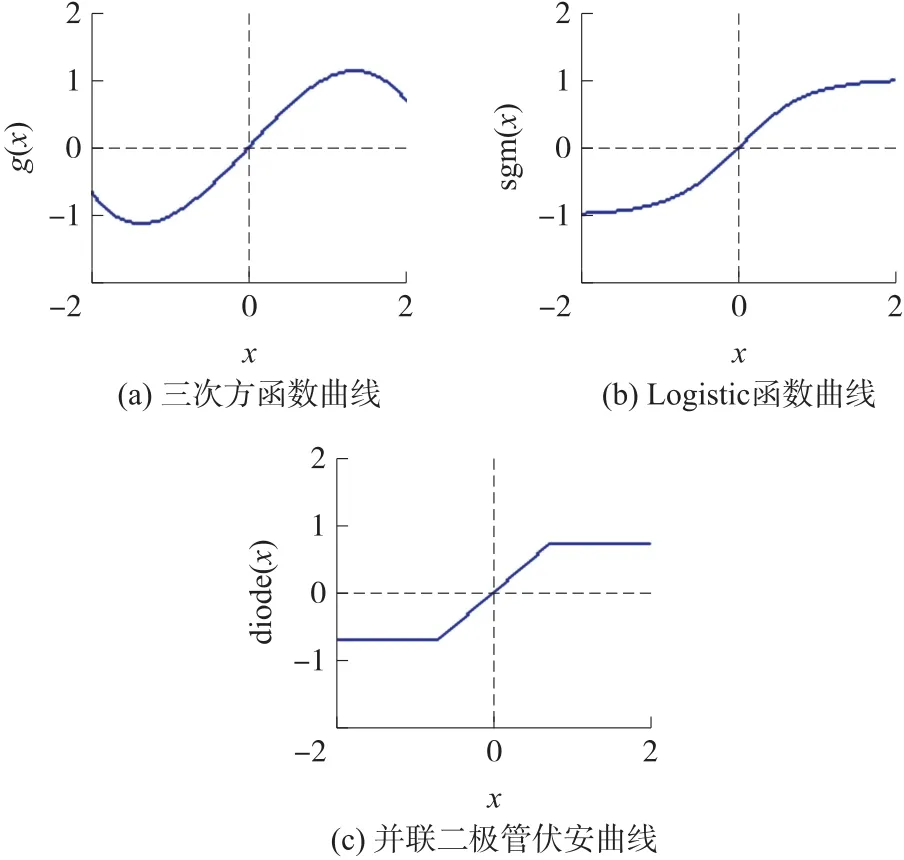
图2 三次型函数特性曲线

三次方函数

Logistic 函数

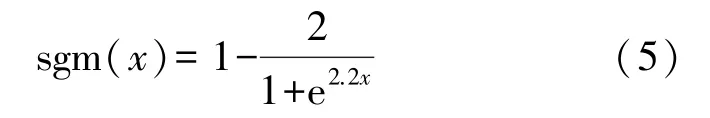
sgm(x)由sigmoid(x)函数变换而来，起源于生物学

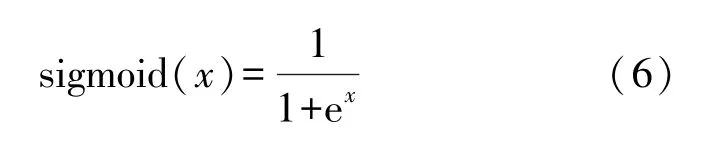
反向并联二极管伏安特性函数

diode(x)函数来源于反向并联二极管伏安特性函数

式中，u是二极管端电压，i(u)是流过二极管的电流，IS为二极管反向饱和电流，在常温下，kT/q=26 mV，工程实际中，二极管导通后电压基本不变，式(7)是反向并联二极管的伏安特性的近似公式，适用于在二极管导通电压“0.7 V”附近的伏安特性函数，式(8)的电流以指数显著变化，不宜直接作为蔡氏二极管的函数使用。将二极管伏安特性的导通“电压”归一化为以数字表达的“0.7”，反向并联二极管两端电流-电压关系即为式(7)，与式(1b)相比只是“0.7”和“1”差别，Chua L O 在文献[1-2]设计的蔡氏电路，转折点实际电压也不是“1”伏，受限于当时的技术，改变物理电路太难，默认为“1”伏，理论上，二极管实现的蔡氏电路与经典蔡氏电路是功能全同的。

式(4)、(5)与式(3)的特性曲线只是在波形上是相似的，函数只有数学意义，而式(7)具有工程背景和明确的物理意义；式(4)函数的物理硬件实现需要两个乘法器，式(5)函数在物理上用基本电子元件来实现目前还比较困难，式(7)函数只需两个二极管反向并联即可实现，十分简洁，在物理特性上与经典蔡氏二极管一样同属电压控制电流源(VCCS)器件；式(4)、(5)、(7)取代蔡氏二极管函数式(3)，是非线性单元的另外一种表达形式，所得方程与蔡氏电路是拓扑等效的。

2.3 三次型混沌系统动力学分析

在硬件电路实现之前，用虚拟仿真，获得定性认识，在混沌电路设计上是非常有必要的，式(4)、(5)、(7)替代非线性单元式(3)，得到3 类三次型函数蔡氏电路混沌系统，用MATLAB 仿真3 类系统，得到的x-y相图分别如图3 所示。

图3 3 类三次型蔡氏电路仿真的x-y 相图

混沌系统的Lyapunov 指数越大，系统运动越无序，动力学行为越复杂，对初值越敏感，有利于保密通信，针对设计的3 类三次型非线性函数，因为sgm(x)函数以指数变化，提高了系统的Lyapunov 指数，也符合理论实际，另外2 类减小了Lyapunov 指数，总体上差别不大，见表1。

表1 三次型蔡氏电路Lyapunov 指数

3 三次型蔡氏电路设计

所设计的三次型蔡氏电路均遵循原方程的主体结构和参数，考虑到电子元件标称值和实际值是有误差的，设计的电路原理图参数是允许有误差的，范围相对较大，例如，图4 中电阻R11的理论阻值为667 Ω，实际选取阻值为650 Ω～680 Ω 均可，电路焊接时，挑选精度较高，接近原理图参数的元件，即可实现混沌电路。

三次方蔡氏电路:蔡氏电路中的核心具非线性部分电路，由式(4)三次方函数的电路代替，设计的图4混沌电路与原蔡氏电路是拓扑等效的，也是微分同胚的，乘法器增益为0.1 V/V。

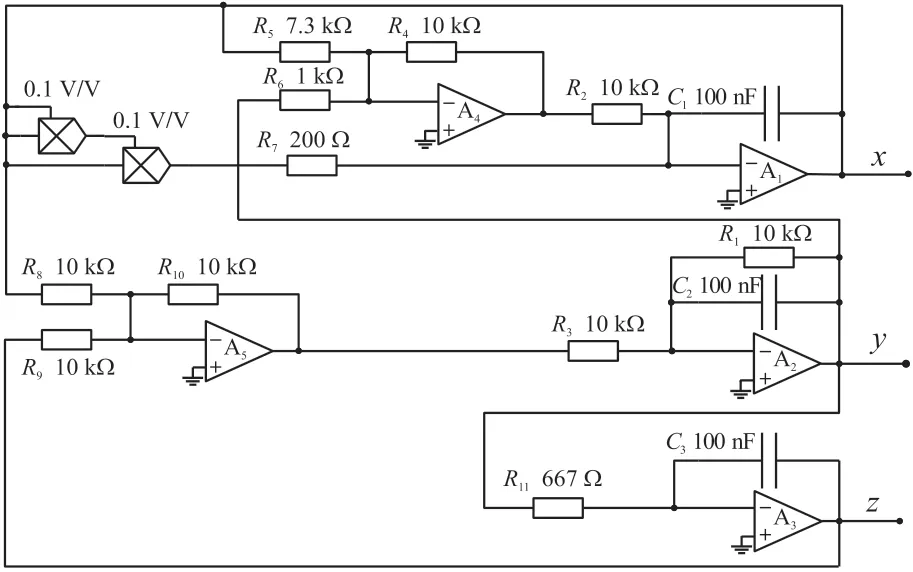
图4 三次方蔡氏电路原理图

二极管蔡氏电路1:电路原理图如图5 所示，利用二极管的钳位作用，反向并联二极管联接在串联电阻R7与电阻R5之间，实现式(7)函数的电路，直观，元件少，理论计算也容易，电路精度高，该反向并联二极管实现的输入输出是电压-电压的转换关系，与式(7)表达式相同，物理量有所区别。

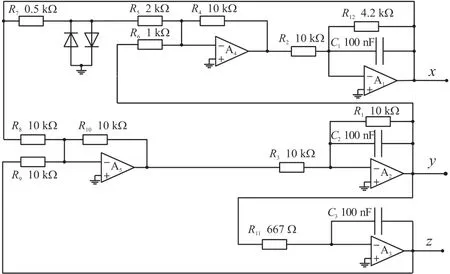
图5 二极管蔡氏电路原理图1

二极管蔡氏电路2:图6 中，反向并联二极管和电阻R9串联，理想二极管的导通电阻是为0 Ω、截止为∞Ω，电阻R9=R10，R9、R10串联有分压功能，输出的信号接入集成运放A5 的同向端，该反向并联二极管的输入输出也是电压-电压的关系，如式(9a)或(9b)所示，是式(1b)核心部分的另外一种写法，具有死区特性，波形图如图7 所示。

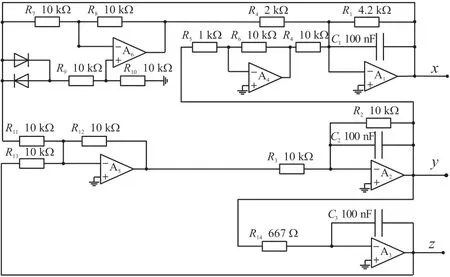
图6 二极管蔡氏电路原理图2

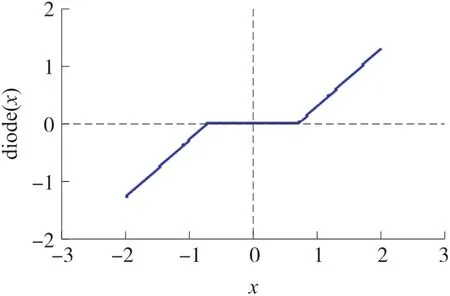
图7 并联二极管死区特性曲线

设计的如图5、6 所示的二极管蔡氏电路，与理论是有误差的，二极管反向不是完全截止的，二极管导通后电压也并非完全“0.7 V”不变，从工程方面来看实际影响很小，功能与蔡氏电路是全同的。

3 类三次型蔡氏电路物理实验相图如图8所示。

图8 三次型蔡氏电路物理电路x-y 相图

4 混沌保密通信电路设计

以本文提出的三次方蔡氏电路为例，采用反馈型驱动-响应式同步混沌保密通信制式[11]进行试验，电路原理图如图9 所示，由发送端、接收端和信道三部分组成，发送端输出信号为x1、y1、z1，接收端输出信号为x2、y2、z2，以x1信号为载波，调制信号为m，信道传输的是携带调制信息的混沌信号x′1，解调信号为保密精度高。

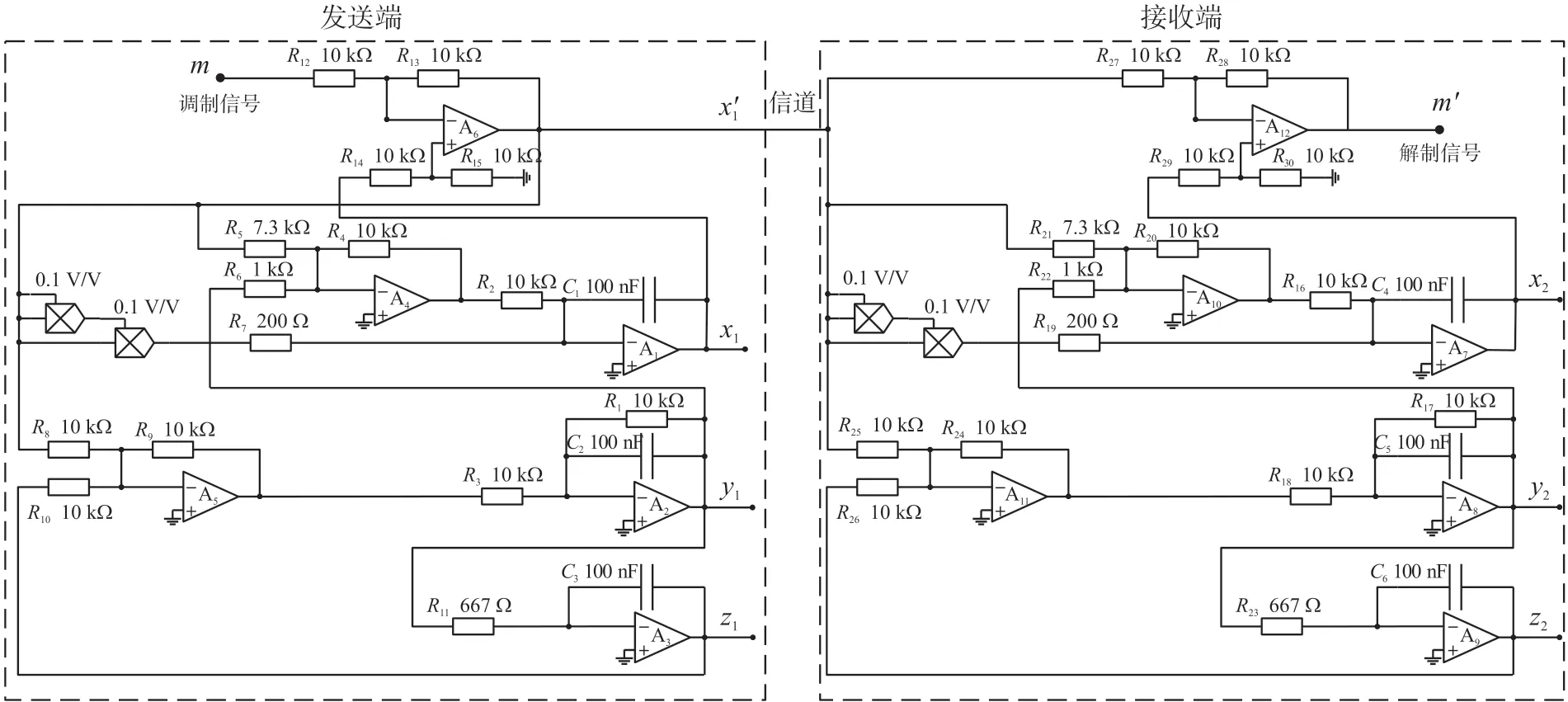
图9 三次方蔡氏电路混沌调制保密通信原理图

只要保密通信系统的收、发电路对应元件的参数相同，就可以达到设计的实验效果。图10(a)、(b)、(c)是物理电路实验时，示波器显示的收、发端同步时x1-x2，y1-y2，z1-z2的相图，同步得很好。

图10 混沌调制保密通信收、发端同步相图

图11(a)是将10 mV 的正弦调制信号m加入保密电路时，输出的x1-y1相图，依然是双涡卷混沌；图11(b)是系统携带加密信号m时的发送端x1波形图，接收端x2波形图，观察不到二者的差别；图11(c)是调制信号波形图与解调信号波形图，完全一致。此外，蔡氏电路的状态变量以电压形式输出，单位是伏特，调制信号是毫伏级，因此该保密通信电路噪声系数小于10-3，保密系统可靠。

图11 调制解调过程波形图

5 结语

1983 年Chua L O 提出的经典蔡氏电路，是混沌电路工程的典范，具有里程碑意义，非线性单元为核心部分，属于三次型函数，是分段线性的三折曲线，为后续分段线性混沌系统带来许多启示[12]。

(1)本文针对非线性单元的核心部分，在遵循蔡氏电路结构和参数的前提下，提出3 类三次型函数，设计了3 类蔡氏电路，均易于搭建实际混沌电路。

(2)本文提出的三次型蔡氏电路，是全同或者拓扑等效的蔡氏电路，方程简练，分析方便。

(3)本文提出的三次型蔡氏电路，适合于混沌保密通信，尤以主从式反馈型驱动-响应式混沌调制保密通信为优。