渐开线齿轮修形的分析计算

赵恒

（太原重工齿轮传动分公司， 山西 太原 030024）

试（实）验研究

渐开线齿轮修形的分析计算

赵恒

（太原重工齿轮传动分公司， 山西 太原 030024）

通过对国内外修形结果研究分析，阐述了齿轮修形计算的理论、方法以及具体的计算过程。通过齿顶修缘可使齿面载荷均匀分布，从而有效提高了齿面接触强度，改善了齿轮啮合性能，因此齿轮修形在实际生产中具有重要意义。

齿轮 修形 啮合线

齿轮修形是现代齿轮制造技术特点之一，是弥补齿轮由于加工误差及工作变形而引起的冲击、偏载等不利因素的重要手段。常见的齿轮修形有齿廓修形和齿向修形。齿廓修形又以齿顶修缘为主。在传统修形方法中，对于齿顶修缘高度的计算，是根据齿轮啮合时弹性变形规律，结合生产加工经验，取hc=0.4 mn（mm）来做为齿顶修缘的高度值。这个方法虽然计算简便，对齿轮啮合性能有一定的提高，但是这种计算方法只考虑了模数对修形量的影响，计算结果不够准确，并不适用于高速、高精度、重载的传动系统中。

1 修缘高度的分析计算

基于齿轮基圆端面节距的修缘高度计算，是通过对齿轮啮合过程分析，计算出实际工作啮合线的长度，然后将修形后的啮合线长度与基圆端面节距相比，使二者相等，进而求解处修缘高度。

通过对国内外修形结果分析发现，对齿顶修缘的齿轮都明确标注啮合线工作段长度（gFf）和齿顶修缘部分反映在啮合线上的长度（gRa），对齿顶修缘高度的计算思路也是一致的，即保证齿顶修缘后啮合线长度（见图1中l0）等于或稍大于端面基圆节距。不同之处在于对共轭齿轮，主、从动齿轮齿顶修缘啮合线长度（gRa1，gRa2）分配存在差异。

归纳起来，齿顶修缘高度计算方法如下：1）求啮合线工作段长度gFf。2）“修缘后齿廓”啮合线长度lo=Pbt。

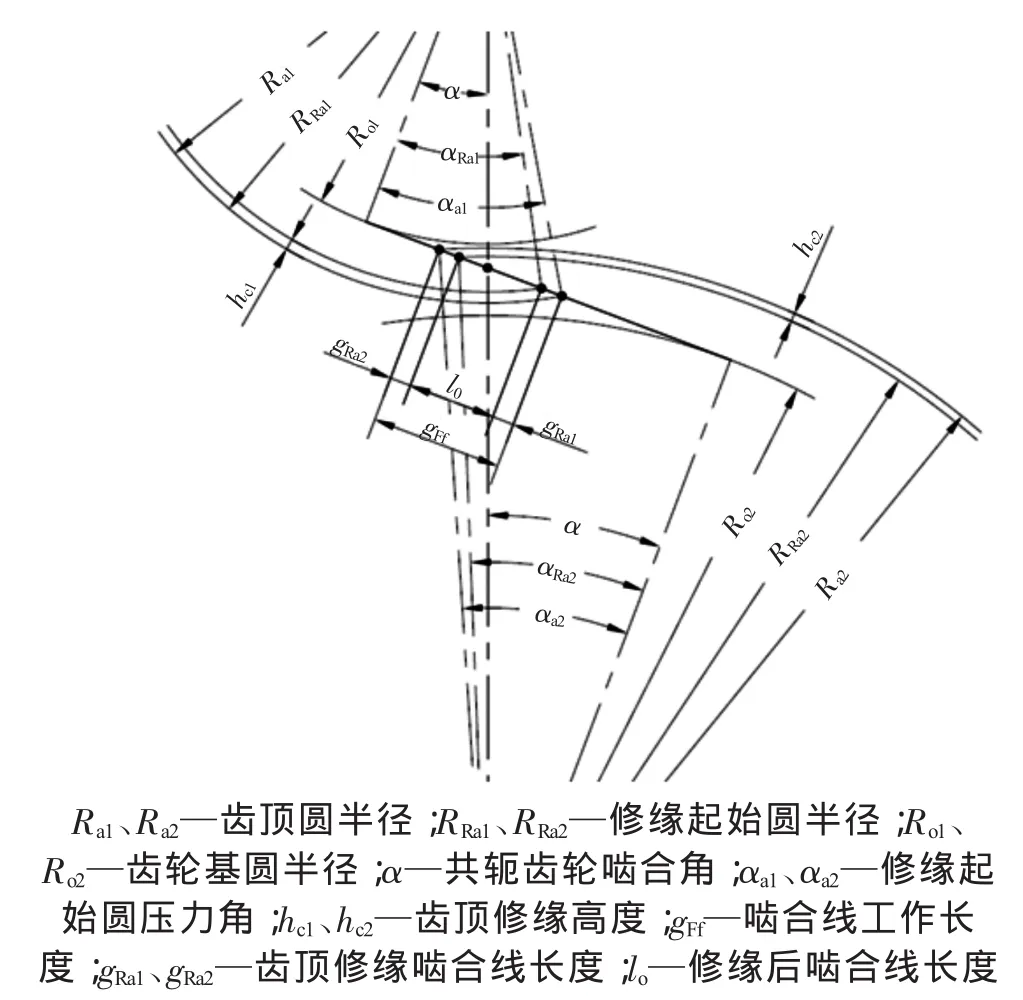
图1 外啮合齿轮传动

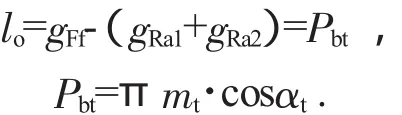
式中：Pbt为基圆齿距；mt为端面模数；αt为端面压力角。

3）对共轭齿轮齿顶修缘啮合线长度分配，目前常用的分配方式有三种。

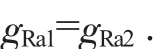
此种分配方式是按照共轭齿轮齿顶修缘啮合线长度相等来分配，计算过程简单，常规工况传动系统修形可采用此种方式。

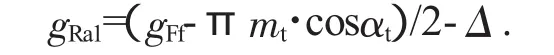
式中：Δ为齿顶、齿根修缘公差。其根据模数m不同，取值不同，范围为0.7～1.5。

此种分配模式中从动齿轮齿顶修缘啮合线长度大于主动齿轮齿顶修缘啮合线长度。

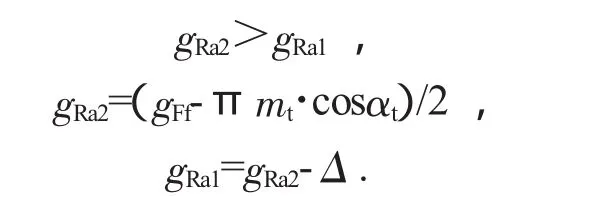
式中：Δ根据模数不同，其范围为0～0.5。当采用此分配方式时，应给予gRa1、gRa2二者一定的公差值，公差值根据模数值确定，范围为-2.4～-0.8。

此分配模式保证了“修缘后啮合线长度”大于基圆端面节距，即重叠系数ε大于1

4）求齿顶修缘起始圆压力角。

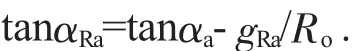
5）求修缘起始圆半径。

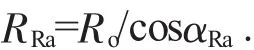
6）求齿顶修缘高度。

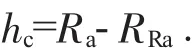
通过上述计算可以看出，齿廓修缘啮合线长度（gRa）并不是齿顶修缘高度（hc），而是修缘高度在啮合线上的反映，在进行磨齿修形时应注意二者区别。具体区别如图2所示。

图2 修形图

2 实例计算

齿轮参数见表1。

基本计算：

表1 齿轮参数

齿顶圆半径计算：

基圆半径计算：

啮合线工作长度计算:

则αa1=29.098°。

同理αa2=28.382°。

修缘啮合线长度计算：

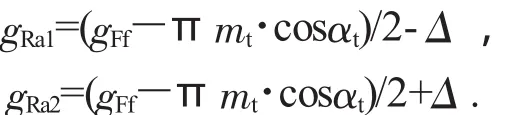
根据mn=25，取Δ=0.7，求得：

齿顶修缘起始圆半径计算：

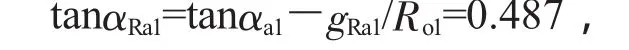
则αRa1=25.98°，

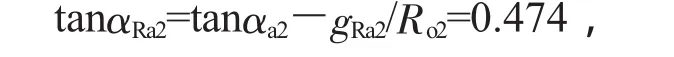
则αRa2=25.363°，

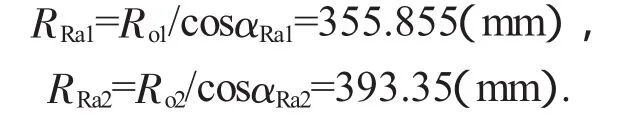
修缘高度计算：

3 结语

此种计算方法与传统的相比，结果更为准确，并可避免由于修形量过大导致修形后重叠系数小于1的情况的发生。因此广泛应用于风电、冶金、矿山等领域。

（编辑：苗运平）

Analysis and Calculation of Involute Gear Modification

ZHAO Heng
（Taiyuan Heavy Industry Gear Transmission Branch Co.,Taiyuan Shanxi 030024）

Through the research and analysis of modification results at home and abroad,the theory,method and concrete calculation process of gear modification calculation are expounded.Through the trimming of the top of the tooth,the load distribution of the tooth surface can be evenly distributed,so that the contact strength of tooth surface can be effectively improved,and meshing performance of the gear can be improved.Therefore,gear modification has important significance in actual production.

gear,modification,meshing line

TH132.414

A

1672-1152（2017）03-0013-02

10.16525/j.cnki.cn14-1167/tf.2017.03.05

2017-03-25

赵恒（1989—），男，山西临汾人，毕业于大连理工大学，学士学位，助理工程师。现就职于太原重工齿轮传动分公司，研究方向为齿轮传动设计。